基于自適應多重歐氏距離變換的分水嶺粘連顆粒分割方法

王增碩 劉溢文 關子昂 張哲 張壯壯

摘要：顆粒形狀以及顆粒粘連程度是影響粘連顆粒分割效果的主要因素，現(xiàn)有粘連顆粒分割方法主要存在兩方面不足：一些方法只能應對某一特定形狀顆粒的分割問題;大多數(shù)方法不能根據(jù)顆粒粘連程度自適應地調(diào)整分割算法，當粘連程度較大時容易出現(xiàn)欠分割。針對上述問題，該文提出了一種不限定顆粒形狀的自適應粘連顆粒圖像分割方法，該方法根據(jù)顆粒粘連程度對圖像進行自適應多重歐氏距離變換，得出分水嶺脊線對粘連顆粒圖像進行分割。實驗表明，本算法對不同形狀、不同粘連程度的顆粒均具有較好的分割效果。

關鍵詞：粘連顆粒;圖像分割;多重歐氏距離變換;自適應;分水嶺變換

中圖分類號：TP391? ? ? 文獻標識碼：A

文章編號：1009-3044（2022）03-0093-04

開放科學（資源服務）標識碼（OSID）：

引言

顆粒圖像的分割在工業(yè)生產(chǎn)、作物選種、醫(yī)療診斷、病理研究等領域都有著廣泛的應用[1-10]。然而在顆粒圖像中相鄰顆粒之間常常會出現(xiàn)不同程度的粘連或者重疊的現(xiàn)象，給圖像分割帶來挑戰(zhàn)。對粘連顆粒的準確分割是進一步分析、理解圖像內(nèi)容的前提，近年來吸引了廣大學者的競相研究。

現(xiàn)有的一些粘連顆粒圖像分割方法只能應對某一特定形狀的粘連顆粒，例如文獻[11-12]采用的橢圓擬合法針對橢圓形狀顆粒具有較好的分割效果，但對其他形狀的粘連顆粒分割效果較差;文獻[13-14]采用的基于形態(tài)學操作的迭代侵蝕方法僅對細胞這種類圓形顆粒在粘連邊界長度小于顆粒寬度的情況下具有較好的分割效果;文獻[15]針對棒材橫截面識別的問題，以標記分水嶺分割方法為基礎，引入距離變換與梯度重構的思想對其進行改進，而改進后的算法同樣僅對類圓目標具有較好的分割效果。

上述方法由于只適用于某一類特定形狀的顆粒，適用范圍有限。為了提高粘連顆粒分割算法對不同形狀顆粒的適用性，一些學者提出了不限定顆粒形狀的圖像分割方法。文獻[5]針對病斑粘連重疊問題，在分水嶺分割方法的基礎上采用最小二乘圓法誤差理論，提出了一種H-minima分水嶺分割方法，該方法對形狀多變且不規(guī)則的病斑分割效果好，但在粘連較大時仍會出現(xiàn)欠分割。文獻[6]針對重疊細胞圖像，利用距離變換以及斜率差分布閾值選擇的方法標記出粘連顆粒邊界上的瓶頸點，根據(jù)凹部原理確定粘連細胞分割線，此方法對多種不同形狀的顆粒都具有較好的分割效果，但是在粘連顆粒較多、粘連面積較大時會出現(xiàn)欠分割，分割效果較差。上述方法雖然對顆粒形狀的適用范圍較廣，但不能依據(jù)顆粒粘連程度靈活地調(diào)整分割策略，當粘連程度較大時容易出現(xiàn)欠分割。

本文提出一種基于自適應多重歐氏距離變換的分水嶺分割方法。該方法根據(jù)顆粒粘連程度，自適應地確定歐氏距離變換的最佳次數(shù)，通過分水嶺變換生成能夠劃分各個顆粒的分水嶺脊線，實現(xiàn)圖像中粘連顆粒的分割。實驗表明，所提方法對不同粘連程度的顆粒圖像均有較好的分割效果。

1分水嶺變換

分水嶺變換[16]是一種基于拓撲理論的數(shù)學形態(tài)學圖像分割方法。將灰度圖像視作地形地貌圖，圖像中每個像素的灰度值表示該位置處的海拔高度，每個局部極小值鄰域表示一個集水盆，相鄰集水盆的邊界稱為分水嶺，即用于分割粘連顆粒的分水嶺脊線。

分水嶺變換是一個迭代標注過程[17]。對于灰度圖像[I]，其最大灰度值和最小灰度值分別為[hmax]和[hmin]，[Th（I）]為[I]中灰度值小于或等于[h]的像素所構成的集合，[minh（I）]為[I]中灰度值等于[h]且屬于集水盆區(qū)域的像素所構成的集合。[dA（x，y）]為測地線距離，是區(qū)域[A]中兩個像素點[x]和[y]之間的最短路徑長度，且該路徑中的任一點都在區(qū)域[A]中。假設[A]包含一個由若干個連通分量[Bi]組成的集合[B]，那么[izA（Bi）]為[B]的連通分量[Bi]在[A]中產(chǎn)生的測地線影響區(qū)，該區(qū)域由[A]中到[Bi]的測地線距離小于到[B]其他任何連通分量的測地線距離的像素點構成。[A]區(qū)域中到相鄰兩個連通分量[Bi]和[Bj]測地線距離相同的像素點就構成了集合[B]在[A]內(nèi)不同測地線影響區(qū)的邊界，該邊界可用于分割粘連顆粒，也稱為分水嶺脊線。分水嶺變換方法生成分水嶺脊線的迭代方式為[13]：

[Xhmin=Thmin（I）Xh+1=minh+1?IZTh+1（I）（Xh）]? ? ? ? ? ? ? ? ? ? ? （1）

式（1）中，[?h∈[hmin，hmax-1]]。灰度值[h]從[hmin]逐漸增加到[hmax-1]，[Xh]隨之發(fā)生變化，而分水嶺脊線的建立就是[Xhmax]中不同測地線影響區(qū)邊界形成的過程。迭代計算完成后，取[Xhmax]區(qū)域對應的補集即可得到灰度圖像[I]的分水嶺脊線。

2基于歐氏距離變換的分水嶺分割方法

傳統(tǒng)的分水嶺算法對灰度圖像的梯度圖進行分水嶺變換得到粘連顆粒分割線，當顆粒灰度不均勻時，容易產(chǎn)生過分割。基于歐氏距離變換的分水嶺分割方法對二值圖像的歐氏距離變換圖進行分水嶺變換[18]，這種方法不使用原圖像的灰度信息，避免了過分割現(xiàn)象的出現(xiàn)，并且能夠最大限度地保證顆粒邊緣信息的完整性。其具體實現(xiàn)過程如圖1所示：

歐氏距離變換通過計算二值圖像中每個像素點到最近非零值像素點的歐氏距離，并以此作為該像素點對應位置上的灰度值，得到能夠描述二值圖像中顆粒分布情況的歐氏距離變換圖[19]。

在二值圖像[bw]中，記顆粒區(qū)域[Q]中的像素值為1，背景區(qū)域[B]中的像素值為0，則[bw]中像素[（xi，yi）]的歐氏距離變換為：

[dE（xi，yi）=min（（xi-sj）2+（yi-tj）2）]? ? ? ? ? ? ?（2）

式（2）中，[（sj，tj）∈Q]，[dE]為歐氏距離變換圖。

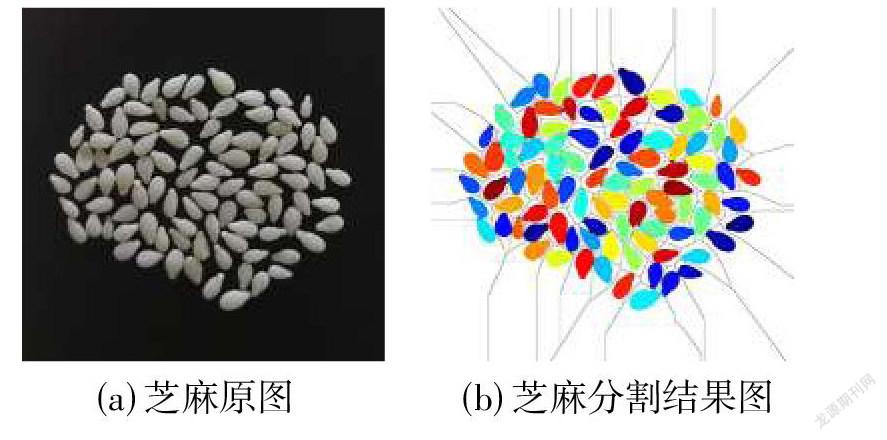
圖2以芝麻圖像（圖2（a））為例，展示了基于歐氏距離變換的分水嶺分割方法的實現(xiàn)過程。根據(jù)分割結果（圖2（f）），位于左上方的兩個粘連芝麻顆粒沒有被分割開，原因在于這兩個芝麻顆粒在進行一次歐氏距離變換后依然存在明顯的連通關系（將圖2（d）取反可便于觀察，如圖3所示），因此在后續(xù)分水嶺變換的過程中沒有生成能夠分割兩個粘連芝麻顆粒的分水嶺脊線，出現(xiàn)欠分割。

3基于自適應多重歐氏距離變換的分水嶺分割方法

對粘連顆粒采用歐氏距離變換可以有效地將粘連處的連接程度降低[20]。僅進行一次歐氏距離變換容易在顆粒粘連程度較大時無法斷開粘連處的連接，在后續(xù)的分水嶺變換中無法獲得理想的分水嶺脊線，導致欠分割。通過增加歐氏距離變換的次數(shù)可有效解決上述欠分割問題。然而一味地增加歐氏距離變換次數(shù)容易造成過分割，為了解決這一問題，本文提出一種自適應多種歐氏距離變換的方法，根據(jù)圖像中顆粒的具體粘連程度，自適應地確定歐氏距離變換的最佳次數(shù)，實現(xiàn)對不同程度粘連顆粒的有效分割。

自適應多重歐氏距離變換的具體實現(xiàn)過程如下：

（1） 對二值圖像作一次歐氏距離變換，并進行分水嶺變換得到分水嶺脊線圖;

（2） 使用分水嶺脊線分割粘連顆粒，并計算分割結果中所有連通域面積[Si]的均值[μ]和標準差[σ]。

[μ=1ni=1nSi]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（3）

[σ=i=1n（Si-μ）2n]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （4）

上式中，[n]為連通域的個數(shù);

（3） 利用“[+2σ]準則”進行自適應判斷，計算

[P=i=1n（max（0，Si-（μ+2σ）））]? ? ? ? ? ? ? ? ? ?（5）

若[P>0]，則[Si]中存在大于[μ+2σ]的連通域面積，分割結果中依然存在粘連顆粒，將歐氏距離變換圖在取反和二值化后再次進行歐氏距離變換，重復上述過程，直到[P=0];

（4） 繼續(xù)做兩次歐氏距離變換，對得到的歐氏距離變換圖進行分水嶺變換，取出分水嶺脊線分割粘連顆粒，并與步驟（3）中[P=0]對應的分割結果進行比較，若連通域數(shù)量有增加則[P=0]對應的分割結果中依然存在粘連顆粒，轉到步驟（2），若沒有增加則[P=0]對應的分割結果中不存在粘連顆粒，將其視作本算法最終的分割結果。

同樣以圖2（a）為例，基于自適應多重歐氏距離變換的分水嶺分割結果如圖4所示：

根據(jù)圖4的分割結果，本算法能夠根據(jù)顆粒粘連程度自適應地調(diào)整歐氏距離變換的次數(shù)，使得算法在粘連程度較大的顆粒之間依然可以生成分水嶺脊線將粘連顆粒有效分割，解決了基于一次歐氏距離變換方法的欠分割問題。

4實驗與分析

為驗證本文算法對不同形狀顆粒的適用性以及對不同粘連程度顆粒的自適應分割能力，分別設計以下兩個實驗：（1） 不同形狀顆粒粘連圖像的分割實驗;（2） 本文算法與基于一次歐氏距離變換的分水嶺分割算法的對比實驗。

4.1不同形狀顆粒粘連圖像分割實驗

選取芝麻和大米兩種不同形狀的顆粒作為待分割對象，使用本文所提基于自適應多重歐氏距離變換的分水嶺分割方法，對兩種顆粒的粘連圖像進行處理。分割結果如圖5、圖6所示：

從以上分割結果中可以看出，本文提出的基于自適應多重歐氏距離變換的分水嶺分割方法對多種不同形狀顆粒的粘連圖像都具有較好的分割效果，并且保留了顆粒的完整邊緣信息，有利于后續(xù)粒徑測量和分析工作的進行。

4.2粘連顆粒分割方法對比實驗

以芝麻和大米的粘連顆粒圖像為待處理目標，分別使用本算法和基于一次歐氏距離變換的分水嶺分割算法對其進行處理，得到分割結果如圖7、圖8所示。

對比兩種算法的分割結果可以發(fā)現(xiàn)：基于一次歐氏距離變換的分水嶺分割算法在顆粒粘連程度較大、粘連數(shù)量較多時欠分割問題嚴重，而本算法能根據(jù)顆粒粘連程度與粘連數(shù)量自適應地調(diào)整歐氏距離變換次數(shù)，對粘連顆粒有效分割。

5結束語

本文提出的基于自適應多重歐氏距離變換的分水嶺粘連顆粒分割算法能夠依據(jù)顆粒粘連程度自適應地調(diào)整歐氏距離變換次數(shù)，可有效應對不同粘連程度的粘連顆粒圖像分割問題。并且，本方法對顆粒形狀沒有限定，可用于多種不同形狀的顆粒分割，適用范圍廣。

在后續(xù)的研究中，將進一步優(yōu)化本算法中的自適應判定準則，使之能夠靈活地應對更多不同形狀的顆粒以及更復雜的粘連情況。

參考文獻：

[1] 孫建平，楊亞男，齊園園.基于數(shù)字圖像處理的燃用煤矸石粒徑檢測[J].電力科學與工程，2013，29（3）：55-58.

[2] 匡芳君，徐蔚鴻，王艷華.基于改進分水嶺算法的粘連大米圖像分割[J].糧食與飼料工業(yè)，2010（8）：5-8.

[3] 陳家新，王紀剛.一種改進的醫(yī)學圖像分水嶺分割算法[J].計算機應用研究，2013，30（8）：2557-2560.

[4] 王婭.血液紅細胞圖像自適應標記分水嶺分割算法[J].中國圖象圖形學報，2017，22（12）：1779-1787.

[5] 張建華，韓書慶，翟治芬，等.改進自適應分水嶺方法分割棉花葉部粘連病斑[J].農(nóng)業(yè)工程學報，2018，34（24）：165-174.

[6] Wang Z Z.Bottleneck detection by slope difference distribution：a robust approach for separating overlapped cells[J]. arXiv preprint arXiv： 1912.05096， 2019.

[7] 蔣文娟，李富蕓，徐冬.基于模糊C均值聚類算法的腦部CT圖像分割[J].電腦知識與技術，2020，16（7）：197-198，200.

[8] 謝裕睿，徐偉恒，董建娥.基于圖像處理的植物病斑分割方法研究[J].電腦知識與技術，2020，16（3）：216-217.

[9] 韓殿元，王國穎.基于HSV色彩空間的OTSU色素障礙性皮膚病圖像分割[J].電腦知識與技術，2019，15（33）：213-214.

[10] 石林立，徐鋒，王攀.基于分形維數(shù)的風機表面損傷圖像分割[J].電腦知識與技術，2020，16（6）：191-194.

[11] Bai X Z，Sun C M，Zhou F G.Splitting touching cells based on concave points and ellipse fitting[J].Pattern Recognition，2009，42（11）：2434-2446.

[12] Brüllmann D D，Pabst A，Lehmann K M，et al.Counting touching cell nuclei using fast ellipse detection to assess in vitro cell characteristics：a feasibility study[J].Clinical Oral Investigations，2012，16（1）：33-38.

[13] Wang Z Z.A new approach for segmentation and quantification of cells or nanoparticles[J].IEEE Transactions on Industrial Informatics，2016，12（3）：962-971.

[14] Wang Z Z，Yin L J，Wang Z H.A new approach for cell detection and tracking[J].IEEE Access，2019，7：99889-99899.

[15] 劉國華，李濤.基于改進的標記分水嶺方法的棒材識別[J].光電子·激光，2019，30（2）：160-167.

[16] 徐奕奕，劉智琦，劉琦.基于改進的分水嶺算法圖像分割方法研究[J].計算機仿真，2011，28（9）：272-274.

[17] Vincent L，Soille P.Watersheds in digital spaces：an efficient algorithm based on immersion simulations[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1991，13（6）：583-598.

[18] 黃明鑫，楊龍興，莊立東，等.基于HALCON圖像處理的粘連零件顆粒計數(shù)方法研究[J].機械設計與制造工程，2016，45（2）：85-89.

[19] Wang J L，He J L，Han Y，et al.An Adaptive Thresholding algorithm of field leaf image[J].Computers and Electronics in Agriculture，2013，96：23-39.

[20] 秦襄培，鄭賢中.MATLAB圖像處理寶典[M].北京：電子工業(yè)出版社，2011.

【通聯(lián)編輯：唐一東】