模仿、遷移、創新：數學建模教學的三重進階

【摘 要】數學建模是指用數學知識解決生活問題，需要學生能用數學的眼光將生活問題抽象成數學模型，并用數學思想方法解決模型，最終用數學語言表達、解釋生活問題。在數學教學中，教師可以依據學情，指導學生經歷模仿、遷移到創新三重進階，幫助學生提高數學建模能力、提高數學素養。

【關鍵詞】數學建模；模仿；遷移；創新

【中圖分類號】G633.6? 【文獻標志碼】A? 【文章編號】1005-6009（2022）91-0039-03

【作者簡介】張陽，江蘇省蘇州市吳江區教育局教研室（江蘇蘇州，215200）教研員，高級教師。

數學源于對現實世界的抽象，基于抽象結構，通過符號運算、形式推理、模型構建等，理解和表達現實世界中事物的本質、關系和規律。數學建模并非求解數學應用題，它需要用數學的眼光將生活問題抽象成數學模型，并用數學思想方法解決模型，最終用數學語言表達、解釋生活問題。

數學建模是學生學科素養與理性精神的綜合體現。教師需要指導學生經歷模仿、遷移到創新的三重進階，最終實現學生數學建模能力的素養化、自覺化。

一、模仿：進入數學建模世界

模仿是教與學的基本方法，有著極其豐富的內涵，主要體現在以下三個方面：一是指人類本能的模仿，二是有明確目的的模仿，三是以創新為目標的模仿。數學建模教學中的模仿，主要是指導學生模仿教師的解題過程，學習數學建模思想方法，體驗數學建模過程，進入數學建模世界。

數學建模中的模仿可以分為三個環節：一是教師示范數學建模過程，二是學生模仿數學建模，三是以學生為主提煉建模步驟，形成建模方法。

1.課例展示

【例1】 測量操場上旗桿的高度：（1）成立測量小組；（2）研究測量目標和測量方法；（3）制訂兩套測量方案（含測量精度）；（4）明確小組成員的任務分工；（5）實施現場測量，記錄并處理測量數據；（6）小組內交流填寫《測量工作報告表》；（7）班級成果交流。

教師示范方案1，構造平面三角形。隨后安排學生分組討論。學生給出方案2、方案3及方案4。（見圖1）

“測量旗桿高度”本質是用數學的眼光觀察世界，用數學知識抽象現實問題，體現了數學建模的思想，用到的數學學科知識有三角函數、解三角形。4種方案中，方案1構造平面三角模型，方案2構造等腰直角三角形模型，方案3構造立體模型，方案4構造平面幾何模型。方案1與方案2對測量條件要求較高，方案3與方案4可以測量處于較為復雜環境的物體的高度。

2.關于模仿的思考

從教育學的角度來說，“知行合一”是模仿的理論依據，教學所達成的能力與素養是隱性的，不可以直觀呈現。在教學中教師能夠傳授可見的定義、定理，可言述的方法、技巧，還有不可言傳的思想感悟等。學生只有在模仿中進行體驗實踐，才有可能形成具有個性化的能力素養。

在開展教學活動時，教師應注意以下四個方面。第一，模仿的提煉環節是對數學建模的升華，是由特殊到一般的內化過程，需要通過圖表等形式輔助理解抽象意義。第二，教師示范指在教師的指導下學生進行建模活動。在此過程中，教師應保證建模活動的進度、質量與安全。第三，模仿活動與建模活動在形態上相似度越高，模仿活動的難度就越低，需要教師依據學情合理設計作業。第四，模仿在教學中占有的比例需要根據教學內容與學生認知水平共同決定。

二、遷移：形成數學建模能力

遷移是指一種學習對另一種學習產生的影響。現代遷移理論主要有三種，一是心理學角度的結構遷移理論，探討人的內部因素對遷移的影響；二是知識角度的建構主義遷移理論，認為知識結構越完善，學習遷移的能力越強；三是教育學角度的類比遷移理論，認為學習是利用已經掌握的問題解決方法去解決新問題。以上理論有兩個共同觀點，一是認知結構水平在遷移中處于核心地位，二是外部環境和主體相互作用對遷移具有重要影響。

1.課例展示

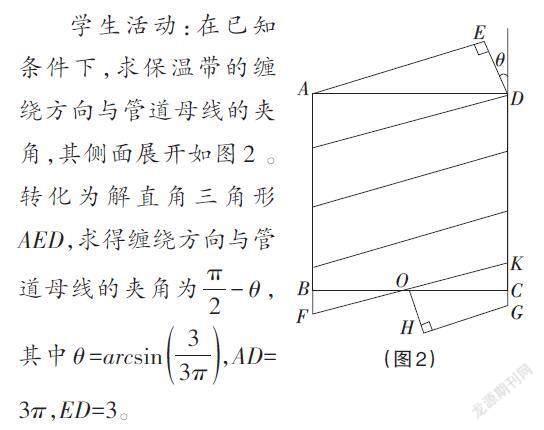
【例2】 防止水管凍裂，需用保溫帶纏繞在管道外部。若管道的直徑為3cm，保溫帶寬度為3cm，為節省材料，如何進行包扎才能使保溫帶全部包住管道且不重疊。

學生活動：在已知條件下，求保溫帶的纏繞方向與管道母線的夾角，其側面展開如圖2 。轉化為解直角三角形[AED]，求得纏繞方向與管道母線的夾角為[π2] - θ ，其中θ =arcsin [33π]，AD=3π，ED=3。

將現實問題抽象為數學模型，需要數據收集與處理、數學抽象、邏輯推理、數學運算等學科素養。

2.關于遷移的思考

數學模型選擇是遷移質量的關鍵。一個好的數學模型需要有三個條件，一是有較強的實際背景，有利于培養學生用數學的眼光觀察身邊的生活模型；二是數學模型結果與實際問題結果相近，具有可實踐性；三是數學模型需要經歷多次修改、不斷完善。例2中還有許多地方值得商榷改進，如保溫帶有一定的彈性，這種彈性很難控制。

對于數學建模能力的遷移評價可以從四個維度進行：一是敏感程度，即學生對生活中的現象能否主動用數學的眼光進行觀察；二是知識維度，即學生對于生活問題的抽象過程能否自覺聯結到相關數學知識；三是技能維度，即學生在建模過程中能否選擇最優方案；四是反思維度，即學生能否對建模過程進行反思、改進，探尋建模中的不足。

三、創新：實現數學建模自覺

數學建模自覺是學習發展到一定程度后的必然結果，它的養成需要學生具有系統的學科知識儲備、理性精神、批判性思維和良好的隱性知識。自覺數學建模的直接表現是理性思維，是在對照已有知識的基礎上，提出新的概念、觀點、方法，是對原有知識的一種增值活動。創新環節可以分為三個階段：研究問題、提出新穎觀點、分析論證。

【例3】請同學們閱讀這樣一條短信。“尊敬的客戶：您的戶號12053900000于2022年4月產生水費80.25元，用量25噸。請盡快繳納。如逾期未繳，我司將于2022年5月20日開始按日收取水費違約金。

師：這段文字是吳江水務公司發給用戶的短信，請同學們提取短信中涉及的數學問題。

生：水費與用水量之間是什么關系？繳納時間與繳納費用間的數學關系如何表達？

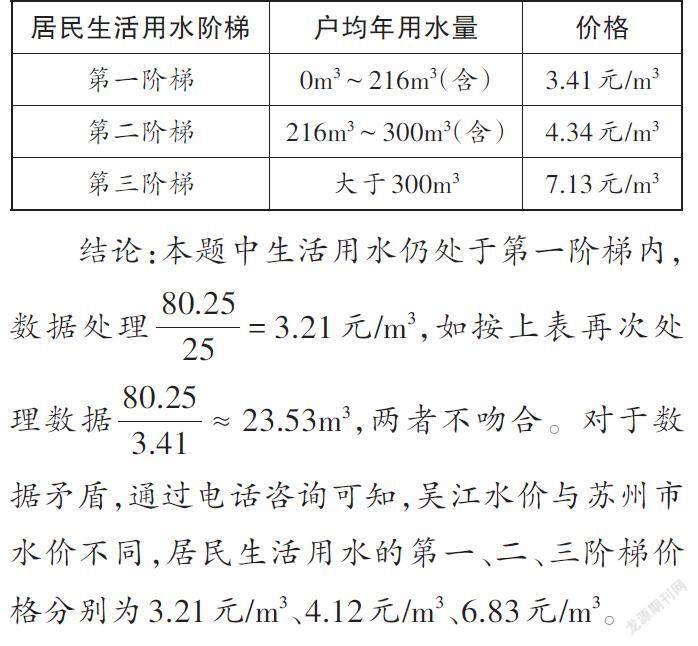
師：非常好，現在我們選取問題“水費與用水量之間的關系”作為研究對象，探究吳江地區水費與用水量間的函數關系式。從例3中的文字信息提煉出的數學信息無法形成完整的函數關系，我們上網查詢蘇州市居民用水價格表如下。

[居民生活用水階梯 戶均年用水量 價格 第一階梯 0m3～216m3（含） 3.41元/m3 第二階梯 216m3～300m3（含） 4.34元/m3 第三階梯 大于300m3 7.13元/m3 ]

結論：本題中生活用水仍處于第一階梯內，數據處理[80.2525] = 3.21元/m3，如按上表再次處理數據[80.253.41≈23.53]m3，兩者不吻合。對于數據矛盾，通過電話咨詢可知，吳江水價與蘇州市水價不同，居民生活用水的第一、二、三階梯價格分別為3.21元/m3、4.12元/m3、6.83元/m3。

2.關于創新的思考

依據創新的概念與特征，數學建模需要在現實生活中發現問題，建構數學模型，求解數學模型中的問題，最后解釋問題。創新需要良好的學科素養。數學學科素養有兩個層次，一是在學科問題的背景下，應用知識解決學科問題，如常見的數學應用題；二是現實問題的解決中，自覺應用學科知識解決問題，如例3的水費問題。

學生數學素養的形成是一個漸進過程，數學建模素養的培養同樣遵循這一規律，需要經歷模仿、遷移、創新三重進階，教師在數學教學中可以依據學情與學生的認知規律，選取對應策略組織教學，幫助學生形成數學建模能力，實現素養培育。