概周期驅動的二維分段線性范式系統的奇異非混沌吸引子

徐 震，沈云柱

(濟南大學 數學科學學院，山東 濟南 250022)

奇異非混沌吸引子(SNAs)是在幾何上表現為奇異，但最大李雅普諾夫指數非正且不具備對初值條件的敏感性的吸引子。1984年Grebogi等[1]發現在某些動力系統中可能存在SNAs，并以連續時間非線性振蕩器為例，首次驗證了SNAs的存在。在過去幾十年中，學者們進行大量有關SNAs的實驗并取得了許多研究成果[2-8]，在各種動力系統中發現了不同類型的分岔，并研究這些分岔中的SNAs，例如霍普夫分岔[9]、邊界碰撞分岔[10-11]、擦邊分岔[12]和爆裂分岔[13]等。隨著電子科學的不斷發展，學者們探究了電子電路中的SNAs。Paul等[14]通過相空間分析、龐加萊界面和李雅普諾夫指數等，分析由2個正弦驅動的具有共同分段的非線性LCR(電感-電容-電阻)電路耗散振子組成模型中的SNAs，并運用實時電子電路為驗證系統中SNAs的存在性提供了實驗證據。張永祥等[15]研究了一種新的概周期驅動電路系統中多種類型的SNAs及其不同生成機理，結果表明，系統中存在一種新的由環面分岔形成的類似輪胎形或管道形的SNAs。謝帆等[16]利用電流反饋形降壓變換器(Buck變換器)，研究2個三段式分段光滑系統的邊界碰撞和分岔，得到了在離散模型中該系統關于邊界碰撞和分岔的理論。隨著SNAs在通信安全[17-18]、氣候變化[19]等領域中應用前景的不斷擴大，SNAs逐漸成為國際非線性動力學研究的重點之一。隨著近幾年光滑系統的SNAs理論的不斷完善，國內外學者們開始研究分段光滑(非光滑)系統的SNAs，并取得了許多成果[20-23]，但相應的理論還不夠完善，有待進一步研究和驗證。

本文中以概周期驅動二維分段線性范式系統為研究對象，探討系統中是否存在SNAs。首先通過相軌跡圖尋找奇異吸引子，并利用最大李雅普諾夫指數驗證奇異吸引子是否是混沌的；然后通過有理逼近加以驗證；最后利用功率譜、相敏感函數和回歸圖對吸引子進行進一步分析。

1 系統模型建立

二維分段線性范式模型[24]為

(1)

式中：n∈為系統的迭代次數；xn、yn分別為系統第n次迭代時的輸入、輸出變量；τm、τr、δm、δr為固定的系統參數；u為分岔參數。方程(1)加入概周期驅動力后變為

(2)

φn+1=mod(φn+ω, 1),

(3)

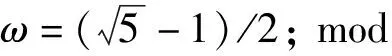
為了描述概周期驅動二維分段線性范式系統的SNAs，給出x軸方向上的最大李雅普諾夫指數λx的計算公式，即

(4)

式中xi為系統第i次迭代時的輸入變量。

2 系統的SNAs

SNAs的識別與檢驗過程如下。首先固定系統參數為τm=0.86，τr=-1.6，δm=0.3，δr=0.3，取激振動力幅值b=0.4，概周期驅動的二維分段線性范式系統在不同控制參數a時的相軌跡圖如圖1所示。由圖1(a)可知，當a=-0.094時，系統(2)中的吸引子是光滑的且系統圖像在相軌跡圖中表現為第1個周期內的概周期環面。由圖1(b)可知，當a=-0.023時，相軌跡圖中開始出現不連續點，光滑的概周期環面變為非光滑環面。由圖1(c)可知，當a=-0.022時，非光滑環面出現分形，通過計算可得，最大李雅普諾夫指數約為-0.102 9，此時吸引子為SNAs。由圖1(d)可知，當a=0.135時，奇異非混沌現象變得非常明顯，此時最大李雅普諾夫指數約為-0.032 6。當a>0.135時，系統開始進行混沌運動，進入混沌區域。

2.1 有理逼近

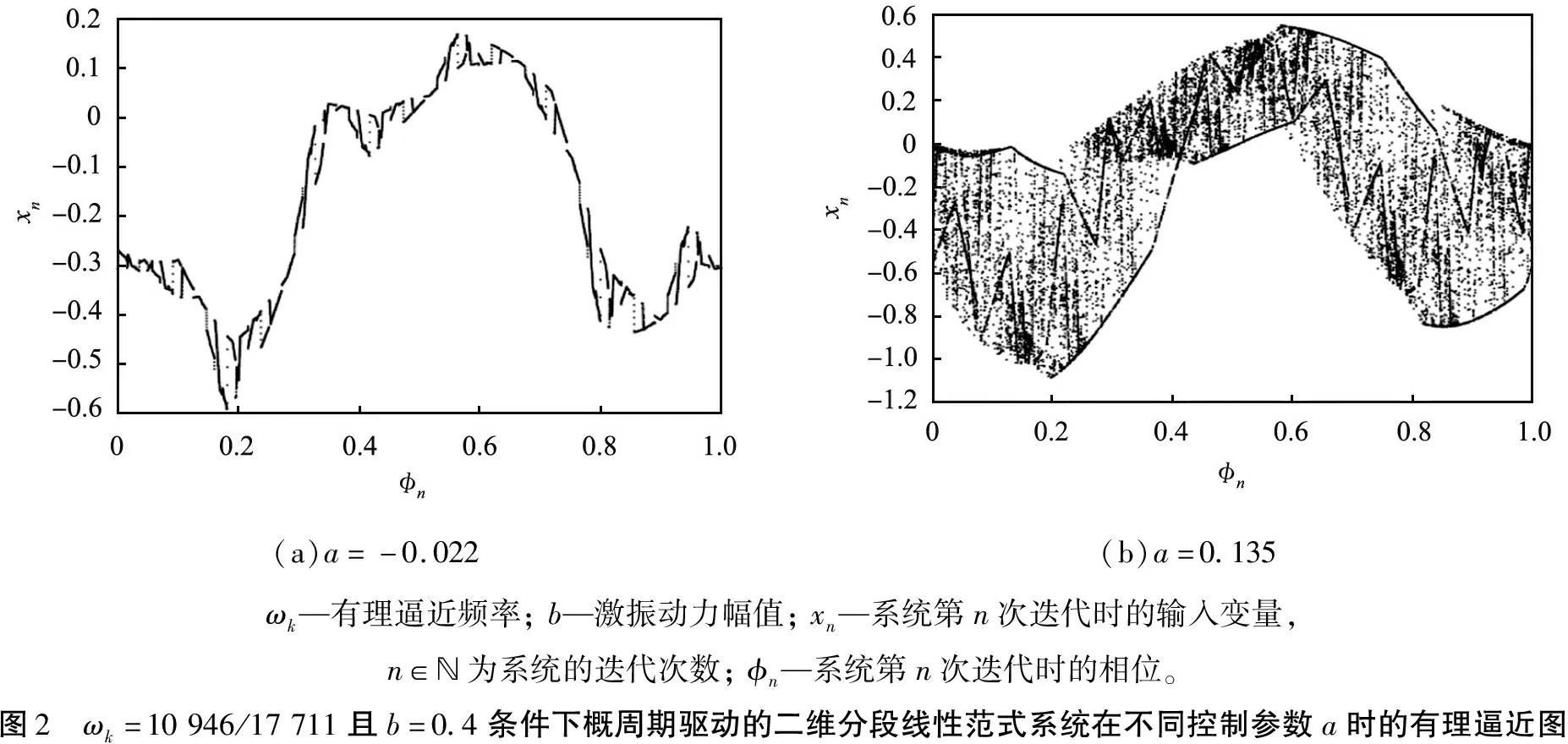
概周期驅動的二維分段線性范式系統的頻率ω為黃金分割值，運用Fibonacci數列的特性對ω進行有理逼近，得到有理逼近頻率ωk=Fk-1/Fk，k∈，Fk∈K，滿足Fk+1=Fk+Fk-1，K={1,1,2,3,5,8,13,21,…}。當k→∞時，系統的相軌跡圖出現SNAs。在ωk=10 946/17 711且激振動力幅值b=0.4的條件下，概周期驅動的二維分段線性范式系統在不同參數a時的有理逼近圖如圖2所示。對比圖2(a)、圖1(c)以及圖2(b)、圖1(d)可以發現，相同參數時的相軌跡圖與有理逼近圖具有相同的奇異特性，證明在參數a=-0.022，b=0.4和a=0.135，b=0.4時的吸引子為SNAs。

2.2 功率譜

功率譜是驗證吸引子是否為SNAs重要手段之一。SNAs的功率譜有奇異連續的特性，在功率譜圖像中表現為有許多自相似的峰，而周期吸引子不具備這種特性。

由傅里葉變換

(5)

得到功率譜為

(6)

式中：X(ωc,n)為傅里葉級數；ωc∈[0,1]為功率譜頻率；r為傅里葉變換的迭代次數；xr為系統第r次迭代時的輸入變量；|·|為模運算。

圖3所示為概周期驅動的二維分段線性范式系統在不同控制參數a時的環面功率譜。由圖3(a)可知，當a=-0.094時，光滑環面的功率譜沒有表現出奇異連續的特性。由圖3(b)可知，當a=0.135時，環面的功率譜既表現出奇異連續的特性，又具有很多自相似的峰，證明此時吸引子為SNAs。

(a)a=-0.094

2.3 相敏感函數

相敏感指數也是驗證吸引子是否為SNAs的重要手段之一。SNAs的相敏感函數Fn=nμ滿足冪律關系，μ為SNAs的相敏感指數。Fn隨著n的增大而無限增大。對于環面，相敏感函數則具有有界性。相敏感函數計算公式為

(7)

式中：x0為系統的初始輸入量；φ0為系統的初始相位；

(8)

其中φi為系統第i次迭代時的相位。

圖4所示為概周期驅動的二維分段線性范式系統在不同控制參數時的相敏感函數。從圖中可以看出，環面的相敏感函數表現出明顯的有界性，而與nμ滿足冪律關系的SNAs的相敏感函數則表現出無限增長趨勢，通過計算可得，SNAs的相敏感指數為μ≈0.475。

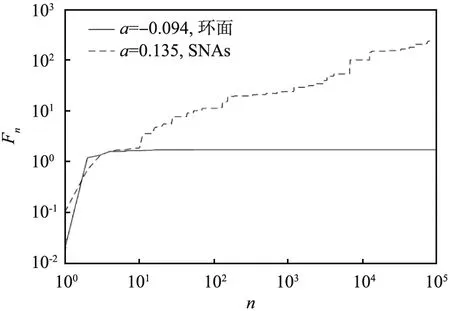
Fn—相敏感函數；n—系統的迭代次數，n∈；SNAs—奇異非混沌吸引子。

2.4 回歸圖

引入回歸圖可視化動態系統狀態反復出現的時間。利用遞推矩陣跟蹤不同的結構，可以區分下劃線軌跡的各種動力學狀態。通過觀察回歸圖可以明確系統在固定時間段上的狀態。回歸圖中的重現是系統的軌跡回到它曾經訪問的位置的時間，而回歸圖則是系統的軌跡在相同位置的時間對的集合。周期軌道的回歸圖將出現重復、連續的紋理，時間對產生倍數分隔并形成對角線。系統的回歸圖矩陣計算公式為

(9)

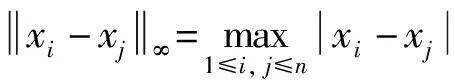
圖5所示為激振動力幅值b=0.4條件下概周期驅動的二維分段線性范式系統在不同控制參數a時的回歸圖。由圖5(a)可知，當a=-0.094時，回歸圖出現重復且不間斷的紋理，并且時間對會形成對角線紋理，證明吸引子位于概周期軌道上。由圖5(b)可知，當a=0.135時，回歸圖中出現大量的孤立點和一些較短的對角線，說明系統的重現過程是復雜的，證明吸引子為奇異吸引子，但是此時最大Lyapunov指數是負的，因此證明吸引子是SNAs。

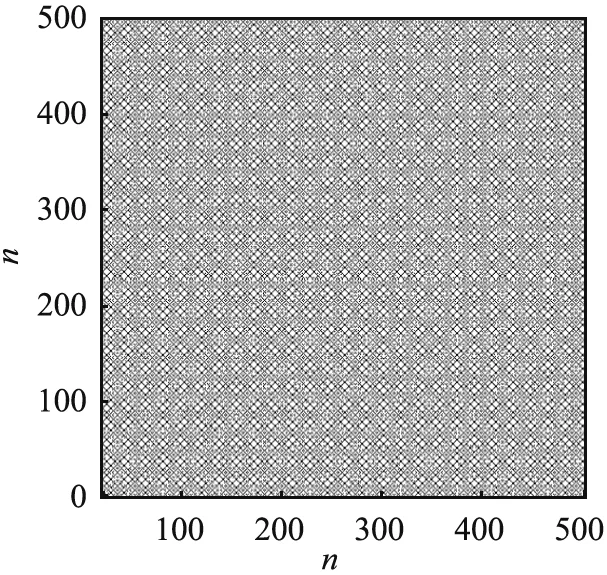
(a)a=-0.094

3 結語

本文中以一類概周期驅動分段線性范式系統為模型，研究系統中是否存在SNAs。通過觀察相軌跡圖并計算最大李雅普諾夫函數，發現了該系統中存在的SNAs，并運用有理逼近、功率譜和回歸圖，對系統中的SNAs進行了深入分析。研究結果表明，概周期驅動分段線性范式系統中存在SNAs。不同的概周期驅動系統中是否存在SNAs，存在的SNAs的類型是否相同，還有待進一步研究。