掛衣架問題的前世今生

李 鑫

(浙江省桐鄉第一中學)

受力分析是高中物理的重難點，有各種各樣的定式，比如掛衣架模型.基于經典模型的演化和拓展是高三復習的一個重要方向.本文先從掛衣架經典問題出發，依次涉及各種變式，并探討變式背后的深刻物理原理.

例1如圖1所示，輕質不可伸長的晾衣繩兩端分別固定在豎直桿M、N上的a、b兩點，懸掛衣服的衣架鉤是光滑的，掛于繩上處于靜止狀態.如果只人為改變一個條件，當衣架靜止時，下列說法正確的是( ).

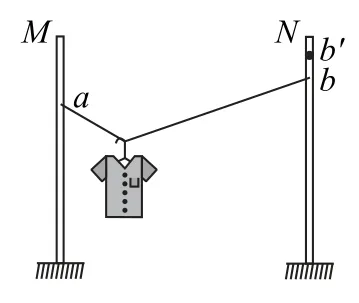
圖1

A.繩的右端上移到b′，繩子拉力不變

B.將桿N向右移一些，繩子拉力變大

C.繩的兩端高度差越小，繩子拉力越小

D.若換掛質量更大的衣服，則衣架懸掛點右移

分析設兩桿間距離為d，繩長為l，Oa、Ob段長度分別為la和lb，則l＝la＋lb，兩部分繩子與豎直方向的夾角分別為α和β，受力分析如圖2所示，繩子中各部分張力相 等，FTa＝FTb＝FT，則α＝β，滿足2FTcosα＝mg，d＝lasinα＋lbsinα＝lsinα，即.繩右端移到b′，d和l均不變，則sinα為定值，α為定值，cosα為定值，繩子的拉力保持不變，故選項A 正確;選項C、D 錯誤;將桿N向右移一些，d增大，則sinα增大，cosα減小，繩子拉力增大，故選項B正確.

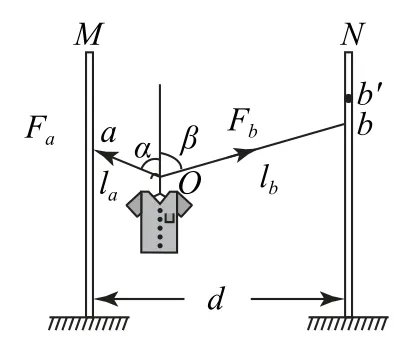
圖2

總結傳統的掛衣架問題涉及兩個關鍵方程，一是基于幾何條件的幾何方程，繩子和豎直方向夾角的正弦值等于兩桿間距與繩長的比值，即;二是基于受力平衡的物理方程2FTcosα＝mg.

抓住這兩個方程，這一類問題就可以輕松破解.接下來我們一一欣賞此模型各種演化進階的形式.

例2晾曬衣服的繩子兩端A、B分別固定在兩根豎直桿上，A點高于B點，原來無風狀態下衣服保持靜止.某時一陣恒定的風吹來，衣服受到水平向右的恒力而發生滑動，并在新的位置保持靜止(如圖3)，不計繩子的質量及繩與衣架掛鉤間的摩擦，下列說法一定正確的是( ).

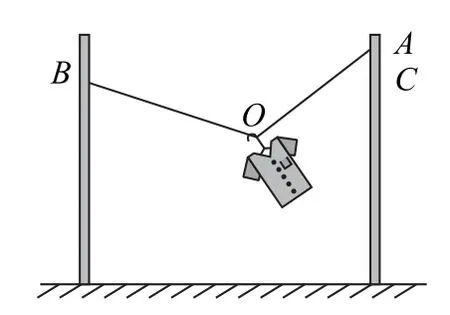
圖3

A.有風時，掛鉤左右兩側的繩子拉力不相等

B.無風時，掛鉤左右兩側繩子OA較陡

C.相比無風時，有風的情況下∠AOB大

D.在有風的情況下，A點沿桿稍下移到C點，繩子的拉力變小

分析本題創設的情境很有意思，衣服受到恒定水平向右的風力，前文中的規律就不適用了，起碼繩子上的力的合力就不等于衣服重力了，那本題怎么解決呢? 聰明的同學會聯想到等效思想，比如在電場中，有時會把恒定電場力和重力合起來，這里也可用這一思想，把衣服重力和風力合成起來，于是得到下圖4-乙:由于掛鉤仍然是光滑的，所以兩端繩上力依然相等，所以重力和風力的合力方向沿∠AOB的平分線，仿照前述列平衡方程有2FTcosα＝F，而幾何方程自然為.

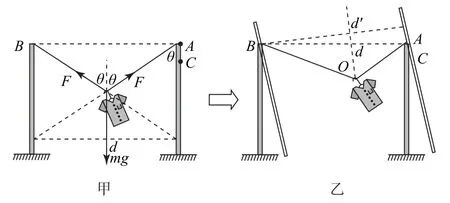
圖4

核心思想依然是一個物理平衡方程和一個幾何方程，只是思維上做了一些切換，一下子就豁然開朗了.顯然繩子沿桿方向從A到C，兩桿等效間距變短，代入幾何與物理方程，可知選項D 正確.

掛衣架傳統問題到此好像就“山窮水復疑無路”了，但是命題專家永遠可以“柳暗花明又一村”，2018年浙江真題就貢獻了下面這個精彩的案例.

例3如圖5所示，一根繩的兩端分別固定在兩座猴山的A、B處，A、B兩點水平距離為16 m，豎直距離為2 m，A、B間繩長為20m.質量為10kg的猴子抓住套在繩子上的滑環從A處滑到B處.以A點所在水平面為參考平面，猴子在滑行過程中重力勢能最小值約為( )(繩處于拉直狀態).

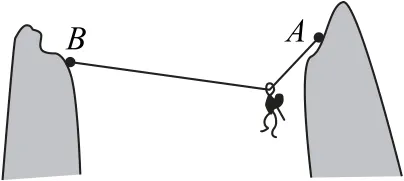
圖5

A.－1.2×103J B.－7.5×102J

C.－6.0×102J D.－2.0×102J

分析命題專家設計此題時，本意是讓學生用類比思想，把猴子問題類比成掛衣架問題解決.

這個問題涉及的思想是最小勢能原理，也就是說猴子重力勢能最小的時候，它在水平方向是平衡狀態.搞清楚猴子水平方向受力平衡，那么問題就劃歸成一個常見的定式.如圖6 所示，猴子在最低點P水平受力平衡，又因為同繩，認為滑環兩邊繩上力相等，即FTsinα＝FTsinβ，作BP延長線與A點鉛垂線交于C點，過B點作BD垂直于D，可得.

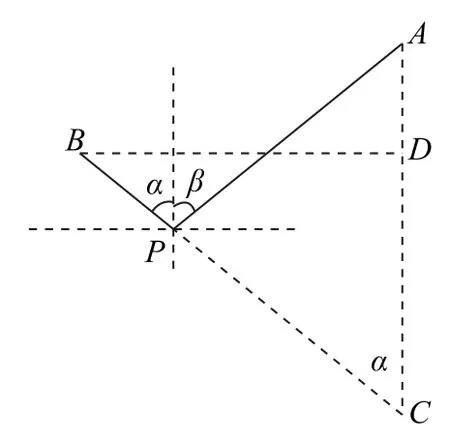
圖6

顯然CD＝BCcosα＝12m，所以P距離A點豎直距離為.本題實際上是前述掛衣架問題的一個逆序思維問題，即在已知物理條件下反推幾何關系的問題.

但實際上此題學生普遍先想到橢圓，使用圓錐曲線知識去求解.

由于猴子到A、B兩點距離之和是20，故猴子運動軌跡是橢圓，焦點是A、B兩點，問題就劃歸成一個傾斜橢圓求橢圓上最低點問題.仍沿著長軸和短軸建立坐標系，如圖7所示.

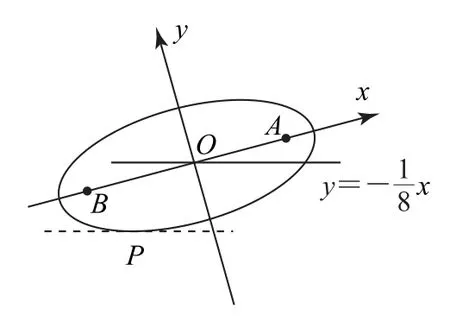
圖7

由題目參數可知，半長軸a＝10，焦距滿足，從而可得橢圓標準方程.

顯然最低點的切線應該沿著水平方向，A、B高度差是2m，水平距離為16 m，所以在此坐標系中該切線斜率，即過原點平行于水平面直線方程為.對橢圓方程進行隱函數求導得，此處(x0，y0)即為橢圓最低點坐標，聯立可得坐標(x0，y0)為(－2.067，－5.788).根據點到直線距離關系有d＝，知d＝6.所以橢圓最低點距離A點的豎直距離是7.考慮猴子并非質點，繼而得知答案選B.

為什么學生做“猴子”問題時普遍想到的是橢圓而不是“掛衣架”呢? 高中生經過大量圓錐曲線訓練，想到橢圓是很自然的事.想不到“掛衣架”模型是因為學生意識到“掛衣架”模型和“猴子”模型本質的不同，猴子在最低點不處于平衡態!

具體問題設置中應用的定式結論不同，“掛衣架”問題核心分析受力動態平衡，即繩子的夾角由懸掛點水平距離和繩長決定，而“猴子”問題核心是求解最低點坐標，利用相似關系解決一個幾何關系.訓練過“掛衣架”的學生沒有經過延伸和拓展，如果只是就題論題，學生可能就拘囿于定式，思維得不到拓展，即便會類比也求解不出結果.

事實上，二者最本質的不同是兩題建模方式不同，“掛衣架”模型指向很清晰，是一個靜態受力平衡問題，難點在于數量關系的處理，學生經過訓練后應對換湯不換藥的問題，本質沒有變，容易把握.但是“猴子”問題變成了一個動態過程，問最低點位置是一個幾何最值，學生建模時很容易受到數學訓練中大量極值問題干擾，喜歡利用函數去解決，沒有意識到此題可以通過物理分析得出結論.而且一般處理最低點問題，都是在豎直方向運動，此題猴子做曲線運動，而且不是學生熟知的曲線運動，在不知曉最小勢能原理情況下，不易分析得出水平受力平衡切向沒有加速度即為猴子軌跡最低點.

既然“猴子”不處于平衡態，為什么這個問題可以用“掛衣架”模型處理方法解決呢? 其物理本質是什么? 這是一個最小勢能原理結合水平方向受力平衡“一繩兩點”定式問題，數學上是基于橢圓軌跡求解最低點問題，那么兩種方法之間有沒有聯系? 如圖8所示，過最低點作橢圓切線，再作切線的法線，連接最低點和橢圓兩個焦點，則連線與豎直方向夾角相等! 這也是橢圓面反射定律的體現，即光源從一個焦點發出光線經過橢圓表面反射后必將匯聚在另一個焦點上.

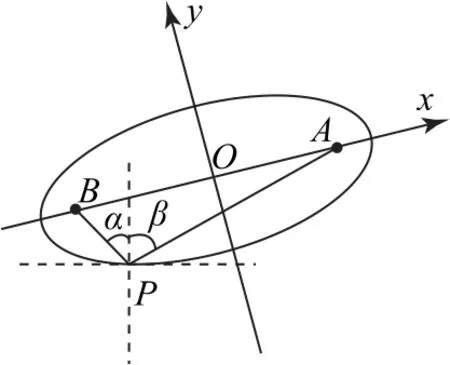
圖8

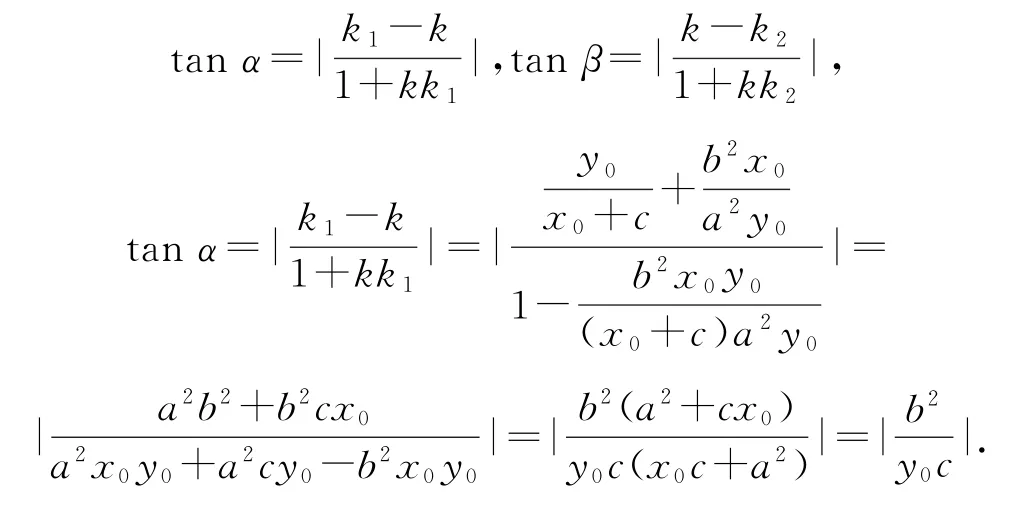
最后，我們用一個綜合問題來總結這一專題內容.

例4如圖9為特種兵過山谷的簡化示意圖，山谷的兩側為豎直陡崖.將一根不可伸長的細繩兩端固定在圖中A、B兩點.繩上掛一小滑輪P，戰士們相互配合，沿著繩子滑到對面.如圖9所示，戰士甲(圖中未畫出)水平拉住滑輪，質量為70kg的戰士乙吊在滑輪上，腳離地處于靜止狀態，此時AP豎直，PB水平，然后戰士甲將滑輪由靜止釋放，戰士乙即可滑到對面公路.不計滑輪大小，也不計繩與滑輪的質量，其中AP＝6m，PB＝8m.

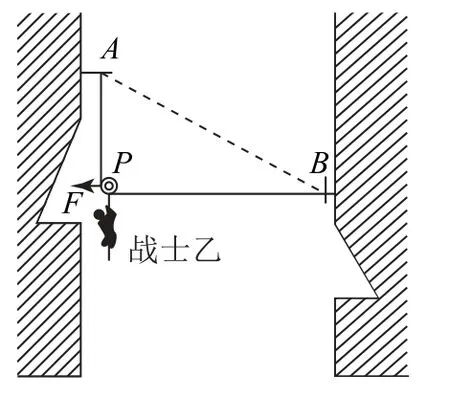
圖9

(1)求戰士甲釋放滑輪前對滑輪的水平拉力F;

(2)若戰士乙運動到右側公路的速率為6 m·s－1，求該過程中克服阻力所做的功;

(3)若戰士乙運動到曲線的最低點時速率為7 m·s－1，該處可看作半徑R＝7 m 的圓的一部分，則戰士乙在最低點時繩AP和PB受到的拉力.

分析(1)對滑輪受力分析，由平衡條件得F＝FT＝mg＝700N.

(2)戰士到達右側時，幾何關系如圖10-甲所示，則82＋(6＋h)2＝(14－h)2，解得h＝2.4 m.由動能定理得，解得W＝420J.

圖10

(3)戰士運動到最低點時，幾何關系如圖10-乙所示，則AC＝8m，AD＝14m，所以

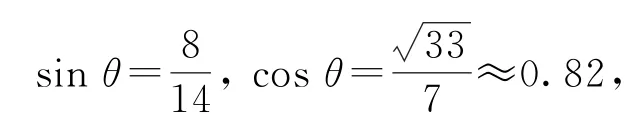
在最低點時由牛頓第二定律得2FTcosθ－mg＝，解得FT≈725.6N.

由牛頓第三定律知，繩子受到的拉力等于繩子對滑輪的拉力為725.6N.

此題除了對幾何作圖有一定要求外，本質上仍然和前述問題一脈相承，和“猴子”問題一樣，戰士在最低點依然不是平衡態，只是水平方向上受力平衡，所以可以用掛衣架問題的幾何方程求出最低點的位置.由于戰士的軌跡是橢圓，于是在使用向心力公式時要注意用曲率半徑，這也是對前述問題的一個補充拓展.

(完)