基于牛頓-歐拉法的三軸線連桿轉向機構數學建模與仿真優化*

楊飛雪 康紹鵬 劉凱磊 強紅賓 吳 昊

(江蘇理工學院機械工程學院，江蘇 常州 213001)

軸線車以其模塊化組合、大載重量和高速運輸等特點在大型特種過程運輸領域中有著較為廣泛的應用。但軸線車在行駛過程中，由于存在轉向精度不高、轉向不夠穩定等問題，會影響軸線車的行駛安全[1]，引發嚴重的交通事故。相較于其他轉向機構，連桿轉向機構由于其能承受更高的載重和更快的速度，而且價格較便宜等優點，適合作為軸線車的轉向機構。

目前常用的多剛體系統動力學的建模方法主要有牛頓-歐拉法、拉格朗日方程法以及凱恩法[2-4]。周春國[5]等人利用對稱性將六連桿機構轉化為以四連桿機構為主并建立了相關數學模型；陳國強[6]等人通過牛頓-歐拉法建立了3-PRS并聯機構動力學模型并分析了機構關節處的摩擦力；王殿軍[7]等人采用拉格朗日法對六自由度搬運機器人進行了動力學分析并通過Adams仿真得了轉動關節的力矩曲線；王冰冰[8]等人從能量的角度出發，利用拉格朗日方程法建立卡登園行星機構的動力學模型，分析出了機構的運動規律；楊文斌[9]等人采用凱恩法建立了三柱塞式乳化液泵的動力學模型，分析了曲柄與連桿的長度比λ、曲軸驅動角速度ω對連桿慣性力的影響。

相較于其他建模方法，牛頓-歐拉法原理明朗且能夠較為清晰地描述三軸線連桿轉向機構，本文使用牛頓-歐拉方法對三軸線運輸車連桿轉向機構進行數學建模并通過Simulink與Adams對其進行優化以減少軸線車的轉角誤差，提高轉向的穩定性。

1 連桿轉向機構的數學建模

1.1 數學建模原理

牛頓-歐拉法是多剛體動力學領域使用較為廣泛的建模方法，它首先需要建立慣性坐標系和機體坐標系[10]，再分別對多剛體系統的各個桿件進行受力分析[11]，列寫力和力矩方程，最后結合運動學方程得到完整的動力學模型。以下式(1)中兩個等式分別為Newton和Euler方程：

(1)

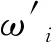
1.2 運動學模型

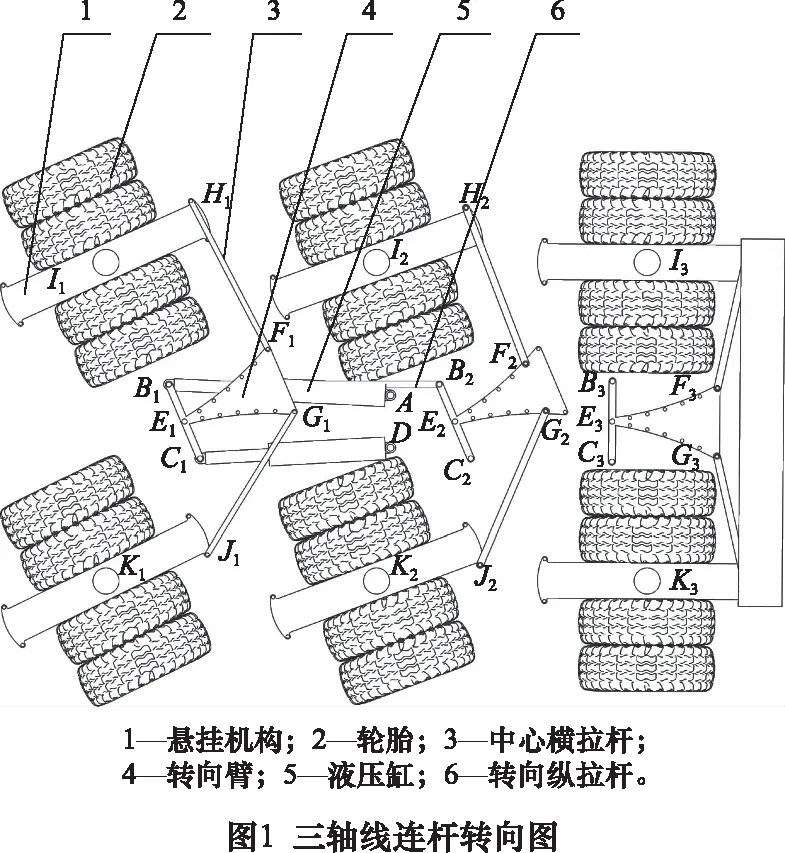
如圖1所示，三軸線連桿轉向機構中每個軸線有兩個輪胎組，共計24個輪胎。從左到右分別為第一軸線、第二軸線和第三軸線。其中，由鉸接在車架上的液壓缸的伸縮帶動轉向臂轉動一定的角度，然后帶動鉸接在轉向臂上的兩個橫拉桿運動，而橫拉桿推動車輪上方的懸掛機構，懸掛機構帶動輪胎的轉動從而實現車輪按一定的角度進行轉向。與此同時，轉向臂的轉動還會帶動縱拉桿完成下一軸線的轉向臂的轉動，實現軸線車的整體轉向。圖1中鉸接點位Bi、Ei、Fi、Gi、Hi、Ji、Ii、Ki(i=1,2)是三軸線連桿轉向機構數學建模以及仿真優化研究的關鍵點位。

圖2為三軸線車在道路上轉向行駛示意圖，三軸線車沿車速v的方向行駛，并在行駛過程中轉向。根據阿克曼理論，三軸線車在轉向時第三軸線輪胎不轉動，以三軸線車在開始位置和終點位置的第三軸線交點為坐標原點，建立如圖2所示的Oxy坐標系。三軸線車在轉向行駛過程中轉動θ。

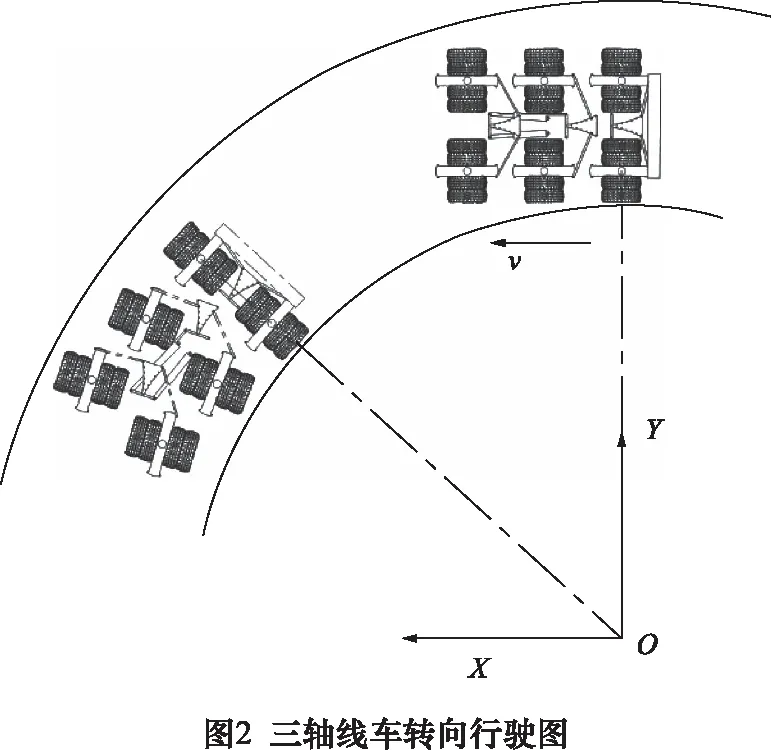
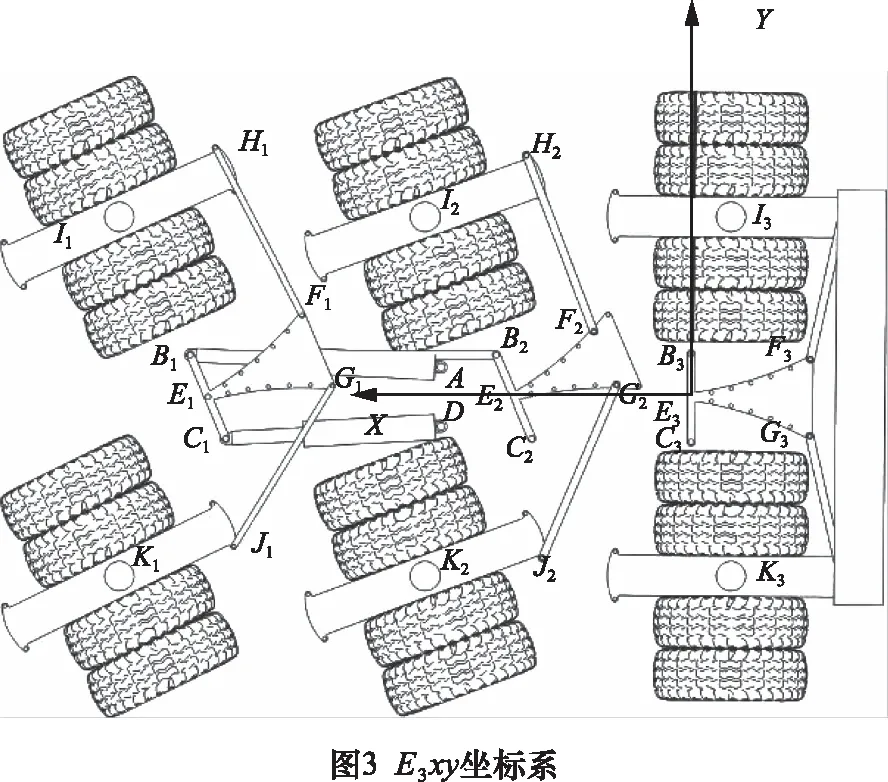
在圖2所示的轉向過程中，可以求得Bi、Ei、Fi、Gi、Hi、Ji、Ii、Ki(i=1,2)等關鍵點位在Oxy坐標系下的坐標。車輛在行駛狀態下直接求各個關鍵點位在Oxy坐標系下的坐標比較困難，可以先以三軸線車的第三軸線的轉向臂中心(E3)為原點建立如圖3所示的E3xy坐標系，求得各點位在E3xy坐標系下的坐標A，然后求得E3xy坐標系相對于Oxy坐標系的變動B,最后求得各點在Oxy坐標系下的坐標C。其中：

C=A·B

液壓缸的動力輸出取決于車輛的目標轉角，本文中用液壓缸伸縮桿的長度變化來描述液壓缸動力輸出。設定第一軸線外側的轉角α11范圍為0～40°，轉角加速度為a=2°/s，則α11=0.5×a×t2，時間t為0～6.3 s。根據阿克曼原理[12]可以逆推到轉向臂此時的理論轉角為：

β=arctan(3.1/(3.1/tan(α)-0.91))

(2)

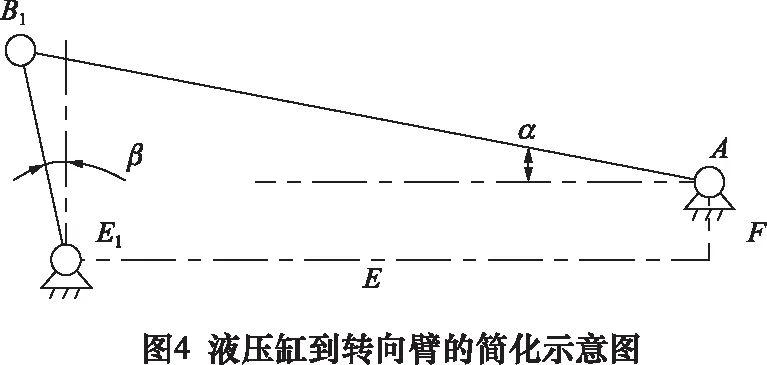
根據此時的轉向臂理論轉角可以繼續逆推到液壓缸伸縮桿的變化量。將液壓缸(AB1)到轉向臂之間的桿件(B1E1)進行簡化，如圖4所示，根據其矢量關系建立方程并將其分解到x軸和y軸上，建立如式(3)所示的方程組。

(3)

式中：E為液壓缸的鉸接點到轉向臂中心的鉸接點的橫向距離，E=1.18 m；F為液壓缸的鉸接點到轉向臂中心的鉸接點的縱向距離，F=0.15 m。

對式(3)求解可得液壓缸(AB1)的長度，可進一步求得液壓缸在軸線車逆時針轉動上的伸長量l：

(4)

在完成以上的反解后再進行正向建模，根據圖3求得正解后的轉向臂轉角β1：

β1=arccos((l×sin(α)+0.152)/0.23)

(5)

三軸線連桿轉向機構第一軸線外側的連桿機構，簡化示意圖如圖4所示，由轉向臂的外側邊(E1F1)、轉向橫拉桿(F1H1)和懸掛機構(H1I1)的簡化桿件組成。E1F1為主動桿件，帶動F1H1的轉動，然后推動H1I1繞I1點轉動。

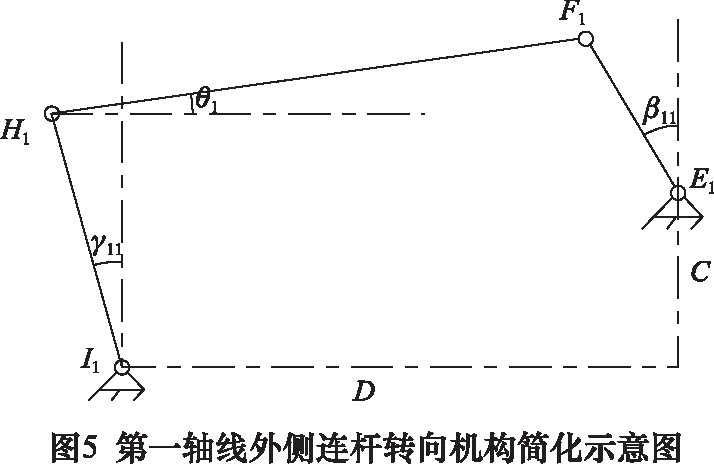
對如圖5所示的連桿機構進行運動學分析，可以得到式(6)：

(6)

式中：γ11為懸掛機構與過I1點的縱向中心線之間的夾角；β11為轉向臂外側邊與過E1點縱向中心線之間的夾角；D為懸掛機構中心到轉向臂中心的橫向距離，D=0.91 m;C為懸掛機構中心到轉向臂中心的縱向距離，C=0.45 m。

對式(6)求解可以求得γ11與β11的關系，進一步求得第一軸線外側輪胎轉角與轉向臂轉角的關系。

同理，對第一軸線內側、第二軸線外側和第二軸線內側的連桿轉向機構進行運動學分析可得第一軸線內側懸掛機構轉角與第一軸線轉向臂轉角，第二軸線外側懸掛機構轉角與第二軸線轉向臂轉角，第二軸線內側懸掛機構轉角與第二軸線轉向臂轉角之間的關系。

1.3動力學模型

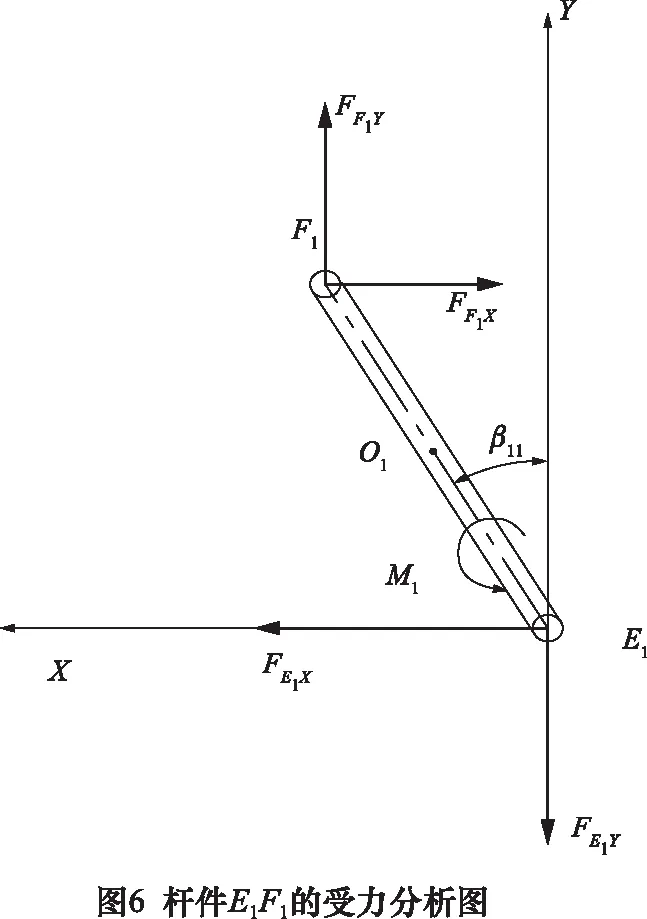
通過牛頓-歐拉法建立動力學模型需要將三軸線連桿轉向機構拆分為單獨的構件，然后對其構件進行逐個分析。將圖5所示的第一軸線外側連桿轉向機構簡化示意圖進行分解，對其中轉向臂的外側邊(E1F1)、轉向橫拉桿(F1H1)和懸掛機構(H1I1)的簡化桿件進行單獨受力分析。圖6為桿件E1F1的受力分析圖，對其構建如式(7)所示的動力學方程。

(7)

式中：FE1X是車架施加在轉向臂中心上的約束反力的X分量；FF1X是轉向橫拉桿施加在轉向臂上的約束反力的X分量；mE1F是轉向臂的質量；FE1Y是車架施加在轉向臂中心上的約束反力的y分量；FF1Y是轉向橫拉桿施加在轉向臂上的約束反力的y分量；M1是轉向臂的主動轉向力矩；JO1是主動杠的轉動慣量。

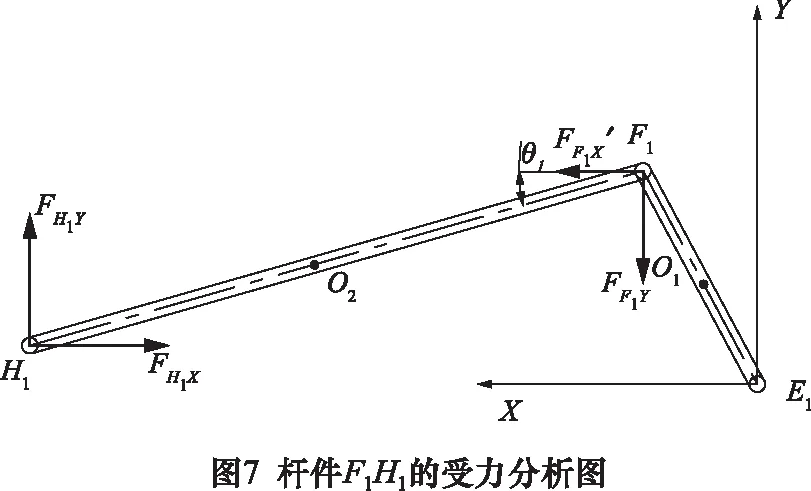
對轉向橫拉桿(F1H1)的受力分析如圖7所示，對其構建如式(8)所示的動力學方程。

(8)

式中：FF1X′是轉向臂施加在轉向橫拉桿上的約束反力的X分量；FH1X是懸掛機構施加在轉向橫拉桿上的約束反力的X分量；mF1H1是轉向橫拉桿的質量；FF1Y′是轉向臂施加在轉向橫拉桿上的約束反力的Y分量；FH1Y是懸掛機構施加在轉向橫拉桿的約束反力的Y分量；ω1是轉向橫拉桿的轉動角速度；JO1是轉向橫拉桿的轉動慣量。

對轉向橫拉桿(H1I1)的受力分析如圖8所示，對其構建如式(9)所示的動力學方程。

(9)

式中：FH1X′是轉向橫拉桿施加在懸掛機構上的約束反力的X分量；FI1X是地面施加在懸掛機構上的約束反力的X分量；mF1H1是懸掛機構的質量；FH1Y?是轉向橫拉桿施加在懸掛機構上的約束反力的Y分量；FI1Y是地面施加在懸掛機構上的約束反力的Y分量；JO3是懸掛機構的轉動慣量。M2是輪胎的回正力矩。

在以上的動力學模型中，Oi(i=1,2,3)分別是桿件E1F1、F1H1、和H1I1的質心，坐標分別為(E1+F1)/2，(F1+H1)/2和(H1+I1)/2。vOi(i=1,2,3)為Oi(i=1,2,3)的速度，其中Oi(i=1,2,3)點的速度、加速度可以通過對Oi(i=1,2,3)點的坐標進行一階導、二階導求得。對于各點的受力F和F′是一對反作用力，F′=-F。對于ω1可以通過如下的方法用轉向臂轉角與輪胎轉角來表達。

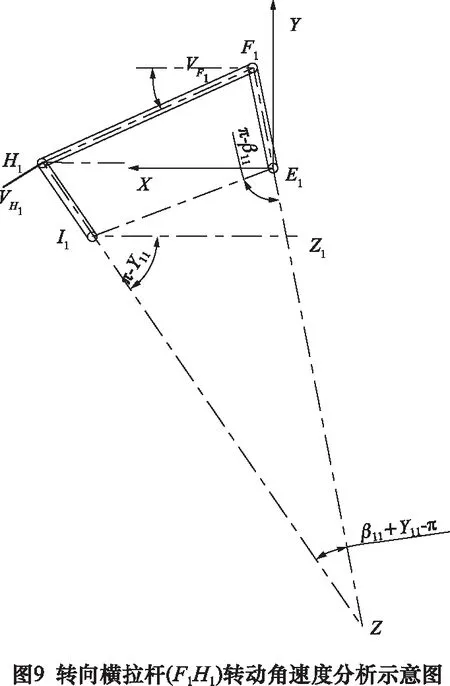
如圖9所示，將E1F1、I1H1反向延長交于一點Z,可求得∠ZI1Z1=π-γ11，∠I1E1Z=π-β11，∠I1ZZ1=β11+γ11-π。根據正弦定理

(10)

由等式(10)可以求得F1Z的長度。在圖9中的第一軸線外側連桿轉向機構中，簡化桿件E1F1為主動桿件，在液壓缸的推動下繞轉向臂中心(E1)作圓周運動，懸掛機構簡化桿件(I1H1)繞懸掛機構中心(I1)作圓周運動，可以求得:

(11)

vF1=F1Z×ω1

(12)

由等式(11)、(12)可求得第一軸線外側連桿轉向機構的轉向橫拉桿的轉動角速度ω1。

之后的第一軸線內側、第二軸線外側和第二軸線內側的動力學建模與之相似。根據阿克曼理論，該三軸線車的第一軸線的輪胎在轉向時轉角最大，第二軸線輪胎轉角較小，第三軸線輪胎不轉向。

2 仿真與優化

對三軸線連桿轉向系統的模型通過MATLAB搭建相應的Simulink模型[13]，同時在Adams中搭建相應的動力學模型，其具體點位如表1所示。在該模型中，轉向連桿材料為Q345鋼，連桿鉸接處的運動副有潤滑處理，其摩擦系數取0.07，間隙配合選用H9/f9。其中轉向臂上的孔位初始坐標如表2所示，通過Simulink進行仿真得到如圖10所示的第一軸線與第二軸線的輪胎轉角變化圖。其中，γ11是三軸線運輸車逆時針轉向時第一軸線外側輪胎轉角，γ12是第一軸線內側輪胎轉角，γ21是第二軸線外側輪胎轉角，γ22是第二軸線內側輪胎轉角。

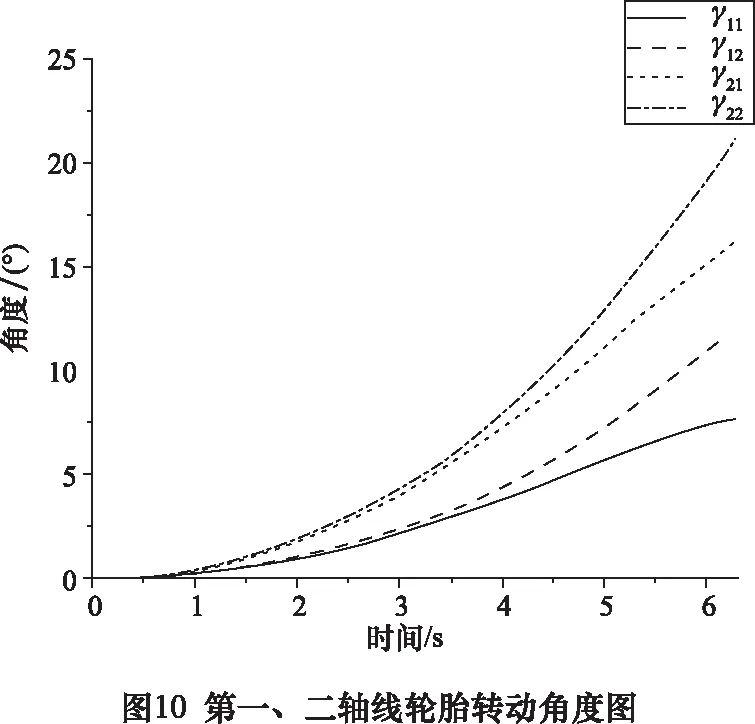
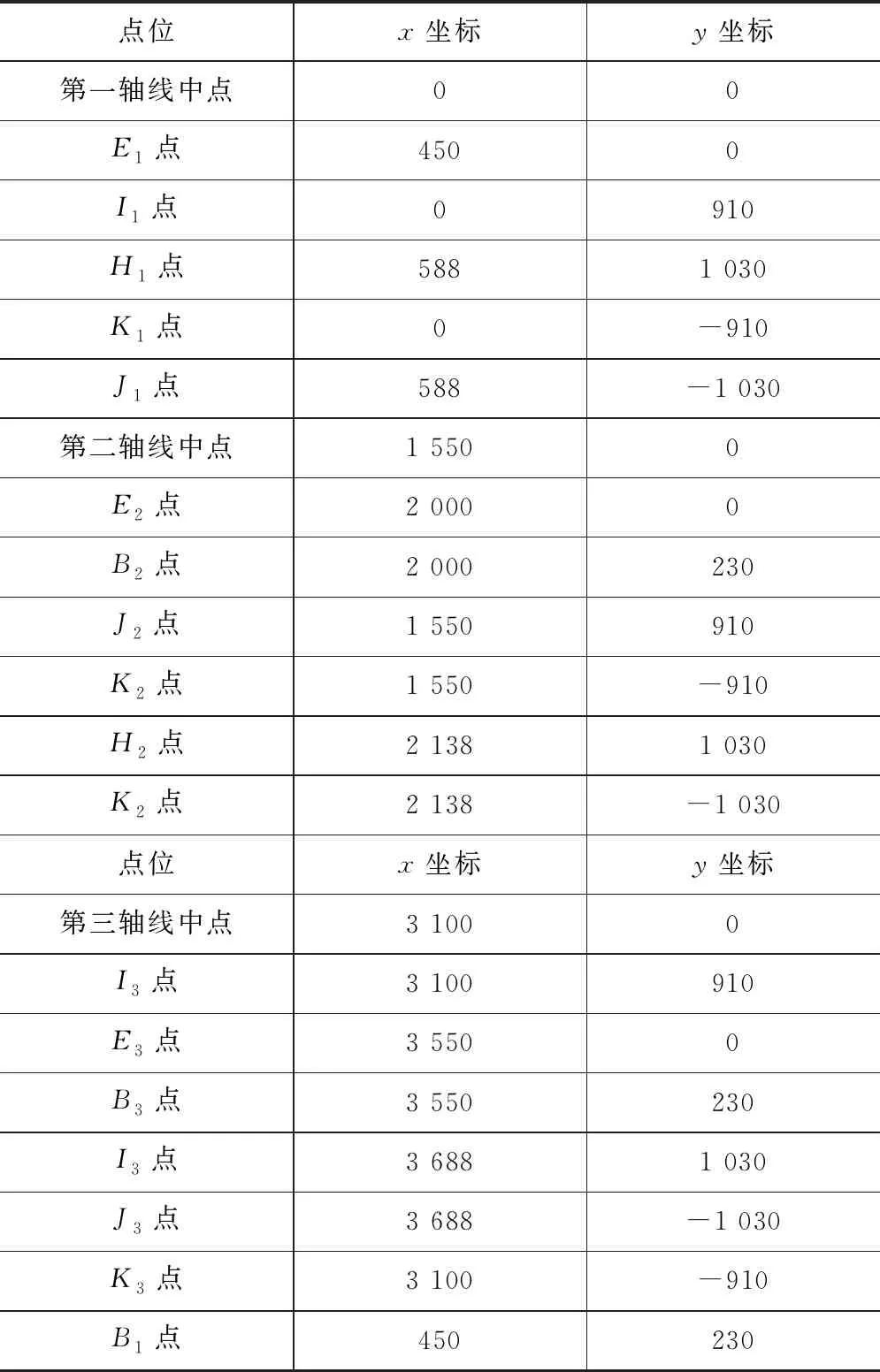
表1 Adams模型點位表

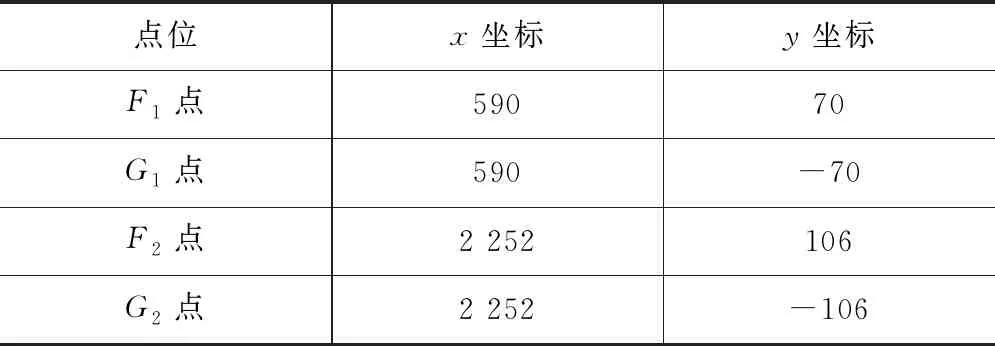
表2 轉向臂上的孔位初始數據

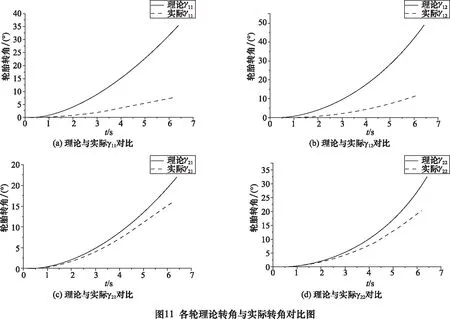
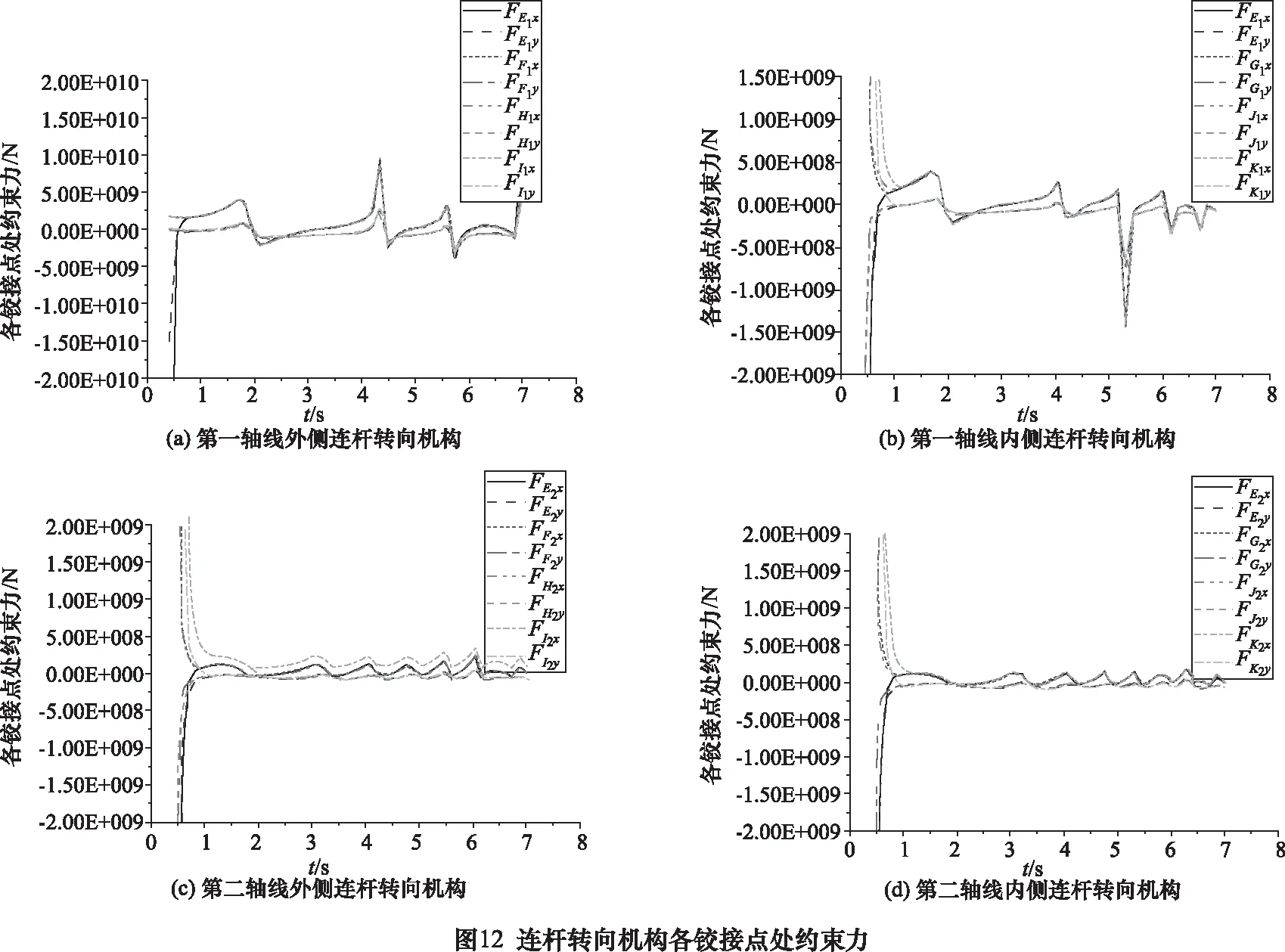
基于上述條件，通過Adams動力學模型進行仿真得到各輪的實際轉角，將該實際轉角與符合阿克曼理論的理論轉角進行對比，如圖11所示，可以看出各軸線上的輪胎的實際轉角與理論轉角存在著較大的誤差。第一軸線的內外側輪胎轉角誤差分別為27.5°、32.5°，第二軸線的內外側輪胎轉角曲線則較為接近，誤差分別為5.9°、11.51°，第一軸線外側、第一軸線內側、第二軸線外側、第二軸線內側的連桿轉向機構上的各鉸接點的受力情況分別如圖12所示。

針對4組轉向輪胎轉角誤差較大的情況，對其進行優化，優化目標為理論轉角與實際轉角的差在優化范圍內取得最小值，并且優化后的差值小于2.5°。通過數學模型分析，三軸線連桿轉向機構中的4組轉向輪胎轉角受連桿的角度和長度影響較大，而連桿角度和長度由第一軸線和第二軸線的轉向臂與內外側轉向橫拉桿的鉸接點空間位置所決定。因此，將第一軸線和第二軸線轉向臂上的4個鉸接點(F1點、G1點、F2點和G2點)孔位坐標值作為優化對象，并進行參數化，通過Simulink與Adams聯合仿真對4個鉸接點的坐標進行優化[14-16]，其優化范圍為各鉸接點x坐標絕對值上增加0到420個單位，y坐標絕對值上增加0到200個單位。

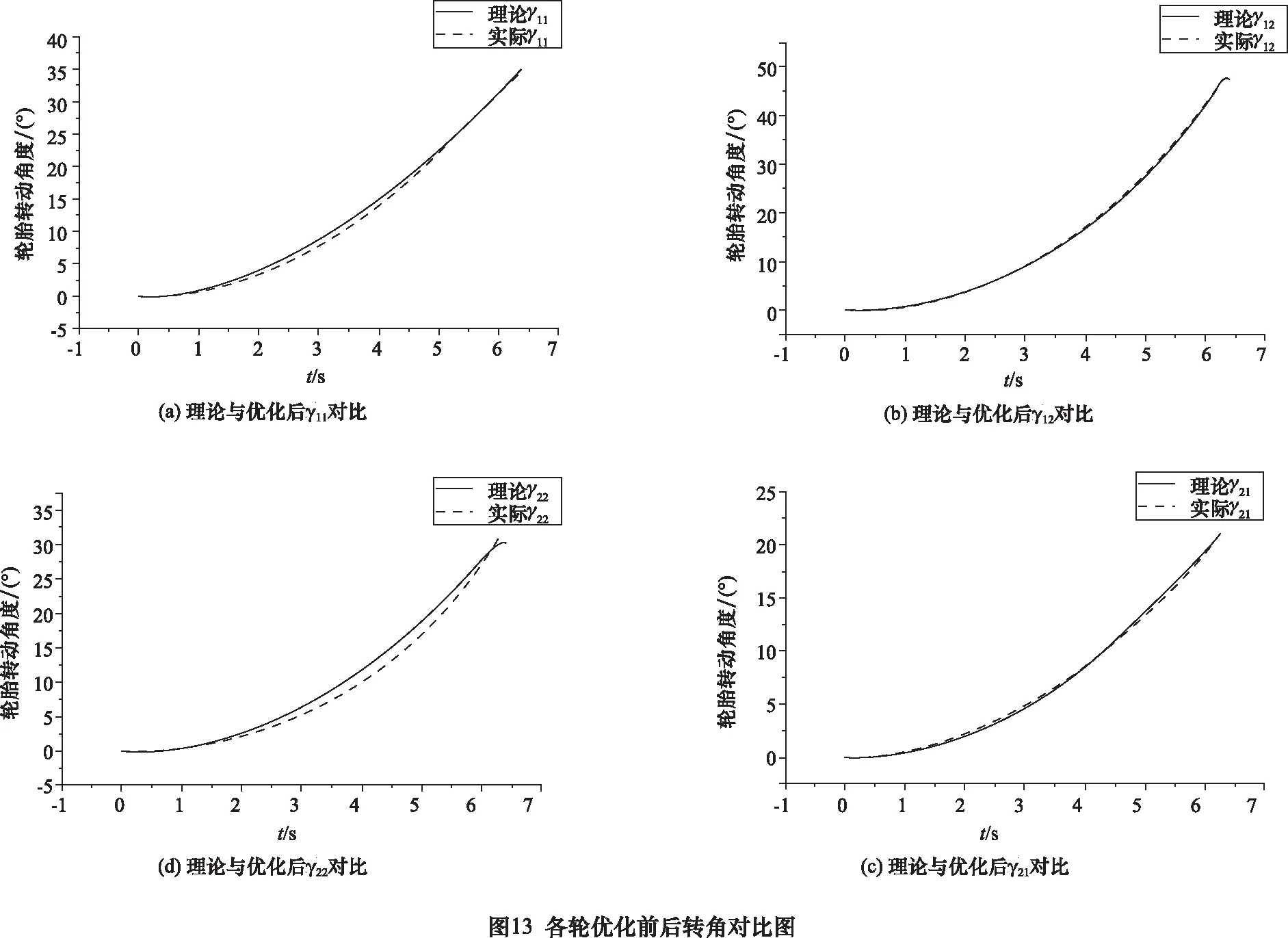
將Simulink模型中的第一軸線轉向臂轉角作為驅動輸入，對4個鉸接點坐標值進行優化，其結果如表3所示。將點位優化后的各輪實際轉角與理論轉角進行對比，如圖13所示。

表3 轉向臂上的孔位優化后數據

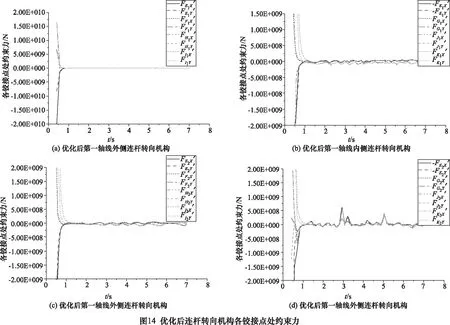
由圖13的各輪的理論轉角與優化后的實際轉角對比可以看出，各軸線的轉向臂上的點位采用如表2的優化后的點位后與遵循阿克曼原理的理論轉角之間的最大誤差小于2.5°，第一軸線內外側以及第二軸線外側的輪胎轉角誤差較小，最大為1.2°左右，最大的轉角誤差出現在第二軸線內側輪胎，最大為2.2°左右，但仍在誤差允許的范圍內。經過優化后各點位的受力與優化前的對比如圖14所示。

將圖12和圖14進行對比可以看出經過優化后，各鉸接點受力相較于優化前會更穩定，尤其是第一軸線外側的各點不僅受力更小，且受力的穩定性提高較為明顯。

3 結語

(1) 使用牛頓-歐拉法對三軸線連桿轉向機構進行數學建模，得到了連桿轉向機構的位置、轉角速度以及轉角加速度的方程。

(2) 使用MATLAB中的Simulink功能與Adams對三軸線連桿轉向機構搭建運動學和動力學模型。

(3) 通過Simulink與Adams對三軸線連桿轉向機構的模型進行聯合仿真，優化了轉向機構的轉角精度，將最大轉角誤差降低到2.2°以下。

(4) 通過比較優化前后的鉸接點位的約束力，驗證了機構優化對于提升連桿轉向機構的轉向穩定性的有效性。