面向多運輸任務的節能單負載AGV路徑規劃研究*

李俊蘭 張中偉 吳立輝 武照云

(河南工業大學機電工程學院，河南 鄭州 450001)

智能制造已成為全球制造業發展的重要趨勢，在“工業4.0”智能制造框架內，智能物流被認為是實現智能制造的核心與關鍵[1]，而自動導引運輸車(automated guided vehicle，AGV)則是實現智能物流的重要物料運輸設備。隨著全球應對氣候變化壓力的持續增大，制造業節能減排意識不斷提高。物料運輸系統是車間制造系統的重要組成部分，其能耗是車間生產能耗中不可忽視的部分。然而，車間節能生產研究長期聚焦在機床，以AGV為代表的物料運輸設備較少被關注[2]。因此，研究AGV運輸過程的能耗優化問題，對于車間節能生產具有重要的現實意義。

能耗建模是能耗優化的基礎技術。圍繞AGV能耗建模，目前主要從車輛運動角度進行能量分解，考慮一些實際應用環境因素，如車輛結構特性，電池充放電效率等，基于物理運動學理論進行研究[3-5]。這些工作為量化評估和預測AGV運輸能耗提供了指導。進而，一些學者開展了AGV能耗優化研究，例如：王晨曦[6]研究了作業車間AGV綠色物流調度問題，建立了以AGV能耗和調度時間為目標的AGV物流調度優化模型，并提出了一種改進遺傳粒子群算法進行求解；筆者研究團隊建立了以運輸距離和能耗為優化目標的節能單負載AGV路徑規劃模型，分別提出了兩階段求解方法和基于粒子群優化算法(particle swarm optimization，PSO)的求解方法[5-7]。然而，目前AGV能耗優化研究非常有限，總結可得出結論：①節能路徑規劃是提升AGV使用能效的一種可行方法，能耗可作為AGV路徑規劃的獨立優化目標；②當AGV執行多項運輸任務時，任務的執行順序會影響節能效果，但當前研究主要面向單負載AGV和單項運輸任務，缺乏有效的面向多運輸任務的節能AGV路徑規劃(energy-efficient AGV path planning，EAPP)理論和方法指導。

針對現有AGV能耗優化研究存在的問題和不足，本文以離散制造車間環境下的單負載AGV為研究對象，進行面向多運輸任務的EAPP研究，建立了以運輸距離和能耗為優化目標的EAPP模型，進而提出一種兩階段求解方法，并通過案例研究驗證了模型的節能有效性。

1 問題描述與建模

1.1 模型假設

面向多運輸任務的EAPP研究用拓撲地圖表示車間環境，將AGV運輸網絡抽象為一個無向圖G=(V,A)，其中V={1,2,…，n}是車輛裝/卸貨、道路交叉位置等具有特殊意義的節點集合，A={(i,j):i,j∈V,i≠j}是節點之間路徑的邊集合，且邊(i,j)的權重用直接連接節點i和j的路段距離dij表示。在筆者研究團隊前期AGV運輸過程能耗建模研究假設的基礎上[7]，本研究增加以下與運輸任務相關的假設條件：

(1)所有運輸任務零時刻下達，且AGV可用。一旦AGV開始執行運輸任務，不能中斷或者取消。

(2)AGV初始不在任意運輸任務的起始節點，執行各運輸任務時不允許后退或形成回路。當執行完最后一項運輸任務，AGV停在其目標節點。

1.2 模型表示

對于零時刻下達的m項運輸任務，各任務k(k=1,2,…,m)的取貨起始節點Pk和運輸目標節點Ck事先給出，Pk,Ck∈V，且Pk≠Ck。定義決策變量xkq表示運輸任務k和q(q=1,2,…,m，且k≠q)的執行順序：

設AGV空載質量為m0，最大載重量為Q。基于研究假設，AGV執行完全部運輸任務，交替出現的空載和負載運輸階段總數為2m。AGV在各運輸階段的行駛路徑可用其遍歷過的有序節點組成的集合Sl表示，l=1,2,…,2m，Sl?V，且2≤|Sl|≤n。當l=1,2,…,m時，Sl表示AGV在與運輸任務序號相對應的負載運輸階段行駛路徑；當l=m+1,m+2,…,2m時，Sl表示AGV在第l-m個空載運輸階段行駛路徑。給定Sl時，基于研究假設和物理動力學理論可確定AGV到達各運輸任務k起始節點、目標節點的時間TPk和TCk。進而，以全部運輸任務的總完成時間Ttotal作為分析AGV能耗的時間邊界，其可表示為：

Ttotal=max{TCk},k=1,2,…,m

(1)

分析AGV總運輸Etotal需要先計算各運輸階段的AGV能耗，然后累加求和。時間邊界以及AGV運輸過程能耗的分析計算方法可參考文獻[7]。此外，定義整數決策變量yijl來反映各運輸階段AGV行駛經過的邊信息：

AGV總運輸節點間距離D則可表示為：

(2)

EAPP模型優化目標可表示為：

(3)

約束為：

m0≤Mk≤m0+Q,?k

(4)

TPq-TCk+H(1-xkq)≥0,?k,q

(5)

TPk-TCq+Hxkq≥0,?k,q

(6)

(7)

(8)

(9)

約束條件式(4)中Mk為AGV執行運輸任務k時的車輛和貨物總重，該式表示AGV在任一負載運輸階段的載荷不應超過其載重極限。式(5)和(6)表示任意兩個負載運輸階段不允許時間重疊，其中H是一正極大數，從而可以確定運輸任務執行順序。式(7)和(8)分別表示在各運輸階段規劃路徑Sl中包含的每個節點只能被訪問一次和只能通過一條邊離開。式(9)用來約束AGV在各運輸階段不允許后退和環路行駛。

2 模型求解

AGV在各空載/負載運輸階段的可行規劃路徑Sl往往不唯一，各運輸階段路徑規劃最優難以保證整體路徑規劃效果最優。為此，提出一種兩階段方法求解EAPP模型，其流程如圖1所示。

在第1階段，借鑒現有研究成果，例如利用PSO[7]搜索AGV在車間任意兩個不同節點間空載行駛時的最佳節能路徑，記錄對應的Pareto解集。由于各運輸任務初始節點、目標節點和工件質量等信息已知，針對每項運輸任務對應的負載運輸階段，同法搜索AGV最優節能運輸路徑，并記錄對應的Pareto解集。這些記錄信息作為第2階段利用非支配排序遺傳算法(non-dominated sorting genetic algorithm-II，NSGA-II)解決運輸任務優化排序以及局部運輸階段最優運輸路徑的組合優化問題，進而獲得完成全部運輸任務的最優運輸路徑的基礎信息。在第2階段，研究重點關注反映問題可行解的種群個體編碼方案和遺傳算子設計。

(1)個體編碼

個體編碼應能夠反映影響優化目標的決策變量xkq和yijl的信息，設計了一種分段編碼的個體編碼方案，其示例如圖2所示。

個體染色體長度統一為3m，采用實數編碼，全部運輸任務序號隨機分布在前m個基因上；中間m個基因從左到右，按運輸任務序號由小到大的順序依次記錄與各運輸任務對應的負載運輸階段選擇的最優運輸路徑；最后m個基因從左向右，按空載運輸階段順序依次記錄各空載運輸階段選擇的最佳行駛路徑。

(2)遺傳算子

選擇算子沿用標準NSGA-II中的錦標賽選擇策略[8]，構建容量是種群規模一半的配對池，后續交叉、變異操作以從配對池中隨機選擇的個體為父代。

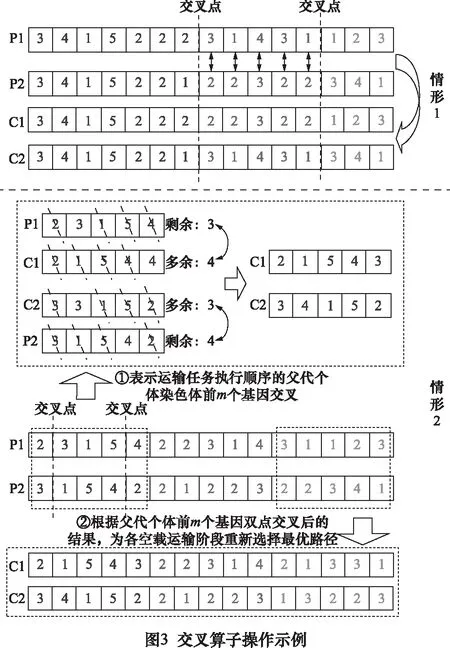
設計了兩種交叉算子，示例如圖3所示。若兩父代個體前m個基因相同，則對它們的后2m個基因進行雙點交叉操作；否則先雙點交叉前m個基因，并進行合法性校驗：依次比對交叉后的子代和父代個體的前m個基因，然后將父代剩余基因按順序依次替換子代多余基因。進而，子代個體根據交叉后的前m個基因，為各空載運輸階段重新選擇最優路徑，更新最后m個基因。

針對變異操作，設計了3種使用幾率均等的變異算子：①在前m個基因中任選兩個不同的基因位，交換其基因值，進而為各空載運輸階段重新選擇最優行駛路徑，更新最后m個基因；②保持前m個基因不變，隨機選擇一項運輸任務，從其對應的最優運輸路徑Pareto解集中隨機挑選一個不同于當前選擇的解，進而更新相應基因位的值；③保持前m個基因不變，隨機選擇一個空載運輸階段，從其對應的最優行駛路徑Pareto解集中隨機挑選一個不同于當前選擇的解，并更新相應基因位的值。

NSGA-II中非支配排序、擁擠度計算等關鍵算法過程可參考文獻[8]，在此不再贅述。

3 案例研究

結合某航空制造企業的一個制造車間[7]進行案例研究，該車間運輸網絡拓撲地圖如圖4所示。

車間現有表1所示的5項常見運輸任務。AGV初始停靠在節點44，其技術參數可參考文獻[7]。兩階段EAPP模型求解方法在Intel core(TM)i7-8700 3.20GHz CPU，24GB RAM，Windows 10的PC用Matlab語言實現，階段1利用PSO[7]搜索AGV執行各運輸任務的最優節能路徑(如表2所示)和在車間任意兩個不同節點間空載行駛的最優節能路徑；階段2使用NSGA-II時的關鍵參數設置如表3所示。

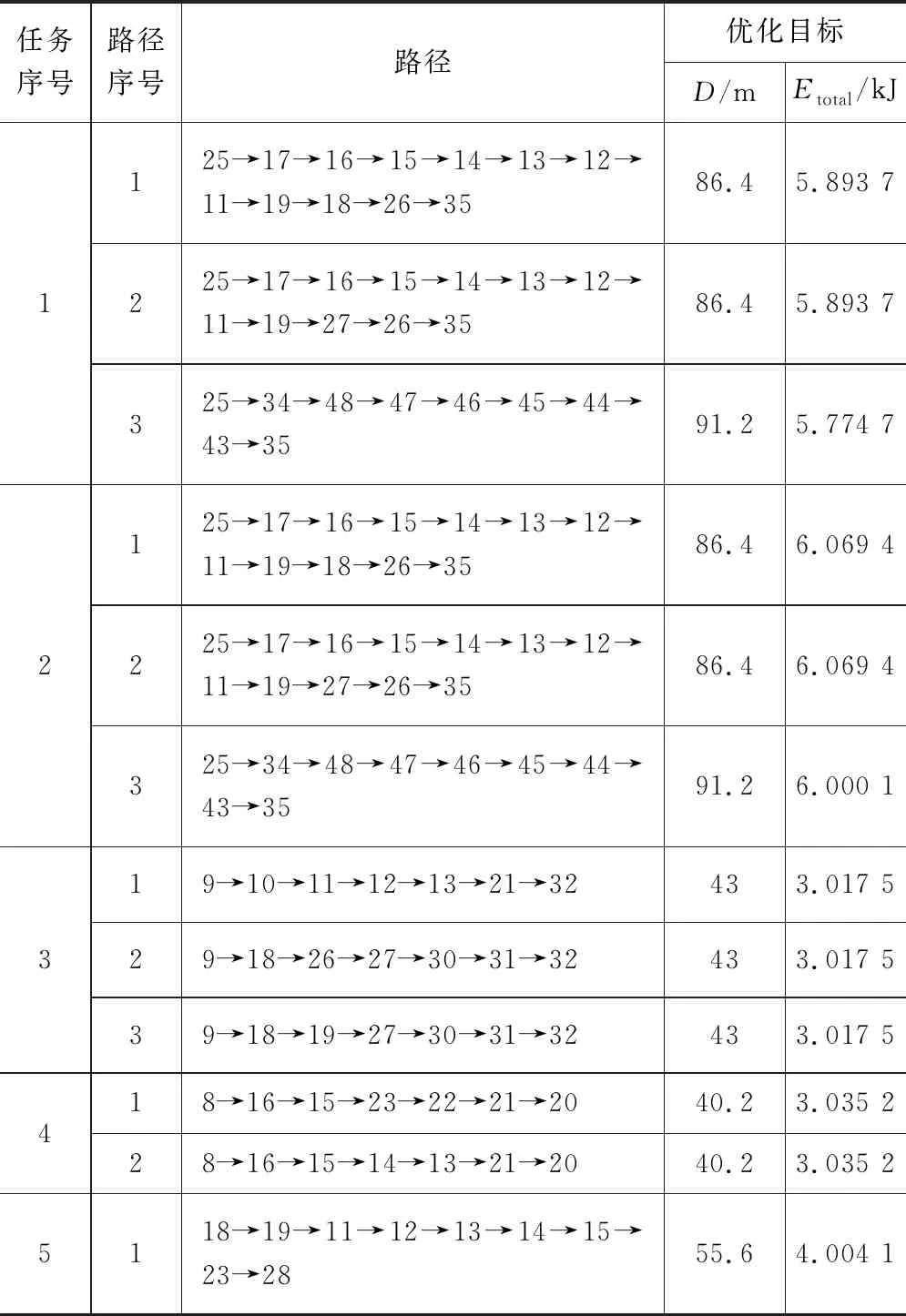
表2 AGV執行各運輸任務的最優節能路徑

表3 NSGA-II參數設置

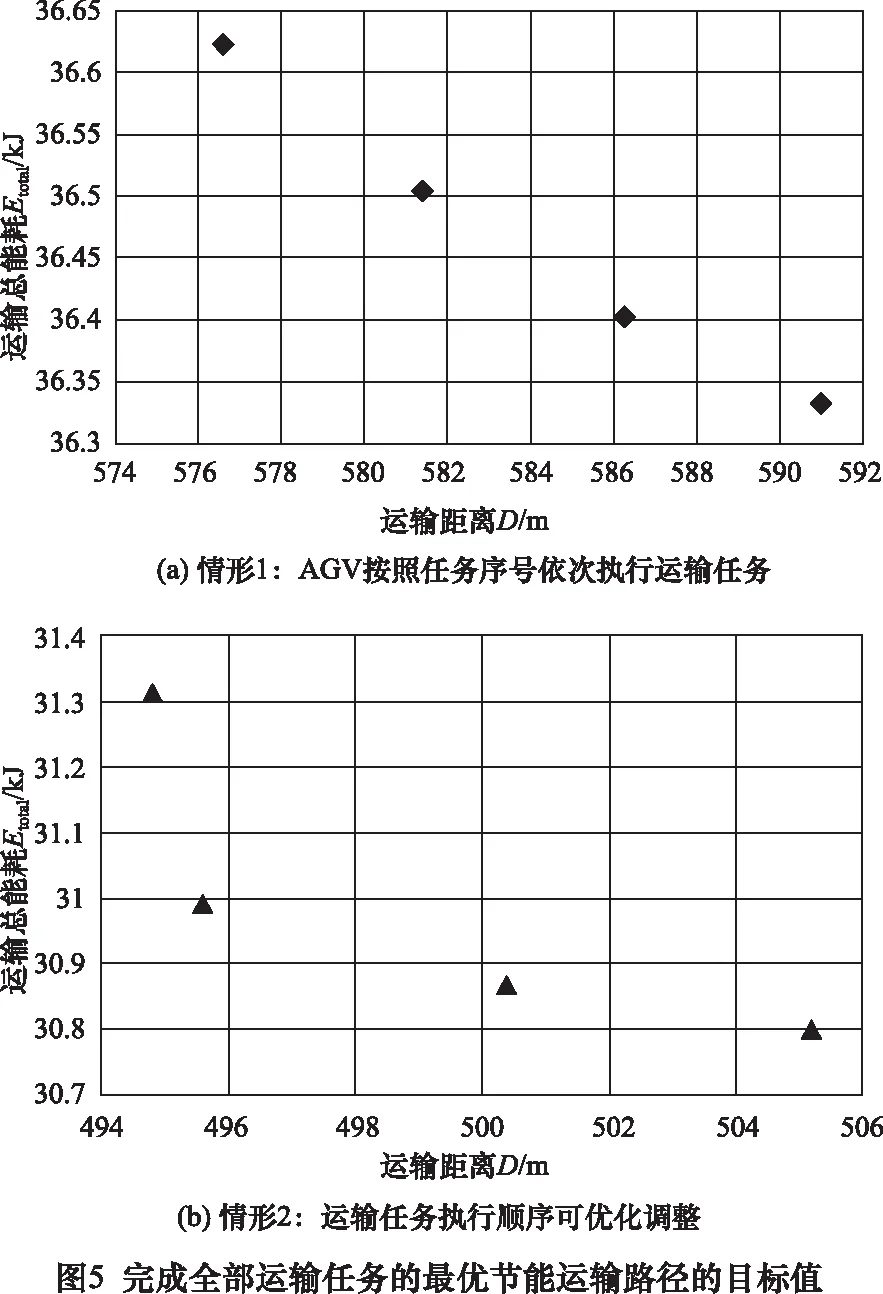
為驗證應用EAPP模型的節能效果，分兩種情形討論。情形1與車間現行計劃一致，AGV按照任務序號依次執行運輸任務；情形2下AGV執行運輸任務的順序可優化調整。兩種情形下求解模型得到的Pareto解對應的優化目標值如圖5所示。

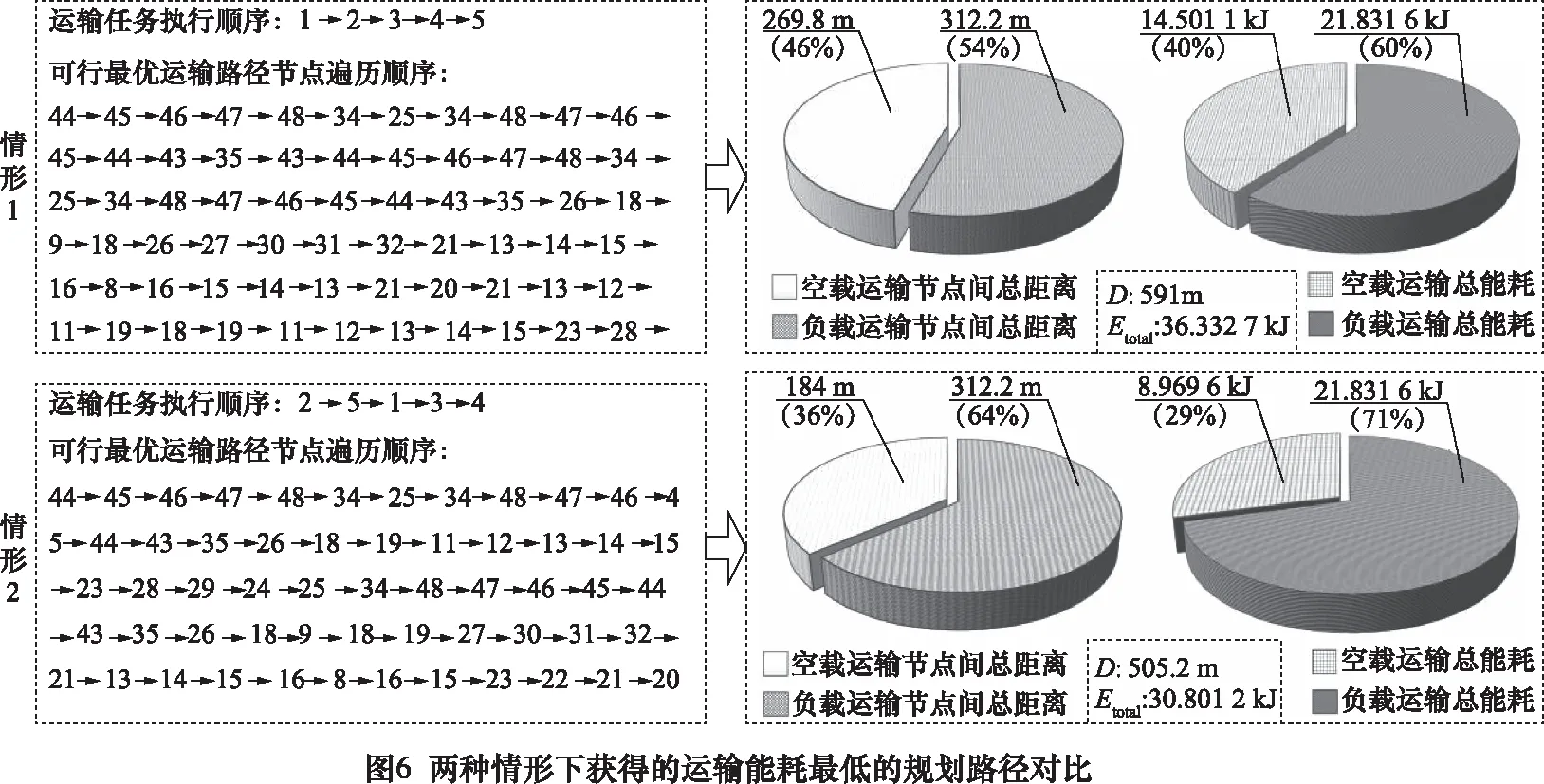
為對比能耗優化效果，在兩種情形下分別隨機選擇一個對應最低運輸能耗的Pareto解進行分析，如圖6所示。情形2與情形1相比，Etotal降低了15.2%，D縮短了14.5%。然而，兩種情形下負載運輸階段的總能耗和總節點間距離相等，說明負載運輸階段優化效果相同。情形2下總體優化效果之所以更優是因為運輸任務執行順序的改變使空載運輸階段總能耗和總節點間距離得以優化。

此外，進一步驗證所提EAPP模型求解方法的有效性。階段1所用PSO的有效性已在文獻[7]中進行了論證，故本文針對階段2使用的NSGA-II，將其與求解多目標優化問題常用的多目標粒子群優化算法(multi-objective PSO，MOPSO)[9]進行對比。

借鑒目前利用PSO解決車間調度以及最短路徑搜索問題常用的粒子編碼方案[10]，將每個粒子表示為(X1,X2,…,X3m,V1,V2,…,V3m)的形式：前3m個元素標記粒子位置信息，取值分別為[0, 1]內的隨機數；后3m個元素記錄粒子在搜索空間各維的速度信息，其取值范圍為[-1, 1]。由于問題可行解是通過粒子空間位置表達的，對任一粒子，其位置信息的前m個元素用于確定運輸任務執行順序：首先將前m個元素的值按照從大到小排列，然后將各元素的值替換為其粒子編碼的位置序號，從而得到運輸任務執行順序。粒子位置信息的中間m個元素從左到右，依次與運輸任務編號1～m相對應，視為確定AGV在各負載運輸階段選擇哪條優化路徑的概率。類似地，粒子位置信息中的最后m個元素從左到右，依次與運輸作業任務執行順序決定的各空載運輸階段相對應，視為確定AGV在各空載運輸階段選擇哪條優化路徑的概率。在各負載/空載運輸階段，可能存在多條最優運輸路徑，這些路徑被選中的概率相等，具體選擇哪條根據輪盤賭法確定。

針對本案例，MOPSO關鍵參數設置如表4所示。

表4 MOPSO參數設置

基于階段1提供的基礎信息，將NSGA-II和MOPSO分別運行5次，發現兩算法得到的Pareto前沿相同，如圖5b所示。解碼對應最低運輸能耗的Pareto解，發現運輸任務的最優執行順序為“2→5→1→3→4”和“1→5→2→3→4”。然而，NSGA-II的平均運行時間(18.816 s)小于MOPSO的(40.675 s)。因此，階段2所用NSGA-II在同時解決運輸任務優化排序和各空載/負載運輸階段最優運輸路徑選擇方面是有效的。

4 結語

針對車間節能生產需求，以單臺單負載AGV為研究對象，建立了面向多運輸任務，以運輸距離和能耗為優化目標的EAPP模型，并提出了一種兩階段模型求解方法。案例研究驗證了模型的有效性，當AGV執行多項運輸任務時，合理安排運輸任務執行順序和規劃運輸路徑能夠提升AGV使用能效。后續將對多負載AGV進行節能路徑規劃研究。