考慮時間容忍度的軌道交通應急接駁公交蓄車點選址研究
何祖勇,郭 茜,吳 剛
(西南交通大學,交通運輸與物流學院,成都 611756)
0 引言
隨著城鎮化的推進、人口的增長及出行需求的增加,城市軌道交通已然成為區域出行的較優選擇,其客運分擔率逐漸增加。但與此同時,它也面臨著巨大的運營壓力,突發事件時有發生。當突發運營中斷時,大量乘客滯留于車站,如疏散不及時,則易發生二次事故。此時,可令附近蓄車點內閑置公交暫行替代,接駁于中斷車站間,以緩解交通壓力。關于應急接駁公交蓄車-分配問題,不少學者已進行了一定的研究。
美國TCRP Report 86 關于公共交通安全一卷[1]中,首次明確指出“當軌道交通發生服務中斷后,在事后救援、恢復階段應充分借助地面公共交通優勢,并將其作為軌道交通應急聯動方式”。Kepaptsoglou 等[2]認為城市軌道交通突發中斷時,公交應提供安全疏散及行程替代服務,首次提出公交網絡“橋接問題”,并設計車輛動態調度初始模型。徐瑞華[3]為有效利用公交運能,提出劃分公交應急責任區、以區為單位組織公交聯動的方法,并根據責任區規模大小分別以蓄車點至車站的最大距離最小和蓄車點數量最少為目標建立蓄車點選址模型。劉靜[4]在考慮車站應急強度基礎上,以加權距離最小為目標,分別以P-中值模型、P-中心模型及最大超額覆蓋模型三種模型來探討蓄車點選址問題。劉爽等[5]將風險分析引入選址問題,利用BP 神經網絡量化車站滯留風險,以平均加權距離最小為目標改進P-中心模型,并對北京海淀區進行實例分析。徐亞楠[6]認為,疏散接駁應采取多蓄車點協同服務方式,即需求站能同時接受多個蓄車點的服務,以系統總接駁時間最短為目標建立的P-中值模型能解決選址及供需點匹配問題。鄧亞娟等[7]以乘客總延誤時間最小為目標,建立反向集合覆蓋模型,并分析不同預設蓄車點數量下總延誤時間的變化情況。姚加林等[8]考慮乘客等車時間影響及公交發車頻率,建立數量有限情況下的公交調度模型,制定公交應急組織方案。王佳冬等[9]以總疏散時間最小和乘客平均延誤最小為目標,建立靈活路徑下的雙目標公交應急調度模型,但未考慮公交運營成本及數量限制。
綜上所述,此前的相關研究多是聚焦效率因素,以時間限制接駁覆蓋范圍,甚至要求公交在規定時間內[4,10]為需求站服務。但在實際中,很難規定確切的接駁限制時間。若時間過短,則易導致蓄車點數量過多,公交資源分散;若時間過長,則乘客延誤成本相應增加。另外,既有研究只是簡單統計了總疏散時間或延誤時間,未充分考慮乘客的時間需求,也忽略了“公交本是一種服務,而服務應以乘客滿意為期望”這一事實。須知,公交并非乘客在軌道交通中斷下的唯一選擇,乘客會根據路徑的出行時間是否超過其可忍受程度而在眾多替代交通方式中進行抉擇[11]。鑒于此,本文從等待時間容忍度出發,以時間懲罰成本最小為目標軟化時間限制約束,間接反映乘客滿意度對應急接駁公交蓄車點選址的影響。
1 軌道交通中斷下應急接駁公交出行等待時間容忍度
1.1 軌道交通中斷下乘客出行方案
1.1.1 乘客分類
當軌道交通某條線路發生運營中斷時,系統內部的乘客可根據原有出行計劃是否受到影響和受影響的程度,分為不受影響乘客、部分受影響乘客及完全受影響乘客(如圖1所示)。
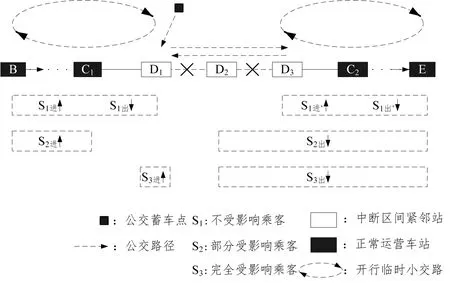
圖1 軌道交通中斷時乘客分類及出行示意圖
(1)不受影響乘客
不受影響乘客,即出行起訖點所在站均位于中斷區間外且同一側的乘客。該類乘客或是在中斷區間上游進出站(S1進↑,S1出↓,含D1站),或是在下游進站(S1進,↑,含D3站),中斷時因軌道交通兩端開行臨時小交路而在下游某站出站(S1出,↓)。總之,無論該區間何時中斷,均未阻礙此類乘客當次出行,乘客原有出行計劃不受影響。
(2)部分受影響乘客
部分受影響乘客,即出行起點所在站位于中斷區間上游非緊鄰站(S2進↑,不含D1站),而訖點所在站位于中斷區間或區間下游(S2出↓,不含D1站)的乘客。該類乘客在中斷前就已進入軌道交通系統并完成當次出行計劃的一部分行程,由于暫時性中斷而無法按時到達計劃訖點所在站,乘客原有出行計劃受到部分影響。
(3)完全受影響乘客
完全受影響乘客,即出行起點所在站為中斷區間上游緊鄰站(S3進↑,只含D1站,本文所定義的需求站之一,同時也是公交折返站),而訖點所在站位于中斷區間或區間下游(S3出↓,不含D1站)的乘客。該類乘客從中斷區間上游緊鄰站進入,但中斷區間涉及該站,無法按原有計劃進入軌道交通系統乘車到達計劃訖點所在站,乘客原有出行計劃完全受到影響。
由上述分類不難發現,在軌道交通中斷后,軌道交通端點站只會產生完全受影響乘客;而對中間站而言,部分受影響乘客及完全受影響乘客均會產生。以下研究將據此展開。
1.1.2 出行方案劃分
受影響乘客需考慮如何前往目的地,有4種出行方案:(1)乘客離開該軌道交通,利用其他方式前往目的地;(2)等待軌道交通恢復后前往;(3)選擇應急接駁公交進行二次換乘,并乘坐軌道交通前往目的地;(4)利用其他方式換乘軌道交通前往目的地。
1.2 應急接駁公交出行等待時間容忍度
1.2.1 等待時間容忍度
時間容忍度源于顧客滿意度[12],而顧客滿意度受多種因素影響。其中,馬云峰等[13]就顧客對配送準時性的滿意度定義了多種時間滿意度函數形式,如線性分布、凸凹分布、嶺型分布、降半哥西分布等。此后,時間滿意度被廣泛應用于物流配送中心[14,15]、供應鏈金融質押物倉庫[16]、電動汽車充電站[17]、鐵路快運站[18]及應急救援設施[19-22]等選址問題中。馬保雨[23]、汪博[24]從時間滿意度出發,分別提出了時間容忍度及時間懲罰成本的概念。
本文定義的時間容忍度,即乘客等待時間容忍度,指的是受影響乘客可以接受的接駁公交從蓄車點到達需求站的時間跨度。在這一跨度內,滿意度最大時的服務為理想服務。超出這一范圍,滿意度將隨到達時間發生改變。此時,乘客對公交服務質量的感知敏感性將高于容忍區。每個需求站的乘客對應一個時間窗[Li,Ui]。其中,Li表示接駁公交理想服務最晚時間,Ui表示公交到達的最晚容忍時間。[Li,Ui]即為需求站i內乘客對應急接駁公交服務的時間容忍度,其值以問卷調查形式獲取。
1.2.2 問卷調查
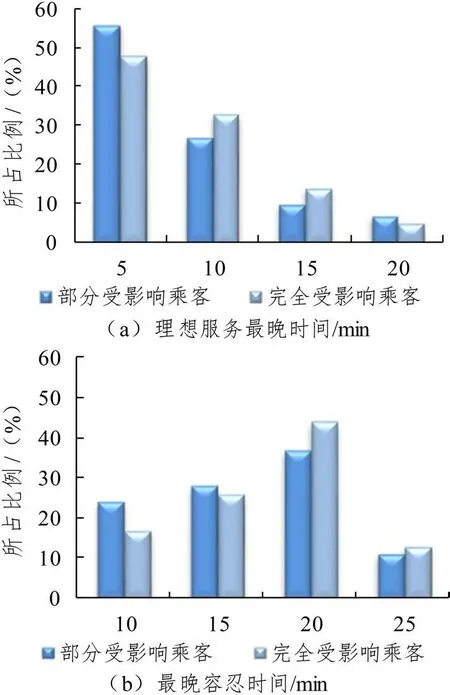
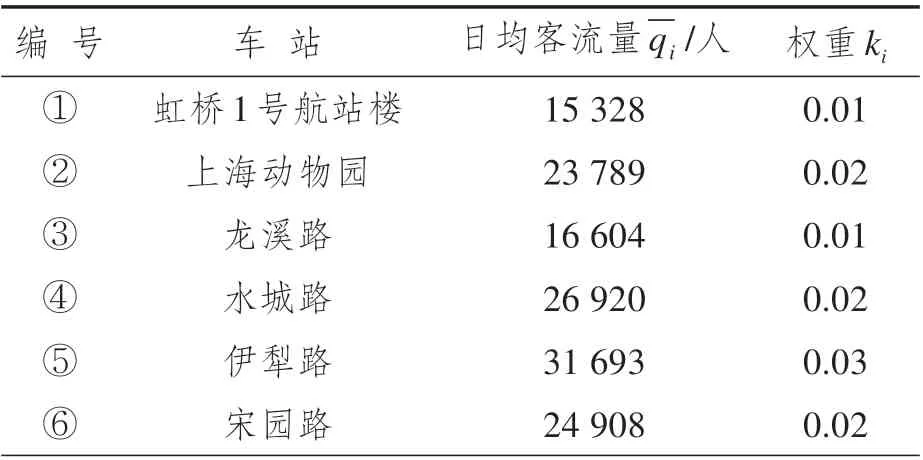
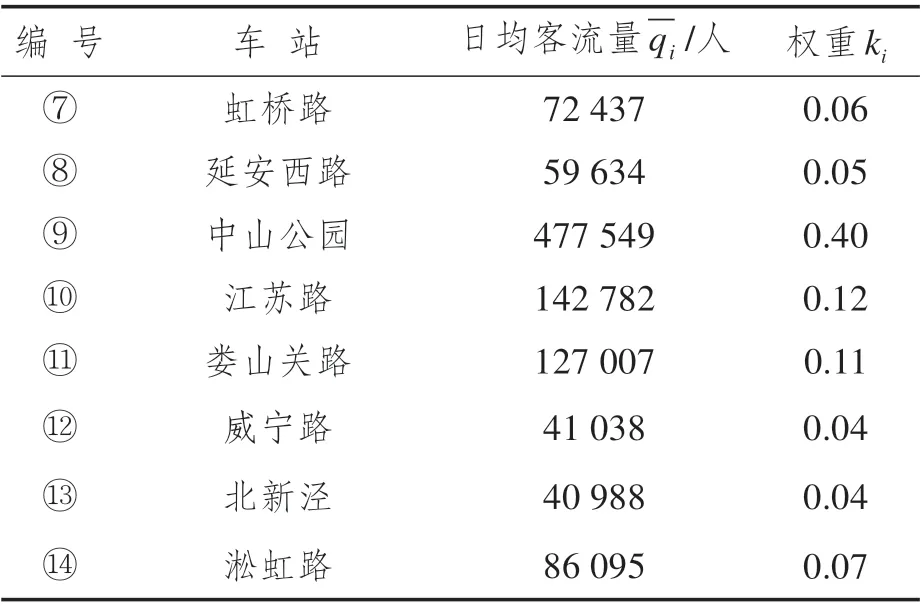
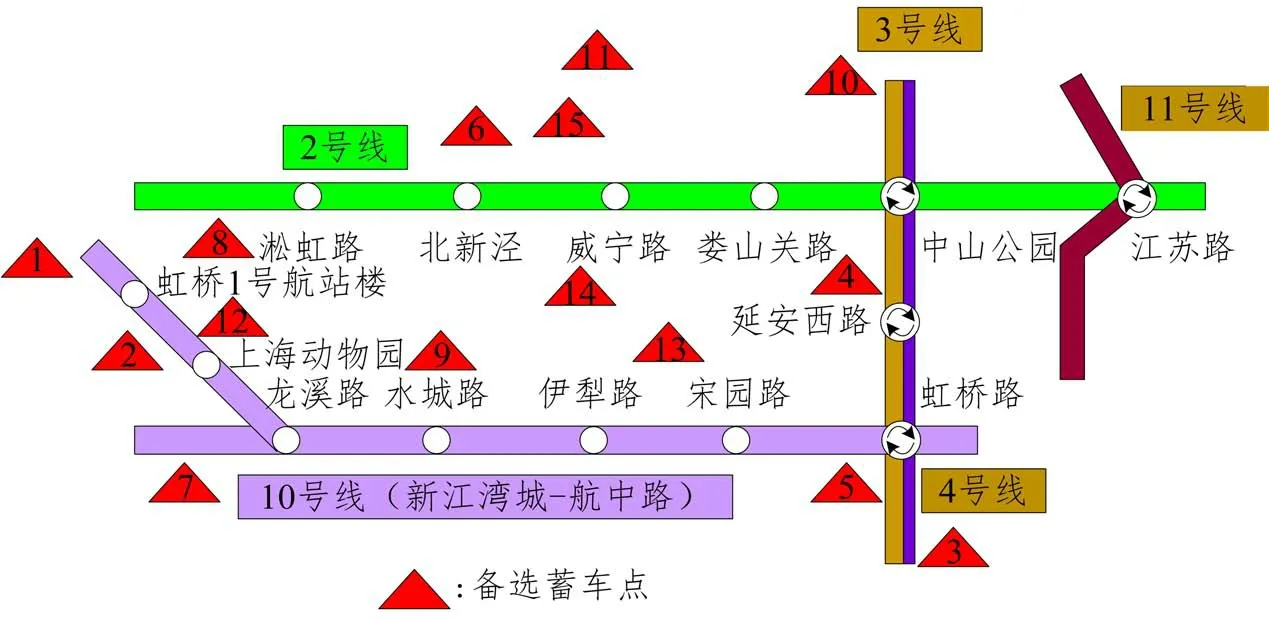
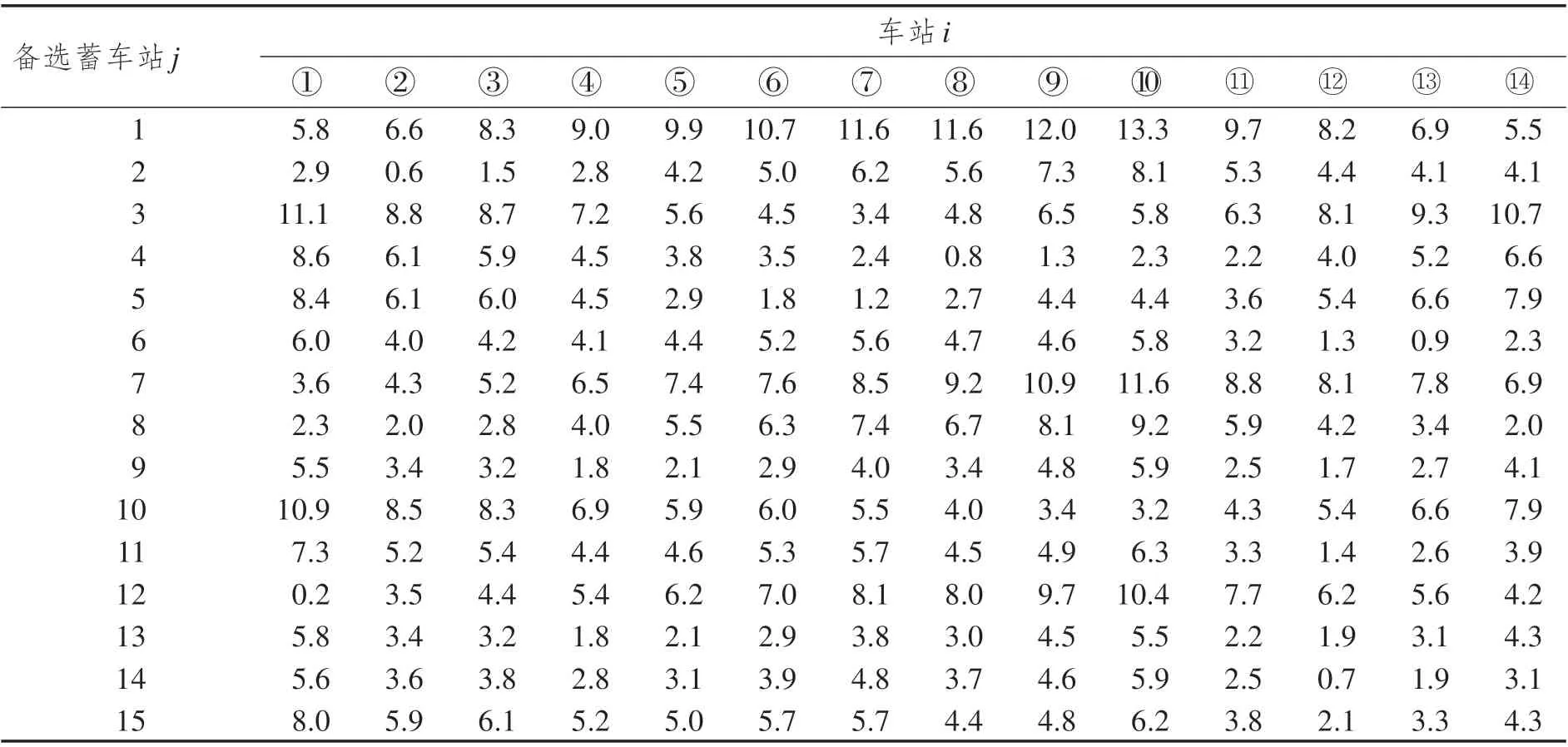
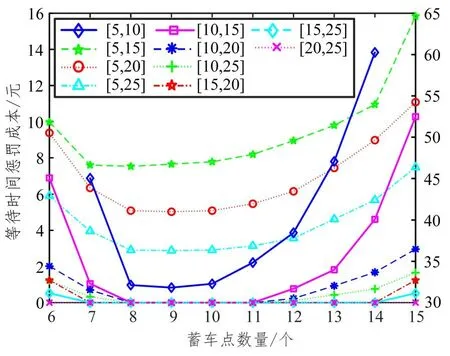
根據乘客分類情況,預設部分受影響及完全受影響兩種中斷情景,分人群展開調查。歷時一周,問卷共收集375 份樣本。回收后,篩選出隨意作答的無效樣本,得有效樣本312份。經數據擬合后發現,在眾多滿意度曲線中,乘客應急接駁公交出行等待時間滿意度函數F(tij)較為符合嶺型分布(如圖2 所示)。tij為應急接駁公交從備選蓄車點j到需求站i的最短接駁時間,min。當tij 圖2 滿意度函數曲線 調查發現,部分受影響乘客較完全受影響乘客對時間的要求更高。因本文案例均為中間站,故綜合考慮兩類乘客的時間容忍度。根據所得分類占比(如圖3所示),以大比例所在時間點作為本文案例的時間懲罰界值(Li= 5min,Ui= 20min,以下單位皆同),定義與滿意度函數相反的時間懲罰成本函數β(tij)。設定各需求站時間窗均為[Li,Ui],時間窗內外賦予不同程度的懲罰。用單位時間懲罰成本Ci表征站點需求強度,其值取車站日均客流權重ki的一百倍,單位:元·分。對Li時間內的服務不予處罰;設置Ui上限時間偏差為σ(此處設為5min),對超出Ui在σ內的部分給予比[Li,Ui]力度更大的懲罰,寓為特殊條件下的無奈之舉,此時滿意度為0,但并不代表完全拒絕,這是符合實際的;超出Ui+σ的部分才被視為拒絕服務,將面臨M的懲罰,M為足夠大的正整數。懲罰函數作為優化目標之一: 圖3 問卷調查結果 軌道交通應急接駁公交蓄車點選址應使公交能在盡可能短的時間內到達需求車站,并且公交服務范圍能覆蓋所有車站。出于應急出行的特殊性,運輸費用在公交選址-調配過程中常被人為忽略,甚至有些地方實行免費公交政策。但在應急接駁公交蓄車點選址決策時,公交維護及管理成本卻不容忽視。為此,應使公交盡可能集中停放,以方便管理及養護。此外,為避免資源浪費,應最小化公交蓄車點數。 城市軌道交通突發事件并不頻發,專門為應急接駁車輛設立蓄車點不現實,但公交系統通常會預留車輛用于高峰運能補充及故障車輛替代[3]。所以,蓄車點選址應在已有設施內進行選擇而非新建,具體選擇范圍可包括:公交樞紐站、附近公共場所(如學校、醫院、公園等)、部分公交始末站及停車場。 2.3.1 符號說明 模型中使用的符合如表1所示。 表1 符號含義 2.3.2 數學模型 目標函數Z1表示整個責任區內應急接駁公交蓄車點數量最少,也可認為是各站均為單位成本下的公交維護及管理成本最低;目標函數Z2表示乘客應急接駁公交等待時間懲罰成本最低;公式(3)表示服務于責任區內需求站的蓄車點所能提供的公交車總數不少于路網所需儲備公交車數下限;公式(4)表示每個需求站的公交數量需求都能得到滿足;公式(5)和公式(6)表示只有在建立蓄車點j的情況下才能向需求站i提供公交接駁服務,且蓄車點一旦建立則至少為一個需求站服務;公式(7)為決策變量0-1約束。 其中: 式中:Qr為列車平均載客量;Tr為應急接駁公交啟動閾值,min;ub為公交車輛在責任區內同一線路任意多個相連站點中斷情境下疏散客流的平均周轉時間,與責任區規模及站點安排有關,min;n為責任區內軌道交通車站數量;Qb為公交額定載客量;Ub為規定的公交疏散時間上限,min;tr為列車臨時開行小交路的運行間隔,一般較正常行駛時大,min;nr為受影響車站數量;-vr為列車延誤傳播速度,即列車在運行延誤情況下,引起后效延誤的平均傳播速度,km·h-1;l為軌道交通平均站間距,km;-qi為需求站i日均客流量;ti為需求站i所在軌道交通線路單日運營時間,h;Int(*)表示對*向上取整。 本文構建的模型為雙目標0-1 規劃模型,求解具有一定難度。加之案例中約束及變量較多,而多目標優化算法的有效性又較難保證。為確保結果準確性和滿足精度要求,首先,選用ε-約束法對模型進行處理。ε-約束法是將某一目標函數轉化為約束條件,并給予期望的ε值,從而將多目標問題轉化為單目標問題,最后得到ε不同賦值情況下的Pareto 解集。由于目標函數Z1得到的是有限離散集,ε的可能取值易列舉,故而將其轉化為約束。通過變更ε的值,對目標函數Z2進行優化求解,最終可獲得由所有Pareto 最優解對應目標函數值構成的精確Pareto 前沿。為更好地反映時間容忍度對選址數量的影響,現將傳統ε-約束法進行適當修改,修改后的轉化形式如下: 此形式下,x*(ε)∈X,f2(ε)=Z2(x*(ε)),f1(ε)=Z1(x*(ε))≤ε。不難證明,對任意x∈Ps,存在一個ε,使得x=x*(ε)。 然后,采用Lingo11.0 在配置為Intel(R)Core(TM)i5-6300HQ CPU @ 2.30GHz,運行內存為4GB,操作系統為WIN10 64bit 的計算機上,對轉化后的單目標模型進行求解。包括因變更ε取值所產生的輸入時間,共耗時67s。 表2 長寧區車站2018年12月日均客流量權重 續表2 表3 備選蓄車點可供公交車數 圖4 責任區所含車站及蓄車點分布圖 表4 備選蓄車點與需求車站間公交最短可行距離單位:km 案例中,滿足所有約束條件的ε取值范圍為[6,15],且ε為整數。圖5 為修改后的ε-約束法在該范圍下經Lingo 軟件求解得到的目標函數Z2的所有最優值。因兩個目標函數均取最小值,精確Pareto 前沿應為由離散點構成的上凹遞減曲線,圖中表示為左側黑色趨勢線所包含的四個點,對應具體蓄車-分配方案如表5 所示。例如,在方案1 中,蓄車點數量為6,2?②③④表示對應編號為2的備選蓄車點被確定為蓄車點,在軌道交通線路發生中斷時可服務于編號為②、③、④的軌道交通車站,其余類似。不同方案中,蓄車點2 的固定服務對象為車站②、③,蓄車點4 的固定服務對象為車站⑧、⑨、⑩、?,蓄車點5 的固定服務對象為車站⑦,蓄車點6的固定服務對象為車站?。車站?在方案1 中被蓄車點6 服務,而在其他方案中均被與其最近的蓄車點8 服務。可見在考慮乘客時間容忍度后,蓄車點并不總是服務于最近的需求站,并且一般無法獲得多蓄車點協同服務于同一需求站的結果,這是由時間限制決定的。 圖5 ε -約束法處理后的計算結果 表5 蓄車-分配方案 為反映時間懲罰成本函數中Li和Ui對結果的影響,參考1.2.2 節中調查的結果,設計時間窗[Li,Ui]分別為[5,10]、[5,15]、[5,20]、[5,25]、[10,15]、[10,20]、[10,25]、[15,20]、[15,25]、[20,25]等10 個序列的對比實驗,得到不同時間容忍度下目標函數曲線的變化趨勢如圖6所示。 圖6 目標函數值隨時間容忍度變化圖 圖6 中,序列[5,10]的縱坐標對應右側值,其余序列的縱坐標對應左側值。分析各曲線Pareto 前沿(左側離散點構成的上凹遞減部分)后發現,由非支配解構成的Pareto 最優解集中解的個數依序列順次大體呈遞減趨勢。在序列[5,10]中,時間懲罰成本明顯較高,滿足所有約束條件下的目標函數Z1的原有取值范圍由[6,15]縮小至[7,14]。這意味著當蓄車點數量為6 或15 時,均存在蓄車點提供的公交接駁服務遭到乘客拒絕的現象。若繼續降低[Li,Ui],則該現象更為突出。即便蓄車點數量維持在7~14 之間,仍有乘客對部分蓄車點提供的公交接駁服務的滿意度為0,只是由于條件限制而迫于接受。而在序列[20,25]中,各方案的時間懲罰成本均為0,非支配解集中只含蓄車點數量為6 時對應的解,意味著這些乘客對接駁時間足夠的“寬容”,可在最大范圍內減少蓄車點數量。但就調查結果來看,無論是部分受影響乘客還是完全受影響乘客,在該序列的占比均不高。 本文從軌道交通應急接駁公交蓄車點選址問題出發,充分考慮公交公司管理維護便利性和乘客等待時間容忍度,建立了以蓄車點數量最少和時間懲罰成本最低為目標的雙目標選址-分配模型。該模型能避免接駁限制時間難以確定的問題,并在一定程度上反映乘客等待時間要求對選址的影響。研究發現,在考慮時間容忍度后,蓄車點并非總是服務其最近的需求站。當時間容忍度降低至一定程度后,乘客對部分蓄車點所提供的公交接駁服務滿意度為零,甚至直接拒絕服務;而當時間容忍度超過界值后,其對選址決策的影響顯著降低,此時可最大限度減少蓄車點數量。 在時間窗設置中,有別于其他研究普遍采用均勻隨機生成的方法,本文認為各需求站時間窗一致,主要是出于對各站乘客出行公平性的考量。但在實際中,可能會因站點重要性、客流量等因素而采用不同的時間窗。文中對乘客采取此番劃分,緣于軌道交通端點站只產生完全受影響乘客,所以端點站只需考慮完全受影響乘客的時間容忍度;對中間站而言,部分受影響乘客及完全受影響乘客均會產生,所以需綜合考慮。一般來說,端點站重要性不及中間站,在選址決策時,應優先考慮中間站后考慮端點站,或稱中斷站接駁優先級,后續可就此進行研究。另外,還可將選址與接駁線路設計相聯系。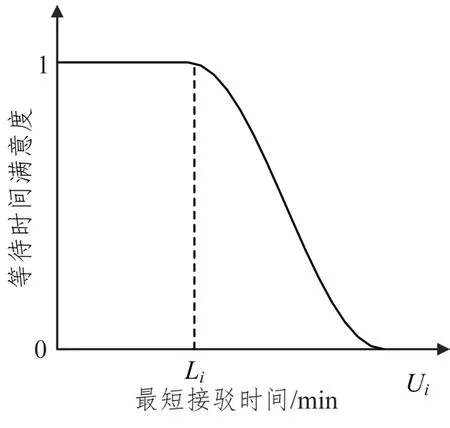
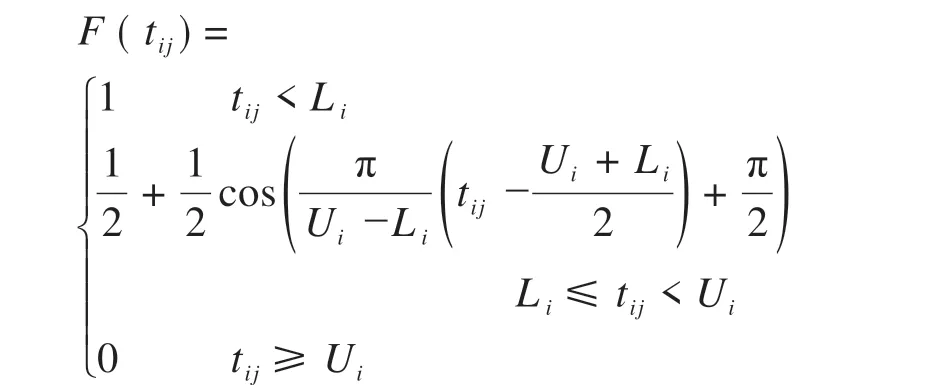
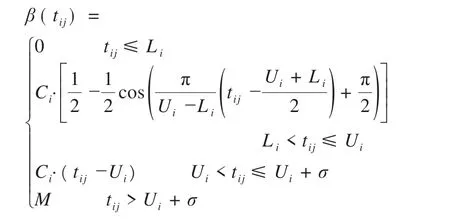
2 考慮時間容忍度的應急接駁公交蓄車點選址模型
2.1 選址原則
2.2 選址范圍
2.3 選址模型構建

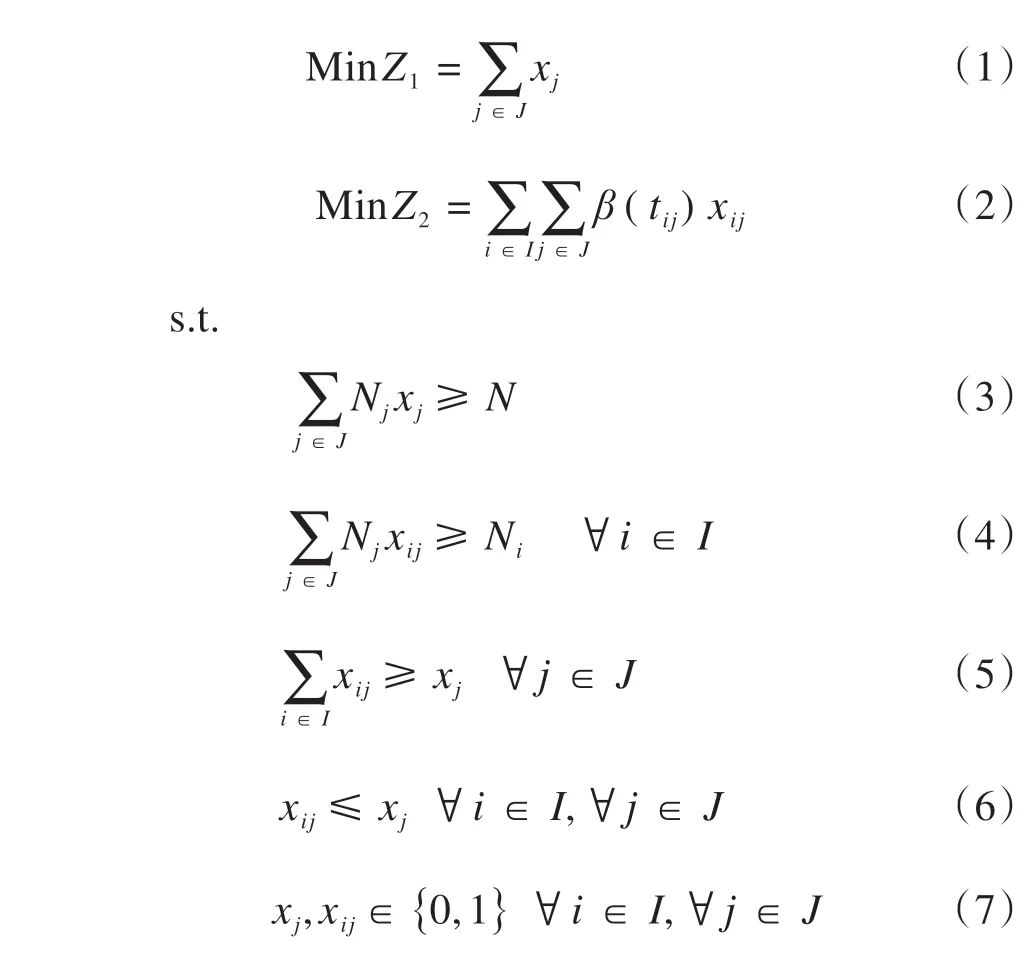
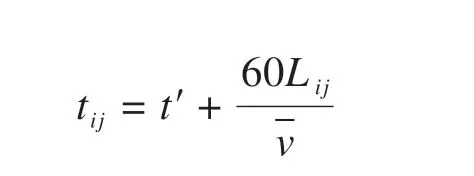

2.4 選址模型求解

3 案例分析
3.1 案例描述


3.2 求解結果




3.3 靈敏度分析
4 結束語

