RNS 在彩色圖像水印中的應用*
陳丁睿 佟國香
(上海理工大學 上海 200093)
1 引言
近年來,數字技術發展迅速,伴隨著網絡的發展,數字產業的快速發展,以及數字圖像所具有的廣泛實用性和功能性等特點,數字圖像已成為應用最廣泛的一種數字信息。但隨之而來的是多媒體數據的版權保護問題,而數字水印在版權保護方面起到了重要的作用。數字水印在近年來也發展了許多,在科研人員中也出現了許多杰出的成果[1~5]。文獻[12]選擇對圖像進行三級離散小波變換,再對變換后得到的低頻子帶進行奇異值分解。在強魯棒性的研究上面,文獻[13]提出了一種具有多方向,多尺度特征的二維圖像分析算法,但是不足的是,圖像邊緣會出現偽Gibbs 失真現象。文獻[14]提出了一種基于局部特征的魯棒盲水印算法,算法魯棒性強,提取圖像的特征點是其算法的主要內容,其算法缺點是視覺質量的下降。因此,圖像水印技術中最難的一個技術點就是在保證圖像質量的前提下,盡可能平衡不可見性和魯棒性。
本文針對上述問題提出了一種對原始水印圖像進行二重加密的方法。算法利用基于中國剩余定理(CRT)的RNS余數系統進行水印的加密,再結合Arnold 置亂使得加密的圖像具備二次加密性和良好的隨機性。此外,基于DCT域的數字圖像數字水印算法,將立足于基于人眼視覺系統,將不同基色的水印分量嵌入到DCT 的中頻系數當中。本文提出的RNS加密算法運算簡單,使得水印具有良好的不可見性,相比傳統的混沌系統加密,RNS 的加密速度更快。
2 相關理論分析
2.1 Arnold置亂
Arnold 置亂的原理是利用置換矩陣,將矩陣中的像素點重新排列,從而達到加密的效果[15]。
二維Arnold置亂的公式為
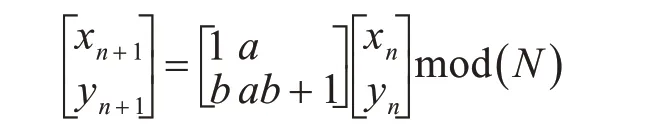
xn,yn是原始圖像矩陣中的像素點的初始位置。xn+1,yn+1是變換后的新位置。經過多次置亂后,圖像會失去本來的面目。
實驗中發現,Arnold 置亂沒有密鑰參與,且具有周期性,且這種置亂只是像素位置的變換,圖像的統計信息無法加密,安全系數并不理想。因此,我們需要利用RNS進行二次加密。
2.2 RNS余數系統
RNS是一個非權重數值表征系統,RNS不同于十進制、二進制那樣有權位的數制,它的數值表示和算數運算都是用余數進行的,余數運算是一種并行運算,不需要進位,具有高精度[11]。余數系統可表現為如下形式。
{m1,m2…mn}為一組兩兩互質的正整數,整數X由它對該余數基的余數向量{x1,x2…xn}來表示,其中xi=Xmodmi,?i∈{1,2…n},寫作xi=X mi由式(1)可以確定X的值:

一個完整的余數系統至少應該包含三個部分:余數約化、余數運算、余/二后向轉換(R/B 轉換)。余數約化的目的是將有位權數值表示轉化為余數表示,余數運算包括算數四則運算和其他的必要運算,R/B 轉換的作用是將各種余數運算的最終結果從余數制表示轉換成二進制表示[9]。
R/B 轉換是余數系統的重要內容。目前,對于普通余數基的R/B 轉換,主要有以下兩種方法:混合基轉換和中國剩余定理(CRT)[10],本文主要的R/B 實現也是基于CRT 及其變形來處理。文獻[6]對CRT 進行變形,得到了上述定理的三個推論CRT-I,CRT-II 和CRT-III,本文主要利用CRT-I 作為RNS的后向轉換算法進行水印的提取。
CRT-I計算X可以由式(3)確定:

將上述內容帶入式(3)可以求得R/B的后向轉換算法:

3 水印的嵌入和提取
3.1 水印的嵌入方案
Step1:首先,將水印圖像進行Arnold 置亂得到置亂后的水印圖像,實現初步加密。
Step2:將加密后的圖像按照余數基進行取余,得到三通道的RNS余數塊,實現二次加密。
Step3:對載體圖像進行RGB 分解得到RGB 灰度圖像,將RGB 灰度圖像按N*N 的數據塊進行DCT變換,再將三通道的RNS數據塊按照合適的嵌入強度a 分別嵌入到RGB 灰度圖像的DCT 中頻變換域數據塊中:
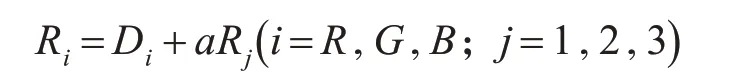
a 為嵌入強度,D 為DCT 變換后的基色圖像矩陣,Rj為RNS 余數塊,Ri為嵌入水印后的DCT 變換圖像矩陣。
Step4:再分別對嵌入水印后的圖像矩陣按N*N 的數據塊進行DCT 反變換得到加密后的RGB灰度圖像,再將三通道的分量合成得到加密后的彩色圖像。圖1為水印嵌入的流程圖。

圖1 水印嵌入流程圖
3.2 水印的提取方案
Step1:將嵌入水印的彩色圖像按RGB 分量進行分解,獲得三通道的灰度圖像。
Step2:將三通道的灰度圖像按照N*N 的數據塊進行DCT變換,并且與未嵌入水印的彩色圖像的RGB 三通道的DCT 變換矩陣作差獲得嵌入的三通道水印數值。
Step3:按照嵌入強度a 對水印數值進行縮放,獲得三通道的RNS余數塊,再利用R/B的后向轉換算法獲得初步加密的水印圖像,最后對上述圖像進行Arnold反置亂,獲得水印圖像。
4 實驗仿真和結果分析
本實驗用Matlab 來對圖像進行水印的加密和嵌入。載體圖像選取一幅分辨率為256*256 的標準Lena 彩色圖像,水印圖像為32*32 的灰度圖像,DCT 變換的數據塊選擇8*8 數據塊,嵌入強度a 取3.5。
峰值信噪比PSNR 用來評價算法的不可見性,PSNR 的值越大,說明水印圖像對原始載體圖像的改變越小,算法的不可見性越好,彩色圖像的PSNR計算公式定義如下:

NC 歸一化相關性表示提取出的水印圖像與原始水印圖像的相似程度,它的值越大,表明算法的魯棒性越好。在此基礎上,還需要通過各種常見攻擊來深入測試水印的魯棒性:在嵌入水印之后,對載體圖像進行裁剪、JPEG 壓縮、旋轉、添加噪聲以及均值濾波、中值濾波等多種常見的水印攻擊。圖2 是RGB 原始載體圖像和原始水印圖像;圖3 是含水印的RGB 載體圖像和未受攻擊情況下提取的水印圖像;圖4 是旋轉45°后的載體圖像和提取的水印圖像;圖5 是添加高斯噪聲0.1 后的RGB 載體圖像和提取的水印圖像。

圖2 原始圖像和水印

圖3 未受攻擊的載體圖像和水印

圖4 旋轉45°的載體圖像和水印

圖5 高斯噪聲0.1的載體圖像和水印
表1 是本文算法與和另一文獻中結合傅里葉全息加密技術和非抽樣變換的的彩色圖像水印算法的性能比較,顯然,本文的算法效果更優。

表1 算法抗攻擊性能比較
在RNS中,通過對該系統下的每個分量進行加減法和乘法操作,可以實現大數相加減和乘法運算。RNS中的各個分量在運算時不需要進位,這使得算法的并行度得到極大的提高。本文的算法將余數系統分為RGB 三通道進行并行計算,并且與文獻[8]提供的算法進行時間上的比較,實驗均采用256*256 的國際標準測試圖像,如圖6 所示。可見,RNS 算法不僅具有良好的加密效果,還能實現高速的計算。

圖6 算法速度性能比較
5 結語
本文結合基于中國剩余定理(CRT)的RNS 余數系統和Arnold置亂,提出了一種適用于彩色圖像的數字水印嵌入算法,試驗結果表明,對于普通的幾何攻擊或噪聲攻擊,該算法具有較強的魯棒性,算法速度快。若采用FPGA 硬件平臺,可以設計RNS 復用處理器,實現算法的可重構特性,并通過合理的調度實現數據級并行和指令集并行,充分挖掘數據的并行度,加快運算速度,有很強的實用性。

