基于注塑機螺桿位置與壓力曲線的注射成型過程監測方法

0 引 言

注射成型是塑料熔體在溫度、壓力作用下材料狀態發生復雜變化的過程，成型過程與制品質量存在非線性、強耦合和時變性的關系，導致制品成型質量較預測困難

。隨著傳感技術與計算機嵌入系統的發展，注塑機或模具內的傳感器在成型過程中記錄了大量的過程曲線數據，包括螺桿位置、速度、溫度和壓力等，這些數據蘊含了注射成型過程質量信息

。由于曲線數據維度高，難以直接通過這些曲線數據獲取足夠的注射成型過程信息。近年來，人工智能方法促進了數據降維以及模式識別的發展，使從高維度數據建立成型過程質量關系成為可能。

以前注射成型過程監控主要采用主成分分析法（principal component analysis，PCA），在假定變量獨立分布且服從正態分布條件下，將多個變量通過線性變換得到重要變量，去除原始數據的冗余信息

。主成分分析法僅適用于連續工業生產過程的二維數據，而塑料熔體注射成型是典型間歇性生產過程，一般采用多向主成分分析法將曲線變量、時間和批次構成的三維結構展開為二維結構

。如YI X H等

通過多向主成分分析法分析了保壓、注射2個階段的螺桿位置和壓力曲線，并開發塑料熔體注射成型的過程檢測系統。但是主成分分析法和多向主成分分析法本質上都是一種線性變換，它們要求變量之間相互獨立且服從正態分布的假設與塑料熔體注射成型過程非線性、強耦合的實際情況不相符。YUN Z等

將統計分析法（statistic pattern，SP）引入注射成型過程監控，通過提取曲線數據的統計量，將數據從930維降至26維后再使用主成分分析法建立監控模型，解決了上述問題，但由于統計分析法僅考慮變量之間的整體統計因子，沒有考慮實際變量參數之間的聯系，丟失了較多的數據信息。

現分別使用主成分分析法和3種非線性法，即統計分析法、拉普拉斯映射（laplace eigenmaps，LE）法、擴散系數圖（diffusion maps，DM）法對塑料熔體注射成型過程進行數據降維和特征提取，然后通過神經網絡模型建立特征數據與制品成型質量之間的關系模型，研究塑料熔體注射成型過程的監控技術。

1 注塑機曲線的降維與監測模型

注塑機曲線的降維與監測模型如圖1所示，首先通過注塑機獲得螺桿的壓力和位置曲線的原始數據，進行預處理后分別采用4種方法降維后輸入神經網絡，完成塑料原料監測、模具溫度監測和成型制品質量預測的功能。

主持人：近日，習近平總書記、李克強總理、多部委負責人頻頻為民營企業發聲，支持民營經濟發展，一系列針對性舉措密集出臺，這釋放了什么信號？在我國經濟步入高質量發展軌道的背景下，民營企業面臨著哪些困難和挑戰？

1.1 數據采集與預處理

注射成型過程的主要控制變量包括熔體溫度、注射位置、注射速度和注射壓力等，因此理論上需要采集熔體的溫度曲線、螺桿的位置、速度和壓力曲線。考慮注塑機的溫度傳感器安裝在料筒外壁，塑料熔體熱導率低導致測量溫度數據滯后性較大，溫度曲線不是一種實時監測曲線。同時塑料熔體的溫度、壓力和體積必須滿足PVT方程，因此溫度曲線的信息可以通過螺桿的位置（體積）和壓力曲線間接反映，此外螺桿的速度是其位置的一階導數，注塑機監測曲線選擇螺桿位置和壓力曲線。

為了避免監測變量曲線范圍差異對后續分析的影響，需要對數據進行歸一化預處理。數據歸一化是數據建模前重要的數據處理步驟，包括樣本尺度歸一化、逐樣本的均值相減和特征標準化3種。逐樣本的均值相減主要應用于穩定性的數據集中，即數據每個維度間的統計性質是一樣的情況，而注射成型過程中螺桿位置和壓力在不同時刻信息不同，此方法不適用。特征標準化是指對數據的每一維進行均值化和方差相等化，常用的數據標準化方法有：Z標準化、最大值-最小值標準化、Log函數標準化等。根據數據特征，采用Z標準化方法，基于統計理論的偏差標準化，使經過處理的數據符合標準正態分布，即均值為0，標準差為1，處理步驟如下。

（1）中心化處理，即去均值，消除自身變異、數值大小帶來的影響，即

式中：

——原始螺桿位置或壓力；

——相應中心化處理后的數據；

——曲線采樣點數；

——采樣數值均值。

（2）無量綱化處理，即

式中：

——無量綱化處理后的數據；

——采樣數值均方根誤差。

通過旅行，我學到了很多地理和歷史知識。為了與人交流，我學會了英語、西班牙語和越南語。在越南待了7年之后，可以說我對這個國家的了解要甚于我對自己的了解。

1.2 數據降維方法

質量預測模型最后輸出一個具體的數字，而不是類別，即如果故障監測是一個離散的輸出，質量預測就是一個連續輸出。模型的設計層數確定、隱藏神經單元與故障監測一致，與故障監測最后的Softmax分類器不同，質量預測采用的是擬合器。

（1）主成分分析法。主成分分析法是將高維度數據空間通過線性變換投影到低維度主成分空間，選出較少個數的重要變量的多元統計分析方法

。它去除了原始數據中的冗余信息，是有效的數據壓縮和信息提取的方法。主成分分析法適用于二維數據矩陣

(

×

)，其中

是數據樣本的個數，

是數據維度，得到得分向量、負載向量、特征值，即

經 FPD檢測器檢測，發現樣品圖譜中分別含有出峰時間相互對應的 3個峰，通過與有機磷類農藥標樣檢測圖譜的出峰時間進行比對，確定檢出的農藥組分分別為敵敵畏、氧化樂果、甲基對硫磷。經ECD檢測器檢測，發現樣品圖譜中含有出峰時間相對應的 4個峰，通過與有機氯類農藥標樣檢測圖譜的出峰時間進行比對，確定檢出的農藥組分分別是乙烯菌核利、聯苯菊酯、氯氰菊酯、氰戊菊酯。

(2)次生地質災害嚴重，道路、電力、通訊全面受阻，救援生命線修復艱難。云南地震帶與河谷疊合，地震區多為高山峽谷區，地震常造成巨型次生地質災害，道路打通極為困難。余震、降雨又會誘發新的地質災害，造成交通再次阻斷，傷員轉運困難，滯留在重災區轉運不出去。生活物資因地震被毀，而救援物資又難以進入災區，造成交通大堵塞，大量救災物資停留在重災區10 km左右，而災區物資又十分缺乏，且救援的核心之一醫護人員難以第一時間到達災區。

式中：

得分向量；

——負載向量。

此外，南充市旅游景點交通通達性呈現一定的規律特征：城市景區通達性優于鄉鎮景區通達性，平地景區通達性普遍優于山丘景區通達性，5A景區通達性明顯優于4A及其以下等級景區通達性，原有景區通達性優于新建景區通達性。區域經濟發展水平以及景點的知名度對旅游景點的整體交通網絡可達性指數影響較大。

也因為漂亮，女人無法辜負這般人才。于是，她的所想所慮全都集中在了維持這份漂亮的穿著打扮上面。這么一來，小時候的書是很難讀得好的，稍大一點又容易情竇早開，墜入男女的情感糾葛之中。而正是早戀早婚，其實還毫無社會與人生的經驗，往往導致婚后不幸，命運多蹇。

式中：

——熱核的寬度，其取值與鄰域

相適應。

（2）統計分析法。統計分析法是一種利用數據統計信息完成對數據降維再現的一種信息處理、壓縮和提取方法

。統計變量包括一階統計量（平均值

）、二階統計量（方差

）、三階統計量（偏度

）、四階統計量（峰度

）等，定義如下：

（3）拉普拉斯映射法。拉普拉斯映射法算法尋找一個低維度數據來保留流形數據的局部性質

。通過相鄰2點之間的距離實現數據的低維度再現，通過權重的方式實現數據點之間的距離和

個近鄰被最小化，即離得越近的點對于代價函數影響越大。使用稀疏光譜理論，將代價函數定義為特征問題，算法分為以下幾步。

1）構建鄰接圖

，可采用近鄰

法或

近鄰法，即采用

近鄰法。

2）定義近鄰權矩陣

，可采用熱核方式或簡單連接方式，現采用熱核方式，即若

x

和

x

相鄰，那么

我國古代的藏書機構在不同時期，分別被稱為“府”“觀”“臺”“閣”“殿”“院”“堂”“齋”“樓”等。我國有文字記載的最早的藏書機構是“盟府”和“藏室”。據《左傳·襄公十一年》記載：“國之典也，藏在盟府。”是指東周時期各諸侯國建立盟府，用以掌管、儲存盟約文書和典籍等。《史記·老子韓非列傳》記載，老子“周守藏室之史也”。老子曾擔任管理“藏室”的官吏。由此證明，“盟府”和“藏室”是中國歷史古代文字記載的最早的藏書機構。

2）計算數據圖，權重的連接使用高斯核函數。

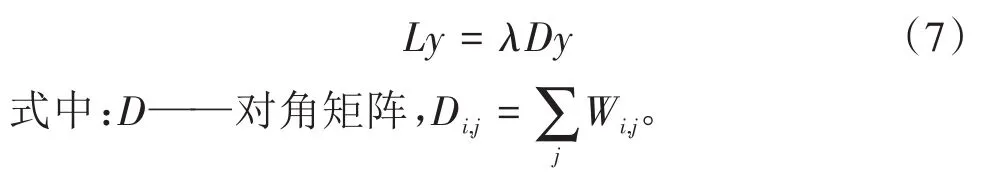
的最小

+1個特征值對應的特征向量

，

，…，

μ

構成了低維嵌入結果

=[

，

，…

μ

]

。該方法將降維和特征提取問題轉化為對矩陣特征值和特征向量的求解，過程簡單，無需迭代，因此計算量和計算時間減少。

（4）擴散系數圖法。擴散系數圖法同拉普拉斯映射法一樣屬于非線性降維方法，都是通過找到其隱藏的低維度空間數據結構，達到降維的目的。不同于拉普拉斯映射法基于鄰近圖的稀疏光譜分析，擴散系數圖法是在保留局部性質的條件下基于分散距離的全光譜分析的降維方法

。擴散系數圖法特征降維步驟如下。

1）進行下式的數據規范化，保證數據落在（0,1）。

朱俊玲《中國戲曲學院京劇經典劇目的傳承與創新研究初探》[10]一文對中國戲曲學院對京劇經典劇目的傳承與創新進行了簡單總結：（1）基本保持原型，改動甚微的經典劇目；（2）融入新時代特色，改動較大的傳統劇目；（3）貼近現代生活，完全新創的劇目。以上三類也是目前京劇劇目的創作現狀。對于經典劇目與新創劇目，筆者就徐州民眾對于京劇現代劇與傳統劇的喜好進行了調查，有效問卷198份。其中有149位民眾選擇傳統京劇，可見人們更偏愛經典故事。

3）構建拉普拉斯特征矩陣

=

-

，最小化特征映射誤差，相當于計算下式中的最小特征向量。

式中：

——高斯方差。

3）計算矩陣

的行向量之和

。

定義了前向轉移概率矩陣的Markov矩陣，表示在數據集中的一個數據點經一次轉移至另一個數據點的過程。

式中：

P

——前向

次迭代的矩陣，可以通過其行向量之和定義擴散距離。

式中：

(

x

x

)——擴散距離；

(

x

)

——表示將更多的權重歸因于高密度圖的部分。

4）使用譜理論得到保留了擴散距離的低維度再現數據

。

由于圖是全部鏈接的，最大特征值是平凡的，為1，被舍棄。再現數據

是

分主特征向量，即

={

,

,...,

λ

v

}。

1.3 故障監測與質量預測模型

可以通過不同降維方法提取數據特征以實現故障監測和質量預測，常用的有神經網絡和支持向量機等。神經網絡理論發展成熟

，支持向量機解決了神經網絡存在的收斂速度慢、存在局部最小點等問題

，支持向量機在分類問題上具有優勢，考慮存在分類和擬合兩大方面，故采用神經網絡作為建模方法。

律師稱楊偉東被警方帶走，并不能以此就認定其有罪。但他分析，消息爆出后阿里巴巴很快確認，并且應對有序，“當事人可能都不知道，但該知道的人或許早已知道，阿里內部很可能已經做了初步調查并掌握了一定的證據。而且楊偉東剛好在輪值結束后出事，要么是阿里真的非常幸運，要么是一切都在安排之中。”

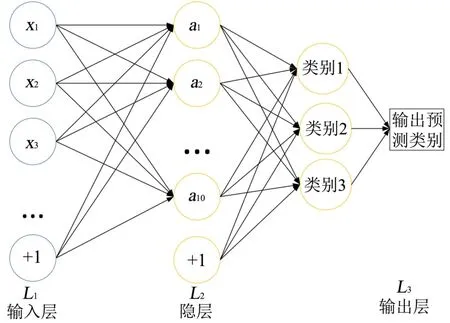
故障監測的主要目的是實現對原材料和模具溫度的故障診斷，采用分類器進行監測。神經網絡層數越多，神經元數量越多，則訓練精度越高，但是同時網絡的泛化能力下降。為了取得較好的結果，根據應用場景，輸入向量為降維后的數據，在20維左右，輸出類型為3類。根據Kolmogorov定理，可采用三層神經網絡結構。根據試驗，發現神經元數量穩定在10個左右，分類函數選用Softmax分類器。故障監測的模型如圖2所示。

注塑機螺桿的壓力和速度在每一模內隨時間變化，數據在時間和批次展開后維度高，直接計算成本大。降維處理是在盡可能保留原始信息的情況下，通過找出高維度的數據中占重要因素的點或者發現變量之間隱藏的關系，用較低維度的數據再現原始數據

。相比原始數據，降維后的數據不僅維數降低，而且更有可能反映原始數據不能體現的隱藏數據關系。現重點分析1種線性和3種非線性方法對數據進行降維。

2 試驗設計

注射成型過程可以分為塑化、注射、保壓和冷卻4個階段，這4個階段決定了最終制品的成型質量，由于塑化的結果可以在注射和保壓的過程控制曲線中體現，可以減去塑化階段。模具溫度的分布和變化將影響熔體的流動阻力，因此冷卻階段的變化也可以體現在注射和保壓階段的控制曲線中。依據以上2點，試驗的采樣為注射和保壓階段的螺桿位移和壓力曲線。試驗采用900 kN伺服液壓注塑機，螺桿位移通過光柵尺測量，壓力采用液壓系統壓力，采樣周期為3 ms。塑料材料為聚丙烯PPHT03，試驗制品采用 68 mm×60 mm×41 mm的盒形件，平均壁厚為2 mm，以制品的成型質量作為評價指標。

在實際注射過程中，即使考慮工藝參數不變，制品的成型質量也會由于環境或工況因素產生波動，設計了模具冷卻溫度和是否為回用料（制品經過回收粉碎后獲得的原材料）作為工況變化的變量，并通過重復試驗減少非控制變量對成型制品質量結果產生的影響，試驗條件如表1所示。

故障監測模型采用均方差MSE和百分誤差

%進行評價。MSE越小，表明模型分類越好，0表示沒有誤差。

%表明樣本被錯誤分類的比例，0表示分類完全正確，100表示全部錯誤。質量預測模型采用MSE和回歸系數

進行評價。

表示測量輸出值和目標值之間的相關關系，

值為1表明相關性較高，0表示隨機關系。

3 結果與討論

3.1 故障監測結果與討論

基于控制曲線判斷制品原材料、模具溫度是否屬于正常類別，達到故障監測的目的。實際生產中，原材料雖然由加料處直接控制，但是原材料與回用料之間并沒有嚴格的區分，容易造成混料，這樣通過檢測制品的生產過程曲線來判斷原材料的種類以保證生產的正常進行很有必要。試驗中采用原材料為1，回用料為0進行分類，試驗結果如表2所示。

由表2可以看出：盡管相比于原始數據訓練的均方差和百分誤差，降維后的數據在驗證集、測試集上都有較大的改善，LE和DM方法在測試集上百分誤差為0。DM在訓練、驗證、測試時百分誤差都為0，分類達到了100%正確。在神經元數量上，統計分析僅用5個隱層神經元，而原始數據卻要使用20個，結合輸入維度，統計分析18維，原始數據使用930維，僅輸入層和隱層之間的前向計算就是930×20（計算輸入值）+930（計算激活值），遠大于統計分析的220（即20×10+20），增加了計算量，由此可以看出特征提取可以簡化監測模型。

眾所周知，機構各構件轉角之間關系只取決于各構件相對長度。引入長度比例系數mb(稱為凸輪偏心率)、ma和mc：

將模具溫度40、60、80 ℃分別記為1、2、3類，不同降維度方法對應的分類結果如表3所示。相比于SP方法，原始數據在訓練集、驗證集和測試集上都比它們具有更小的均方差MSE和百分誤差

%，這可能是因為SP方法僅保留了原始數據的統計特征，并沒有提取與分類相關的直接有用的數據信息。PCA方法是一種基于全局的線性特征提取方法，相比于原始數據，PCA建模具有更好的泛化能力，即在訓練集和驗證集百分誤差近似相等的情況下，在測試集上有更小的測試誤差。LE和DM擴散系數圖都是非線性降維度方法，其降維度獲得的數據建立的模型更好。

3.2 質量預測結果與討論

試驗制品成型質量分布如圖3所示，淺色線表示質量曲線，橫線表示每個工藝狀態下的平均質量，縱線區分不同的材料或模具溫度，深色曲線表示所有樣本的平均質量。由圖3可知，由于工藝差異（模具溫度）和材料狀態不同（原材料和回用料），使成型制品質量整體波動劇烈，分布具有規律性，但難以直觀地與螺桿位置、壓力曲線建立關系。以均方差為標準，從訓練集上看，原始數據的均方差最小，其次是DM、SP、LE，最后為PCA主成分分析法，表明使用原始數據訓練的模型與訓練數據匹配最好，同時這也與回歸系數的結果一致。從驗證集和測試集上看，與訓練集相反，原始數據訓練的模型在進行新的數據測試時回歸系數僅為0.8，而一般使用降維度的數據所得到的回歸系數為0.9，且均方差也小于原始數據模型，這表明由特征提取獲得的數據更加具有代表性，將SP和DM方法獲得的數據作為混合數據輸入，從表4看出獲得了更好的擬合效果。

治療后，觀察組和對照2組的臨床治療總有效率均顯著高于對照1組，差異有統計學意義（P＜0.05）；觀察組的臨床治療總有效率顯著高于對照2組，差異有統計學意義（P＜0.05）。見表2。

圖4、圖5所示是曲線原始數據與SP和DM方法降維后的混合數據在神經網絡質量預測上回歸系數的比較，其中

=

表示完全擬合，離此線越近，擬合效果越好。從圖4、圖5可知：原始數據在訓練集上回歸系數達到近0.99，但是在驗證集、測試集上僅為0.77和0.81，造成這一現象的原因有2個：①數據過擬合，通過調整正則參數或神經元數量改進；②數據并沒有代表性，即模型本身沒有發現數據內在的關系。經過試驗調整神經元數量，發現結果沒有改進，說明原因由后者造成。經過SP和DM方法降維度后，制品質量的預測值不僅在訓練集上，而且在驗證集和測試集上都表現出較高的回歸系數（>0.92），這表明采用SP和DM方法降維度后，提取了原始數據內在的高維度、非線性、強耦合的數據關系，摒棄了大量的冗余參數，提取的特征不僅使質量預測模型運行速度更快，而且提高了準確率。

4 結束語

基于采集的注塑機螺桿位置、壓力信號，分析了主成分分析法、統計分析法、拉普拉斯映射法和擴散系數圖法4種不同數據降維方法提取的特征，建立原材料、模具溫度與制品成型質量之間的神經網絡模型，進行注射成型過程的故障監測和質量預測，并設計試驗進行了驗證。試驗結果表明，通過合適的數據降維方法，可以從螺桿位置與壓力的信號中有效判斷制品的原材料、模具溫度是否正常，與未降維的數據和主成分分析法相比，拉普拉斯映射法和擴散系數圖法等非線性降維方法可以解決成型過程曲線與制品質量的強非線性問題。同樣應用在制品質量預測時，采用拉普拉斯映射法和擴散系數圖法降維后，在驗證集和測試集上都表現出高于0.92的回歸系數，這表明拉普拉斯映射法和擴散系數圖法提取了原始數據內在的高維度、非線性、強耦合的數據關系，摒棄了大量的冗余參數，使提取的特征用于質量預測模型時具有更好的精度和更高的效率，對發展基于成型過程傳感曲線的高精度故障診斷和質量預測方法、提高塑料熔體注射成型過程的自動化程度具有重要意義。

[1]劉 陽.注塑制品質量參數在線檢測、建模與優化方法研究[D].沈陽:東北大學,2010:8-9.

[2]周 俊,黃志高,周華民,等.注射模型腔壓力監控系統的設計與實現[J].模具工業,2014,40(6):10-14.

[3]楊 潔.基于PCA的間歇過程監測及故障診斷方法研究[D].沈陽:東北大學,2010:5-49.

[4]李華偉,李 陽,郭 飛,等.注射模精密成型過程一致性在線監控方法研究[J].模具工業,2020,46(5):8-13.

[5]YI X H,XUAN F Z,LEEJAY,et al.Discriminant diffusion maps analysis:A robust manifold learner for dimensionality reduction and its applications in machine condition moni?toring and fault diagnosis[J].Mechanical Systems and Sig?nal Processing,2013,34(1-2):277-297.

[6]YUN Z,TING M,ZHI G H,et al.A statistical quality moni?toring method for plastic injection molding using machine built-in sensors[J].The International Journal of Advanced Manufacturing Technology,2016,85:2483-2494.

[7]馬 莉,杜小榮.基于監督學習的核拉普拉斯特征映射的FCM算法[J].工業儀表與自動化裝置,2016(4):9-12.

[8]倪家鵬,沈 韜,朱 艷,等.基于擴散映射的太赫茲光譜識別[J].光譜學與光譜分析,2017,37(8):2360-2364.

[9]王 軍,馮孫鋮,程 勇.深度學習的輕量化神經網絡結構研究綜述[J].計算機工程,2021,47(8):1-13.

[10]GUENTHERNICK,SCHONLAUMATTHIAS.Support vec?tor machines[J].The Stata Journal,2016,16(4):917-937.