質量位移效應對部分相干源關聯函數的影響

石萌萌，宋秀丹，李淑俠

（黑龍江大學 物理科學與技術學院，黑龍江 哈爾濱 150080）

為探索核-核碰撞早期形成的極端系統，高能重離子物理學應運而生.由于無法直接用肉眼觀測重離子碰撞的具體過程，現階段只能通過末態粒子觀測量的分析來反推其碰撞細節.其中，HBT 關聯函數是探尋高密高壓下極端系統特性的有效手段.HBT 關聯函數最早出現于上世紀50 年代，為了測量天體尺度，Harbury、Brown 和Twiss 利用強度干涉儀吸收到的光子數構建出關聯函數，因此發明強度干涉學分析方法，這種方法稱為HBT 關聯函數[1].1960 年，Goldhabor[2]等首次將HBT 關聯應用于高能物理實驗中.此后，這種方法被作為一種探索粒子發射源時空結構的有效手段.

當2 個重核離子相互碰撞時，粒子被沖擊壓縮，在碰撞核交疊區域產生極端高溫高密媒介系統，媒介系統經歷膨脹冷卻后射出大量自由粒子到達探測器[3-4].尚未凍出媒介系統的粒子稱作準粒子，準粒子在飛離反應區之前一直與媒介系統相互作用，這種相互作用使準粒子質量相較于真空中自由粒子質量產生變化，這一過程叫做質量位移效應[5].質量位移效應的存在會對末態粒子的關聯函數產生影響，這將有益于分析粒子發射源內部媒介系統的動量分布和狀態方程.在以往討論相對論重離子碰撞的過程中，一般選取混沌源作為粒子發射源.但隨著碰撞能量的不斷增強，片面地將粒子發射源看作是完全混沌的已不再符合實驗事實.2013 年，ALICE 合作組在的Pb-Pb 碰撞中，發現粒子的關聯性受到了明顯抑制，與完全混沌的粒子發射源相比，這種抑制使得粒子關聯函數在低動量區存在23%±8%的相干發射分數[6-7].2015 年 Wong[8]等研究了靜態球對稱諧振子平均場中全同π介子氣體的玻色-愛因斯坦凝聚，證明在重離子碰撞中的凝聚現象會導致發射源產生一定程度的相干發射.這些實驗事實可以證明若想更精確地描述粒子發射源，還應該考慮一定的相干成分.因此，在部分相干源模型下探尋質量位移效應對兩粒子關聯函數的影響更能精確地描述粒子發射源的時空結構.本文將在部分相干源模型下討論包含質量位移效應的關聯函數公式.

1 部分相干發射源模型下的兩粒子關聯函數

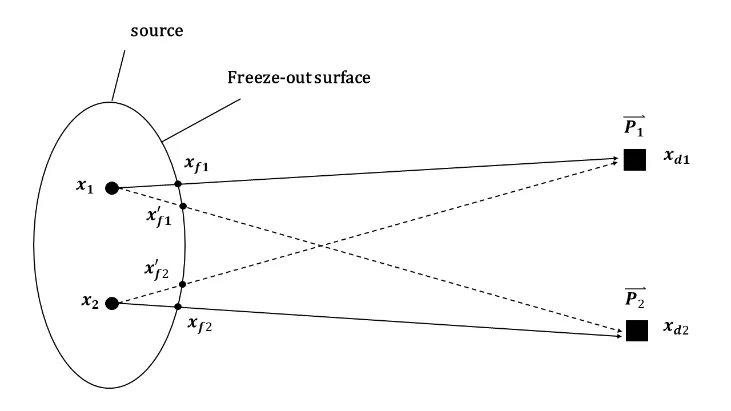
圖1 在xd1,xd2處檢測到由粒子發射源內發出兩粒子的可能路徑

對于一個部分相干發射源來說，粒子發射源分布為混沌源和相干源2部分疊加之和，因此在部分相干發射源內，動量為的2個粒子從x1,x2處發出，到x d1,xd2處被探測到，這一過程所產生的總幾率振幅為

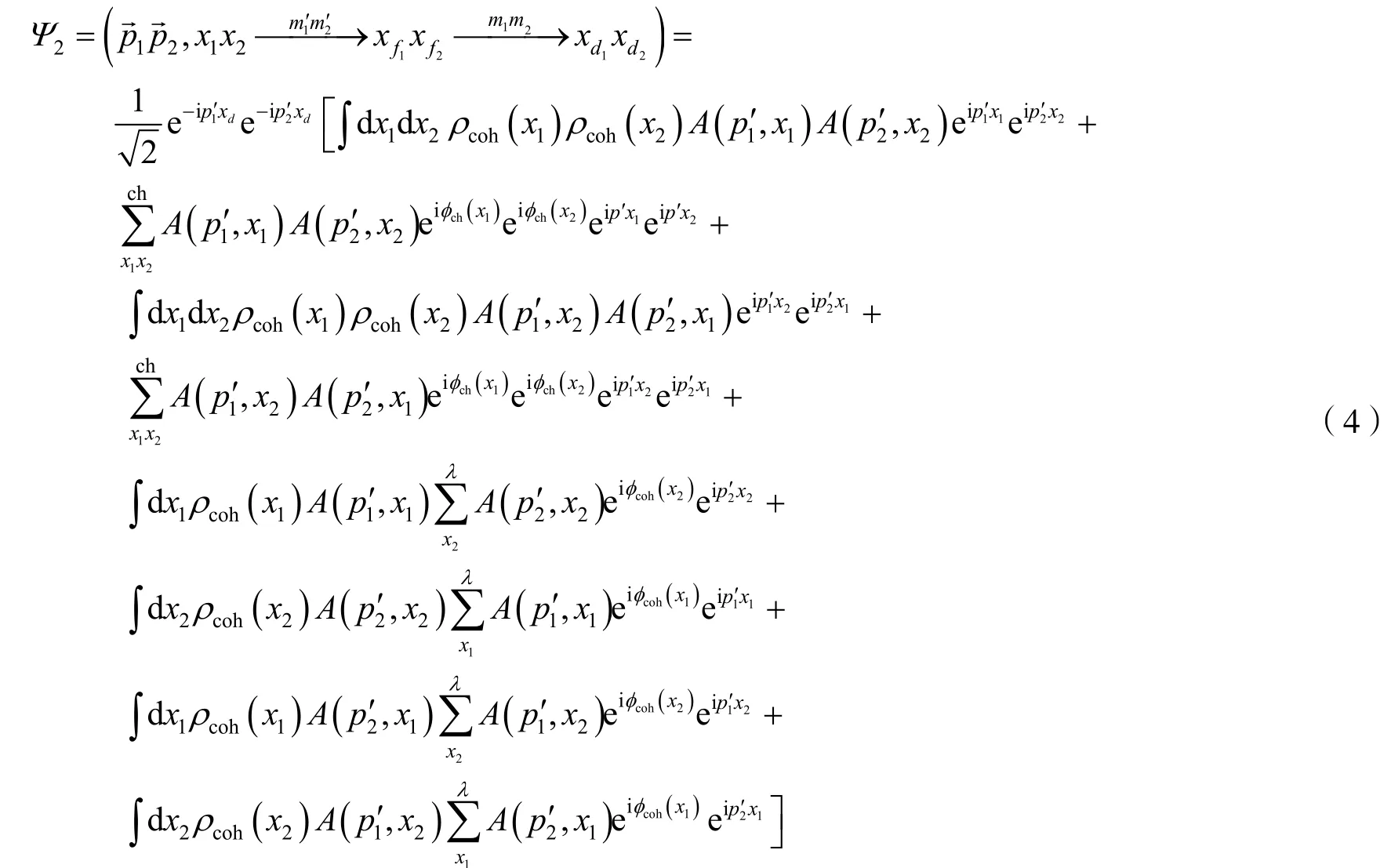
動量分布P1（→）表示發射源點x發射單個動量為p→的粒子抵達探測點xd的概率，則

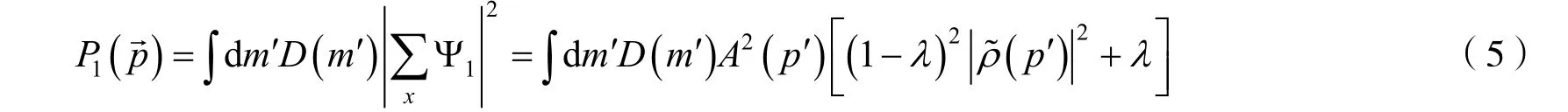
式（5）中的D（m′）是準粒子在媒介系統中的質量分布，該質量分布采用了Breit-Wigner 形式[9].Δm′=m-m′表示準粒子在媒介系統中的質量位移，Γ是介質質量寬度，根據單粒子動量分布可以得到兩粒子動量分布為P2（→ ,→）

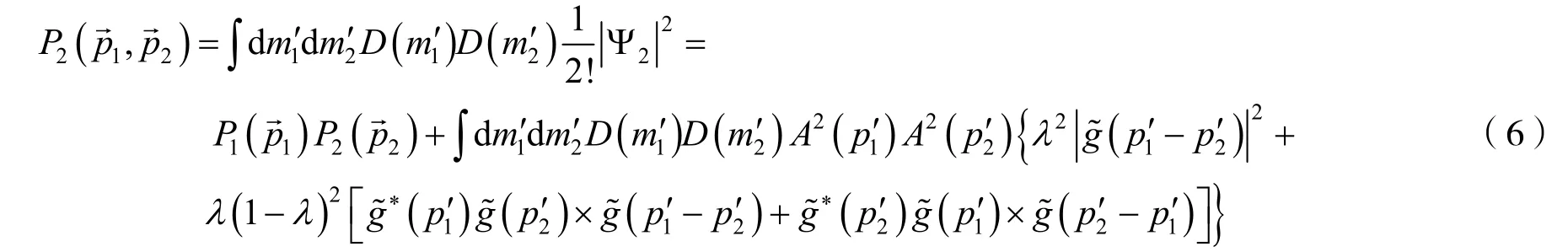
兩粒子HBT 關聯函數定義為

將式（5）（6）代入式（7）中，得到兩粒子關聯函數

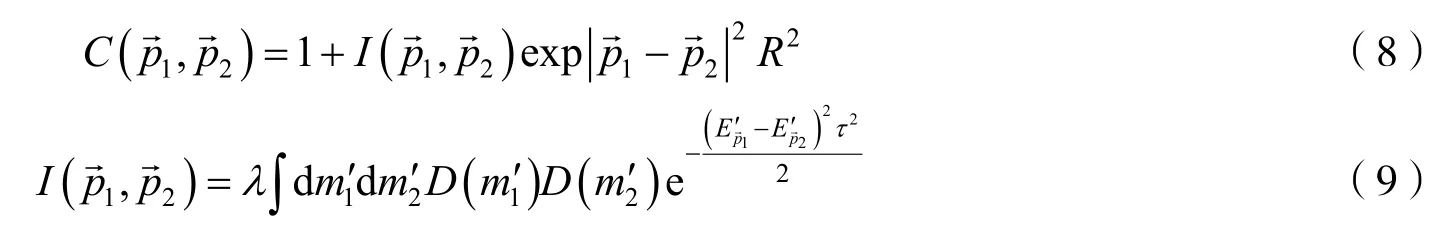
式（9）中的I（→,→）是兩粒子的關聯強度，由式（9）可得部分相干發射源的兩粒子關聯強度與粒子的質量位移和粒子發射源的混沌性參量有關.

2 質量位移效應下的部分相干粒子發射源關聯函數分析

假定粒子發射源模型為徑向膨脹的球殼模型，基于準粒子和自由粒子的質量位移效應，從兩粒子關聯函數定義出發，兩粒子關聯強度與準粒子在媒介系統中的質量分布D有關.以Φ粒子為例，計算了兩粒子關聯強度隨著粒子質量變化的關系（見圖2）.圖2a～d中粒子動量分別取0，300，500，800 MeV/c，圖中的3 條曲線分別對應質量寬度Γ為4.26，10，20 MeV/c2時，關聯強度與準粒子質量m′的關系.這里取粒子發射源的混沌性參量λ=0.8，源的壽命τ=2 fm/c，真空中自由Φ粒子的質量m=1 019.4 MeV/c2，真空中介質質量寬度Γ0=4.26 MeV/c2[10-11].

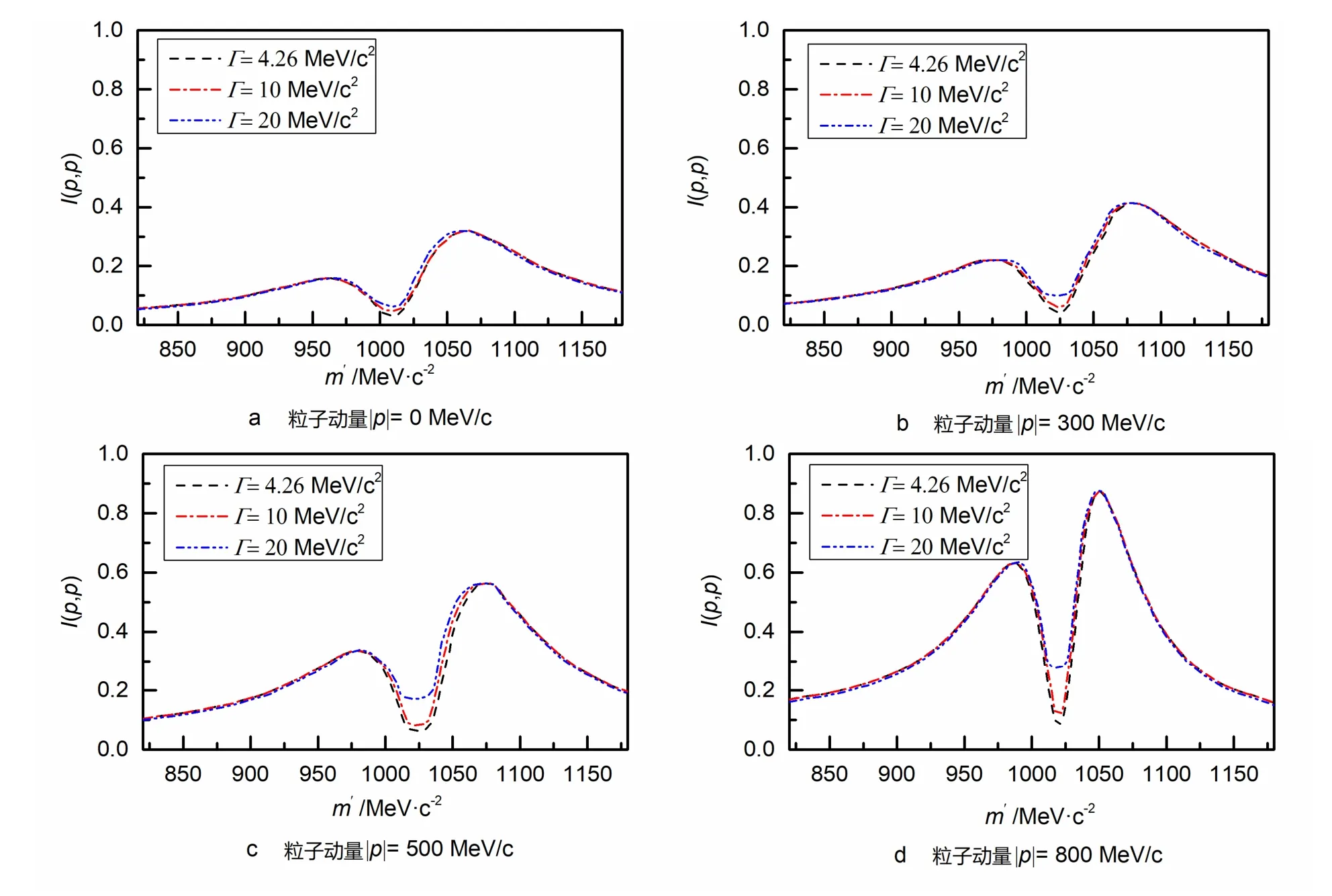
圖2 不同質量寬度Γ 下Φ 粒子質量與關聯強度的關系

從圖2 中可以看出，當介質質量寬度Γ=4.26 MeV/c2時，兩粒子關聯強度具有典型的雙峰結構，這是因為當Δm=0時，兩粒子關聯強度為1，當Δm∝±∞時，兩粒子關聯強度值也會趨于1，于是就會出現這種雙峰結構.圖中粒子發射源的混沌性參量λ取0.8，相應的兩粒子關聯強度的值小于1.當動量一定，隨著介質質量寬度Γ逐漸增強，雙峰結構的峰值緩慢增加，即粒子動量一定時，雙峰結構的峰值隨介質質量寬度Γ的變化而變化.通過比較圖2 中a～d，還發現兩粒子關聯強度隨著粒子動量的增加而增大，這是因為當粒子動量增加時，粒子能量增加，兩粒子的關聯強度也隨之增加.但是準粒子質量m′對兩粒子關聯強度的影響，存在于介質質量分布D（m′）中.當準粒子質量m′增加時，關聯強度也隨之增加，但當準粒子質量m′等于自由粒子質量m時，即粒子質量位移Δm=0時，介質質量分布D（m′）的大小僅取決于介質質量寬度Γ，對應圖像中出現的“谷底”.

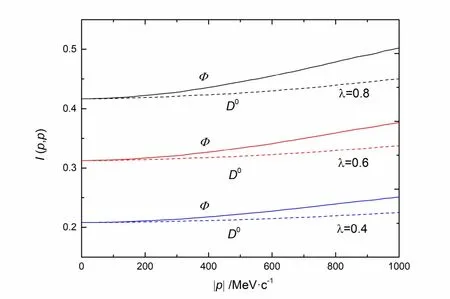
圖3 不同混沌性參量λ 下D 0粒子和Φ 粒子動量與關聯強度的關系

根據關聯強度式（9），當粒子發射源的混沌性參量達到最大值λ=1時，兩粒子關聯強度最大；當λ=0時，兩粒子關聯強度為0.從圖3中可以看出，兩粒子關聯強度都隨著混沌性參量λ的增加而增大，在大動量處，Φ粒子的關聯強度隨著混沌性參量λ的增加而顯著增大，所以Φ粒子的關聯強度對粒子發射源的混沌性參量λ還是很敏感的，這可以從式（9）中的關聯強度與混沌性參量λ的比例關系得出，但D0粒子和Φ粒子受到介質質量分布的制約，這種變化并不是線性的.

3 結論

本文采用強度干涉學的分析方法分析粒子質量位移效應對兩粒子關聯強度的影響，得到含有粒子質量位移效應的兩粒子部分相干發射源關聯函數公式.當Φ粒子的介質質量寬度取真空質量寬度ΓΦ=4.26 MeV/c2時，兩粒子關聯強具有典型的雙峰結構.當Δm=0時，關聯函數的值為1；當Δm∝±∞時，關聯函數的值也會趨近于1，于是形成了這種雙峰結構.當粒子動量一定時，隨著介質質量寬度Γ逐漸增強，雙峰結構的峰值緩慢增加，即粒子動量一定時，介質質量寬度對雙峰結構產生了影響.在媒介系統的質量分布D中，介質質量寬度大小相對于具有較寬質量分布的Φ粒子來說影響比較小.兩粒子關聯強度還與粒子發射源的混沌性參量λ有關，計算結果表明2 種粒子關聯強度都隨著混沌性參量λ的增加而增大，這表明在大動量處，Φ粒子的關聯強度隨著混沌性參量λ的增加而顯著增大，所以Φ粒子的關聯強度對粒子發射源的混沌性參量λ還是很敏感的.因此，只要確定粒子動量的大小，就能得出在不同介質質量寬度下的HBT 關聯函數曲線，將這樣的圖形稱為標準圖.將實驗數據與標準圖比對，找到與實驗數據最為相近的一條曲線，這條曲線相應的介質質量寬度和混沌性參量就可以看作是粒子發射源的介質質量寬度和混沌性參量.本文只討論HBT 關聯函數其中一方面的應用，但HBT 關聯函數的應用不止于此，利用HBT 關聯消失現象探測強子凍出信號和探測噴注現象都說明HBT 關聯函數在高能重離子碰撞中的重要應用.