凍融循環和不均勻凍脹下寒區隧道的塑性解答1)

張常光 *, 高本賢 ** 周 渭 * 李海祥 *

* (長安大學建筑工程學院,西安 710061)

? (地質災害防治與地質環境保護國家重點實驗室,成都 610059)

** (長安大學公路學院,西安 710064)

引言

季凍區隧道含水圍巖的負溫凍脹受支護約束,產生的凍脹力反作用于支護上,對隧道安全造成不利影響[1-2].作為寒區隧道工程設計的重要環節,凍脹力解析計算已得到深入研究.Lai 等[3]利用黏彈性模型建立寒區隧道凍脹力的黏彈性解,Feng 等[4]假定圍巖為各向同性均勻凍脹得到寒區隧道凍脹力的Mohr-Coulomb (MC)準則解答.實際上,寒區隧道圍巖凍脹在3 個方向上是存在差異的,冷空氣使得寒區隧道在徑向上呈現明顯的溫度梯度,繼而圍巖凍脹表現為以徑向凍脹為主,切向和縱向的凍脹次之且程度相同[5-6].Lü等[7]考慮圍巖凍脹的不均勻性,基于MC 準則求得寒區隧道的凍脹力塑性解.

季凍區隧道圍巖凍結圈形成后會經歷長期凍融循環,每次凍融循環都將導致巖體一定程度的損傷、可能形成新裂隙,融化的水會充滿裂隙再次凍結,如此循環使得圍巖孔隙率升高、承載性能劣化,凍脹力也隨之增大,最終造成支護開裂或因荷載明顯增加而失效[8-9].前面所提到的寒區隧道凍脹力解答[3-4,7]均針對單次凍結,未考慮凍融循環對圍巖承載性能的劣化效應.大量的巖石凍融試驗表明[10-14]:凍融次數的增加會引發巖石的孔隙率增大,彈性模量、黏聚力和內摩擦角呈明顯下降趨勢,進而使巖石承載能力降低.劉泉聲等[15]認為圍巖凍融損傷伴隨原有裂隙的發展、貫通以及新裂隙的出現.張慧梅等[16]利用CT 掃描研究了凍融巖石的細觀損傷演化規律,指出巖石有效承載區隨凍融次數的增加而減小.Liu 等[17]假設每次凍融造成巖石細觀損傷的程度相同,基于彈性解答提出考慮凍融循環損傷的寒區隧道凍脹力計算模型;劉紅巖等[18]引入未凍結圍巖約束作用和凍融循環下微裂紋擴展規律及巖石凍脹率變化,改進了文獻[17]中的寒區隧道凍脹力彈性解.

可見,目前鮮有凍融循環下寒區隧道凍脹力的解析計算,文獻[17-18]已有研究只進行了彈性分析且未考慮圍巖凍脹的不均勻性.當圍巖承載能力低、凍脹顯著或受高地應力作用時,季凍區隧道圍巖易進入屈服狀態,凍脹力的彈性解答不再適用.因此,本文合理考慮寒區隧道圍巖不均勻凍脹和凍融循環劣化效應,以MC 準則為屈服判據推導寒區隧道凍脹力、應力與位移的塑性解答,同時給出相應的彈性解答,繼而對所得結果進行可比性分析、給出適用性判定方法,并與文獻塑性解答[7]進行對比驗證,最后探討凍融循環、不均勻凍脹和體積凍脹率對季凍區隧道性能的影響規律.

1 基本假定

為得到便于工程應用的季凍區隧道塑性解答,特做以下基本假定:

(1) 采用凍融圈整體凍脹模型[1],忽略圍巖的實際凍脹過程,也不計隧道開挖和支護的時間,將鋪設保溫層、設置排水溝等防凍措施改善寒區隧道洞壁位移、凍脹力等現場數據變化的實際成效,通過綜合對比本文理論計算結果納入年凍融次數Na的調整.

(2) 圓形隧道受等值地應力作用(實際隧道斷面非圓形按面積相等的當量半徑轉化為圓形[19]),支護與圍巖的受力分析簡化為平面應變繞軸對稱問題,并以壓應力為正.

(3) 隧道圍巖屬于以徑向凍脹為主、切向和縱向凍脹次之且程度相同的不均勻凍脹,忽略凍脹對圍巖物理力學性能的各向異性影響[5-7];凍結圍巖為符合MC 準則的理想彈塑性材料,未凍結圍巖不發生屈服;支護為均質彈性的等厚混凝土圓環襯砌,不考慮支護區混凝土的凍融損傷.

(4) 開放條件(在隧道施工和運行中均有地下水補給,使得凍結過程中的水分遷移顯著,圍巖也更易發生凍脹[20])下凍結圍巖經N次凍融后的體積凍脹率為[11,21]

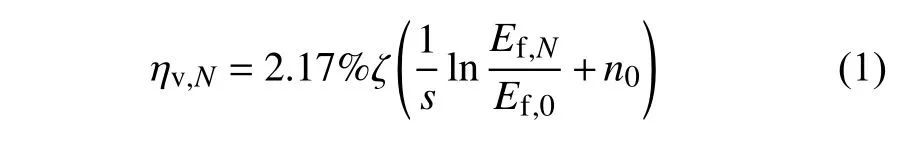
式中,下標N代表凍融次數與狀態,0 代表凍結-未融化狀態;ζ為水熱遷移系數,取值與圍巖凍脹敏感性有關[21],凍脹敏感圍巖取1.58,凍脹非敏感圍巖取1.0;s為擬合參數,可依據巖石凍融循環試驗擬合獲得;E為彈性模量,下標f 代表凍結圍巖(后文亦有上標f,意同);n0為凍結-未融化狀態下圍巖的孔隙率.需注意的是,本文所有上/下標均指代唯一、全篇通用.

(5) 凍融循環造成凍結圍巖的長微裂紋擴展但形狀不變,文獻[18]基于Griffith 斷裂理論及細觀損傷力學提出凍融循環下以長微裂紋條數變化描述凍結圍巖彈性模量的劣化規律為

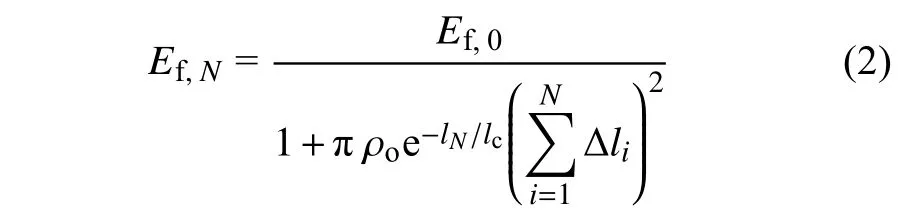
式中,ρo為單位面積微裂紋條數即微裂紋密度,lN為經N次凍融后的微裂紋擴展半長,lc為微裂紋分布參數;為第i次凍融循環所導致的微裂紋擴展半長;ω為微裂紋長軸與短軸的長度變化量之比;以上參數均可由凍融循環下巖石CT 技術獲得;m為溫度降低引起的圍巖彈性模量放大系數,通常取1～ 2[18];KI為冰的體積模量.

2 寒區隧道彈塑性解答

寒區隧道凍脹力、應力與位移的彈塑性解答以凍結圍巖是否進入屈服狀態分為塑性解答(凍結圍巖部分屈服)、彈性解答(凍結圍巖未屈服).

2.1 塑性解答

由巖體凍脹性分級[19]和基本假定知,式(1)～式(2)對圍巖均勻凍脹和不均勻凍脹均適用.假設凍結圍巖已部分進入屈服狀態,此時寒區隧道的塑性力學模型如圖1 所示,其中季凍區圍巖凍結范圍可根據隧道多年實測溫度場與當地經驗或半解析法確定[22].在圖1 中,ro為支護的內半徑,r1為支護的外半徑,rp為凍結圍巖的塑性區半徑,r2為凍結圍巖的彈性區外半徑;po為初始地應力,P1為凍結圍巖與支護交界處的徑向正應力,P2為凍結圍巖與未凍結圍巖交界處的徑向正應力,Pp為凍結圍巖彈-塑性交界處的徑向正應力.

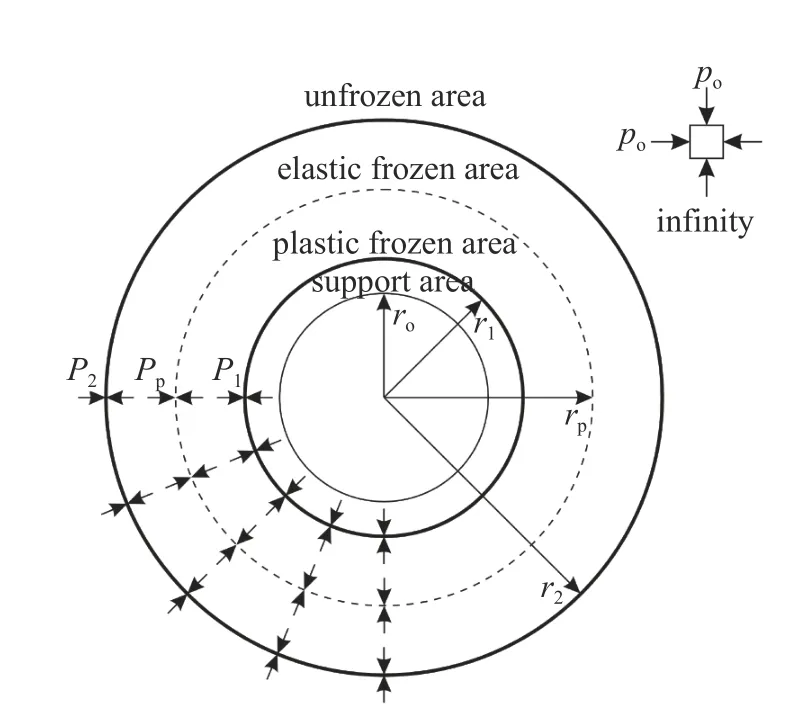
圖1 寒區隧道塑性力學模型Fig.1 Plastic mechanical model of a cold region tunnel

在構建寒區隧道塑性解答時,未凍結圍巖區和支護區均符合彈性力學的厚壁圓筒理論,凍結圍巖彈性區以平面應變增量彈性本構方程為基礎,凍結圍巖塑性區需結合MC 準則,同時各區交界處要滿足應力連續條件和位移連續條件(r=r1處支護區與凍結圍巖塑性區交界、r=rp處凍結圍巖彈-塑性交界、r=r2處凍結圍巖彈性區與未凍結圍巖區交界).

2.1.1 未凍結圍巖區和支護區

根據彈性力學厚壁圓筒理論,得未凍結圍巖區與支護區的應力分別為[23]

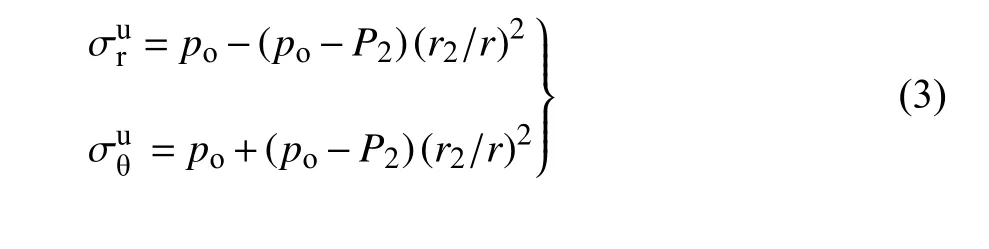
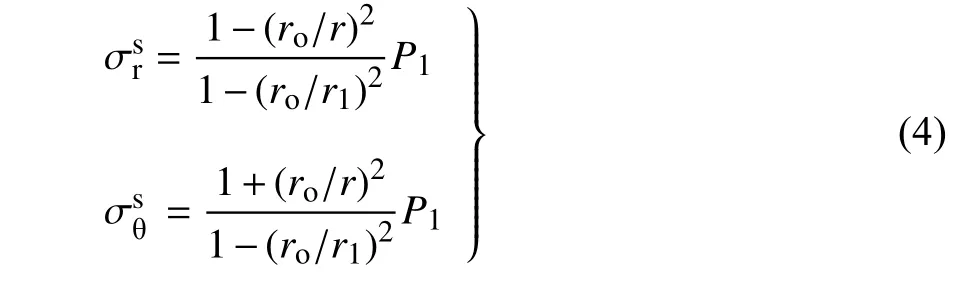
式中,σr為徑向正應力,σθ為切向正應力;下標r 代表徑向,θ 代表切向;上標s 代表支護、u 代表未凍結圍巖(后文亦有下標s 和u,意同);r為極坐標下支護或圍巖中某點到隧道中心的距離.相應的徑向位移分別為

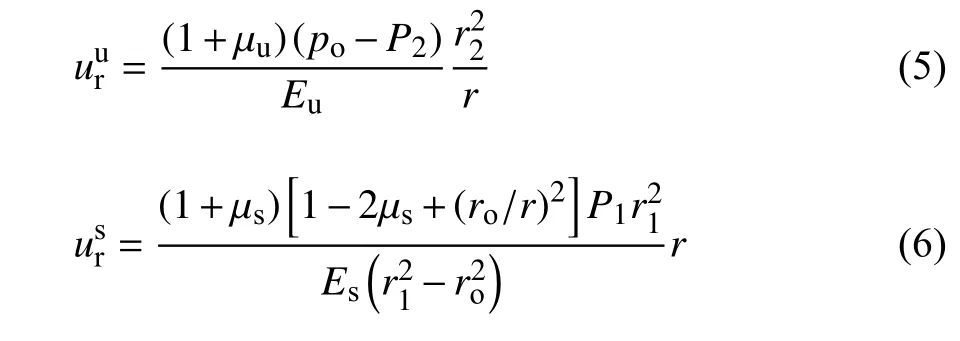
式中,u為位移,以指向隧道中心為正;μ為泊松比.

2.1.2 凍結圍巖彈性區

凍結圍巖線應變包括應力變化部分和凍結膨脹部分,其表達式即平面應變增量本構方程為[5]

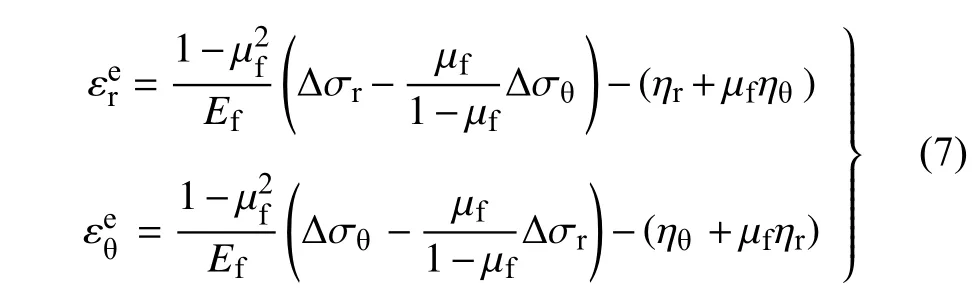
式中,εr為徑向線應變,εθ為切向線應變,上標e 代表彈性狀態;Δσr,Δσθ為徑向與切向的正應力增量,且有Δσr=σr-po,Δσθ=σθ-po;ηr,ηθ,ηz為寒區隧道徑向、切向和縱向的線凍脹率,且切向與縱向的凍脹程度相同即ηθ=ηz,體積凍脹率ηv=ηr+ηθ+ηz=ηr+2ηθ;不均勻凍脹系數k=ηr/ηθ,一般忽略凍脹過程中微/宏觀裂隙擴展演化而假定為1～ 3 的常數[1],并有ηr=kηv/(k+2),ηθ=ηz=ηv/(k+2),凍結區水分的不均勻分布加劇了寒區隧道徑向主凍脹,使得不均勻凍脹系數k和體積凍脹率ηv均有所增加.

凍結圍巖的平衡方程為

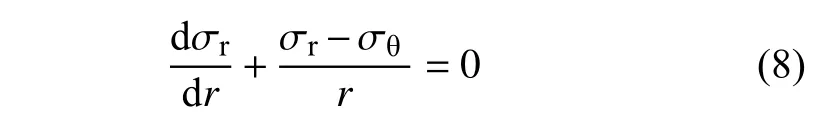
2.1.3 凍結圍巖塑性區

以MC 準則作為凍融循環后圍巖的屈服準則[24],在凍結圍巖塑性區內σθ為大主應力σ1,σr為小主應力σ3,則

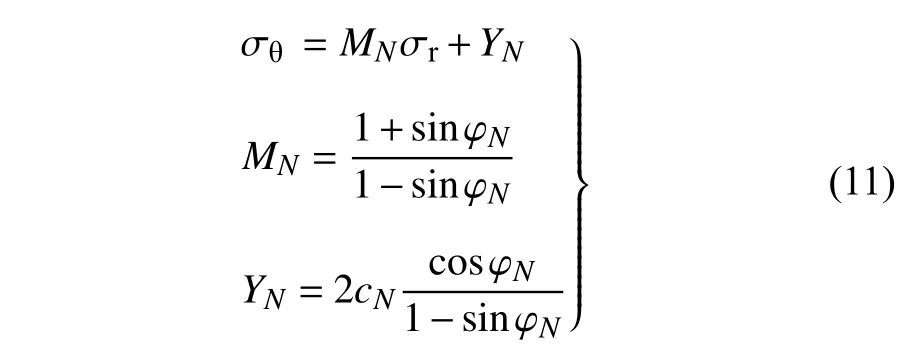
式中,MN,YN為方程參數;c,φ為凍結圍巖的黏聚力和內摩擦角,且有[13]cN=ca+cbeαN,φN=φa+φbeξN,其中ca,cb,α和φa,φb,ξ均為擬合系數,可通過巖石凍融循環直剪試驗確定.

聯立式(8),式(11)和應力邊界條件σr|r=r1=P1,積分得凍結圍巖塑性區的應力為

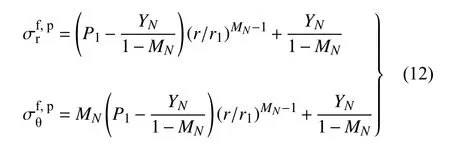
式中,上標p 代表塑性狀態.

采用線性非相關流動法則,結合幾何方程εr=dur/dr,εθ=ur/r與式(7)和式(12),以彈-塑性交界處為位移邊界條件,得凍結圍巖塑性區的徑向位移為

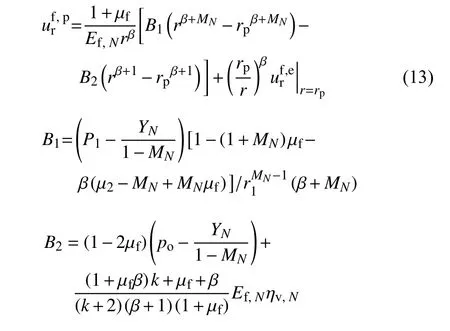
式中,β為剪脹特征參數.

2.1.4 凍脹力

在彈-塑性交界處凍結圍巖彈性區的應力也滿足MC 準則即式(11),則

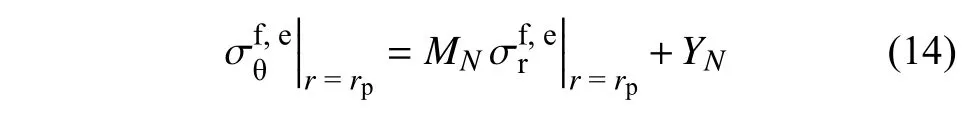
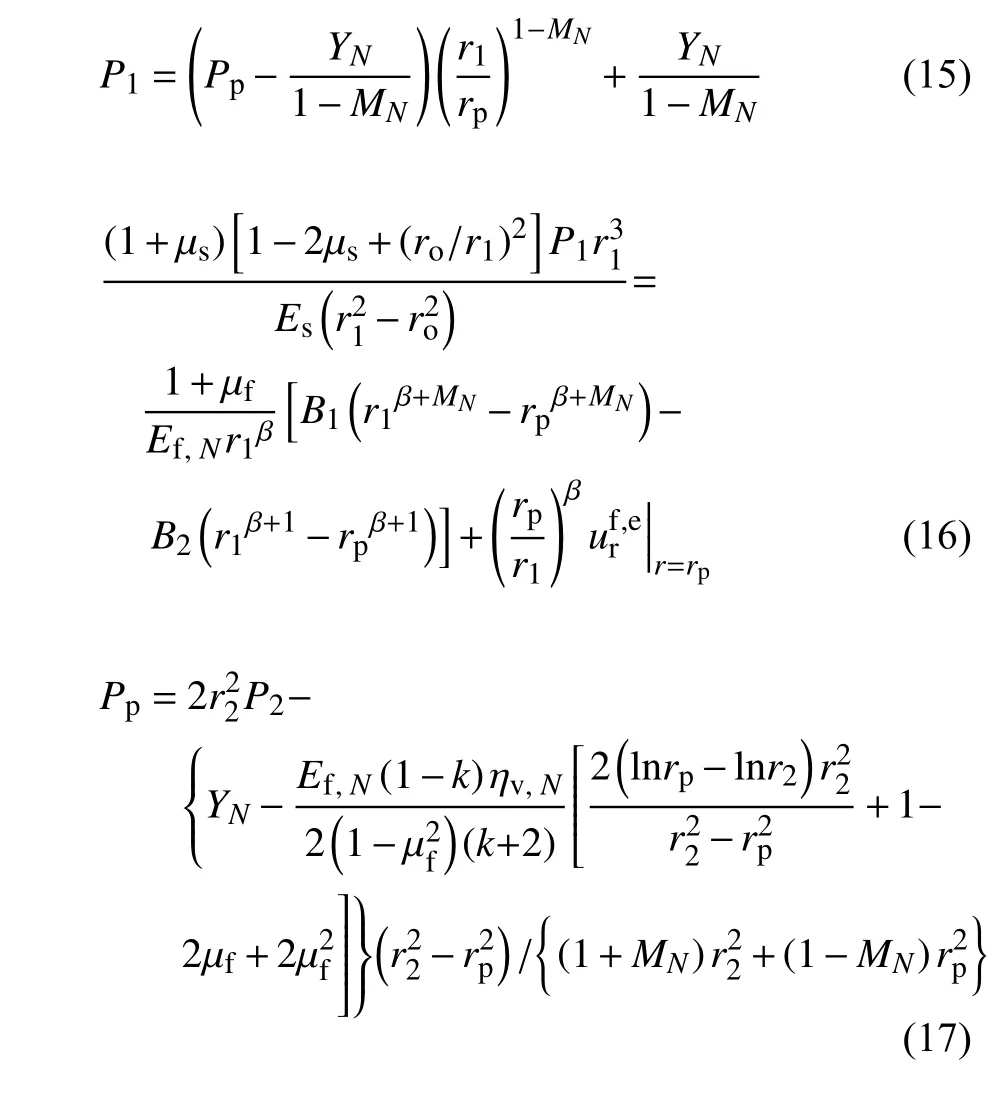
將式(15)代入式(6)并令r=r1,得寒區隧道的洞壁位移ua為

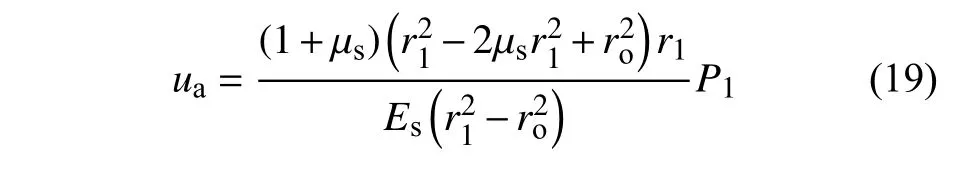
由式(15)求得的P1為總支護壓力,包括凍結前圍巖作用在支護上的初始徑向正應力(按支護與未凍結圍巖雙層厚壁圓筒計算)[25],故寒區隧道圍巖作用在支護上的凍脹力ΔP1為

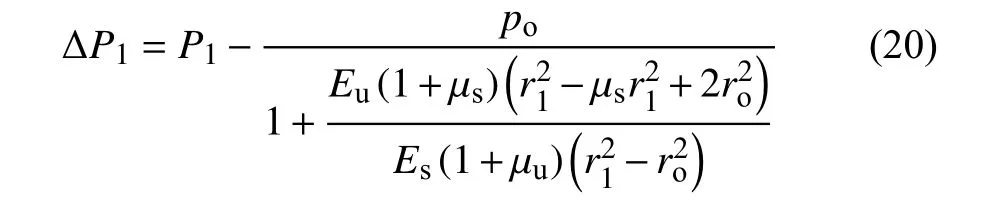
2.2 彈性解答及彈-塑性狀態判定

寒區隧道凍結圍巖未進入屈服狀態時,應采用其彈性力學模型,如圖2 所示.相比寒區隧道塑性力學模型及其解答,此時凍結圍巖完全彈性而不存在彈塑性分區,只剩r=r1處支護區與凍結圍巖區交界、r=r2處凍結圍巖區與未凍結圍巖區交界,凍結圍巖內緣r=r1處應力不滿足MC 準則,其他求解思路同2.1 節.

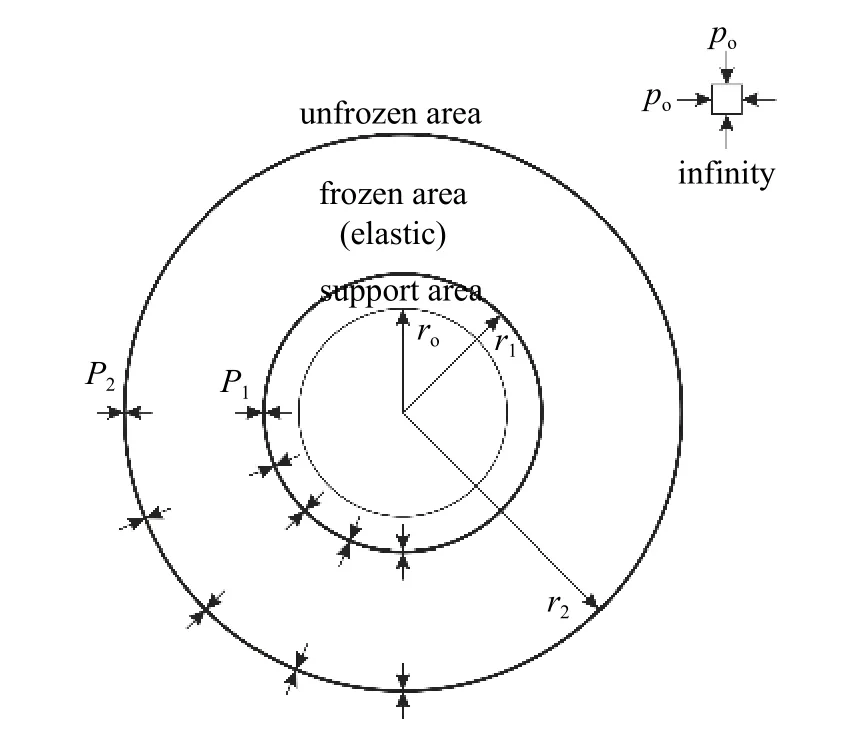
圖2 寒區隧道彈性力學模型Fig.2 Elastic mechanical model of a cold region tunnel

未凍結圍巖區及支護區的應力和位移仍為式(3)～式(6),而凍結圍巖區應力與位移表達式中的A1,A2變為

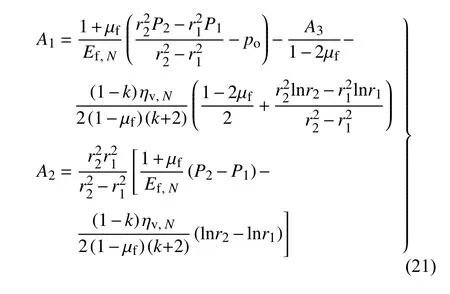
將式(21)分別代入式(9)和式(10),得彈性狀態下寒區隧道凍結圍巖區應力與位移的具體表達式.

式中

將式(22a)分別代入式(19)和式(20),得寒區隧道彈性狀態下的洞壁位移ua與凍脹力ΔP1.

對于寒區隧道的彈-塑性狀態判定,可將式(22)代入式(21),再將結果代入式(9)并令r=r1,得彈性狀態下凍結圍巖內緣處的應力,繼而將其代入MC準則即式(11)進行判定:當σθf,e＜MNσrf,e+YN時凍結圍巖保持彈性狀態、無塑性區,否則進入屈服狀態.也可通過凍結圍巖塑性區半徑rp與支護外半徑r1的相對大小進行判斷:當rp＜r1時凍結圍巖保持彈性狀態、無塑性區,否則進入屈服狀態.

3 可比性及驗證

本文綜合考慮寒區隧道圍巖不均勻凍脹屬性和凍融循環對凍結圍巖性能的劣化效應,采用MC 準則建立了寒區隧道凍脹力、應力與位移的塑性解答:式(20)為凍脹力解答,式(3)、式(4)、式(9)和式(12) 為應力解答,式(5)、式(6)、式(10) 和式(13)為位移解答,式(16)為塑性區半徑的隱式計算方程,還給出了凍結圍巖彈-塑性狀態的判定方法,同時得到了寒區隧道的彈性解答,可為季凍區隧道設計提供一定的理論指導.所建立的寒區隧道MC 準則解答在一定條件下可退化為其他理論解.例如,系數k=1 時為各向均勻凍脹解答[4,17-18],次數N=0 對應不考慮凍融循環損傷的解答[3-5,7].因此,本文結果具有很好的可比性,可根據工程實際情況進行合理選擇,具有重要的理論意義和應用價值.

Lü等[7]推導了不均勻凍脹寒區隧道的MC 準則解答,但未考慮凍融循環對圍巖性能的劣化效應.當凍融次數N=0 時,本文結果退化為文獻[7]解答.取表1 寒區隧道的塑性狀態參數進行計算和對比,如圖3 所示.可見,本文塑性解(N=0)與文獻[7]的凍脹力、塑性區半徑完全吻合,驗證了本文退化結果的正確性.

表1 寒區隧道的塑性狀態參數[7]Table 1 Plastic state parameters of a cold region tunnel[7]

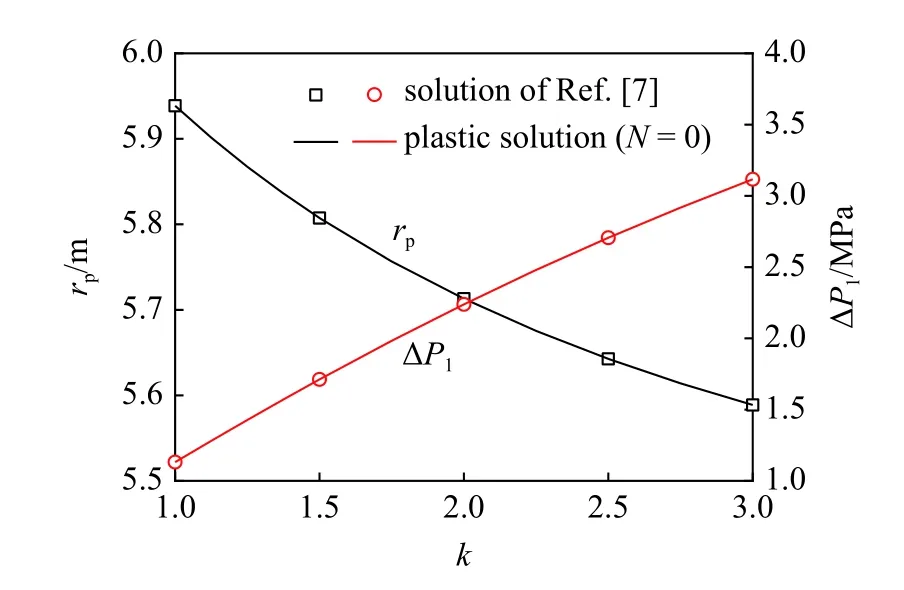
圖3 本文塑性解(N=0)與文獻[7]解答的對比Fig.3 Comparisons between plastic results from this study with N=0 and Ref]7]

4 參數分析

對于未鋪設保溫層或防凍措施不佳的季凍區隧道,本文綜合考慮短周期和季節性兩類凍融[26],建議年凍融次數Na取2～ 3;對于鋪設保溫層、設置排水溝且實測溫度表明防凍有效、圍巖未經歷凍融的寒區隧道,年凍融次數Na可謹慎地取0～ 1,并根據溫度實測動態調整年凍融次數Na.探究凍融循環、不均勻凍脹以及體積凍脹率對寒區隧道應力分布、塑性區半徑、洞壁位移和凍脹力等的影響規律具有工程實際意義.長期凍融循環對季凍區隧道安全造成不利影響,借助凍融次數N可量化凍融循環劣化效應;不均勻凍脹可通過不均勻凍脹系數k來體現;體積凍脹率ηv反映圍巖的凍脹程度,受微裂紋密度ρo,微裂紋分布參數lc,水熱遷移系數ζ和擬合參數s等的直接或間接影響.采用表2 所示寒區隧道參數進行本節的計算和分析.

表2 寒區隧道參數[13,18]Table 2 Parameters of a cold region tunnel[13,18]

4.1 凍融循環

當系數k=1.5 時,由節2.2 知凍結圍巖內緣在凍融次數N=29～ 30 之間進入屈服狀態,即N≤29 時凍結圍巖處于彈性狀態、N≥30 時凍結圍巖處于塑性狀態.彈性狀態下N=0,15,29 時寒區隧道的應力分布如圖4(a) 所示,圖中區域劃分及應力標注以N=15 時為例;塑性狀態下N=45,60,75 時寒區隧道的應力分布如圖4(b)所示,圖中區域劃分及應力標注以N=60 時為例;凍融次數N對寒區隧道凍脹力和塑性區半徑的影響如圖4(c)所示,對隧道洞壁位移的影響如圖4(d)所示.

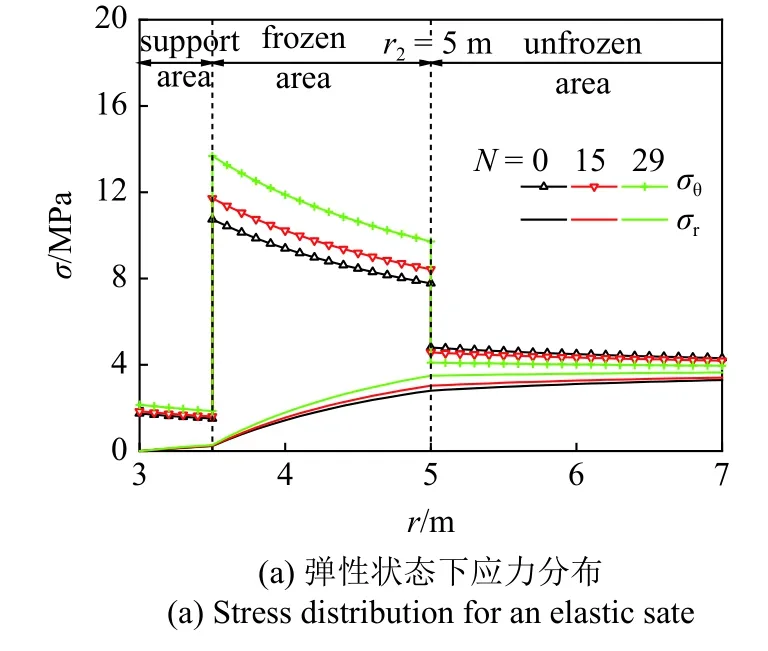
圖4 凍融循環的影響Fig.4 Influences of freeze-thaw cycles

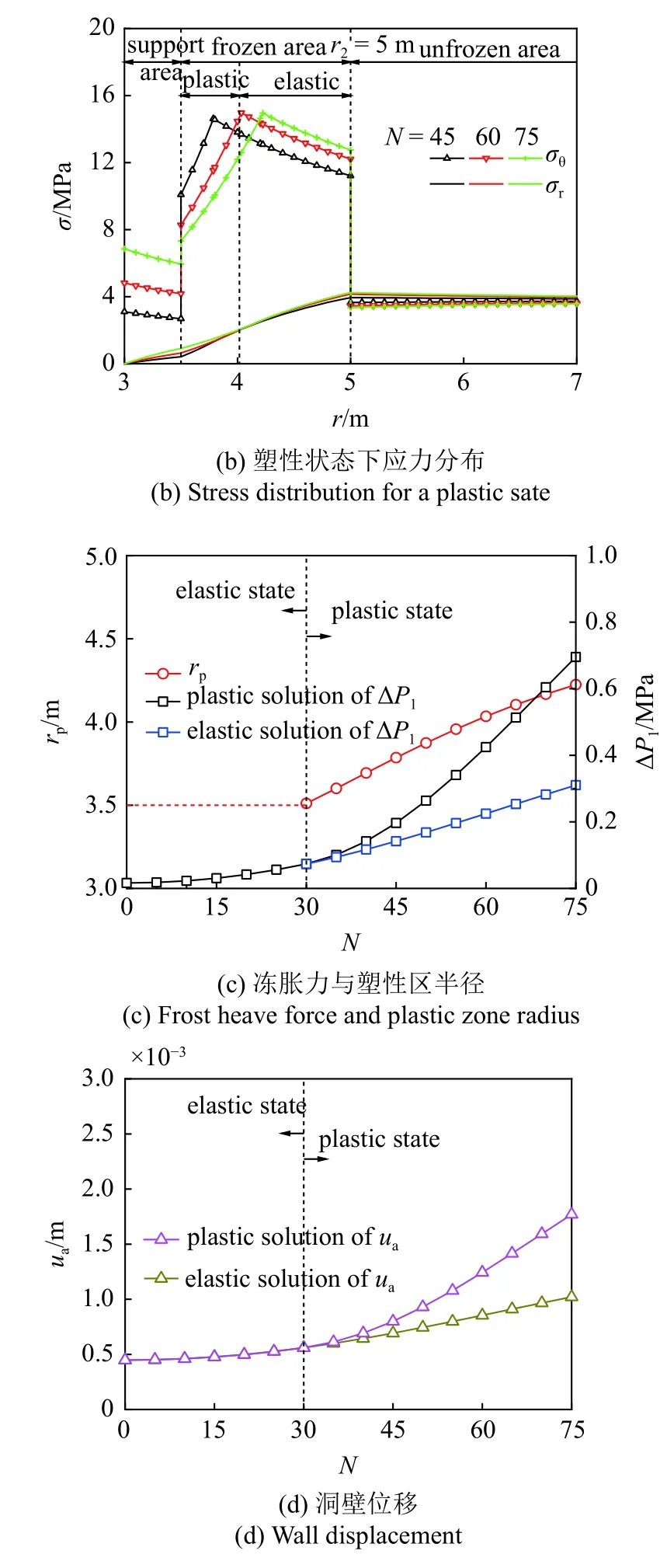
圖4 凍融循環的影響(續)Fig.4 Influences of freeze-thaw cycles (continued)

由圖4(a),圖4(b)可知,隨著凍融次數N的增加,徑向正應力σr逐漸增大,切向正應力σθ在支護區和彈性狀態下凍結圍巖區呈遞增趨勢,而在未凍結圍巖區和塑性狀態下凍結圍巖區逐漸減小,彈-塑性交界面處切向正應力σθ的峰值有所增大;凍結圍巖內外緣處的切向正應力σθ均出現跳躍,這是由于內緣處凍結圍巖與混凝土支護、外緣處凍結圍巖與未凍結圍巖的材料參數不同.

由圖4(c)和圖4(d)可知,塑性區半徑、凍脹力及洞壁位移均隨凍融次數N的增加而增大,且系數k=1,3 時的變化趨勢一致.當N從30 增加至75 時,塑性區半徑由3.51 m 擴大至4.43 m 而增大了20.3%,凍脹力塑性解增大了8.44 倍,洞壁位移塑性解增大了2.16 倍.這些都說明凍融循環對寒區隧道安全具有非常不利的影響,季凍區隧道工程設計時需重視并量化凍融循環導致的凍結圍巖性能劣化效應,采取良好的防排水和防凍措施.另外,N越大彈性解與塑性解的差異就越大,故面對復雜多變的寒區地質條件宜采用本文塑性解答.

4.2 不均勻凍脹

結合節2.2 中凍結圍巖彈-塑性狀態的判別方法,當凍融次數N=60 時,無論不均勻凍脹系數k在[1,3]區間內取何值,凍結圍巖都會進入屈服狀態.凍脹力與塑性區半徑隨系數k的變化,如圖5 所示.

由圖5 可知,當k從1 增加到3 時,凍脹力增大了42.8%,塑性區半徑僅減小了0.01 m,這表明圍巖不均勻凍脹僅在很少程度上限制了隧道塑性區的發展,但凍脹力隨圍巖不均勻凍脹程度的增加而明顯增大,凍融次數N=70,80 時凍脹力和塑性區半徑的變化規律相同,應考慮圍巖不均勻凍脹對寒區隧道凍脹力的顯著影響,采取一定保溫防凍措施既能減輕圍巖凍融循環劣化又會降低隧道徑向主凍脹危害.

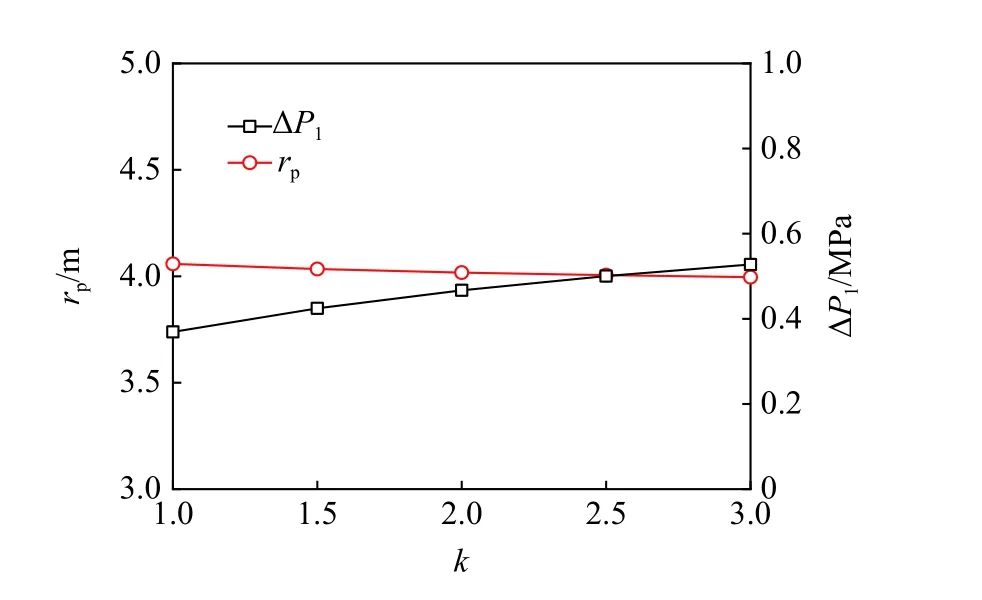
圖5 不均勻凍脹的影響Fig.5 Influences of the non-uniform frost heave

4.3 體積凍脹率

微裂紋密度ρo、微裂紋分布參數lc、水熱遷移系數ζ以及擬合參數s通過體積凍脹率ηv對寒區隧道凍脹力、塑性區半徑的影響,如圖6 所示,其中N=60,k=1.5.

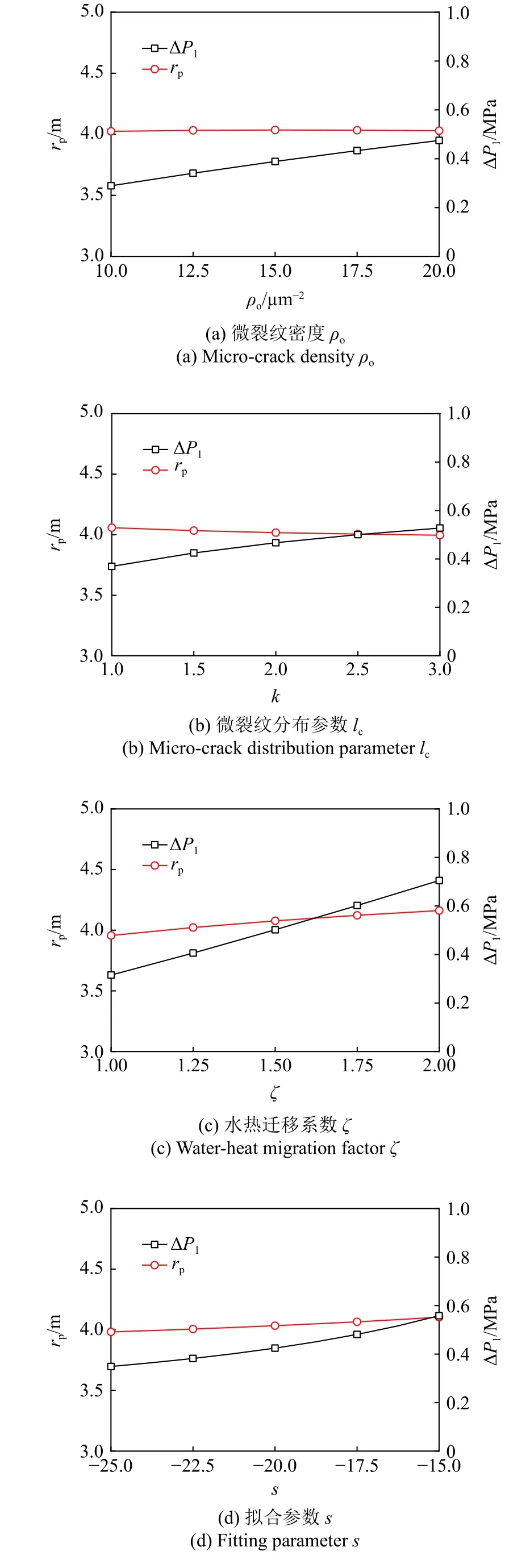
圖6 體積凍脹率的影響Fig.6 Influences of the volumetric frost heave ratio

由圖6 可知,4 種體積凍脹率參數對凍脹力和塑性區半徑的影響趨勢相似,且塑性區半徑的變化均不明顯.當微裂紋密度ρo由10 μm-2增加到20 μm-2、微裂紋分布參數lc由0.5 μm 增加到0.6 μm、水熱遷移系數ζ由1 增至2、擬合參數s由-25 增加到-15 時,凍脹力分別增大了64.2%,33.6%,123.6%和60.1%,可見水熱遷移系數ζ的影響最明顯,即凍脹敏感性圍巖的凍害程度最大.因此,應結合巖石凍融循環實測數據和CT 技術對體積凍脹率相關參數進行針對性測定或擬合取值,以保證季凍區隧道凍脹力計算的有效性.

5 結論

(1) 所建立的寒區隧道塑性解答合理考慮了凍融循環引起的圍巖性能劣化與圍巖凍脹的不均勻性,具有很好的可比性且得到文獻[7]塑性解答的退化驗證,可為季凍區隧道工程設計提供理論參考.

(2) 凍脹力和洞壁位移的塑性解答相比彈性解答大的多,受凍融次數的影響也更顯著.季凍區隧道圍巖由于長期凍融循環的性能劣化效應易進入屈服,采用塑性解答更能反映隧道的實際服役性態.

(3) 凍脹力、塑性區半徑和洞壁位移均隨凍融次數增加而增大,其中凍脹力增大達8 倍之多;凍脹力與圍巖不均勻凍脹程度成正比,4 種體積凍脹率參數特別是水熱遷移系數對凍脹力的影響顯著.

需指出的是,本文寒區隧道塑性解答是在諸多假定下構建和驗證的,可在以下4 個方面進一步完善:①依據塑性區與凍結圍巖區的相對大小,提出塑性區超過凍結圍巖區而擴大至未凍結圍巖區[27]或凍結圍巖區、未凍結圍巖區同時部分屈服的力學模型,并考慮支護區混凝土的凍融損傷;② 確定不均勻凍脹系數與微觀裂隙走向、形狀、長度以及凍結區水分不均勻分布的幾何定量表達式[28-29],且反映宏觀裂隙開裂拓展引發的圍巖劣化、導水通道貫通等,對體積凍脹率亦然;③表征凍結溫度對凍結區范圍、凍結圍巖強度、體積凍脹率的綜合作用[30],以分析凍結溫度對寒區隧道應力分布、塑性區半徑、洞壁位移和凍脹力的影響特性;④ 囿于應用本文寒區隧道塑性解答要由巖石凍融循環試驗和CT 技術測定或擬合體積凍脹率細觀參數以及圍巖強度劣化規律,暫未查詢到可供對比的寒區隧道模型試驗、現場實測或數值模擬數據,結合具體寒區巖體工程有針對性地開展隧道現場監測與模型試驗、巖石凍融循環試驗,持續優化參數數目及確定方法,對所建立的寒區隧道塑性解答進行充分性驗證及工程實踐推廣.