面向非正交多址接入無人機系統的能效優化算法

陳德全

(重慶幼兒師范高等專科學校兒童智能科學與技術系，重慶 404047)

0 引言

地震、洪水等自然災害對地面通信系統有毀滅性影響。一旦發生災害，災區居民的通信需求迅速增加，使通信負荷急劇增長。同時，災害可能破壞了原有通信設備，降低了對災區居民的服務質量。然而，保持通信暢通是開展災區救援工作的前提條件[1]。由于維修或者重建通信系統耗時且不易操作，利用無人機組建應急通信系統是行之有效的方法。與傳統的固定基站相比，利用無人機作為空中基站可極大地提高災區居民(地面用戶)的通信質量[2]。

此外，非正交多址接入(non-orthogonal multiple access, NOMA)技術是5G無線通信的重要技術，其允許多個用戶以不同功率將多個信息流在同頻域信道上傳輸[3]，即NOMA技術能夠在相同的資源上為多個用戶提供無線通信業務。NOMA的基本思想為：發送端采用正交傳輸數據，主動引入干擾信息；在接收端通過串行干擾刪除(successive interference cancellation, SIC)[4]技術進行解調，進而提高頻譜利用率。

研究人員將NOMA應用于無人機基站通信網絡[5-11]，提高通信服務質量，文獻[5]基于功率域的NOMA網絡模型，提出了基于用戶配對的能效無人機部署策略；文獻[6]分析了功率分配和最大化下行鏈路速率問題。

然而，這些研究工作并沒有在滿足用戶端的信號質量、用戶向無人機傳輸數據時延的約束條件下，討論無人機能效問題，為此，文中針對單架無人機覆蓋多個用戶的場景，通過優化無人機的高度，最大化無人機能效，提出用戶服務質量約束下無人機能效優化算法(energy-efficient optimization algorithm under quality of service constraints, EEOA)。采用NOMA技術，用戶向無人機傳輸信號，接收端(無人機)采用SIC技術分離各用戶信號。

主要研究內容包括：

1) 構建最大化無人機能效的目標函數，并考慮兩個約束條件：無人機高度和用戶通信服務質量。服務質量包含兩項指標。第一項指標是用戶端信噪比不小于預設閾值，該指標保證無人機端能夠成功解碼用戶信號；第二項指標是無人機為用戶提供充足的服務時間，該指標保證每個用戶有充足的時間向無人機傳輸數據。

2) 通過對目標函數進行處理，將兩個約束條件轉換成關于無人機高度的函數。

3) 求解目標函數，獲取無人機能效最大化的無人機高度值。

1 系統模型

1.1 網絡模型

考慮如圖1所示的網絡模型，將網絡中一個無人機作為空中基站和無線接入點。UAV收集在其覆蓋范圍內用戶的數據。這些用戶均勻分布在UAV在地面的覆蓋區域內。此外，無人機在地面上配備控制器，該控制器控制UAV的位置。

圖1 網絡模型

假定無人機配備半功率波束的有向天線，依據文獻[12-13]可知，天線在方向(φ,ω)上的增益為：

(1)

式中g0≈2.2846[12]。

所有用戶配備全向天線，在相同時間和頻率資源上向無人機發送自己的數據。但是所有用戶發送數據的功率不同，因此它們形成上行鏈路的功率域-NOMA(power-NOMA, P-NOMA)網絡模型。通過P-NOMA方案，信號相互正交，避免干擾。無人機端利用SIC技術解碼各用戶信號。

1.2 信道模型

無人機與用戶間鏈路可能為視距鏈路，也可能為非視距鏈路，這取決于無人機與用戶間的相對位置。依據文獻[14-15]，用戶與無人機間鏈路呈視距鏈路的概率為：

(2)

式中：φi表示用戶向無人機傳輸信號的仰角,φi=(180/π)arctan(hu/ri)，ri表示用戶離無人機在地面覆蓋區域中心點位置間距離，hu表示無人機盤旋的高度；a,b為環境參數。

路徑衰耗的概率均值為[15]：

(3)

式中：μ1和μ2分別表示視距鏈路和非視距鏈路的路徑衰耗均值；h0表示在1 m的參考距離下的信道增益。

2 問題描述

2.1 上行的P-NOMA的傳輸模型

蜂窩系統中上行鏈路功率控制機制要求來自不同用戶的接收功率均等于目標功率pu。因此，用戶i的傳輸的功率為：

(4)

為了能夠成功地解碼接收的消息，無人機要求不同用戶采用不同功率傳輸消息。為此，用戶先通過正交控制信道，并以相同功率向無人機傳輸各自的控制消息。收到所有用戶的消息后，無人機就依據相應的路徑衰耗值給所有用戶設置解碼順序編號。編號原則為:路徑衰耗值大的用戶，就設置大的解碼編號；反之，路徑衰耗值小的用戶，就設置小的解碼編號。

如圖2所示，無人機通過SIC技術檢測用戶信號[15]。假定無人機覆蓋了J個用戶，用戶U1離無人機最近，用戶UJ離無人機最遠。無人機先解碼信道質量最佳信號，即信道增益最大的信號最先被解碼出來。因此，用戶U1最先被解碼，其解碼編號為1。

圖2 NOMA上行鏈路

當收到解碼編號后，用戶i就利用解碼編號對傳輸功率進行控制：

(5)

式中：δ表示功率衰減因子；n(i)表示用戶i的解碼編號。

各用戶依據各自的功率向無人機傳輸消息后，無人機所接收的信號為：

(6)

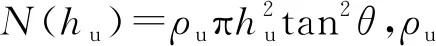
接收了信號后，無人機就依據解碼編號解碼各用戶的信號。在解碼某特定用戶信號時，其他還未解碼的信號對該用戶信號形成干擾，換而言之，僅當前(n(i)-1)用戶的消息被解碼后，才能解碼用戶i的信號。因此，從用戶i接收的信干比(signal interference noise ratio, SINR)為：

(7)

(8)

依據香農公式，用戶i所獲取的速率為：

(9)

2.2 能效

將無人機覆蓋區域面積與無人機所消耗的總能量之比定義為能效：

(10)

Pt(hu)=Pu(hu)+Pc

(11)

式中：Pu(hu)表示無人機盤旋在高度為hu時所消耗的能量,Pu(hu)=αuhu+βu；Pc表示無人機作為無線接入點時所消耗的能量。

2.3 構建目標問題

在滿足無人機高度和用戶服務質量的約束條件下，最大化無人機能效，可構建如式(12)所示的目標優化問題：

(12)

約束項為：

hmin≤hu≤hmax

(13)

(14)

(15)

式(13)對無人機的飛行高度進行限制，式中：hmin,hmax分別表示無人機飛行高度的最小值、最大值；式(14)確保無人機能夠解碼從用戶端所接收的所有消息；式(15)確保了每個用戶均有充足時間向無人機傳輸數據。

3 P1問題的轉換及求解

先將P1問題進行變換，使其都是關于無人機高度的函數，再利用二分法求解。

3.1 P1問題的轉換

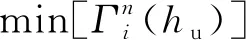
(16)

證明過程為：

將式(5)代入式(7)，可得：

(17)

(18)

當hu=hmin時，Nmin(h′min)=ρuπ(h′min)2tan2θ，將其代入式(16)可得：

(19)

因此，利用命題1，式(14)和式(15)可分別寫成：

(20)

(21)

將式(5)代入式(20)可得：

(22)

再將服務質量約束轉換成高度約束條件：

(23)

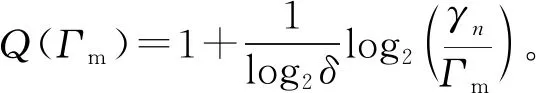
通過上述等式轉換，最終P1問題被轉化成：

(24)

約束項：

(25)

從式(24)可知，P2問題的分子和分母都是關于hu的增函數。

3.2 基于二分法的P2問題的求解

先計算EEn(hu)關于hu的一階微分特性：當hu取hopt時，EEd,n(hopt)=0；當?hu∈(hmin,hopt),則EEd,n(hu)>0；當?hu∈(hopt,hmax)，則EEd,n(hu)<0，其中EEd,n表示EEn的一階微分函數：

(26)

4 性能分析

通過數值評估EEOA算法的性能。仿真參數取值如表1所示。

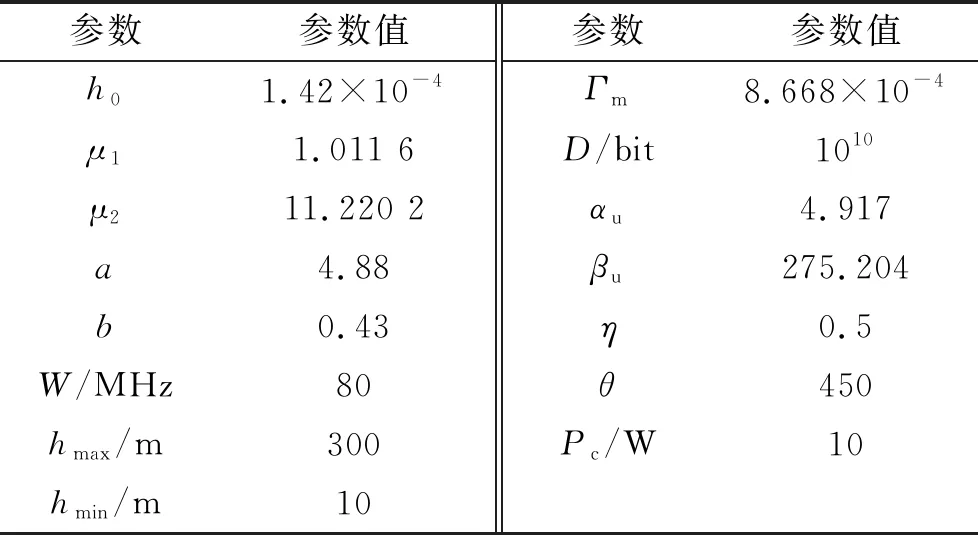
表1 仿真參數取值[16-17]

4.1 基準算法

為了更好地分析EEOA算法性能，選擇均衡正交多接入(orthogonal multiple access, OMA)算法[16]作為參照。在OMA算法中，用戶i所獲取的速率：

(27)

引用命題1，可得到OMA算法的能效：

(28)

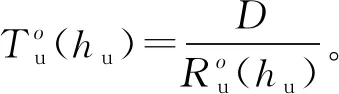
4.2 能效隨飛行高度的變化情況

首先，分析EEOA算法和OMA算法產生的能效，分別依據式(24)和式(28)計算能效，如圖3所示，其中δ=1.5，γn=10。圖中的AEEo(hu)，AEEn(hu)分別表示OMA算法、EEOA算法的能效。

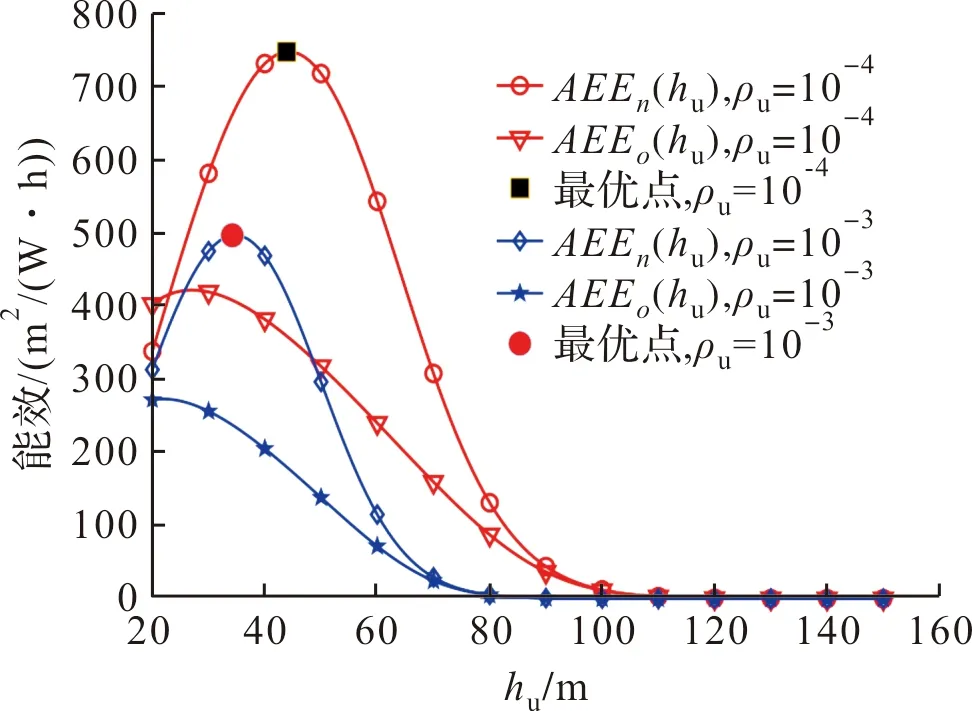
圖3 能效隨飛行高度的變化情況

正如所預料的，獲取最大的能效既不是在最低的飛行高度，也不是在最高的飛行高度。在低的飛行高度期間，能效隨hu的增加而上升，原因在于：依式(24)可知，無人機覆蓋的面積越小，就過度補償了無人機本身能耗的減少。而在高的飛行高度區間，能效隨hu的增加而下降，原因在于：在高的飛行高度區間，無人機需要消耗更多時間去完成數據傳輸，這就增加了無人機的能量消耗。能量消耗量隨飛行高度的增加而增加。

此外，相比于OMA算法，提出的EEOA算法能夠獲得較高的能效。同時，觀察圖3不難發現，OMA算法和EEOA算法的能效隨飛行高度呈鐘形，其最優高度值均可通過算法1獲取。

4.3 最大能效隨用戶密度的變化情況

分析不同用戶密度對能效的影響，如圖4所示，其中γn=6。

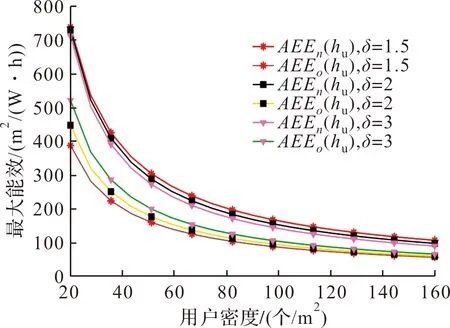
圖4 最大能效隨用戶密度的變化情況

從圖可知，用戶密度的增加，使OMA算法和EEOA算法的最大能效下降。原因在于：用戶密度越大，覆蓋區域內的用戶數越多，這必然增加了無人機的能量消耗，最終就降低了能效的最大值。

此外，相比于OMA算法，EEOA算法的能效性能得到提高。但是隨著δ值的增加，EEOA算法的能效優勢逐步下降。

通過上述分析可知，提出的EEOA算法能夠提高能效。同時，當用戶密度較小時，小的δ值可以獲取更高的能效。

5 總結

針對應急保障通信的無人機作為空中基站的應用場景，提出用戶服務質量約束下無人機能效EEOA優化算法，基于用戶服務質量約束條件，通過優化無人機高度，提升無人機能效。通過構建滿足用戶服務質量約束條件下的目標函數；再經數學處理轉換，形成關于無人機高度的函數；最后，利用二分法求解，得到最優的高度值。仿真結果表明，提出的EEOA算法提升了無人機能效。此外，無人機能效與用戶密度、功率衰減因子成反比。下一步，將重點研究下行鏈路的能效問題以及多個無人機的協同工作。