赤道大洋駐波異常及其年際變化的理論分析

盧姁，趙艷玲，張東凌，張銘，劉賽賽

(1.中國人民解放軍32021 部隊，北京 100094；2.中國人民解放軍31010 部隊，北京 100081；3.中國科學院大氣物理研究所，北京 100029；4.國防科技大學 氣象海洋學院 大氣環流與短期氣候預測實驗室，江蘇 南京 211101)

1 引言

最早研究赤道波系的是Matsuno，由于赤道上Coriolis 參數f為0，但它的導數 β=df/dy在該處又最大，從而使得赤道海域的波動成為海洋動力學中最具有特色的運動[1]。從波動在海洋的傳播看，在赤道海洋，向東傳播的有開爾文波，向西傳播的有羅斯貝波，此外還有高頻的慣性重力波以及特殊的混合羅斯貝重力波，這些構成赤道波系。由赤道波系中的開爾文波和羅斯貝波的調節，可以產生年際變化，并是解釋厄爾尼諾?南方濤動（ENSO）循環的一種機制[2]。因此人們逐漸認識到熱帶大洋中波動的重要性。

Kelvin 首先發現在海洋中有與岸線平行傳播而波形只在岸線附近明顯的波，后來人們就稱之為開爾文波。顯然該岸線的束縛是重要因子。當f隨空間變化時，Matsuno[1]發現，即使沒有該岸線約束，也有類似的波動存在，波形只在赤道附近明顯，但僅有東傳的一支，在此赤道扮演了海岸線的角色。Hirst[3]、Yamagata 和Masumoto[4]從理論上證明了熱帶海氣耦合系統中存在向東傳播的擾動，并認為這是由于東傳的赤道開爾文波所引起的。盧姁和張東凌[5]發現，在長江中下游地區的豐（枯）梅年，熱帶太平洋次表層海溫異常傳播路徑都是沿赤道溫躍層由西向東傳播的，而這有可能與熱帶太平洋上東傳的開爾文波有關。

然而熱帶太平洋有海岸線，向東傳播的開爾文波并不能一直這樣傳播下去，必然會受到海洋東邊界的阻擋而被反射，并有人用此來解釋ENSO 現象[2]。這表明從數學物理上考慮，熱帶大洋的開爾文波不能滿足赤道有界海洋的側邊界條件，其不是該有界海洋的一個解。此時要在赤道滿足該側邊界條件的解則只能是海洋駐波或波包。

有關海洋駐波研究方面，呂新剛等[6]建立了膠州灣潮汐潮流數值模擬及預報的模型，并與實測資料做了對比，發現膠州灣內的潮波以駐波為主。李希彬等[7]依據羅源灣可門水道的25 h 連續走航觀測資料，發現該水道內的潮流為正規半日潮，駐波性質明顯。王春陽等[8]基于2017 年春季和冬季的海流資料分析了廣東紅海灣海域的潮流狀況，發現該海域的潮波介于駐波與前進波之間。Zheng 等[9]利用巡航觀測、衛星高度計數據和理論分析來處理南海的駐波或假潮事件，在2007 年夏季和2009 年，巡航觀測到了南海海盆中的內振蕩信號，信號平均波長為320 km 和390 km，最大振幅為50～100 m，出現水深在500～700 m，最大水深可達1 700 m；衛星高度計圖像及理論分析表明，觀測到的內振蕩屬二維假潮模，其至少持續了2 周，并可在東西長1 000 km，南北寬800 km，水深均勻的海盆假潮模型中獲得；統計分析還表明，從1993年至2012 年中，共有94 個假潮事件。Navas-Montilla等[10]指出，穩定的淺水流通過半封閉海域的出口時，會激發出重力駐波特征模即假潮，他們對此現象做了實驗和數值研究。假潮與海洋駐波類似，也有波腹和波節。以上對海洋駐波和假潮的研究表明，其多發生在封閉和半封閉的海灣和海盆中，水平尺度通常在幾十千米到幾百千米。目前尚未見到寬廣大洋（如太平洋）中的駐波或假潮研究，而開展這方面研究是必要的。

地球上的熱帶大洋無論是太平洋、印度洋還是大西洋，均是有側邊界的。故而實際赤道上滿足該側邊界條件的駐波和波包是否存在，若存在其空間結構和振蕩頻率如何，其與氣候變化有何聯系，這些均是物理海洋學和氣候學中的重要問題。在文獻[11]中，我們得到了有界熱帶大洋的波包解析解并用以解釋熱帶太平洋及印度洋中流場異常復EOF 分析的結果，并對熱帶大洋流場異常的年際和年代際變化以及該波包解與ENSO 及印度洋偶極子（IOD）的關系做了討論[12–14]。不過，用該波包解（前者）卻不能解釋盧姁等[15]得到的春季（4 月份）熱帶太平洋流場異常復EOF 分析第一模態（后者）的結果；后者的空間場呈現向赤道兩側迅速衰減全大洋一致的緯向流，用該第一模態實時間系數做的小波全譜圖上則以6 a 的年際變化最顯著，參見文獻[15]中的圖1b 和圖4b；這樣若用前者模態1（l=1）來解釋，兩者空間分布相一致，但前者振蕩周期為12.2 a，與后者6 a 年際變化相差太遠；若用前者模態2（l=2）來解釋，雖兩者時間變化均約6 a，但空間分布后者為全大洋一致的緯向流，而前者與此相差較大。那么在熱帶大洋是否存在可解釋以上后者的駐波解呢？這是令人感興趣的問題。上面分析也啟示我們，后者可能與赤道駐波密切有關，某些情況下赤道駐波對熱帶大洋流場異常會起重要作用。

圖1 t=0.25T1，n=1 時流場異常的分布Fig.1 Anomalous current distribution at t=0.25T1,n=1

為回答以上問題，并證實上面推斷，本文采用一個理想熱帶大洋模型，在考慮該大洋東、西海岸側邊界條件后，對赤道駐波做了解析求解，以便了解其形態和特點，并對該駐波解與熱帶大洋流場異常的年際變化，以及其與ENSO 和IOD 之間的關系做了討論。

2 數學模型和求解

本文在實數域中討論，計算中采用 m ·kg·s 制。這里設大洋在垂直方向分為均質的上、下兩層，這兩層以躍層為界，這兩層密度分別為常數 ρ1、ρ2，在引入約化重力加速度，不考慮外強迫和摩擦，也不考慮背景流后，則上層海水的控制方程滿足以下赤道 β平面近似下的線性化正壓擾動方程組[11]：

考慮到大洋在x=0和x=L處分別有南北向的西、東海岸，故而u必須滿足以下剛壁邊界條件：

在此L為熱帶大洋東西方向的寬度，x為赤道上距西海岸的距離。

下面來求式（1）至式（3）滿足邊界條件（4）的解析解。為此設u、Φ和v有如下形式：

在此取常數 δ>0，即擾動從赤道向兩極地衰減，而U0、H0設為常數，可視為u、Φ在y=0處的振幅。將式（5）代入式（1）至式（3），可得以下方程組：

現考察式（9），當U0、H0給定后，式（9）等號兩端的表達式均有界；在赤道上因有y=0，故式（9）顯然嚴格成立；在離赤道有些距離處，因ye?δy2→0，式（9）也成立。再考慮到正、余弦函數的絕對值不超過1，及式（9）中的 β=2.289×10?11m?1·s?1其值非常小，而 δ是要待確定的系數。在做了這些考慮后，若確定后的 δ值也非常小，使得式（9）中等號兩端項的量級均非常小，接近于0，則可認為在整個熱帶地區式（9）近似成立（含嚴格成立，以下均做此理解）。如此式（2）也近似成立。式（5）就是式（1）至式（3）的近似解析解。注意到正、余弦函數的絕對值不超過1，則由式（9）可得

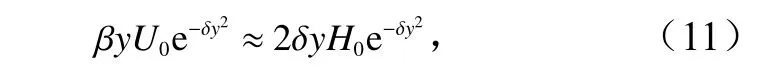
由式（11）知，參數 δ可按以下等式來確定

由式（8）、式（10）可得

此時關于u的邊界條件式（4）可寫為

要滿足以上邊界條件則顯然要有

在此正整數n稱為模態數或模態序號，本文將n=1，2，···的赤道駐波擾動（異常）分別稱為模態1、模態2 等，以避免與我們在流場異常復EOF 分析中的模態[15?16]稱呼（第一模態、第二模態等）相混淆。

式（13）與式（14）必須要兩式相容，由此兩式可得U0=kH0/σ，U0=σH0/()，如此就必須要有k/σ=σ/()，從而可得k2=σ2/，再開方并考慮到式（16）后有

由式（17）可見，頻率 σ與模態數n有關，模態數n越大，頻率 σ就越高。同理，式（12）也可通過與式（13）相容來確定δ，采用以上相同方法可得

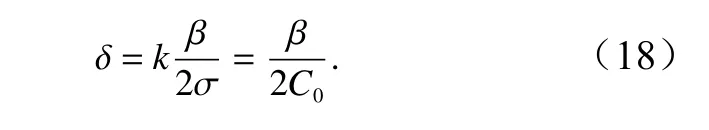
由式（18）中確定的 δ表達式與經典赤道開爾文波解中的相同。現取C0=0.183 m/s（文獻[11]中的取值），則有 δ=6.26×10?11m?2，其值也非常小；這表明式（9）確實近似成立（該近似的精度后文4.1 節中還要詳論）。如此近似滿足式（1）至式（3）以及邊條件（15）的u、Φ為

根據式（14）和式（17）可得H0=C0U0。再令Tn=2π/σ=2L/(nC0)，這里Tn為 模態n的周期，則式（19）、式（20）可寫為

此外還有

這樣式（21）至式（23）即為正壓赤道駐波異常各模態的近似解析解。

3 計算結果分析

3.1 熱帶太平洋的結果

以下給出相應熱帶太平洋的計算結果。熱帶太平洋東西經度相距約160°。取L=17 600 km[11]；取上層海水的標準深度也可認為是熱帶大洋次表層的標準深度；取（ρ2?ρ1）/ρ2為 1 .704×10?5，重力加速度g=9.8 m/s2，則約化重力加速度g′=1.67×10?4m/s2，并有=0 .183 m/s；再取赤道上β=2.289×10?11m?1·s?1，δ=β/(2C0)=6.26×10?11m?2。以上參數均由環境決定，且與文獻[11]中取得相同。再取U0=0.1 m/s并取不同的n值，這樣由式（11）就能得到熱帶太平洋赤道駐波異常的情況。

對n=1，由式（8）知該赤道駐波異常的頻率為σ=3.262×10?8s?1，相應的周期T1=2π/σ=6.10 a。圖1 給出了t=T1/4時該赤道駐波流場異常的情況。圖中橫坐標向東為正，縱坐標向北為正，后同。在整個大洋范圍流場異常只有半波，其經向流異常為0，緯向流異常為全大洋一致的東向流。流場異常在熱帶大洋中部即x=L/2處最大，向赤道南北兩側則迅速衰減，并被限制在赤道兩側約2o的范圍內，其赤道俘獲波的特征十分明晰。在大洋東、西海岸處，流場異常為0，滿足上述邊界條件，且該兩處為駐點。圖2 給出了t=0時該赤道駐波位勢場異常的情況。位勢場異常分別在赤道的東、西海岸處有最大正值、最小負值，在此兩處振幅最大，并向赤道南北兩側迅速衰減。位勢場異常同樣被限制在赤道兩側約2o的范圍內，這點與流場異常相同。大洋中部的x=L/2處則為駐點。位勢場異常在整個大洋也呈半波分布。

圖2 t=0，n=1 時位勢場異常（單位：m2/s2）的分布Fig.2 Anomalous potential field (unit:m2/s2) distribution at t=0,n=1

對n=2，該赤道駐波異常的頻率為σ=6.525×10?8s?1，相 應 的周期T2=3.05 a，其周期為T1的 一 半。圖3 給出了t=T2/4時該赤道駐波的流場異常情況。此時在整個大洋范圍流場異常呈現1 波形態，其經向流異常仍為0，緯向流異常在大洋東部為西向流，西部為東向流。流場異常也向赤道南北兩側迅速衰減，赤道俘獲波的特征也十分明晰。在大洋半寬x=L/2處以及大洋東、西海岸上，流場擾動都為0，該3 處為駐點。圖4 給出了t=0 時n=2赤道駐波的位勢場異常情況。整個大洋中也呈1 波分布態勢；在大洋東、西部x=0至x=L/4 以 及x=3L/4至x=L區段，位勢場異常為正，且在大洋東、西邊界的赤道上振幅最大；在大洋中部x=L/4至x=3L/4區段該異常為負，且在熱帶大洋中部x=L/2處振幅最大。在熱帶大洋東、西邊界以及x=L/2處的最大振幅也向赤道南北兩側作與流場異常類似的迅速衰減。注意參數 δ 與n無關，故在此n=2 的流場和位勢場異常的衰減程度分別與以上n=1的情況相同。

圖3 t=0.25T2，n=2 時流場異常的分布Fig.3 Anomalous current distribution at t=0.25T2,n=2

圖4 t=0，n=2 時位勢場異常（單位：m2/s2）的分布Fig.4 Anomalous potential field (unit:m2/s2) distribution at t=0,n=2

3.2 熱帶印度洋和大西洋的結果

首先給出相應熱帶印度洋的計算結果。熱帶印度洋東西經度相距約70°，可取L=7 700 km[11]。除L和n外，其他參數、g′、C0和 β也均取得與熱帶太平洋的相 同，故 而 δ也 相 同。U0仍 取0.1 m/s。這 樣 在t=T2/4時 取n=1和n=2得到的流場異常和位勢場異常分別與圖1、圖2 和圖3、圖4 形態相同，這樣只需將該4 張圖的橫坐標標定為0～77（×100 km），就可得到熱帶印度洋的相應圖像，故此圖略。兩者不同之處僅在于熱帶大洋寬度不同，兩者駐波異常的頻率 σ不同，從而周期也不同。當取熱帶印度洋n為1 和2 時，相應的周期分別為2.67 a 和1.33 a。

接著給出熱帶大西洋的結果。熱帶大西洋東西經度相距約45°，約合4 950 km，可取L=5 000 km[11]。與熱帶印度洋同理，此時只需將圖1 至圖4 的橫坐標標定為0～50（×100 km）就能得到相應的圖像（圖略）。此時取n為1 和2 時，其相應的周期分別為1.73 a和0.87 a。

4 有關駐波解的討論

4.1 駐波解的近似精度

將式（5）、式（6）代入式（2）后可得式（9），這樣該解滿足式（2）的問題就轉化為滿足式（9）的問題。式（9）還可寫為

式中，ε本應恒為0，這表示該方程嚴格成立。若該方程近似成立時，則 |ε|值就反映了本文近似解的誤差大小，即該近似解的精度。由式（19）知 β=2δC0，將其代入式（24）后可得

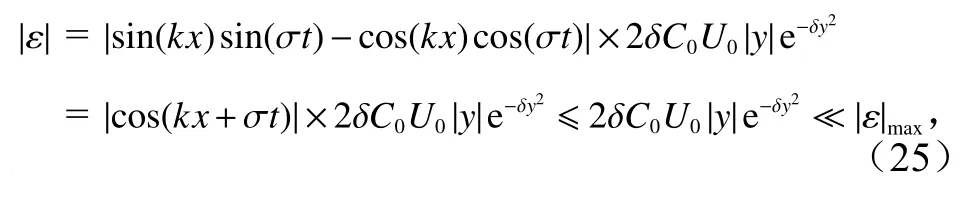
式中給出了可能出現的極大誤差 |ε|max沿 經向（y方向）的分布。為此對上述給定的δ、C0、U0值做了計算，圖5a給出了該誤差 |ε|max沿經向的分布，并可見該誤差在距赤道約100 km 處的值最大，約為1 .3×10?7m/s2，并具有加速度的量綱。本文用的計量系統為 m ·kg·s制，對此制式的相對誤差為 1.3×10?7(m/s2)/(1 m/s2)=0.000 013%，非常小。再者可取g′=1.67×10?4m/s2作為加速度的特征尺度，而對該特征尺度的相對誤差為1.3×10?7(m·s2)/g′=0.08%，也很小。這樣式（9）確實近似成立，且近似精度還較高，故而解析解式（21）至式（23）確實是式（1）至式（3）具有較高精度的近似解。

圖5 | ε|max（a）、| u|max（b）和 | Φ|max（c）沿經向的分布Fig.5 The distribution of | ε|max (a)、| u|max (b)和 | Φ|max (c) along lon gitude

4.2 駐波解的空間結構和時間演變

該赤道駐波異常向赤道南北兩側的衰減快慢，這取決于值 δ=β/(2C0) 的 大小，因赤道上 β 是常數，故 δ值僅反比于越小則該駐波向赤道南北兩側衰減得越快。實際在以上三大洋中，雖和 (ρ2?ρ1）/ρ2會有些差異，但總體相近，故C0總 體也應相近，為此本文中對C0值也取得相同，故而 δ的取值也相同，這表明該駐波異常向赤道南北兩側的衰減程度也相同。圖5b，圖5c 分別給出了模態1 的u在t=T/4 時 在大洋中心線x=L/2處的經向分布，以及 Φ 在t=0時 在大洋西邊界x=0處的經向分布。從圖5b，圖5c 上可見u、Φ的 最大振幅 |u|max、|Φ|max從赤道到極地的衰減程度以及該振幅被赤道所俘獲，從而被限制在赤道南北各200 km 也即約2°的范圍內。因δ與模態數n無關，故模態2 的情況與模態1 相同。注意到本文的 δ=β/(2C0)，與經典赤道開爾文波的表達式相同，故該駐波異常被赤道俘獲的情況也與之相同。

模態1（n=1）在整個大洋只有半個波（圖1，圖2），其波長為赤道上整個大洋寬度的2 倍；模態2 在整個大洋有1 個波（圖3，圖4），其波長則為赤道上整個大洋的寬度；余類推。n越大，即模態數越高，該駐波的波長則越短。由式（17）可知，熱帶大洋的寬度L越寬，模態數n越低，則其頻率越低，模態1 的頻率最低，此時其波長也最長。與之相應，頻率越低的波動其周期越長。從上述計算結果看，以上三大洋的赤道駐波異常模態1、模態2 的周期均接近或處在年際振蕩周期之內。

圖6a，圖6b 以及圖7a，圖7b 分別給出了模態1、模態2 赤道上的流場以及位勢場在時刻0、T/8、T/4、3T/8、T/2、5T/8、3T/4 和7T/8 的空間分布，圖中以熱帶大洋寬度L作為1 個單位，模態1、模態2 的周期T分別取為T1、T2。這些圖可清楚揭示流場與位勢場異常隨時間變化的駐波振蕩以及駐點的分布，并豐富了第3 節中的論述。模態1 以及模態2 的流場異常在時段t∈(0,T/2)（在此T取T1或T2，下同），分別在整個大洋有東向流以及在左半大洋有東向流，右半大洋有西向流；在時段t∈(T/2,T)，則模態1 以及模態2 的流向各與前一時段流向相反；如此隨時間周而復始（圖1，圖3 和圖6a，圖6b）。模態1 及模態2 的位勢場異常在時段t∈(0,T/2)，分別有整個大洋西半部為正異常，東半部為負異常以及在x∈(0,L/4)和x∈(3L/4,L)區間有正異常，在x∈(L/4,3L/4)區 間有負異常；在時段t∈(T/2,T)，則模態1 以及模態2 位勢場異常則各與前一時段異常符號相反，如此周而復始，并以位勢場駐點為支點在其兩側呈現蹺蹺板變化（圖2，圖4 和圖7a，圖7b）。比較圖1 至圖4 和圖6，圖7 還可見，對各模態流場與位勢場異常的配置具有 π/2的位相差，當流場異常為0 時，位勢場異常絕對值最大，反之亦然，位勢場異常位相要超前流場異常 π/2。

圖6 模態1（a）、模態2（b）中流場異常隨時間分布Fig.6 Anomalous current distribution at different time in mode 1 (a) and mode 2 (b)

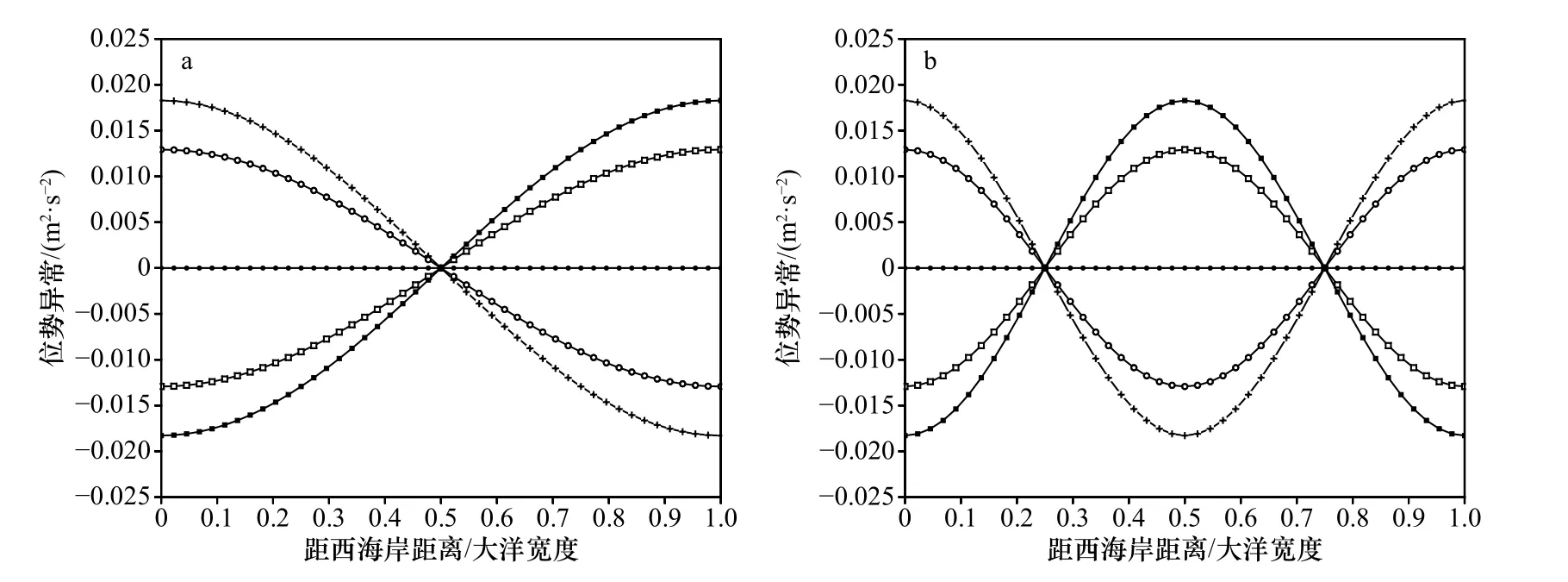
圖7 模態1（a）、模態2（b）位勢場異常（單位：m2/s2）隨時間的分布Fig.7 Anomalous potential field (unit:m2/s2) distribution at different time in mode 1 (a) and mode 2 (b)

4.3 與熱帶大洋流場異常模態的比較

現與實際熱帶太平洋流場異常的統計動力診斷結果做比較。引言中已提及，我們曾對多年熱帶太平洋冬、春、夏、秋季（以1 月、4 月、7 月、10 月份為代表）的流場異常做過復EOF 分析（前者）[15]，發現本文3.1 節中取模態1 計算得到的熱帶太平洋駐波異常（后者）的流場分布，其與前者流場異常第一模態的空間場分布十分一致；該模態流場異常在整個太平洋的赤道上及臨近赤道處，均表現為同一方向的緯向流，而幾乎無經向流；并大體位于赤道兩側南北緯5°之內，即該模態為赤道所俘獲（參見文獻[15]中圖1）。后者的振蕩周期如上所述為6.10 a，這正處于ENSO 3～7 a的年際變化內。在對前者第一模態做的實時間系數小波分析中，發現冬、春、夏、秋季該模態3～7 a內的年際變化均很顯著。特別在春季（4 月份）前者第一模態約6 a 的年際變化是最顯著的，其顯著性大大超過了年代際變化，而其他3 季則反之（參見文獻[15]中圖4），并與后者模態1 的周期6.1 a 十分相近。這樣引言中提到用波包解[11]不能解釋的春季（4 月份）熱帶太平洋流場異常復EOF 分析第一模態的結果現在則可通過本文模態1 的駐波解來完美解釋，故而該赤道駐波異常在熱帶太平洋中的確存在。盧姁等[15]還提出前者的第一模態是ENSO 的主要模態，本文這里則要強調的是，該文獻中第一模態（異常）正是模態1 的赤道駐波異常，如此該駐波（異常）在ENSO 中的作用不能忽視，其對熱帶太平洋年際氣候異常的貢獻也應予以肯定。

再與實際熱帶印度洋流場異常的統計動力診斷結果做比較。我們也曾對熱帶印度洋10 月份的流場異常做過復EOF 分析（前者）[13]，該月份是印度洋偶極子（IOD）表現最明顯的月份。本文3.2 節中取熱帶印度洋寬度并取模態1 計算得到的赤道駐波異常（后者）的流場分布，也與前者第一模態表層空間場的分布一致，該空間場在整個印度洋中為一致的緯向流，經向流十分小，且也為赤道所俘獲（參見文獻[13]中圖2a）。后者的振蕩周期如上所述為2.67 a，并處于IOD 的2～4 a 的年際變化周期內。在該文獻中提出了前者第一模態與IOD 模態相吻合，但那里未討論第一模態的物理本質。本文要補充的是，前者第一模態的物理本質也是模態1 的熱帶印度洋駐波異常，其與IOD 密切相關，并對熱帶印度洋氣候異常的年際變化產生影響。

我們還對熱帶太平洋和印度洋做過一些流場復EOF 分析工作，以討論實際熱帶大洋上層流場異常第一模態與氣候異常之間的關系，如：長江流域梅雨豐欠[12]、兩類ENSO[17]、熱帶印度洋WYRTKI 急流和亞洲熱帶夏季風[18]、印度洋冬季風及其環流等[14–16]。發現本文模態1 的赤道駐波與這些文獻中有些流場復EOF分析的第一模態形態相似，本文模態1 的周期也與有些第一模態的年際變化相一致。這表明，本文赤道駐波異常解與這些文獻所研究的有些氣候現象關系密切，可能也是這些現象的生成機制之一。

因我們未對熱帶大西洋流場異常進行復EOF 分析，故這里無法對熱帶大西洋駐波異常做詳細討論。不過文獻中通過船舶資料的主分量分析得到熱帶大西洋上層海溫異常的第一主分量最大值出現在赤道上，其具有準兩年的年際變化[19]，這與本文在3.2 節中取模態1 得到的熱帶大西洋赤道駐波異常周期為1.73 a，兩者在年際變化上則有相似之處。

4.4 與熱帶大洋波包解的比較

Zhang 等[11]求出了熱帶大洋中的波包解（前者），現將本文的赤道駐波解（后者）與前者相比較，兩者均采用同樣的赤道 β平面近似下的線性化正壓擾動方程組，所取的環境參數也相同，僅流場振幅取得不同。而在線性化模式中振幅不會影響解的空間形態分布和時間演變。

兩者的相同之處在于：解均為緯向流，無經向流；該緯向流均為赤道所俘獲，解向赤道南北兩側衰減的程度也相同。大洋東、西邊界均是兩者的駐點，當模態數高于1 時大洋內部也有駐點。兩者的頻率均正比于模態數以及經典開爾文波的相速C0，而反比于熱帶大洋寬度L。比較本文的圖6 與前文的圖1 和圖4知，兩者不同之處在于：兩者空間形態及其隨時間的演變有所差異。如本文模態1 所有時刻在整個大洋均為一致的緯向流，而前文模態1 雖大部份時刻都是這樣，但也有時刻例外。這種差異導致兩者頻率有所不同。從物理上考慮，波動能量與頻率呈正相關。前者波動振幅極值處會隨時間向左右水平擺動，這會消耗能量，而后者是駐波，無此擺動。若兩者能量相同，前者此擺動所需的能量就體現在后者頻率的增加上，故后者頻率要高于前者。在兩者頻率的表達式中，當模態數、C0和L取得相同時，前者的頻率只有后者一半，前者的周期則為后者一倍，從而相應于前者的年際變化和年代際變化要較后者的更長。

本文與前文中都討論了兩者在熱帶大洋異常中的表現和作用。這里要指出，前者與后者并不相互排斥，而是相互補充，并都能解釋某些特定的海洋、氣候事件。如對ENSO，其冬、春季節的流場異常分布更接近本文的模態1；伴隨厄爾尼諾的發生，熱帶中太平洋海洋上層會有海溫強正異常東傳，而這又類似前文模態2 中位勢異常的傳播形態；注意到該兩者的周期又都落在ENSO 其3～7 a 的年際變化中，故而ENSO 可能與這兩者都密切有關，而并非前文所述僅與前者有關。IOD 的情況也是如此。后者因周期較短，更有利于解釋海洋異常的年際變化，而前者則更容易解釋年代際變化。在實際熱帶大洋中，兩者可同時存在，并各自發揮影響。ENSO 和IOD 都是復雜的海氣相互作用事件，不能僅用兩文的簡單模型來完全概括和描寫；也許兩文分別能解釋ENSO 和IOD 中的不同類型。

本節有關赤道駐波解的討論表明，赤道駐波異常在實際大洋中的確存在，其還與ENSO、IOD 以及其他氣候事件關系密切[20–21]，可能是其形成機制之一并產生影響；而本文能提供ENSO 和IOD 等研究的新思路，故而還是很有價值和值得肯定的；為此對赤道駐波異常做更深入的研究是十分必要和必須進行的。

5 結語

本文采用赤道 β平面近似下的線性化正壓擾動方程組，引入約化重力加速度后，在滿足走向南北的東西海岸剛壁邊界條件下，求得了大洋赤道駐波異常的近似解析解，給出了該解的計算結果，并與實際熱帶太平洋和印度洋的流場異常做了比較。本文得到的主要結論如下：

（1）赤道駐波異常模態1 的流場異常在整個大洋為半波，為方向一致的緯向流，無經向流；流場異常在熱帶大洋中部最大，并向赤道南北兩側迅速衰減，其被限制在赤道南北兩側約2o的范圍內。

（2）赤道駐波異常模態2 的流場異常在整個大洋為1 波，在大洋東、西部分緯向流的流動方向相反，也無經向流；流場異常向赤道南北兩側的衰減情形與模態1 同。

（3）決定赤道駐波異常向赤道南北兩側衰減程度的系數，其僅與約化重力加速度和上層海水標準深度之乘積的平方根，即經典赤道開爾文波的相速成反比；當該相速相同時，該駐波異常向赤道兩側的衰減也相同。

（4）赤道駐波異常的振蕩頻率其與模態數成正比，與熱帶大洋寬度成反比；模態數越低，熱帶大洋寬度越大，則該頻率越低，相應振蕩周期越長；模態1 的振蕩周期最長。

（5）取各參數為典型值及模態數為1，再取熱帶太平洋和印度洋的寬度，計算表明，兩者赤道駐波流場異常都與實際流場異常復EOF 分析得到的第一模態空間分布和年際變化相一致；這表明此復EOF 第一模態的本質是赤道駐波異常，并是太平洋ENSO 和印度洋IOD 的形成機制之一。

最后要說明的是，因本文屬理論工作，對模型做了必要簡化和近似，所取參數雖大體符合實際，但也不完全相同，這些都會使本文的計算結果與實際在總體一致的情況下，還存在某些差異，這也是正常及可以理解的。