用活動開啟數學探究之旅
——《數學廣角——鴿巢問題》教學解讀

○田麗娟

【課前思考】

特級教師吳正憲提出：給學生“好吃又有營養”的數學。課堂上教師要保護學生探求未知領域的好奇心，關注學生的體驗活動，尊重每一個孩子的個性，因為學習興趣是學生持久發展的動力源泉。“鴿巢問題”作為“數學廣角”的內容，必然有一個抽象、推理和建模的過程，那么，該如何教給學生“好吃又有營養”的數學呢？本節課我主要從以下四個方面來思考：

1.學什么？感悟數形結合、數學模型的思想，掌握解題方法。

2.怎么學？學生的學習過程應當是生動、豐富、富有生命力的過程。在經歷探究鴿巢問題的過程當中，學生通過游戲、觀察、猜測、實驗、推理等實踐活動來學習新知識，獲得解決問題的方法。

3.如何保證學生的課堂主體地位？以生為本，給予學生足夠的時間和空間思考、探索、交流。

4.如何調動學生的積極性？學習環節形式多樣，運用游戲、視頻等激發學習興趣，豐富學生的認知。

【教學流程】

1.游戲導入，激發探究興趣。

玩4 個同學搶坐3 個凳子的游戲。游戲結束后提問：游戲很好玩，但是學會思考游戲背后的道理很重要。4 個人搶3 個凳子出現了什么情況？引導學生認識到：因為凳子數比人數少1，所以總是有1 個凳子上坐了2 位同學。引出課題：這就是我們今天所要研究的問題——鴿巢問題。

【設計意圖】課堂伊始從學生喜歡的游戲活動入手，設置懸念，關注學生的活動體驗，有利于激發學生探究問題的興趣和好奇心。

2.呈現問題，確定探究方向。

課件呈現：把4 支鉛筆放進3 個筆筒中，那么總有1 個筆筒里至少有2 支鉛筆。理解“總有”和“至少”的意思。教師追問：你覺得這句話說得對嗎？可用擺一擺、畫一畫、寫一寫等方法把自己的想法表示出來。

3.合作學習，經歷探究過程。

（1）以小組為單位展示交流探究成果。

方法一：枚舉法證明。

小組同學邊演示邊講述，同時用自己的方式進行記錄。預設：學生通過動手擺一擺呈現有4種方法，指導學生邊擺放邊記錄。教師追問：在這需要考慮順序嗎？引導學生只考慮存在性，不考慮順序。

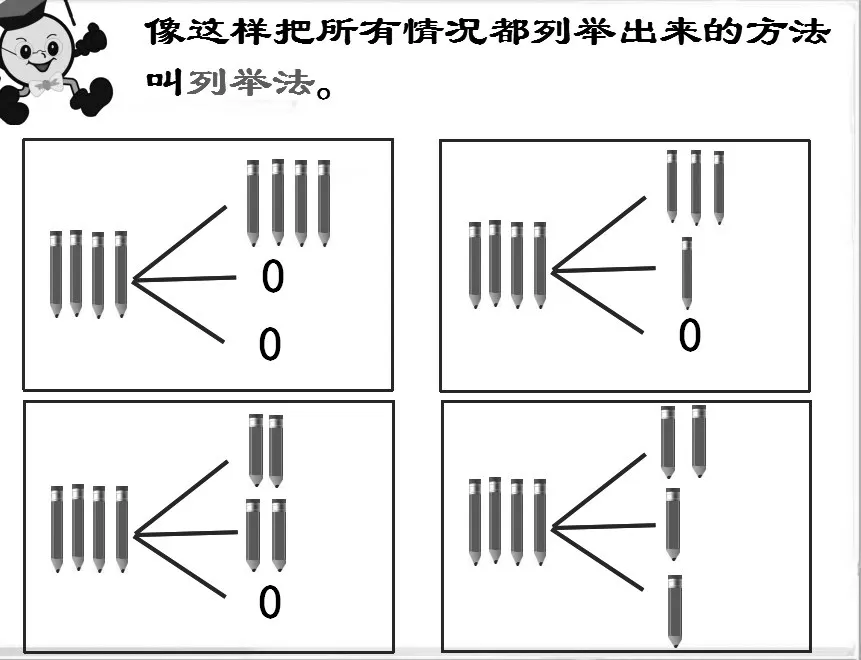
教師引導：觀察以上4 種不同的放法，為什么說“總有1 個筆筒里至少有2 支鉛筆”？學生結合具體擺法說明其中的道理。追問：至少放進2 支鉛筆就是最少是2 支，比2 支多可以嗎？把符合要求的筆筒或數據用彩筆標出，深入理解“總有1個筆筒里至少有2 支鉛筆”的含義。預設：可能有學生把4 進行分解，共有4 種情況（4，0，0），（3，1，0），（2，2，0），（2，1，1）。引導學生邊板書邊講解分的過程。

方法二：假設法證明。

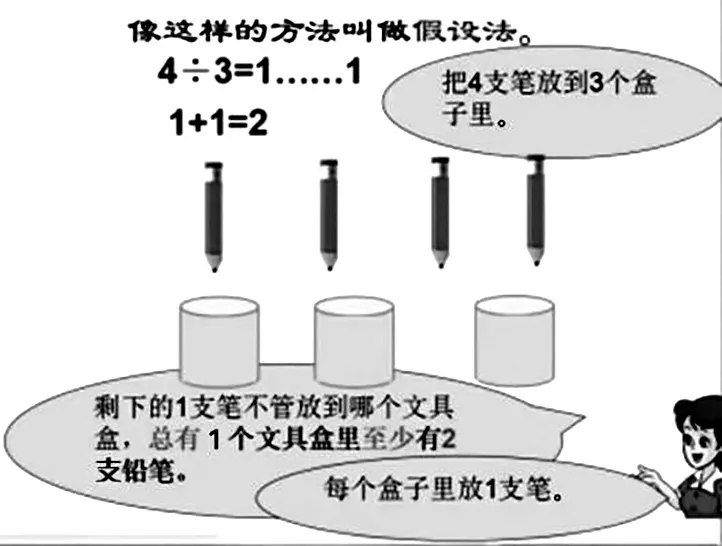
像剛才這樣把所有的情況都列舉出來的方法在數學上叫“枚舉法”，也叫“列舉法”。引導學生回憶學習雞兔同籠問題時用到的“假設法”，啟發學生嘗試用“假設法”解決今天的問題。讓學生在小組內說一說，交流自己的想法，然后以小組為單位全班交流。教師適時點撥：假設先在每個筆筒里放1 支鉛筆，3 個筆筒里就放了3 支鉛筆。還剩下1 支鉛筆，放進任意一個筆筒里，這個筆筒里就有2支鉛筆。學生通過操作或畫圖，直觀感受這種“假設先在每個筆筒里放1 支鉛筆”的結果。

追問：你為什么要先在每個筆筒里放1 支鉛筆呢？平均分的好處是什么？引導學生認識到平均分就可以使每個筆筒的筆盡量少一點，也就可能找到和題目中的意思不一樣的情況。教師啟發：到現在為止，你有什么發現？能得出什么結論？學生能夠深入理解“把4 支鉛筆放進3 個筆筒中，總有1個筆筒里至少有2 支鉛筆”的原理。

【設計意圖】學生學習數學的過程充滿了觀察、實驗、猜想、驗證、推理與交流等豐富的學習活動，學生只有在數學活動中才能對問題的研究深入。學生根據自己的猜想反復地實驗驗證鴿巢原理，動手操作有利于學生對此類問題的理解。對“假設方法”的探究是學生更高層次的學習，教師的引導、生生之間的交流與辯論是開啟深度思維的途徑。

4.深度探究，構建數學模型。

現在老師把題目改一下，同學們思考剛才的結論還成立嗎？

（1）把5 支鉛筆放進4 個筆筒中，總有1 個筆筒里至少放進幾支鉛筆，為什么？

（2）如果6 支鉛筆放進5 個筆筒中，那么總有1 個筆筒里放進（ ）支鉛筆。

（3）把10 支鉛筆放進9 個筆筒中呢？如果把100 支鉛筆放進99 個筆筒中呢？你發現了什么規律？

教師引導學生得出一般性結論：只要放的鉛筆數比筆筒的數量多1，總有1 個筆筒里至少放進2 支鉛筆。對不同解決問題的方法進行比較，感受枚舉法的優越性和局限性，感悟假設法更具有一般性。

追問：假如有5 支鉛筆放進3 個筆筒里，會出現什么情況？總有1 個筆筒里至少放進幾支鉛筆？先猜想，再驗證。這個問題學生容易犯“總有1個筆筒里至少放進3 支鉛筆”的錯誤，讓學生發現問題，引發討論，促進知識的理解和掌握。教師引導：怎樣把規律用算式表示出來？展示交流后總結：至少數=商+1。

小結：這就是最簡單的“抽屜原理”，可以概括為：把多于m個物體任意放到m個抽屜里，那么總有1 個抽屜中至少放進了2 個物體。回顧課堂開始的游戲，說說“搶凳子”游戲中包含的數學知識。

【設計意圖】數學模型的建立是一個不斷感知、積累的過程。通過問題數據的增大，學生進行大膽而合理的推理、驗證，進而從生活實際走向數學建模。這一環節突出數學建模的過程，體現學習“有營養”的數學的意義所在。

5.微視頻形式展示鴿巢問題的歷史文化資料。

展示數學小知識鴿巢原理、抽屜原理的由來，采用微課的方式介紹德國數學家狄利克雷和他的“抽屜原理”。

【設計意圖】數學文化作為教材的組成部分,應滲透在整套教材中。通過探究，學生感受到本課所發現的規律和科學家發現的有關，增加探究的成就感。同時了解到“鴿巢原理”最初的模型和在生活中的廣泛應用，增加數學文化氣息。

6.運用知識，解決實際問題。

（1）用學到的知識解釋教材中撲克魔術的原理：一副撲克，取出大小王，還剩52 張牌，5 人每人隨意抽一張，我知道最少有2 張牌是同花色的。為什么？

（2）張叔叔參加飛鏢比賽，投了5 鏢，成績是41 環，張叔叔至少有1 鏢不低于（ ）環。

（3）隨意找13 位老師，他們中至少有2 個人的屬相相同。為什么？

【設計意圖】學生學到的知識要更好地納入知識體系。通過梯度練習，鞏固所學知識，培養學生解決實際問題的能力，感受學習數學的價值和解決問題的快樂。