基于數學建模思想的“解三角形的應用”教學設計

刁志瑞 葉慧妍 盧 韞

[摘 ?要] 基于以往“解三角形應用”課堂中容易出現例子斷裂分割，缺乏聯系而造成的學習障礙，文章將重新從數學建模的視角，通過設計完整的探險故事，在問題解決的過程中整體聯系解三角形應用模型，從而培養學生的建模意識和建模能力.

[關鍵詞] 數學建模;解三角形的應用;解三角形;教學設計

《普通高中數學課程標準（2017版）》提出重視培養學生的六大數學核心素養：數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析. 數學建模是對現實問題進行數學抽象，用數學語言表達問題、用數學方法構建模型解決問題的素養，也是數學學習過程中學生需要掌握的重要思想和能力. 數學建模構建了數學與現實世界的橋梁，是數學應用于生活，生活聯系數學的重要形式. 因此，在數學教學中有意識地基于數學建模思想設計課程，將有助于讓學生感悟數學與現實世界的關聯，進一步感受數學的應用價值，體會數學的應用之美;同時利用數學建模過程充分發展學生分析問題和解決問題的能力，培養其良好的數學素養.

“解三角形的應用”與現實生活有著密切聯系. 如何能夠將數學建模思想貫穿于課程中，又不顯得與生活脫節而無趣呢？為此，本文將基于數學建模思想，在“解三角形的應用”一課中，通過創設有趣、完整的探險故事，統領解三角形應用的幾種數學模型，讓學生能夠在“問題解決中學習”，實現在課程中培養建模思想和建模能力的目標.

教材分析

天文觀測、航海和地理測量是人類認識自然的重要方面，而解三角形的理論在其中發揮了重要作用. 同時，數學發展歷史上，受到天文測量、航海測量和地理測量等方面實踐活動的推動，解三角形的理論也得到不斷發展，并被用于解決許多測量問題. 在初中，我們已經能夠借助于銳角三角函數解決有關直角三角形的一些測量問題. 然而在實際工作中我們還會遇到許多其他的測量問題，這些問題僅用銳角三角函數就不夠了，如：怎樣在航行途中測出海上兩個島嶼之間的距離？怎樣測量底部不可到達的建筑物的高度？這些問題的解決需要應用本章學習的正弦定理與余弦定理.

本節內容選自人教A版高中數學必修五第一單元1.2節“解三角形應用舉例”. 《普通高中數學課程標準（2017版）》指出“能用余弦定理、正弦定理解決簡單的實際問題”，因此本節解三角形的應用是在前面正弦、余弦定理學習的基礎上進一步把其遷移到實際問題的重要知識，是實際問題與數學知識相結合的典型案例，能夠充分體現數學建模在實際問題中的優勢和力量，是培養學生數學抽象、數學建模的重要教學內容.

學情分析

1. 認知基礎

本節課針對成績中等偏上的學生設計，在這之前學生已經學習過三角函數的誘導公式、正弦定理和余弦定理，對這些內容有比較透徹的理解，并且經過高中數學的學習，已經積累了一定的數學活動經驗，具備一定的數學抽象能力.

2.認知障礙

雖然已經掌握正弦定理與余弦定理，但學生對于實際問題中解三角形的應用還不熟悉，對于現實問題的抽象與三角形模型的構建存在一定困難，數學建模能力有待進一步加強.

教學目標

1.知識與技能：了解解三角形在實際生活中的廣泛應用;能夠利用解三角形相關知識構建數學模型解決常見的實際問題.

2.過程與方法：通過講故事的學習形式，在解決實際問題的過程中感受解三角形應用的價值，感知數形結合、分類討論和數學建模的思想方法，豐富數學建模與活動經驗.

教學重難點

1.教學重點：解三角形的應用.

2.教學難點：實際問題中解三角形的建模方法.

教學過程

1. 復習引入

師：在之前的課程中，我們學習了正弦定理、余弦定理及其證明，也鼓勵大家課下積極探索多樣的證明方式. 下面，我們首先復習一下這兩個定理.

正弦定理：在一個三角形中，各邊和它所對角的正弦的比相等，即==.

余弦定理：三角形中任何一邊的平方等于其他兩邊的平方和減去這兩邊與它們的夾角的余弦的積的兩倍，即a2=b2+c2-2bccosA，b2=a2+c2-2accosB，c2=a2+b2-2abcosC.

師：事實上，正弦定理和余弦定理在實際測量中有許多應用，尤其是古代. 下面，讓我們回到古代，使用古人的工具（測角儀和皮卷尺）來感受這兩個定理的魅力.

2. 情境探究

時間回到古代，這時候按照藏寶圖，你帶著測角儀、皮卷尺和指南針來到了一座小島上. 接下來，你將根據藏寶圖的指示，靈活使用手中的測量工具去尋找寶藏. 藏寶圖顯示，尋寶的起點是一棵有特殊標記的高大樹木. 經過比對，你走到了這棵樹的旁邊，打開了藏寶圖……

指示1：（例題）請沿西南方向走一段距離，該距離為兩倍樹木高度，走過這段距離，你將看到一個瞭望臺.

師：憑借手中的指南針，我們可以確定下一步走的方向，但如何用測角儀、皮卷尺測量樹高呢？（給出示范，如圖2）

師：測角儀可以測出視角，皮卷尺可以測出你與樹木之間的距離，這樣就構成了已知一個銳角和一條直角邊的直角三角形，根據l1=d1·tanα求出樹木高度. 我們稱這種高度測量為“底部可到達”.

設計意圖：本題屬于解三角形中的基礎題型，主要目的是通過演示和簡單講解，讓學生熟悉情境，并利用情境中已有的工具測量樹高，了解實際情境中解三角形的應用概況，構造三角形，尋找已知量. 本題只需要根據樹木與地面垂直的隱含條件構造一個直角三角形即可求解，是高度測量中底部可到達的最容易的類型，用于熟悉情境和引入相對恰當.

指示2：請測量瞭望臺頂部高度，并向東走一段距離，該距離為五倍瞭望臺頂部高度. 在那里，你將隔著海面看到一座燈塔.

師：與上一個指示類似，這時你依然可以走到瞭望臺旁，但你需要測它的一部分高度，這種情況下，僅構造一個三角形夠嗎？請同學們動手試一試. 完成的同學可以上臺演示你的做法.

此時，需要構造兩個直角三角形，l2=d2（tanγ-tanβ）.

設計意圖：本題屬于解三角形中的基礎題型，代表了高度測量中的“底部可到達”，但未知量是建筑中的一部分，是第一個例題的變式，此時需要選擇. 此題依然不涉及復雜的推理過程，相對容易，主要目的是讓絕大多數學生體會從實際情境中構建數學模型的數學抽象過程，并初步使用情境中給出的工具，體會測量中的數學，感受數學知識的應用價值.

指示3：請你測量燈塔的高度，并沿著海岸向南走一段距離，該距離為三倍塔高. 在那里，你將隔海看到一艘游輪.

師：此時，我們已經不能測出燈塔與自己的距離. 要如何轉化呢？需要構造幾個三角形呢？請同學們4人一組，進行討論. 有想法的小組可以演示.

此時需要構造兩個直角三角形，根據三角形中的兩個等量關系可以求出兩個未知量，其中一個即為塔高l3. （m1+d3）tanα2=m1tanα1？圯m1=？圯l3=.

設計意圖：本題為測高度的第三種類型——底部不可達，相對前面兩題難度有提升. 仍需要構造兩個直角三角形，但此時觀察者不再是站在原地改變視角，而是通過改變自己的位置，創造出多個已知量，進一步解決問題. 這一情境是上一題的變式練習，通過這一問題，學生對從實際問題出發構造三角形應有更深刻的認識.

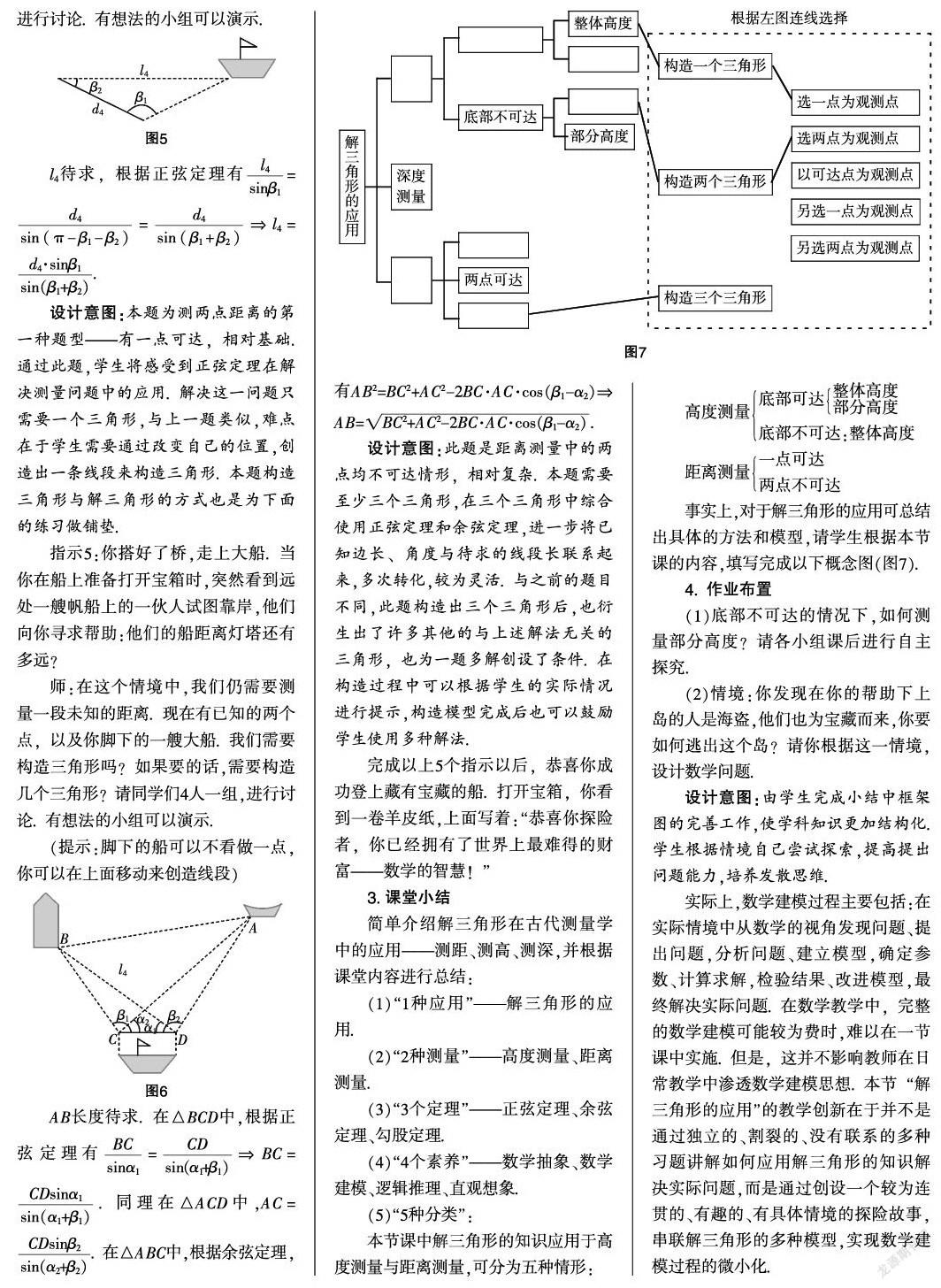
指示4：你現在可以看到一艘大船了嗎？恭喜，你已經離寶藏很近了——它就在船上. 但你還需要測量出船到岸邊的距離，來搭建一個上船需要的橋，你會怎么做呢？

師：在這個情境中，我們需要測量一段未知的距離. 現在僅有兩個點，我們需要構造三角形嗎？如果要的話，需要構造幾個三角形？請同學們4人一組，進行討論. 有想法的小組可以演示.

l4待求，根據正弦定理有==？圯l4=.

設計意圖：本題為測兩點距離的第一種題型——有一點可達，相對基礎. 通過此題，學生將感受到正弦定理在解決測量問題中的應用. 解決這一問題只需要一個三角形，與上一題類似，難點在于學生需要通過改變自己的位置，創造出一條線段來構造三角形. 本題構造三角形與解三角形的方式也是為下面的練習做鋪墊.

指示5：你搭好了橋，走上大船. 當你在船上準備打開寶箱時，突然看到遠處一艘帆船上的一伙人試圖靠岸，他們向你尋求幫助：他們的船距離燈塔還有多遠？

師：在這個情境中，我們仍需要測量一段未知的距離. 現在有已知的兩個點，以及你腳下的一艘大船. 我們需要構造三角形嗎？如果要的話，需要構造幾個三角形？請同學們4人一組，進行討論. 有想法的小組可以演示.

（提示：腳下的船可以不看做一點，你可以在上面移動來創造線段）

AB長度待求. 在△BCD中，根據正弦定理有=？圯BC=. 同理在△ACD中，AC=. 在△ABC中，根據余弦定理，有AB2=BC2+AC2-2BC·AC·cos（β1-α2）？圯AB=.

設計意圖：此題是距離測量中的兩點均不可達情形，相對復雜. 本題需要至少三個三角形，在三個三角形中綜合使用正弦定理和余弦定理，進一步將已知邊長、角度與待求的線段長聯系起來，多次轉化，較為靈活. 與之前的題目不同，此題構造出三個三角形后，也衍生出了許多其他的與上述解法無關的三角形，也為一題多解創設了條件. 在構造過程中可以根據學生的實際情況進行提示，構造模型完成后也可以鼓勵學生使用多種解法.

完成以上5個指示以后，恭喜你成功登上藏有寶藏的船. 打開寶箱，你看到一卷羊皮紙，上面寫著：“恭喜你探險者，你已經擁有了世界上最難得的財富——數學的智慧！”

3.課堂小結

簡單介紹解三角形在古代測量學中的應用——測距、測高、測深，并根據課堂內容進行總結：

（1）“1種應用”——解三角形的應用.

（2）“2種測量”——高度測量、距離測量.

（3）“3個定理”——正弦定理、余弦定理、勾股定理.

（4）“4個素養”——數學抽象、數學建模、邏輯推理、直觀想象.

（5）“5種分類”：

本節課中解三角形的知識應用于高度測量與距離測量，可分為五種情形：

高度測量底部可達整體高度部分高度底部不可達：整體高度

距離測量一點可達兩點不可達

事實上，對于解三角形的應用可總結出具體的方法和模型，請學生根據本節課的內容，填寫完成以下概念圖（圖7）.

4. 作業布置

（1）底部不可達的情況下，如何測量部分高度？請各小組課后進行自主探究.

（2）情境：你發現在你的幫助下上島的人是海盜，他們也為寶藏而來，你要如何逃出這個島？請你根據這一情境，設計數學問題.

設計意圖：由學生完成小結中框架圖的完善工作，使學科知識更加結構化. 學生根據情境自己嘗試探索，提高提出問題能力，培養發散思維.

實際上，數學建模過程主要包括：在實際情境中從數學的視角發現問題、提出問題，分析問題、建立模型，確定參數、計算求解，檢驗結果、改進模型，最終解決實際問題. 在數學教學中，完整的數學建模可能較為費時，難以在一節課中實施. 但是，這并不影響教師在日常教學中滲透數學建模思想. 本節“解三角形的應用”的教學創新在于并不是通過獨立的、割裂的、沒有聯系的多種習題講解如何應用解三角形的知識解決實際問題，而是通過創設一個較為連貫的、有趣的、有具體情境的探險故事，串聯解三角形的多種模型，實現數學建模過程的微小化.