脈沖射流對環量控制翼型氣動性能的影響

雷玉昌，張登成，張艷華，蘇光旭

（1.空軍工程大學 研究生院，西安 710051； 2.空軍工程大學 航空工程學院，西安 710038）

飛行器上的襟翼、副翼等活動舵面一般被用來改變機翼的彎度和周圍的流場特性，進而改變機翼上的氣動力和力矩。活動舵面對提高飛行器的升力、改善升阻比起到了重要作用，但是復雜的舵面機械系統導致飛行器結構復雜、質量增加，隱身性能變差。為解決復雜的高升力舵面機械系統存在的弊端，國內外陸續使用環量控制技術來解決這個矛盾［1］。環量控制技術的發展是備受關注的主動流動控制方式之一。這種流動控制是指在機翼鈍后緣表面開縫，在后緣上噴射切向射流，利用Coanda效應（壓力與離心力的平衡使射流沿著后緣曲面流動），射流與外流混合后繞曲面外形流動，使流線偏折，并增大繞流速度，增加氣流繞翼型的環量。由庫塔儒科夫升力定理可知翼型升力會增加［2-3］。風洞試驗和數值仿真的結果表明，環量控制技術對圓形Coanda后緣穩定切向吹氣具有明顯的氣動效益，對縮短飛行器的起飛著陸距離、提高機動性等提供了可能性［3-4］。盡管有諸多好處，但是這項技術并沒有應用于實際飛行器上，因為后緣射流需要從發動機引氣或設置額外供氣裝置，由此帶來的發動機推力損失及經濟效益制約了該技術的實際應用。而脈沖射流能夠大幅度降低環量控制射流所需的質量流量，并減少引氣量［5］。考慮到節省1%的商用噴氣燃料就相當于節省100萬美元的運營成本，脈沖射流能夠帶來可觀的經濟效益［6］。為此，脈沖射流對環量控制翼型氣動性能的影響規律，在著重分析其大迎角下的實際應用價值中有重要的研究價值。

國內外對環量控制射流都進行了一定程度的研究。Yaros等［7］證明了環量控制可使機翼最大升力系數增大4倍。Jones等［8］也證明了采用環量控制的機翼可以獲得與傳統高升力系統相當甚至更高的升力，但隨著升力增大，所需要的射流質量流量也迅速增大。Kanistras等［9］通過實驗的方法研究了不同后緣曲率對氣動特性的影響，結果表明后緣曲率對升力系數的影響較大，對阻力系數的影響并不明顯。Jones等［10］提出了升力增長存在分離區和超環量控制區2個控制階段，這取決于后緣形狀和射流特性。AVT-239任務組［11］設計制作了利用環量控制技術替代傳統舵面的無人飛行器，驗證了該技術可用于改善升阻特性。朱自強和吳宗成［12］總結了之前環量控制技術研究的最新進展，并指出了國內對環量控制技術研究經驗和成果的缺乏。張艷華等［13-14］研究了環量控制的作用機理，特別是對等離子體環量控制進行了深入研究，相較于普通射流環量的控制效費比較大。南京航空航天大學、西北工業大學等也進行了相關研究［15-17］。上述研究都集中指出了定常射流只能在較低迎角下帶來巨大的升力效益，高動量系數導致失速迎角提前，并在大迎角下氣動效益變差；同時，高動量系數需要消耗大量的質量流量，影響飛行器的推力效益。這些問題都嚴重制約了環量控制技術的進一步應用。

Jones和Englar［3，18］用 脈 沖 射 流 替 代 定 常 射流用以環量控制吹氣，證明了脈沖射流能夠在取得與定常射流相當的升力情況下，降低約50%的質量流量，初步證明了脈沖射流的部分優越性，但是并未解釋射流作用機理，也未解決脈沖射流帶來的氣動力脈動問題。隨后，Shah等［5］進一步分析了脈沖射流對后緣不同位置的速度影響，以及后緣射流分離點和邊界層厚度的變化。王萬波和Warsop等［19-20］也進行了相關研究，分析了0°迎角下不同頻率時脈沖吹氣對翼型氣動性能的影響，同時指出仍需進行動量系數、占空比等因素的影響研究。已有的研究多關注脈沖射流作用下的時均氣動力效應，對相應的氣動力脈動現象和大迎角下的流動情況研究較少，難以指導實際應用。

為此，本文采用雷諾平均Navier-Stokes方法對二維環量控制翼型流場進行非定常數值模擬。對比研究脈沖射流和定常射流參數對翼型氣動特性的影響，對大迎角下的流動情況進行分析，探究減弱氣動力脈動現象的方法，為脈沖射流的具體應用提供一定的參考。

1 數值計算方法與驗證

1.1 計算模型和網格

超臨界翼型有鈍前緣、大厚弦比的特點，最大升力系數較大，內部能夠容納環量控制技術所需要的供氣機構或管道等，可以更充分地發揮環量控制增大升力的優勢，因而成為環量控制技術研究的良好翼型。本文采用相對厚度為17%的超臨界翼型NASA LS（1）-0417作為基準翼型。

翼型相對厚度為17%，弦長c=240 mm。采用文獻［18］中的修形方法，將距后緣25%弦長的部分修形處理，按照后緣半徑r/c=2%繪制柯恩達后緣曲面，射流口偏離中軸線15°，射流口高度h=0.001c。圖1為修形過的超臨界翼型示意圖，研究僅涉及上射流口吹氣。

圖1 翼型相關參數示意圖Fig.1 Sechematic map of airfoil shape parameters

計算區域選取翼型弦長的30倍，網格剖分采用結構網格，生成O型網格拓撲結構，邊界層內第一層的網格高度約為1×10-5m，射流口附近第一層網格高度為2×10-6m，保證第一層高度的壁面率y+均小于1，以滿足黏性底層的計算要求。網格總數約為58萬，圖2為翼型計算網格劃分情況。

圖2 翼型計算網格劃分Fig.2 Airfoil’s computational grid generation

1.2 計算方法

數值模擬方法采用二維雷諾平均Navier-Stokes方程，積分表達式為

式中：Q為流動變量矩陣；Ω為控制體；S為控制體面積；FC和FV分別為無黏性通量和黏性通量；n為控制體面的外法線向量。采用k-w SST湍流模型，該模型對有較大逆壓梯度的邊界層流動、分離預測性能較好。Swanson等［21-22］也曾指出該模型能較好地預測環量控制流動分離。借助商業軟件FLUENT進行相關計算，采用有限體積法離散控制方程，無黏性通量采用三階MUSCL格式，黏性通量采用二階迎風格式離散。遠場邊界為壓力遠場，壁面邊界采用無滑移壁面條件。

早期研究表明，方波脈沖射流比傳統的正弦脈沖射流效率更高［23］。因此，本節采用方波脈沖射流進行相關研究，其中脈沖射流在一個周期內對應的射流速度為

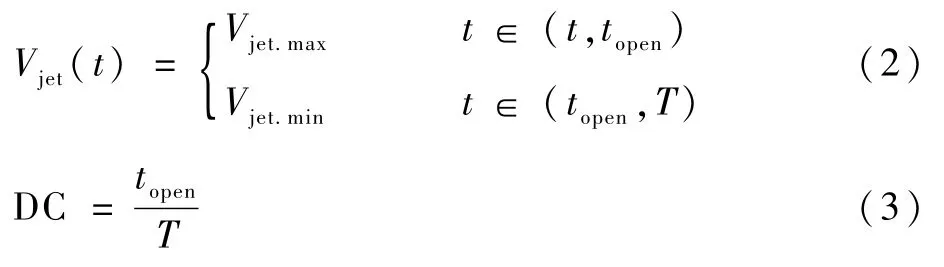
式中：T為脈沖周期；topen為一個脈沖周期中射流口產生射流的持續時間；DC為占空比；Vjet.max為在一個周期中射流產生的最大射流速度。射流動量系數為衡量射流強度、表征氣流動量的重要無量綱參數，定義為

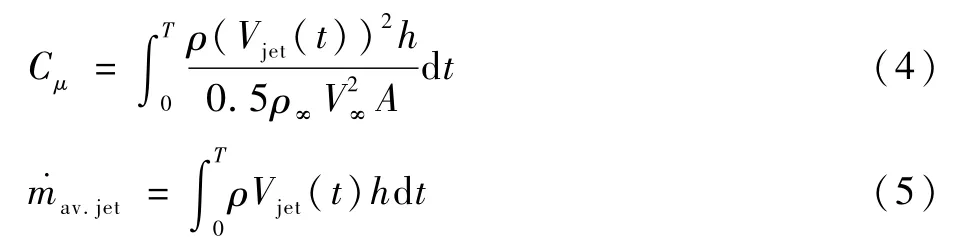
非定常計算中，物理時間步長對數值計算起著重要的作用。特別是對脈沖射流而言，出口速度隨時間變化呈現出周期性變化，時間步長必須足夠小以解析脈沖射流的周期性變化。雖然時間步長過小會嚴重影響計算效率，但是對結果沒有太大影響。圖3為不同時間步長Δt下時均升力系數CL和阻力系數CD的計算結果。當Δt≤5×10-5s時，時均升力系數CL的最大變化為0.9%，時均阻力系數CD的最大變化為2.1%，對高升力系統而言，存有一定計算誤差是可以被接受的。因此，選定計算時間步長Δt=5×10-5s，足以解析每個脈沖射流的周期性變化。

圖3 不同時間步長下的時均升阻力系數Fig.3 Time-averaged lift and drag coefficient at different time step sizes

1.3 計算方法驗證

為了驗證本文中數值計算方法的準確性，對0°迎角下不同吹氣動量系數的超臨界翼型進行了數值模擬。計算條件為：來流速度為30 m/s，來流溫度為293.15 K，雷諾數為5×105，后續研究均采用此外流條件。設置動量系數在0～0.06之間變化，將仿真結果與文獻［18］中的實驗數據進行對比，仿真采用穩態方法，結果如圖4所示，仿真結果與實驗數據基本吻合。

圖4 升力系數仿真與實驗對比Fig.4 Comparison of lift coefficient between simulation and experiment

已有的環量控制脈沖射流實驗中無高頻率內容，因此選擇文獻［3］中35 Hz脈沖射流頻率下不同占空比的情況進行對比。圖5給出了35 Hz脈沖射流頻率下的時均壓力系數Cp分布。從圖中可知，數值模擬得到的翼型上下表面的時均壓力系數Cp與實驗結果基本吻合。

圖5 35 Hz脈沖射流下時均壓力系數分布Fig.5 Time-averaged pressure coefficient distribution under 35 Hz pulsed jet

2 結果分析

2.1 占空比的影響

占空比是脈沖射流對翼型氣動特性的重要影響參數，通過調節占空比，可以獲得相應質量流量的變化。為了研究占空比對氣動特性的影響，本節對35 Hz脈沖射流頻率下不同占空比情況的翼型氣動參數進行了數值模擬。

圖6為脈沖射流和定常射流下的時均升力系數隨質量流量變化的對比曲線。其中，脈沖射流曲線對應的質量流量是在定常射流動量系數下通過改變占空比實現的；定常射流動量系數Cμ=0.02，不同占空比DC對應的射流速度如表1所示。定常射流曲線對應的質量流量是通過改變射流速度實現的，動量系數Cμ從0變化至0.02。

圖6 不同質量流量下的時均升力系數對比Fig.6 Comparison of lift coefficient at different mass flow rates

表1 不同占空比對應的射流速度Table 1 Jet velocity corresponding to different duty cycle

由圖6可以看出，在產生相同時均升力系數的基礎上，脈沖射流能夠大幅度降低射流所需要的質量流量。在占空比變化階段，脈沖射流作用下的氣動性能差別較大，較低占空比作用下，脈沖射流降低質量流量的優勢更加明顯。在給定時均升力系數為1的情況下，脈沖射流對應的質量流量減少了68.4%，同時，在占空比為40%、質量流量相等的情況下，脈沖射流對應的時均升力系數相較定常射流提高了65.3%。隨著占空比的增加，脈沖射流下的質量流量效益逐漸降低。

圖7為不同占空比作用下的時均升力系數時域變化曲線。定義Δh為升力系數周期性變化過程中2個峰值之間的差值，即升力系數脈動幅值。占空比DC越小，升力系數脈動幅值Δh越大，這是因為低占空比對應的射流速度較大，是一種持續時間短、射流動量大的穿透狀態，能在短時間內在后緣移動較大距離，而射流一旦消失，升力系數出現斷崖式下降的現象，射流消失后的升力響應速度要遠大于射流產生后的響應速度，同時，由于占空比較低，射流消失后逐漸逼近無射流狀態下的升力系數。

圖7 35 Hz脈沖射流下時均升力系數時域曲線對比Fig.7 Comparison of lift coefficient time-domain curves at 35 Hz pulsed jet

綜上所述，在產生相同時均升力系數的前提下，脈沖射流需要的質量流量更小，且占空比越小，這種優勢越明顯。但是，低占空比下導致的射流穿透效應將會直接導致升力系數脈動幅值增大。當DC=30%時，Δh可達1.3，這在實際飛行中將會導致劇烈的抖振現象，嚴重影響飛行安全，在實際應用中是不可取的。因此，實際應用中應當選用較高占空比的脈沖射流，選取DC=70%進行后續研究，并進一步探索脈沖射流的實際應用前景及降低Δh的方法。

2.2 頻率的影響

圖8給出了在不同迎角α下頻率的改變對升力系數增量ΔCL的影響。低迎角（0°）下，隨頻率增加，升力系數增量呈現先增加后降低的趨勢，但整體變化幅度不大，在高頻率（200 Hz）下，脈沖射流甚至低于定常射流作用下的升力系數增量；高迎角（15°）下，隨頻率增加，升力系數增量呈現持續增加的趨勢，在高頻率（200 Hz）下，脈沖射流遠遠高于定常射流作用下的升力系數增量。在不同迎角下，隨頻率增加，脈沖幅值Δh均逐漸減小，約在100 Hz逐漸穩定。綜上所述，高頻脈沖射流在較大迎角下有突出的應用優勢，具備替代定常射流進行流動控制的潛力。

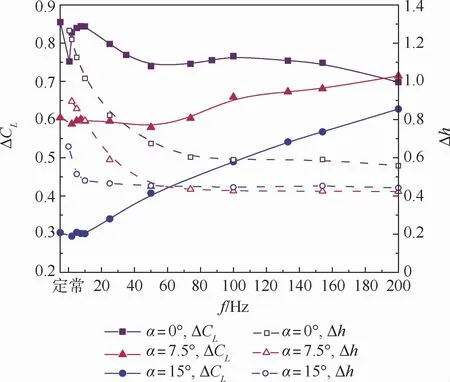
圖8 不同頻率下的升力系數增量和脈動幅值對比Fig.8 Comparison of lift coefficient and pulsation amplitude at different frequencies

為了分析脈沖射流作用下的流場作用機理，圖9給出了迎角分別為0°和15°時200 Hz脈沖射流與對應定常射流作用下的翼型整體渦量圖和后緣局部流線放大圖。其中脈沖射流作用下各時刻對應的時均升力系數如圖10所示，低頻率下射流消失后時均升力系數不再呈現出斷崖式下降的現象。

圖9 翼型渦量圖和流線圖Fig.9 Airfoil vorticity and streamlines

以15°迎角為例進行分析，從定常射流作用下的翼型流線圖中可以看出，翼型上表面已經出現大規模分離流動，渦流區較大，繼續增大迎角會導致升力下降和阻力增加，翼型進入失速分離階段。而脈沖射流作用下的翼型上表面分離渦與尾渦在一個脈沖周期內逐漸相互耦合，共同向后移動形成尾跡，上表面分離點明顯后移，渦流區明顯小于定常射流。而0°迎角下的翼型流線圖，定常射流作用下的流動始終附體，并未出現分離流動，脈沖射流作用下的上表面渦量分布與定常射流作用下的渦量分布差別也并不明顯。

從脈沖射流作用下的翼型流線圖中可以看出，在T/6時刻，翼型上表面存在分離流動，并存在一個順時針的分離渦，由于后緣射流的產生，后緣上方存在一個逆時針尾渦，同時，后緣射流下存在一組較小的附著渦，翼型處于臨界失速狀態。當進入2T/6時刻，隨著后緣持續射流，后緣壓力逐漸減小，后緣上方的逆時針尾渦先向后移動，此時上表面分離渦變化不大。當進入3T/6時刻，后緣壓力繼續減小，此時翼型上表面的分離渦也逐漸后移，分離渦幾乎已經移動至翼型尾端，翼型已經遠離失速狀態，后緣渦進一步后移會導致升力系數下降，如圖10中2T/4時刻所示。

圖10 200 Hz脈沖射流下時均升力系數時域曲線對比Fig.10 Comparison of lift coefficient time-domain curves at 200 Hz pulsed jet

當進入4T/6時刻，原尾渦向后移動至消散，上表面分離渦逐漸呈現脫離狀態，逐漸耦合形成新的尾渦。當進入5T/6時刻，射流已消失，此時分離渦已完全脫離，與原本位于射流下方的附著渦相互耦合，向后移動。尾渦逐漸被外流吹散，上表面流動逐漸恢復為附體。此時由于射流存在時滯效應，后緣壓力并未迅速提高。當進入6T/6時刻，后緣無射流，此時流動狀態趨向于15°迎角下的無射流定常狀態，鈍后緣形成新的一組附著渦，翼型上表面壓力較低，附著渦逐漸上移形成上表面的大分離區。隨后，后緣射流產生，射流上方產生新的尾渦，下方產生新的附著渦，流動開始向下一個周期發展。

總體來看，翼型上表面的分離渦和后緣尾渦在一個周期的演化過程中，經歷了形成、后移、脫落、消失、再形成的過程。而高頻脈沖射流在大迎角下的氣動效益如此突出，是因為其不斷促進翼型上表面的分離渦脫落。

與15°迎角相比，0°迎角定常射流作用的翼型上表面并未分離，流動始終附體。從整體流場來看，15°迎角上表面的分離渦不斷被吹除，渦流區明顯減小，較定常射流而言，升力增大；而0°迎角上表面不存在分離渦，尾跡受射流速度的影響跨度明顯較長，較定常射流而言升力略有降低。

從后緣流場來看，在整個周期并未形成如同15°迎角下明顯的分離渦與尾渦相互耦合向后移動的狀態，更多表現為流線的上下偏折。這是因為0°迎角上表面渦強較弱，后緣難以耦合形成有效的渦旋。0°迎角下被不斷吹除的尾渦強度較低，連續性也較弱，因此，0°迎角下脈沖射流受頻率影響較低。

因此，對于低迎角而言，脈沖頻率更多表現為對升力系數的直接影響，與定常射流的作用機理是一致的，其效果類似于間歇性施加射流；而對于高迎角而言，脈沖頻率更多與分離渦移動、尾緣渦脫落頻率等相關，這種流動狀態已經與定常射流完全不同。特別是在整個流動周期中，分離渦的移動都遠離失速狀態，這一特性表明借助脈沖射流有望突破靜態失速迎角這一禁區。

2.3 動量系數的影響

圖11為不同動量系數下脈沖射流、定常射流、無射流及基準翼型NASA LS（1）-0417的升力系數對比曲線。基于上述對占空比的研究，選取脈沖射流占空比為70%，動量系數分別為0.02和0.04。從圖11（a）可以看出，在動量系數為0.02的情況下，當迎角小于10°時，定常射流能夠較大幅度地提高翼型升力系數，當迎角大于10°時，提升幅度逐漸降低，而且失速迎角提前。為了衡量動量系數帶來的影響，引用效費比ΔCL/Cμ參數。0°迎角下，翼型效費比為42.6，此時翼型升力系數提高144.5%；而15°迎角下，翼型效費比降為15.2，此時翼型升力系數僅提高18.8%，同時，失速迎角由15°提前到10°。當迎角小于5°時，定常射流升力系數大于脈沖射流；當迎角大于5°時，定常射流升力系數小于脈沖射流。相較定常射流，脈沖射流能在更大的迎角范圍內大幅度提高翼型升力系數，更加適合在大迎角下工作。在15°迎角時，ΔCL/Cμ=38.3，此時翼型升力系數仍能提高46.3%，同時，失速迎角大幅度延遲。

圖11 升力系數對比Fig.11 Comparison of lift coefficient

從圖11（b）可以看出，提高動量系數至0.04后，對于定常射流而言，在0°迎角下，ΔCL/Cμ=36.9，而在15°迎角下，翼型效費比降為11.9。隨著動量系數的增加，定常射流的升力效益降低。定常射流對應的失速迎角也進一步提前，由15°提前至7.5°，同時，脈沖射流升力系數大于定常射流的轉折迎角提前至2.5°。此時相較定常射流，脈沖射流在大迎角下有更突出的升力表現，在15°迎角下，ΔCL/Cμ=36.7。隨著動量系數的增加，定常射流下的失速迎角會進一步提前，嚴重制約定常射流的升力效益。而脈沖射流大大擴寬了飛行器的可用迎角，甚至超過了無射流狀態下的失速迎角，隨動量系數增大，這種優勢變得更加突出，完全彌補了定常射流在大迎角下存在的缺陷和不足。

從無射流狀態和基準翼型NASA LS（1）-0417的升力系數對比中可以看出，修形后的環量控制翼型在無射流狀態下升力系數比NASA LS（1）-0417高，添加射流后升力系數進一步提高。

為了更加全面地衡量脈沖射流、定常射流、無射流和基準翼型4種狀態下的氣動效益，并合理考量射流產生所需的能量消耗，參考文獻［24］，假設射流是通過安裝在機翼內部的氣壓泵實現的，氣壓泵吸入外界自由流動的氣體后，經過壓縮送入噴射槽形成射流。因此，能量消耗功率可由質量流量和總焓變化表示：

式中：Pc，jet為射流產生的能量消耗功率系數；Pt2和Tt2分別為自由來流的總壓和總溫；Pt1為射流出口處的總壓；η為氣壓泵的工作效率，本節取0.85。脈沖射流采用振蕩吹氣執行器，即通過交替打開和關閉氣壓泵與噴射槽之間的連接，或打開和關閉氣壓泵與流體吸入通道之間的連接，通過調節閥門開度能夠實現穩定或振蕩射流。

為綜合分析氣動特性和能量消耗特性對射流控制效果的影響，采用Seifert［6］提出的氣動品質因子AFM1進行衡量。該指標以升阻比為衡量基準，將射流功率轉換為等效阻力，該值越大，則表明為執行器提供功率比為動力裝置提供功率更有效，在增升減阻方面更有利，并表征射流控制效率越高。氣動品質因子AFM1定義為

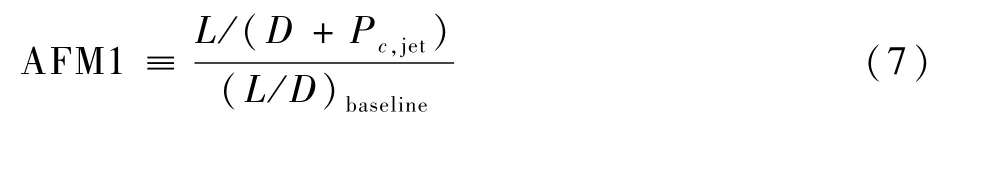
式中：（L/D）baseline為環量控制翼型無射流狀態下的升阻比。

圖12為不同情況下的AFM1對比曲線。環量控制翼型較基準翼型NASA LS（1）-0417而言，升阻比較低，這表明修形后的環量控制翼型盡管升力系數較大，但對應的阻力系數增長更為明顯，導致升阻比降低，特別是在大迎角下降低明顯。

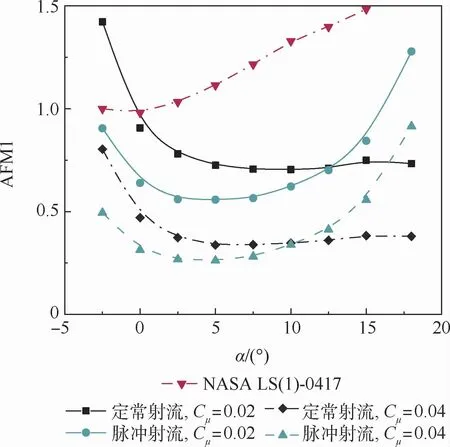
圖12 氣動品質因子對比曲線Fig.12 Aerodynamic quality factor comparison

對定常射流而言，隨迎角增大，控制效率逐漸降低，然后基本保持不變。對脈沖射流而言，隨迎角增大，控制效率先降低，然后迅速提高，逐漸超越定常射流。這是因為在中低迎角下，定常射流提升升力作用明顯，而耗能低于脈沖射流，控制效率較高；隨迎角增大，定常射流對升力的影響逐漸減弱，同時，翼型提前進入失速狀態，控制效率降低。而脈沖射流在大迎角下升力系數提升明顯，失速迎角推遲，控制效率逐漸增高。在考慮了射流消耗的情況下，脈沖射流仍能夠部分改善環量控制翼型在大迎角下的氣動效益，這與上文的研究是一致的。

2.4 疊加效應的影響

上述研究已經證明了脈沖射流在大迎角下卓越的性能優勢，解決了定常射流在高動量系數、大迎角下升力增益較差的問題。但是由脈沖射流所帶來的升力系數脈動現象仍未完全解決，本節提出采用脈沖射流與定常射流相疊加的方式來降低脈沖射流的升力脈動現象。維持其他參數不變，其中脈沖射流頻率為200 Hz，DC=70%，Cμ=0.04。

定義定常射流部分與脈沖射流部分的比例為占比rsp，即rsp=Vjet.min/Vjet.max。疊加效應即研究占比rsp對氣動特性的影響。圖13為在15°迎角下，定常射流部分與脈沖射流部分不同占比rsp對應下的時均升力系數和脈動幅值變化趨勢。隨rsp的增加，時均升力系數逐漸下降，并且呈現先慢后快的下降速度。這表明適當添加定常射流并不會大幅度降低時均升力系數，同時能夠有效降低單一脈沖射流時的升力系數脈動幅值。當rsp為0.84時，時均升力系數僅降低約12%，升力系數脈動幅值降低約80%，此時升力系數脈動幅值約占時均升力系數的3.7%，已經遠遠低于正常狀態下大迎角下升力系數的脈動幅值［25］，能夠滿足飛行器在大迎角下的氣動力要求。當rsp約為0.8時，有效解決了脈沖射流帶來的氣動力脈動問題，擴寬了環量控制技術的可用迎角范圍。

圖13 不同r sp下的時均升力系數與脈動幅值對比曲線Fig.13 Comparison of lift coefficient and pulsation amplitude at different rsp

圖14給出了rsp分別為0.566和0.84時的后緣流線變化圖。從整體上來看，后緣流場中的脫體渦都經歷了生成、后移、脫落的過程。當rsp=0.566時，定常射流占比較低，定常射流速度較小，無法突破后緣外側流動到后緣下方，當產生高速的脈沖射流后，射流需要從翼型后緣上方移動到后緣下方，導致升力系數脈動程度劇烈；當rsp=0.84時，從整體上來看，后緣流場中的脫體渦移動并不明顯，此時定常射流占比較高，定常射流速度較大，已經突破后緣外側流動到了后緣下方，此時在整個射流階段，射流一直在翼型后緣下方進行移動，升力系數脈動減弱，同時，能夠較大程度地保留脈沖射流不斷促進翼型上表面的分離渦脫落特性，因此升力系數的下降并不明顯。

3 結 論

本文采用非定常數值模擬方法，對脈沖射流作用下的環量控制翼型進行了相應研究，特別是分析了脈沖射流的實際應用前景，得到以下結論：

1）維持動量系數不變的情況下，較定常射流而言，占空比越低，脈沖射流減小質量流量的優勢越明顯，但同時升力系數脈動的劣勢也越明顯。

2）在占空比不變的情況下，小迎角下升力系數隨脈沖頻率增加而呈現先增加后降低的趨勢，但整體變化幅度不大；大迎角下升力系數隨脈沖頻率增加而持續增加，高頻脈沖射流在大迎角下有突出的應用優勢。

3）脈沖射流作用下，翼型上表面的分離渦和后緣尾渦通過形成、后移、脫落、消失、再形成的過程，延遲了翼型失速，改善了翼型在大迎角下的氣動特性，并且隨動量系數的增大，這種優勢更加明顯。

4）采用脈沖射流和定常射流相疊加的方式能有效減弱升力系數脈動幅值過大的問題，當rsp約為0.8時，能有效擴寬環量控制技術的使用迎角。