一種基座姿態可控空間機器人的通用避奇異算法

趙龍澤，佘浩平，*，黃良偉，黃龍飛

（1.北京理工大學 宇航學院，北京 100081； 2.中國空間技術研究院 錢學森空間技術實驗室，北京 100094）

對于基座姿態可控的關節型空間機器人，在對其進行笛卡兒空間連續運動規劃的過程中，需要利用基于雅可比矩陣求逆或偽逆的速度級運動學求解來實現。然而，當機器人經過一些特定的臂型時，不可避免地會遇到運動學奇異，主要是因為雅可比矩陣出現了病態，此時如果繼續采用經典的速度級逆運動學求解方法，則在機械臂的奇異點附近會導致規劃關節角速度和角加速度出現無窮大的極端情況，機械臂會因此出現振動，影響機械臂的軌跡跟蹤精度，同時也不利于機械臂的關節運動控制，甚至造成控制算法失效［1］。因此，尋求一種有效的回避算法是極為重要的。

早期常采用偽逆法進行機械臂奇異回避的路徑規劃，該方法雖然能夠解決一些超定或欠定的問題，但關節角的解仍會在機械臂的奇異區內出現跳變，造成較大誤差［2］。隨后Nakamura等［3］和Wampler［4］分別提出了阻尼最小方差法（DLS）和奇異性魯棒逆解（SRI）的方法。Chiaverini［5］對SRI方法進行了改進，采用“阻尼最小方差+數值濾波”的方法，通過判定最小奇異值施加阻尼系數，提升了規劃精度。SRI方法雖然能夠有效保障機械臂在奇異區內關節角度的連續性和有限性，但仍存在機械臂末端跟蹤精度較差的問題，且由于需要對雅可比矩陣進行實時的SVD分解，運算量也較大。楊震等［6］引入雅可比矩陣的條件數作為DLS法中選取阻尼系數的衡量指標，有效提高了求解精度，但由于其需要頻繁地對雅可比矩陣進行奇異值分解，極大地提高了計算量。董伯麟和彭航［7］給出了雅可比矩陣條件數的一個更小的上界估計式，提高了運算速度，但犧牲了一定的位姿精度。

Cheng等［8］以PUMA型機械臂為研究對象，提出了“奇異分離+緊密二次型規劃”（SCIQP）法，避免了對雅可比矩陣進行實時SVD分解，有效減少了算法的運算量。徐文福等［9］針對PUMA型機器人的特點，對奇異分離的算法進行了改進，提出了“奇異分離+阻尼倒數”的方法，采用阻尼倒數代替普通倒數，僅犧牲末端部分方向的精度，以較小的運算量完成了奇異回避。崔洪新等［10］采用指數級阻尼倒數代替普通阻尼倒數的方法，進一步減小了跟蹤誤差。劉成良等［11］采用協調控制的算法回避了機器人的腕部奇異。Choi等［12］引入高斯分布阻尼因子，進一步提高了機械臂在奇異點附近的算法穩定性，但該算法本身就存在一定的不連續性。吳戈等［13］對高斯分布阻尼因子進行了改進，減小了跟蹤誤差，但魯棒性并不高。Qiu等［14］通過引入與最小奇異值相關的修正向量，從而控制規劃角速度，其性能僅受最小奇異值下限選擇的影響，但損失了一定的實時性。Nanos和Papadopoulos［15-16］從 初 始 機 械 臂 的 關 節角和基座位姿出發，通過合理設置初值的方法避免了雅可比矩陣的奇異，但該方法未考慮基座受到擾動的情況。

本文針對不同自由度的基座姿態可控空間機械臂，在進行一般建模后，通過建立雅可比矩陣，進行速度級運動學逆解分析，在進行路徑規劃的同時判斷雅可比矩陣行列式的值，給出奇異判定條件，從而判定機械臂的奇異區。隨后，在奇異區內提取各關節角的微分項，通過設計二次擬合方法在奇異區內對關節角進行分段規劃，最終實現了一種通用性較強的奇異回避算法。

1 運動學模型分析

1.1 基座姿態可控空間機械臂的建模

在慣性坐標系下建立空間機械臂的一般模型，如圖1所示。空間機械臂由n個僅有一個自由度的旋轉關節和n+1個剛體桿件串聯而成，其中航天器平臺記為機械臂的基座，記為連桿0，連桿i為空間機械臂所對應的第i個桿件，關節i為連接第i-1個連桿與第i個連桿的關節。為方便問題分析，可對模型做出以下幾點假設：①可以同時對基座姿態及各關節力矩進行控制，實時保證基座姿態可控；②忽略模型的柔性，將模型的所有部分都視為剛體；③忽略各項外力的影響［17］。

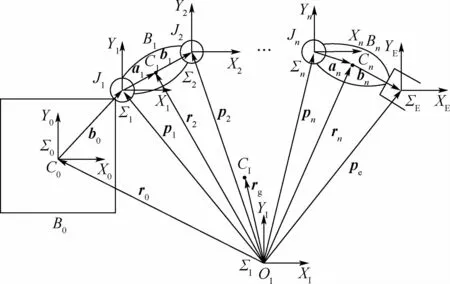
圖1 空間機械臂的一般模型Fig.1 General model of a space manipulator

圖1中的符號說明如下：B0為空間機器人的基座；Bi（i=1，2，…，n）為機械臂的第i個連桿；Ji（i=1，2，…，n）為機械臂的第i個關節；Ci（i=0，1，2，…，n）為第i個連桿的質心；OI為慣性坐標系的原點；ΣI為慣性坐標系；ΣE為機械臂末端執行器所固連的坐標系；Σi（i=0，1，2，…，n）為與連桿i固連的坐標系，本文采用剛體固連坐標系的建立原則；ki（i=1，2，…，n）為Ji旋轉方向的單位矢量；rg為空間機械臂系統質心在慣性坐標系中的位置矢量；ri（i=1，2，…，n）為Bi的質心位置矢量；pi（i=0，1，2，…，n）為關節i的位置矢量；pe為機械臂末端位置矢量；θi（i=1，2，…，n）為關節i的關節角；Θ為由θi到θn依次排列組成的關節角向量；b0為Σ1的原點在Σ0坐標系中的位置矢量；ai和bi（i=1，2，…，n）分別為從關節i指向連桿i質心的位置矢量和從連桿i質心指向關節i+1的位置矢量。

定義叉乘操作數：若s=［x y z］T，則

由式（1）可得，矢量叉乘運算表示為

各連桿質心的線速度vi可表示為

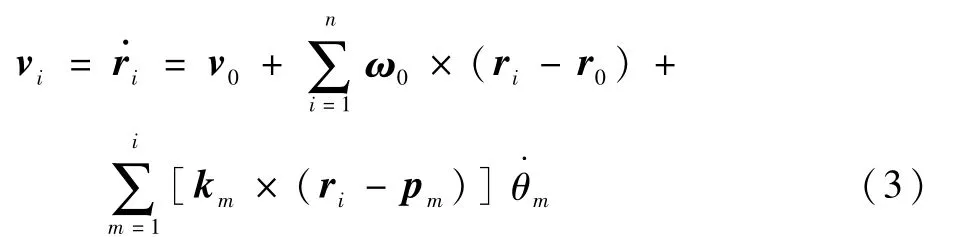
式中：v0、ω0分別為基座線速度、角速度。

機械臂的末端線速度ve可表示為

末端角速度ωe可表示為

將式（4）與式（5）聯立，可得

式中：Jb、Jm分別為基座運動雅可比矩陣、機械臂運動雅可比矩陣。

由于空間機械臂系統滿足線動量守恒，則有

式中：P為系統的線動量；mi（i=0，1，2，…，n）為剛體i的質量。

將式（3）代入式（7）并整理，可得

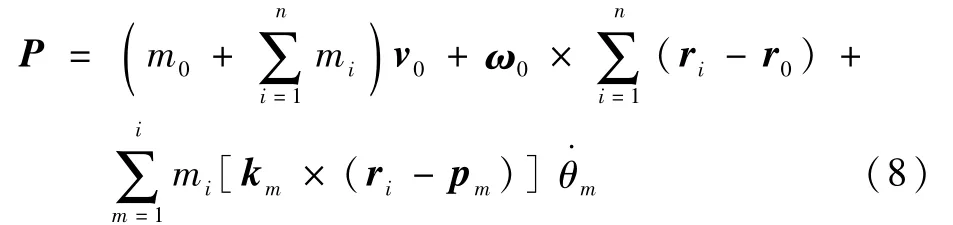
系統總質量為

式中：M為系統總質量。

由假設③可知，系統不受任何外力，故系統的質心為

將式（8）代入式（7），可得

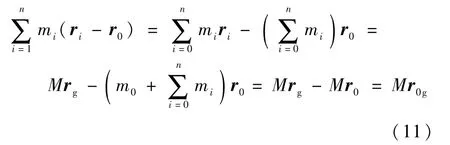
將式（9）和式（11）代入式（8），可得系統的線動量守恒方程為

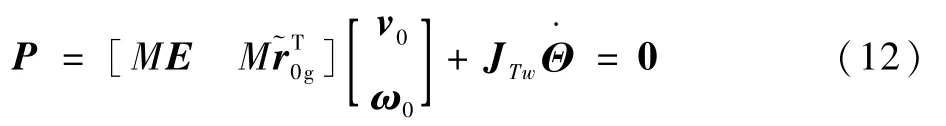
式中：

由于基座姿態是指處于受控狀態，基座角速度可近似忽略，即

將式（15）代入式（12），可得

將式（15）、式（16）代入式（6），可得

采用虛擬機械臂法［18］建立基座受控空間機器人的微分運動方程為

聯立式（17）和式（18），可得

1.2 奇異性分析

2 基于“微分項提取＋二次擬合”的奇異回避算法

2.1 總體思路

在對機械臂進行笛卡兒路徑規劃時，已經預先得到每一迭代步的末端位姿狀態向量。由第1節分析可知，在機械臂進行笛卡兒路徑跟蹤時，通過確定關節角發生跳變的臨界點，從而判定奇異區的關節角范圍，即可確定在雅可比矩陣不發生奇異的情況下其行列式所對應的閾值。

在確定奇異區的關節角范圍后，實時讀取每一迭代步已預先規劃好的末端位姿狀態向量，采用基于Newton-Raphson迭代法的機械臂逆運動學的數值解法可以得到奇異區內任意迭代步所對應的關節角［19］。隨后，采用一種“微分項提取+二次擬合”的方法，對機械臂在奇異區內的關節角序列進行擬合，最終得到完整的奇異區角度序列和角速度序列。在脫離奇異區后，保持期望末端位姿不變，以當前末端位姿矩陣為初始時刻末端位姿，重新進行笛卡兒空間內的連續位姿跟蹤，最終完成奇異回避任務。

2.2 機械臂逆運動學的數值解法

在本文所述的奇異回避算法中，需要對奇異區內已規劃好的末端位姿進行運動學求逆，得到關節角，從而為奇異區內的關節角擬合提供輸入。

對任意自由度的空間機械臂，已知機械臂當前時刻的關節角序列qr，即可得到其所對應末端位姿矩陣為

假設期望末端位姿狀態變量為

可得到末端姿態矩陣為

期望末端位置矢量為

當前時刻與終止時刻的末端位置矢量差值為

記下當前時刻的姿態矩陣 Rr=［nrorar］與終止時刻的期望姿態矩陣Rf=［nfofaf］，計算由Rr到Rf的姿態變換的歐拉軸角參數（kf，φf），由此計算當前時刻與終止時刻的末端姿態矢量差值Δe為

聯立式（26）、式（27）和式（20），得到基于速度級的逆運動學求解方程為

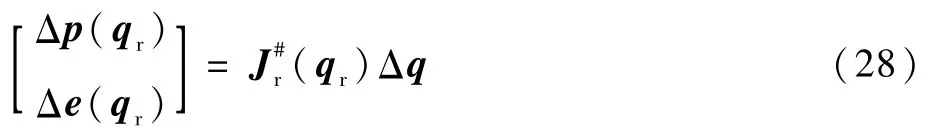
機械臂逆運動學的數值解法算法流程如圖2所示。

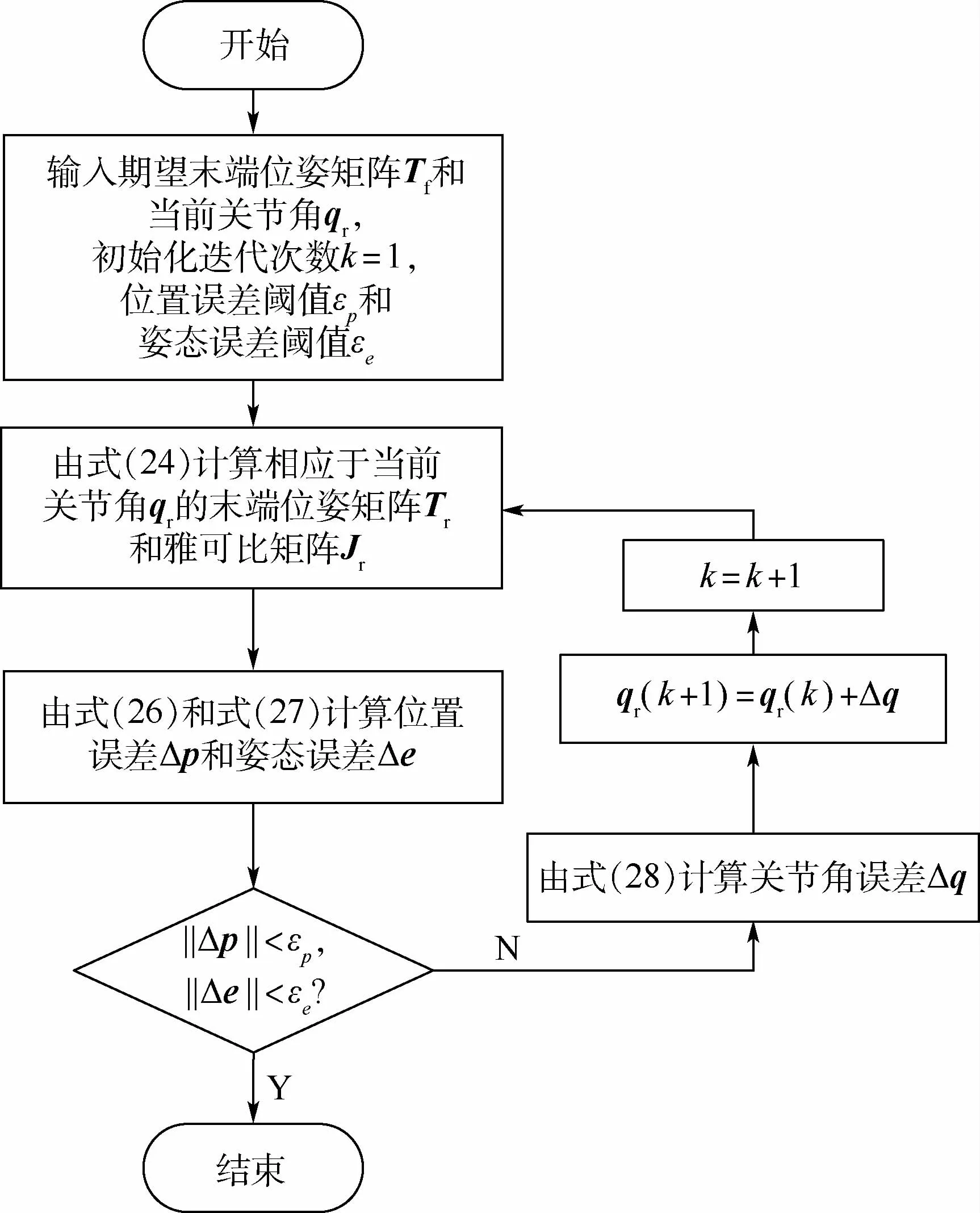
圖2 機械臂逆運動學的數值解法算法流程Fig.2 Flowchart of inverse kinematics numerical solution algorithm of manipulator

需要說明的是，對于相同的末端位姿矩陣，可能存在關節角的多解情況。本文算法所得到的關節角迭代值與給定初始值的相關程度較大，因此在使用本文算法時，應保證在關節角初值的鄰域內至少存在一組解，防止在迭代過程中出現角度突變。

2.3 奇異回避算法的實現流程

2.3.1 奇異區的判斷

需要指出，設定εΔq的值越大，奇異區越小［20］。

2.3.2 進入奇異區后的機械臂路徑規劃

步驟1 以機械臂當前關節角為輸入，進行笛卡兒空間連續位姿跟蹤，若不出現奇異，則轉步驟6，反之轉步驟2。

步驟2 判定機械臂進入奇異區后，讀取上一迭代時刻的關節角qj-1，作為2.2節所述算法的初始關節角輸入。

步驟3 初始化機械臂末端位姿矩陣誤差閾值εT，每隔k步讀取一次奇異區內所規劃的末端位姿狀態變量Xek，并記下相鄰2次讀取時間間隔Δt，作為2.2節所述算法的期望末端位姿矩陣輸入，可得到期望關節角qek。

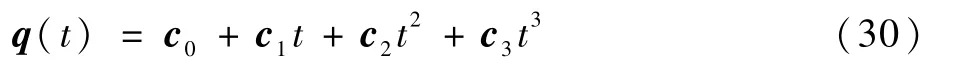
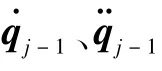
將式（31）代入式（30），可得終端時刻微分項方程組為

式（32）提取出了期望關節角的微分項，在一些特殊情況下，用式（30）所得到的關節角速度曲線會出現龍格現象［21］，同樣會造成關節角突變問題，因此需要對關節角進行二次擬合，避免此種問題的產生。

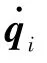
式中：ti為奇異區內第i次迭代時所對應的的仿真時間。令

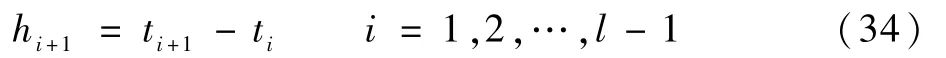
假設θ″（t）在［ti，ti+1］區間內為線性函數，則

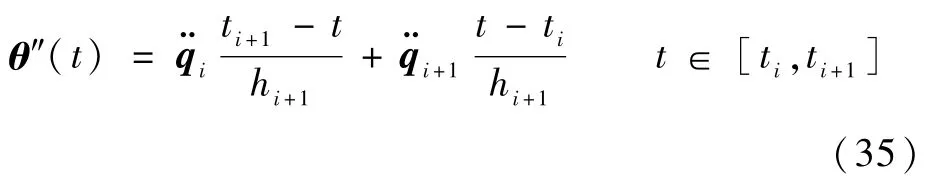
將式（35）積分2次，可得

由式（36）可得

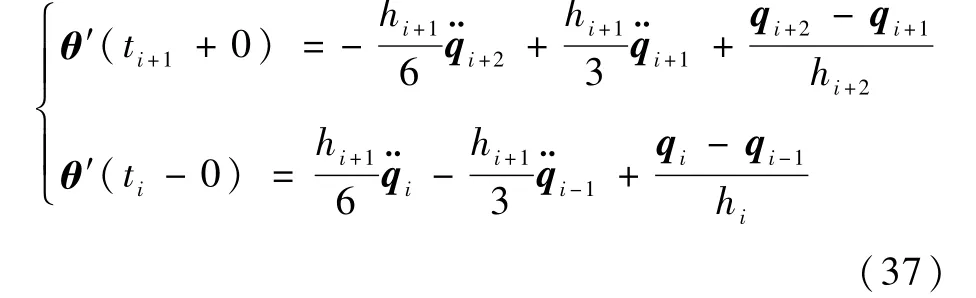
聯立式（36）和式（37），可得

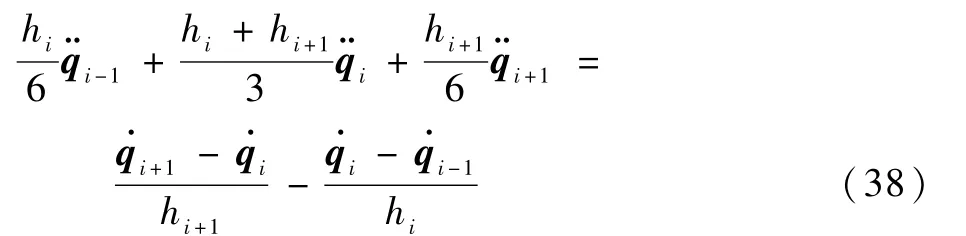
記

聯立式（36）～式（38），可得

由式（40）和式（41）整理，可得

通過求解式（36）的方程組，即可完成所有I=［ti，ti+1］，i=0，1，2，…，l-1區間內的關節角度、角速度和角加速度序列的求解。

需要指出，k的值越小，跟蹤精度越高，同時計算量也會相應增大。

步驟5 記錄機械臂在奇異區內的每一迭代步的機械臂末端位姿Td，若滿足：

則停止規劃，輸出機械臂的關節角序列。反之，規劃繼續進行，直至離開奇異區后，轉步驟1。

步驟6 記錄全部規劃過程的關節角和關節角速度序列，完成機械臂的路徑跟蹤。

經過上述6個步驟，可完成機械臂在笛卡兒連續位姿跟蹤過程中的奇異回避。空間機械臂奇異回避算法流程如圖3所示。

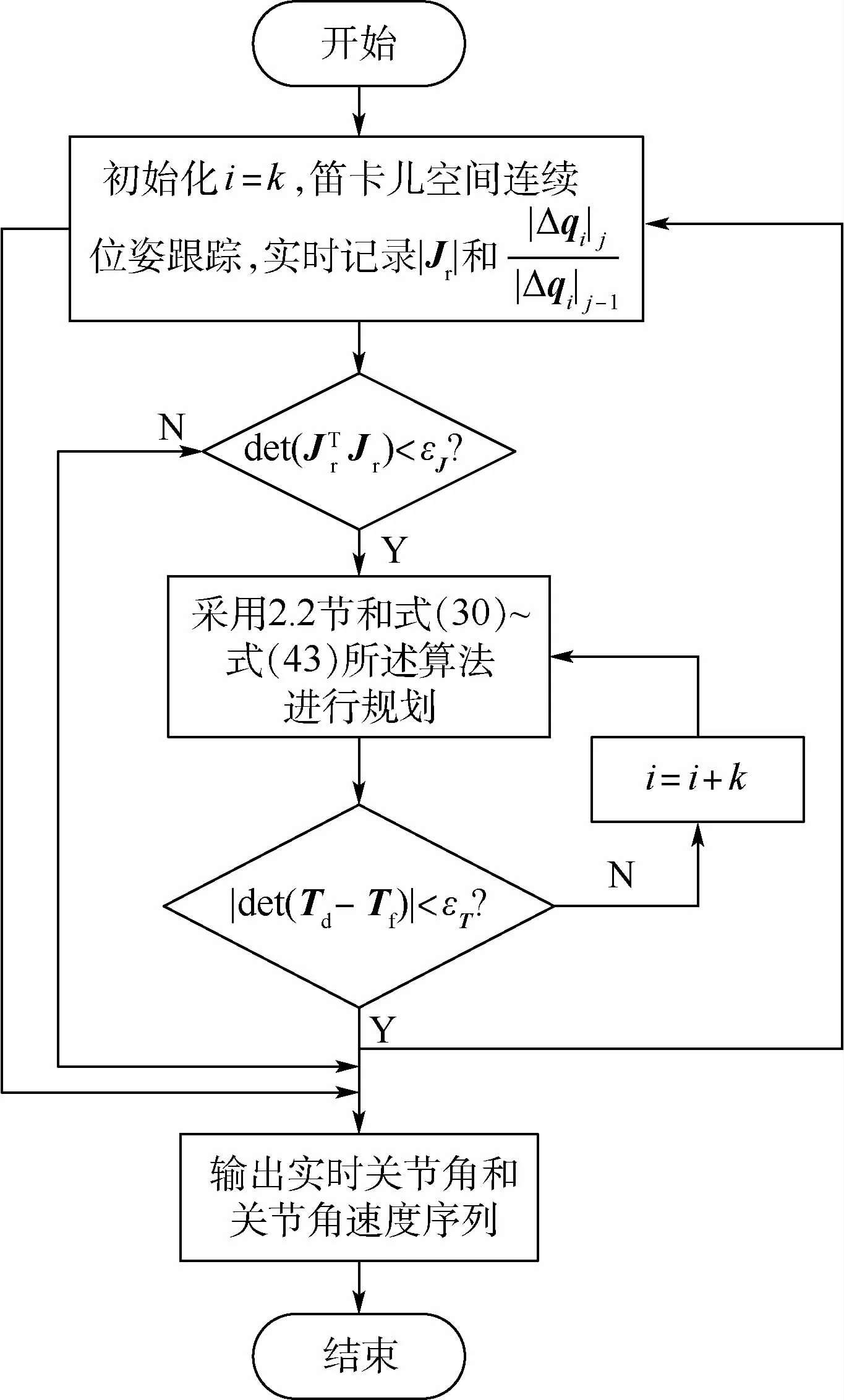
圖3 空間機械臂奇異回避算法流程Fig.3 Flow-chart of singularity avoidance algorithm for space manipulator

3 仿真驗證

3.1 機械臂模型及仿真參數設置

本文以常用的6R空間機械臂為研究對象，其系統模型如圖4所示，圖4中坐標系基于DH方法創建。

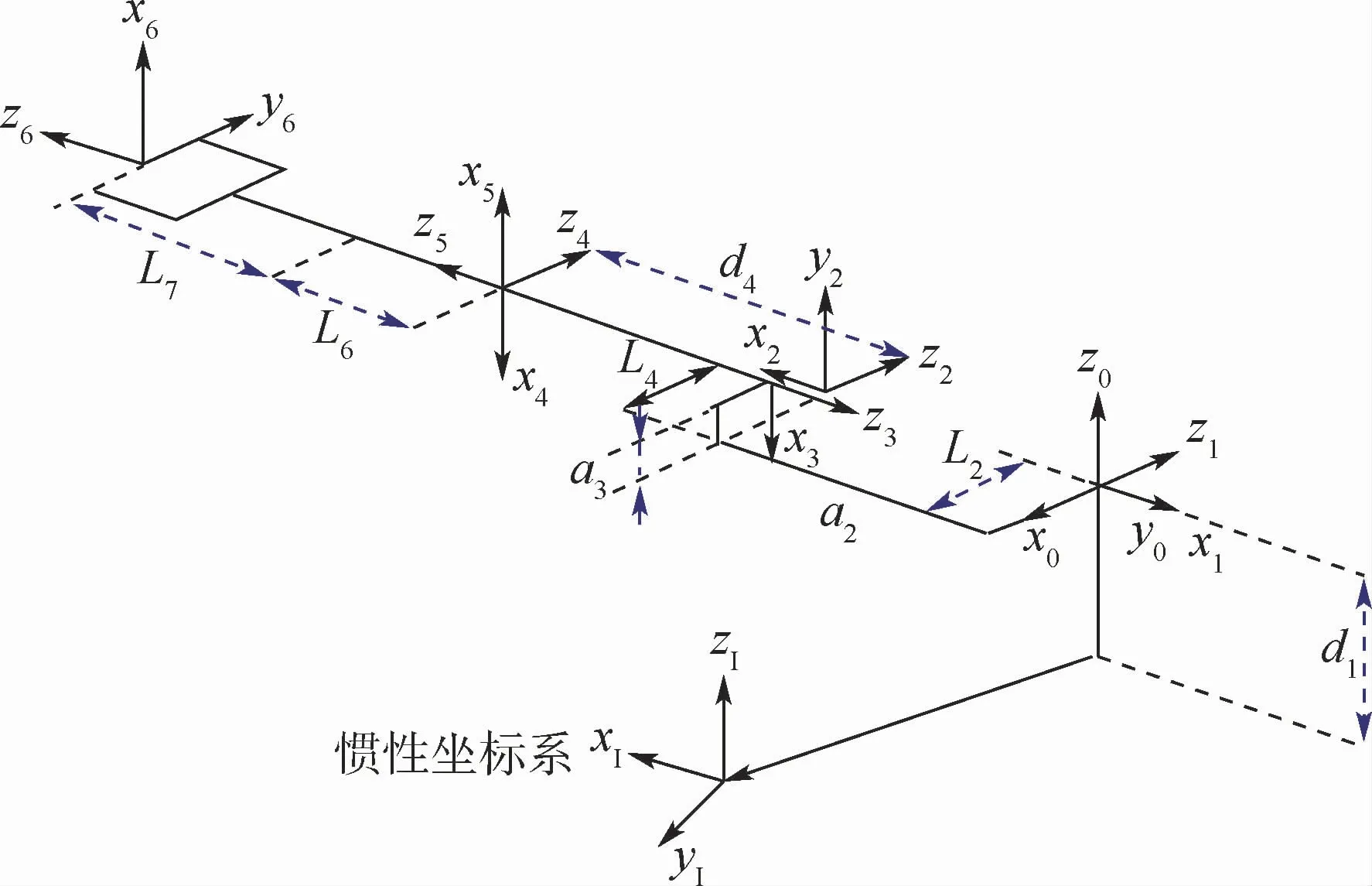
圖4 6R機械臂的結構簡圖Fig.4 Structure of 6R manipulator

文獻［19］給出了其質量特性參數，其中L1、L4、L6、L7的值分別為0.30、0.15、0.10、0.234 5 m，d1、d2、d4的值分別為0.30、0.15、0.70 m，a2、a3分別為0.83、0.03 m。

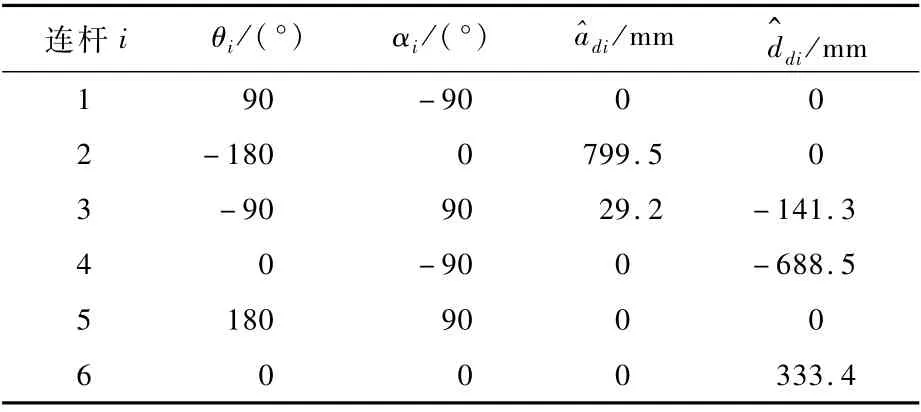
表1 6R機械臂的DH參數Table 1 DH parameters of 6R manipulator

3.2 算法校驗

本文采用直線位姿跟蹤，以梯形速度插值規劃機械臂的末端位姿，驗證本文算法的奇異回避效果。

設定基座姿態為ψb=［0，0，0］，初始時刻的系統關節角為

Θ=［47.61° 110.2° -78.07° 85.23°-30° 77.68°］

系統初始時刻的末端位姿Pe0及期望末端位姿Pef分別為

Pe0=［0.384 6 m -0.384 6 m 1.283 0 m 55.67° 61.10° -18.13°］

Pef=［0.597 7 m -0.129 3 m 1.306 5 m 51.86° 51.92° 37.49°］

式中：位姿向量的前3項為機械臂末端相對于基坐標系的位置坐標；后3項為末端姿態歐拉角，設定規劃時間為20 s，加減速時間為4 s。

采用經典笛卡兒路徑跟蹤算法，得到機械臂各關節的角速度曲線，如圖5所示。可見，在8.8 s左右，關節角速度開始出現跳變，仿真過程出現奇異。設定εΔq=5，εT=10-8，判定奇異區在8.8～11.2 s區間內。選取k=1，在采用2.3節所述的奇異回避算法進行重新規劃后，關節角速度曲線如圖6所示。

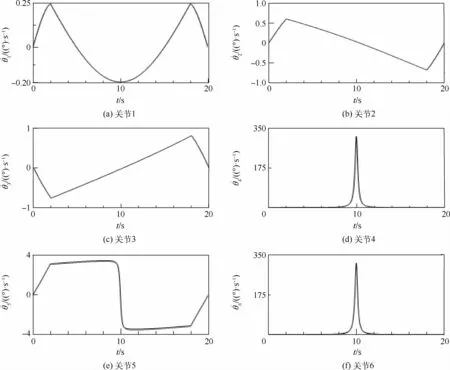
圖5 未進行奇異回避時機械臂各關節角速度Fig.5 Angular velocity of each joint of manipulator without singularity avoidance

在進入奇異區后，發生奇異的關節角速度仍會出現小幅振蕩，這是由于在進入奇異區以前，雅可比矩陣已經逐漸趨于病態，隨著迭代的進行出現誤差積累，在進入奇異區后，機械臂需要較快地調整關節角，以減小迭代誤差，完成位姿跟蹤。

由圖6可見，機械臂在經過奇異區時，關節1到關節3的角速度未受影響，關節5的角速度出現了［-5°，3°］區間內的小幅振蕩，原本發生奇異的關節4和關節6的角速度出現了在［-5°，3°］區間內的小幅振蕩，但其幅值仍然得到了明顯的控制，避免了奇異的發生。

圖6 進行奇異回避后的機械臂各關節角速度Fig.6 Angular velocity of each joint of manipulator after singularity avoidance

分別選取k=1、5、10時，代入2.3節所述算法中，得到的末端位置跟蹤誤差和末端姿態跟蹤誤差曲線分別如圖7和圖8所示。

由圖7和圖8可見，本文算法可以較好地完成連續位姿跟蹤任務。k值選取越小，機械臂在剛好進入奇異區時的跟蹤誤差越大，這同樣是由于迭代過程中已經產生誤差積累的緣故，上文已進行詳細說明。在奇異區內經過短暫規劃后，其末端位姿跟蹤精度則隨著k值的減小顯著提升。

圖7 k取不同值時末端位置誤差對比Fig.7 Comparison of terminal position errors when k is taken as different values

圖8 k取不同值時末端姿態誤差對比Fig.8 Comparison of terminal attitude errors when k is taken as different values

實驗結果表明，本文算法能夠實現回避基座可控空間機械臂的奇異，完成預期跟蹤任務。

4 結 論

1）與傳統的基于奇異分離和阻尼倒數的算法相比，本文算法可適用于不同自由度、不同空間構型的空間機械臂，并能夠以較小的跟蹤誤差完成機械臂的奇異回避，具備通用性。

2）通過合理設定各項參數，本文算法可以以不同的計算時間和跟蹤精度完成奇異回避問題的求解，使用者可以根據計算機性能進行權衡，選取適用于自己的參數取值。

3）由于本文算法采取在奇異區內分段規劃的策略對末端軌跡進行規劃，在期望末端位姿處在奇異區內時，機械臂仍能夠完成位姿跟蹤任務。