基于尖點突變模型的微波加熱固體介質的熱失控分析

楊彪，鄧卓，劉志邦，母其海，朱娜

(1.昆明理工大學信息工程與自動化學院，云南昆明，650500；2.昆明理工大學云南省人工智能重點實驗室，云南昆明，650500；3.昆明理工大學非常規(guī)冶金教育部重點實驗室，云南昆明，650093)

微波加熱作為一種新型的綠色冶金方法，通過微波在介質內部的介電損耗直接將能量選擇性地傳遞給被加熱介質的分子或原子，宏觀上表現出可選擇性加熱、加熱均勻、熱效率高、清潔無污染、啟動和停止加熱迅速等優(yōu)越特性。由于微波加熱具有獨特的優(yōu)勢，美國能源部已將微波加熱技術列為一種新能源和振興現代制造業(yè)的技術。在微波加熱過程中，隨溫度升高，會出現“熱失控”的宏觀現象。“熱失控”是微波與物料相互作用形成正反饋的結果，微波輸入功率的微小改變會導致被加熱物料溫度發(fā)生劇烈變化[1]。KENKRE等[2]研究了微波加熱陶瓷的溫度變化過程，并用經驗公式對該過程中溫度的急劇升高進行描述。KRIEGSMANN[3]建立了微波加熱陶瓷板的一維模型，在漸進分析的基礎上預測了物料溫度與微波輸入功率之間的關系，發(fā)現當物料電導率與溫度呈指數關系時，可描述為“S”形曲線。此后，該預測結果在許多理論研究中得到證明，但并未通過實驗方法證實。STUERGA 等[4]在微波加熱冷凍物體過程中，分析溫升曲線的斜率變化形式，為S形曲線提供了實驗依據。隨著對熱失控現象的深入研究，眾多研究者從不同角度對熱失控現象進行研究，并在微波加熱熱失控的控制研究方面取得了顯著成果[5-9]。由于熱失控發(fā)生時物料升溫很快，研究者們大多采用定性方法對該過程進行分析，對其定量研究相對較少，且溫度的“跳躍式”變化難以用傳統(tǒng)的微積分方法進行研究。本文作者將突變理論引入熱失控研究，并采用有限元方法進行數值模擬，實現微波加熱熱失控的定量分析。

突變理論是一門以現代控制理論和拓撲學為基礎，通過將突變現象用數學方式描述為7種基本初等突變，以解決非線性系統(tǒng)中不連續(xù)跳變問題的方法。其中，尖點突變模型使用最廣，具有突然跳躍性、滯后性、雙模態(tài)、不可達性和發(fā)散性等基本特點[10]。在尖點突變模型中，系統(tǒng)的控制變量和狀態(tài)變量構成系統(tǒng)的平衡曲面，系統(tǒng)在連續(xù)變化的控制變量作用下，其狀態(tài)變量會發(fā)生不連續(xù)的跳變，在圖形上表現為一個帶尖點的S 形曲面。尖點突變理論被廣泛應用于隧道[11-14]、邊坡[15-17]、巖土[18-19]、交通流模型[20-21]等多個領域，并能為其他領域突變現象的研究提供相應的理論基礎和研究依據。

本文基于微波加熱原理，通過將突變理論與微波加熱熱失控的產生機理相結合，構造出熱失控的尖點突變模型，分析尖點突變模型得到判斷加熱過程中溫度穩(wěn)定性的充要判據及臨界溫度表達式，從而實現對熱失控現象的定量研究。使用有限元方法，通過COMSOL Multiphysics軟件平臺模擬微波加熱碳化硅陶瓷過程，對尖點突變模型中的穩(wěn)定性判據進行數值計算，并結合臨界溫度表達式，從而實現微波加熱陶瓷介質熱失控的定量分析，進而判斷微波加熱系統(tǒng)的穩(wěn)定性。

1 微波加熱系統(tǒng)模型

1.1 物料的電磁特性

微波加熱過程涉及電磁場、溫度場及運動場在內的多物理場耦合、分布參數的非線性問題。其中，電磁場滿足Maxwell方程組，其微分形式表示如下：

式中：H為磁場強度，A/m；D為電位移，C/m2；E為電場強度，V/m；B為磁通量密度，Wb/m2；J為電流密度，A/m2；ρ為電荷密度，C/m3。H，D，E，B和ρ均為空間位置和時間的函數。

溫度場滿足的熱傳導方程表示如下：

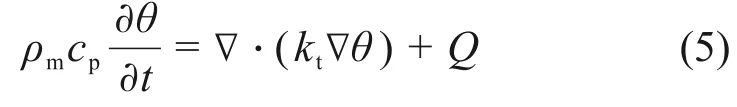
式中：θ為物料溫度；ρm和cp分別為物料的密度和比熱容；kt為熱傳導系數；Q為微波加熱過程中電磁功率的損耗。

微波加熱實質是微波穿透加熱物料，物料吸收微波能并將其轉化為熱能，從而實現快速加熱的過程。在此過程中涉及微波能的吸收與轉換。對于介質材料，考慮其在微波電磁場中的加熱效果與其介電特性密切相關，在電磁場中可用本構關系進行表示。描述電場、磁場及物料介電特性之間關系的本構方程表示如下[22]：

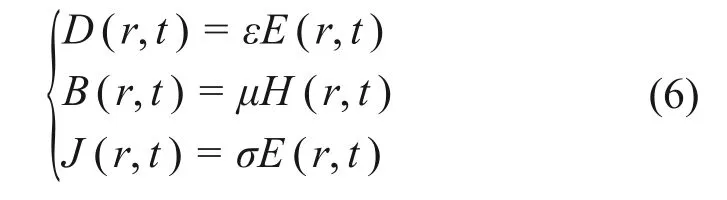
式中：ε，μ和σ分別為介電系數、磁導率和電導率，是影響微波加熱過程中物料升溫特性的物理參數。

由式(5)和式(6)可知：微波加熱中電場能和磁場能密切聯(lián)系，變化的磁場產生電，變化的電場產生磁，變化的電磁場相互激勵產生電磁波，波動過程在介電質中電磁能耗散直接轉換為熱能，進而提供加熱物料的熱源。同時，在電磁轉化過程中，物料的介電系數、磁導率和電導率影響著物料與微波電磁場相互作用的效果。

1.2 電磁特性對熱失控的影響

微波加熱物料實質上是電磁場與物料相互作用的過程。物料溫度升高導致介電損耗、電導損耗和磁損耗。對于本研究采用的碳化硅陶瓷固體，考慮其在加熱過程中無明顯磁化現象，忽略磁損耗的影響。在已有的文獻中，微波加熱陶瓷過程中大多只考慮陶瓷的介電損耗，本文根據碳化硅陶瓷的物理特性并結合陶瓷加熱的特點，同時考慮介電損耗和電導損耗。

當微波與物料接觸時，部分物料內部的極性分子在高頻電磁波的作用下不斷進行轉向極化而發(fā)生碰撞、摩擦，從而將微波能轉化為熱能，實現物料的加熱。在物料的極化損耗中，其吸收和轉化微波能的能力可用復介電常數ε*表示，即

式中：ε′為介電常數，表示物料吸收微波的能力；ε″為介電損耗，表示物料將吸收的微波能進一步轉化為熱能的能力；j為虛數單位。根據熱失控發(fā)生的機理，本研究重點考慮微波加熱過程中介電損耗(ε″)對熱失控的影響。

對于通過電導損耗產生熱量實現加熱的物料，在電場作用下將其吸收的電磁能量以傳導電流的形式轉化為熱能。因此，在電導損耗中主要考慮物料電導率σ對加熱的影響。

綜合上述分析，考慮到熱失控現象發(fā)生的難易，且研究所使用的陶瓷介質主要靠介電損耗和電導損耗來升溫，在文獻[23]與[24]中，使用指數函數模型[23]描述物料等效介電系數虛部與溫度的關系，使用冪函數模型[24]描述電導率與溫度的關系。因此，物料等效介電系數虛部ε″eff(θ)和電導率σ(θ)分別表示為：

式中：σ0為真空中的電導率；θ0為峰值溫度；γ，l1和l2為與介質物理性質、微波穿透深度、加熱過程的初始條件和邊界條件等有關的系數。

根據文獻[25]，l1和l2可分別表示為：l1=其中：Rz為物料在z軸上的高度，即物料的厚度；θe為環(huán)境溫度；ε(θe)和σ(θe)分別為環(huán)境溫度下的介電系數和電導率。

2 熱失控的尖點突變模型

2.1 微波加熱熱失控現象

通過能量守恒方程可以對熱失控現象進行描述，故式(5)可表示為

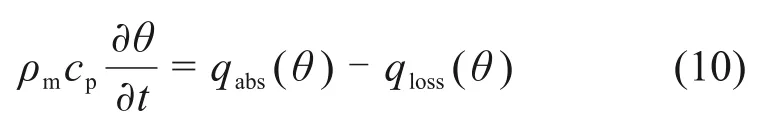
式中：qabs和qloss分別為產熱量和散熱量，表示微波加熱系統(tǒng)能量的變化量。因此，在某個臨界溫度時產熱大于散熱(即qabs＞qloss)，若繼續(xù)保持加熱則會出現熱失控現象。熱失控可以描述為在加熱過程中，微波與物料相互作用產生的熱量遠比散失的熱量多，此時，物料溫度急劇升高，為熱失控的產生創(chuàng)造了條件。

劉長軍等[26]基于FDTD 算法耦合求解Maxwell方程組和HTE 方程，完成微波加熱陶瓷板的數值模擬，其結果與GUPTA 等[27]的結論基本一致。根據數值計算得到的陶瓷板中心穩(wěn)態(tài)相對溫度(相對溫度其中，θ為物料溫度，θh為常溫)可知，溫度隨施加的微波功率不同呈現出S 形曲線變化趨勢。通過分析由功率和溫度組成的二維S 曲線可知，整條曲線分為上、中、下3 個部分。在上、下2個分支部分，溫度與功率呈現一一對應的關系；在中間分支部分，同一功率下對應3個不同的溫度點A1，A2和A3，表現為不穩(wěn)定的狀態(tài)。因此，溫度急劇變化發(fā)生在曲線的中間分支。數值計算獲取的S形曲線如圖1所示。

圖1 微波加熱過程S形曲線Fig.1 S-shaped curve of microwave heating process

由圖1可知：采用響應曲面法可將二維的S曲線拓展為三維的S曲面。對于S曲面的研究，根據影響熱失控的因素，并結合曲面特征可以將其用突變理論進行描述與研究。

2.2 微波加熱能量分析

考慮微波加熱過程中陶瓷固體介質通過介電損耗和電導損耗來實現快速加熱。通過介電損耗產生的熱量Q1表示為

式中：f為微波源頻率；|Eerm|為電場強度的均方根值[28]，為了方便后面計算，記|Eerm|為E。

通過電導損耗產生的熱量Q2表示為

因此，結合式(10)可將微波加熱過程中產生的總熱量Q表示為

2.3 尖點突變模型

熱失控是一種宏觀表現為被加熱物料溫度發(fā)生急劇變化的突變現象，在此過程中涉及能量的聚集。當同種物質能量聚集到一定值時，其能量會發(fā)生從連續(xù)量變到突然質變的變化過程，即發(fā)生突變。在微波加熱過程中，當微波能量在某一點富集到一定程度時，會使溫度快速上升，即產生失控現象。能量在聚集過程中，往往會在一些突出點內富集，這些富集的突出點會發(fā)生尖點效應，從而產生更大突變，為物料發(fā)生熱失控創(chuàng)造條件。因此，為了更好地定量研究熱失控現象，本研究采用尖點突變理論來對溫度變化進行研究，并通過尖點突變模型將熱失控現象以數學表達式的形式定量呈現出來。利用尖點突變理論進行微波加熱熱失控分析的具體實現過程包括如下7 個步驟。

1)根據微波加熱中物料吸收的總能量，建立加熱系統(tǒng)尖點突變模型的勢函數V(x)，并將其轉化為如下尖點突變模型的標準形式：

2)根據步驟1)所構造的勢函數，對其狀態(tài)變量x求一階導數并令其值為0，即可得到平衡曲面M的方程：

3)在步驟2)的基礎上，再次求導，即可得到奇點集S的方程：

4)聯(lián)立M和S的方程，消除x，即可得到突變的分叉集B的方程：

5)分析系統(tǒng)控制變量的變化情況并結合分叉集方程，可得微波加熱過程中溫度失穩(wěn)的充要判據，即必要條件為u＜0，充分條件為Δ≤0。同時，分析突變過程狀態(tài)變量的變化情況，可進一步推導得到熱失控的臨界溫度表達式。

6)在COMSOL Multiphysics軟件平臺中建立微波加熱SiC陶瓷介質的實驗模型，加熱一段時間并記錄陶瓷介質的溫度變化情況。根據陶瓷介質溫度的分布、變化情況及獲取的溫度數據，結合步驟5)的穩(wěn)定性充要判據及臨界溫度表達式即可判定系統(tǒng)的穩(wěn)定性，并得到熱失控臨界溫度。

7)根據穩(wěn)定性判據和臨界溫度表達式及仿真加熱過程的溫度變化情況，對比驗證尖點突變模型的有效性。

圖2 所示為根據上述步驟構造的尖點突變模型。由圖2 可見：由于系統(tǒng)狀態(tài)會發(fā)生突變，因此，整個平衡曲面可分為上葉、中葉和下葉3個部分，狀態(tài)變量x在控制變量u-v平面的投影Δ(即圖中AOB圍成的封閉區(qū)域)將整個控制變量空間分為穩(wěn)定區(qū)域(即Δ＞0)和突變區(qū)域(即Δ≤0)，分別對應平衡曲面的上下葉部分和中葉部分。當x位于穩(wěn)定區(qū)域時，系統(tǒng)在上葉或下葉發(fā)生平滑、穩(wěn)定變化，而當x由上葉(或下葉)運動到下葉(或上葉)時，將不經過中葉，而是在上、下葉之間發(fā)生“跳躍”式變化，即系統(tǒng)狀態(tài)發(fā)生突變。

圖2 尖點突變模型Fig.2 Cusp-catastrophe model

2.4 熱失控發(fā)生的理論判據

本研究選擇SiC陶瓷為加熱物料，將加熱過程中t時刻r處耗散的微波功率記為Q(r,t)，由式(13)可得

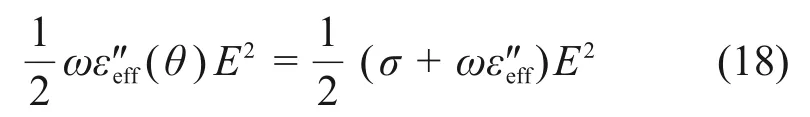
由突變理論可知系統(tǒng)狀態(tài)的變化趨勢可用勢函數表示，結合式(8)和式(9)，則物料溫度變化情況可表示為

平衡曲面方程為

對平衡曲面進行二次求導可得尖點，即

由式(21)可知，尖點處對應的物料溫度可表示為

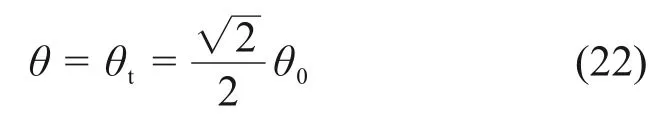
式(20)并不是標準形式，因此，需要將式(20)相對于尖點處的溫度作Taylor展開，并截取至3次項，化簡得

將式(23)進行變量代換，即可得到平衡曲面的標準形式：

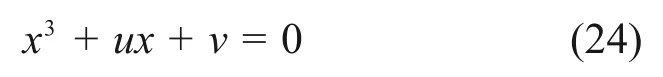
式中：

由式(28)可知，m與物料屬性及微波加熱的參數有關。聯(lián)立式(26)和式(27)，即可得分叉集方程：

經過分析可知，式(26)和式(29)可作為判斷加熱過程的熱穩(wěn)定判據。結合圖2可知，在熱失控尖點突變模型中，只有當u≤0時，系統(tǒng)狀態(tài)變量x才有可能與分岔集B相交，即發(fā)生突變。因而，發(fā)生突變的必要條件可表示為

式(24)為一個標準的一元三次方程，結合式(29)及方程的求根公式可知，當Δ= 0 且u＜0 時，狀態(tài)變量x會產生突變，其溫度變化率為：Δθ=因此，可得熱失控臨界溫度表達式：

式中：Di為物料第i層臨界溫度點。

3 模型有限元分析

微波加熱是一個復雜的物理過程，涉及電磁場、溫度場等物理場的耦合，在該過程中介質溫度的變化與系統(tǒng)幾何模型、介質物理屬性和介電特性等密切相關，呈現非線性、時變等特點，使用傳統(tǒng)方式難以對其進行準確研究。有限元方法是一種廣泛應用于解決復雜過程的數值計算方法，其基本思想是：在數值模擬軟件中，通過離散化方法將整個求解對象劃分為若干個小單元集合體，并根據小單元體的特性求解代數方程組，綜合分析各個小單元體的解，最終即得到整個求解區(qū)域的近似解。為了研究微波加熱過程固體物料溫度的變化對系統(tǒng)穩(wěn)定性的影響，本文采用有限元方法將整個復雜的物理求解域劃分為若干微小的單元，通過研究各個小單元在加熱過程中的溫度變化情況，并綜合分析即可近似得到整個物料的熱力學性質。同時，在分析過程中考慮本構關系、初始條件、邊界條件、介質的物理屬性和電磁特性等對系統(tǒng)穩(wěn)定性的影響。為了更好地進行數值模擬，選取第2節(jié)構造的尖點突變模型作為有限元分析的本構模型，并建立出微波加熱碳化硅固體介質的幾何模型。通過COMSOL Multiphysics軟件平臺，數值模擬出碳化硅陶瓷溫度隨時間的變化曲線，分析溫升特性曲線并結合熱穩(wěn)定判據即可實現微波加熱系統(tǒng)的穩(wěn)定性分析。

在微波諧振腔中加熱物料時，進行以下假設[29]。

假設1：加熱介質陶瓷為均勻同質；

假設2：僅考慮z軸方向上的溫度分布情況；

假設3：不考慮加熱過程中物料體積變化和相變；

假設4：xOy平面電場分布均勻。

此外，在加熱碳化硅陶瓷過程中，考慮到微波在諧振腔內不可能僅輻射于物料并被其完全吸收，將在腔體邊界會發(fā)生一部分透射，故存在阻抗邊界條件：

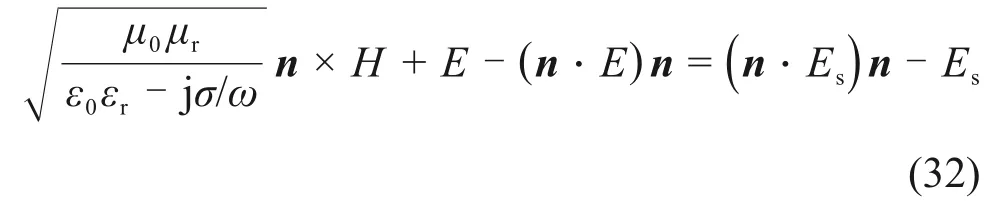
式中：μ0和ε0分別為真空磁導率、真空介電常數；μr和εr分別為相對磁導率、相對介電常數；ω為角頻率；n為單位法向量。

3.1 幾何模型

本文研究的微波加熱陶瓷的幾何模型如圖3所示。模型主要由微波加熱腔體、微波輸入端口和加熱物料組成。在加熱過程中，饋口使用BJ-26波導饋入頻率為2.45 GHz、功率為200 kW 的微波能量，微波諧振腔的長、寬、高分別為300，300 和200 mm，加熱時間為340 s，腔壁為銅。被加熱物料為正方體SiC 陶瓷片(邊長為50 mm)，將SiC 陶瓷放置在一個絕熱、不吸波、不反射波的“工”字形載物臺上，且載物臺長度、寬度、高度分別為80，40 和5 mm。為了實驗結果的準確性，需對幾何模型進行網格剖分，因此，本文定義最大單元邊長為24.74 mm，最小單元邊長為0.734 2 mm，網格劃分結果如圖4所示。

圖3 微波加熱系統(tǒng)幾何模型Fig.3 Geometric model of microwave heating system

圖4 加熱系統(tǒng)模型網格劃分Fig.4 Mesh generation of heating system

對于加熱物料SiC 陶瓷， 在COMSOL Multiphysics 軟件平臺中進行仿真加熱實驗時，需要根據其介電參數及物理屬性導入物料參數，從而進行仿真加熱實驗及有限元分析。SiC陶瓷的屬性參數如表1所示[30-31]。

表1 數值模擬中所用材料屬性Table 1 Properties of materials used in numerical simulation

3.2 模擬計算與結果分析

微波激勵源頻率為2.45 GHz，求解設定加熱時間為0～340 s，通過數值計算可得陶瓷介質整體溫升特性曲線如圖5 所示。選取340 s 時的溫度分布三維視圖進行分析，如圖6 所示。由圖5 和圖6可知：在開始階段，陶瓷在微波電磁場作用下溫度平穩(wěn)升高，物料表面溫度分布均勻，體現了微波均勻加熱的特點。由于微波加熱具有選擇性加熱的特點，物料不同部分、不同位置的溫度分布逐漸呈現不均勻性，其中，上、下表面溫度較高，而中間部分溫度相對較低，這與物料對微波的吸收能力及微波的穿透深度等因素有關。

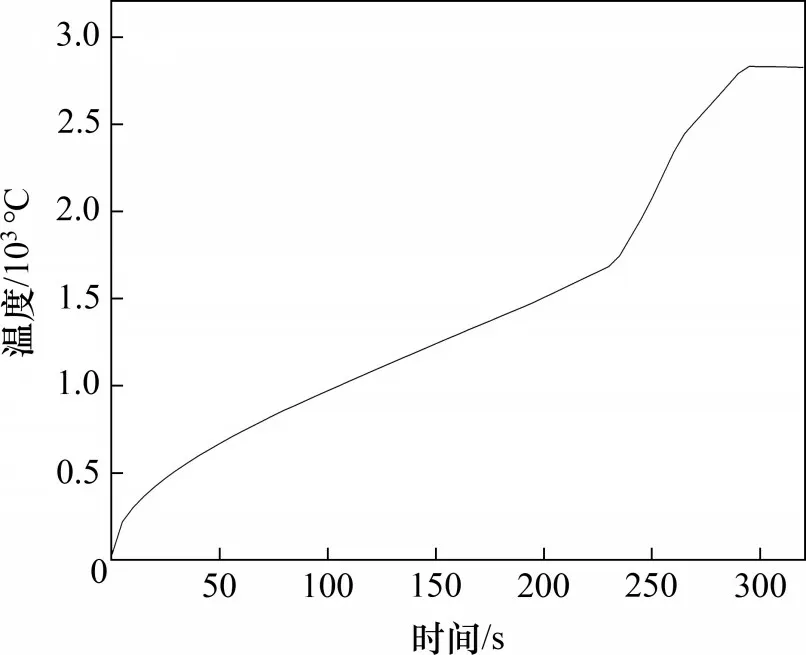
圖5 碳化硅陶瓷整體升溫特性曲線Fig.5 Overall temperature rise characteristic curve of SiC ceramic

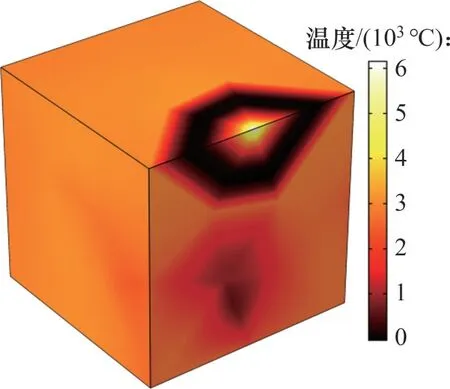
圖6 加熱340 s時微波場內陶瓷表面溫度分布Fig.6 Temperature distribution of ceramic surface in microwave field when heated for 340 s

本文選擇截取加熱時間為340 s 時，對物料上表面、中間截面及下表面進行研究，選取物料中心位置處作為坐標原點，3個截面的溫度分布如圖7 所示。此外，由于熱失控表現為局部熱點，因此，在3 個截面中分別選擇點F1，F2和F3進行分析，其溫升特性曲線如圖8所示。

由圖7和圖8可知：在微波加熱碳化硅陶瓷過程中，物料溫度分布不均勻，上、下表面存在較為明顯的熱失控現象，表現為部分區(qū)域溫度快速升高，而對于中間截面部分，溫度呈現穩(wěn)定上升趨勢。

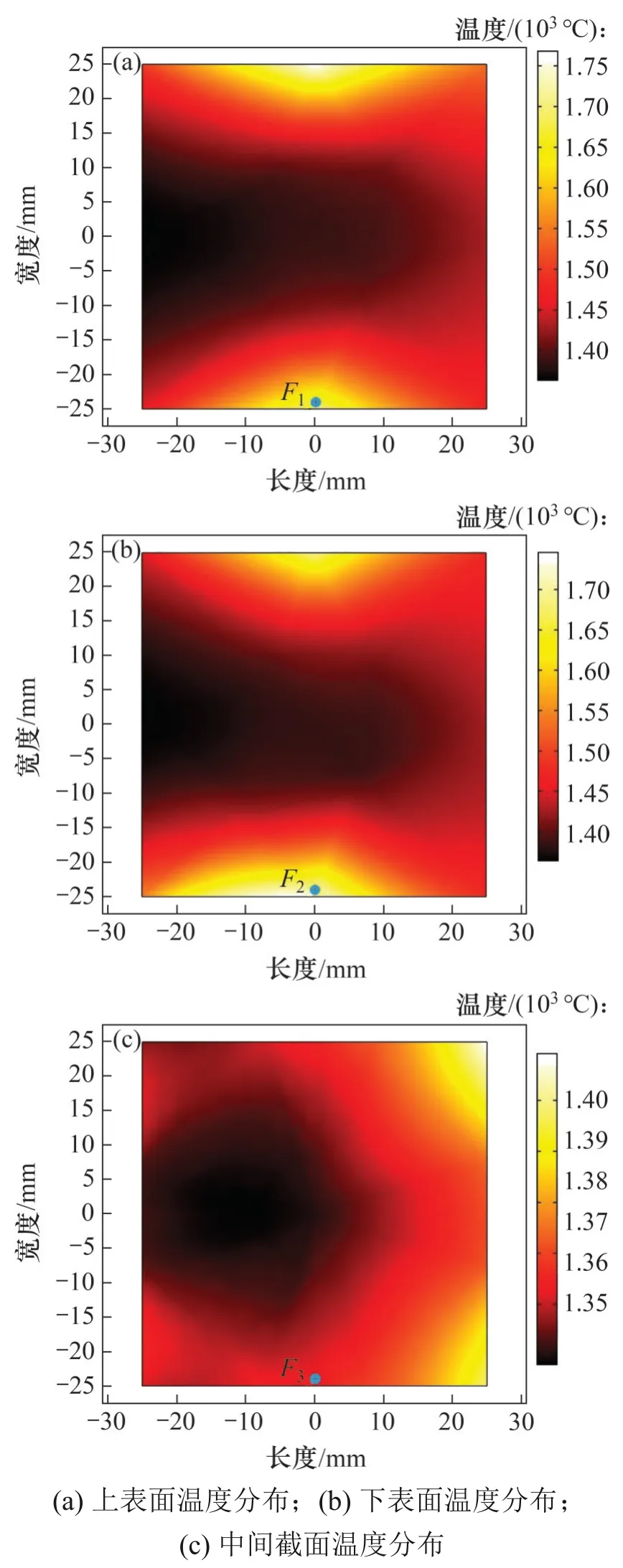
圖7 340 s時3個截面的溫度分布Fig.7 Temperature distributions of three cross sections at 340 s

圖8 3個截面選定點的溫升特性曲線Fig.8 Temperature increase characteristic curves of selected point at three cross sections

記陶瓷板溫升曲線溫度發(fā)生急劇升高的點為Di，最高溫度點為Ei，其中，i取1和2，則上、下截面Di溫度分別為1 768 ℃和1 746 ℃。在COMSOL 仿真中，通過有限元分析考慮被加熱物料的物理屬性、微波穿透深度、系統(tǒng)初始條件和邊界條件等，并結合文獻[25]可知，微波加熱SiC陶瓷時γ取-4，l1和l2的取值滿足l2/l1=4.57×108是合理的。因此，可通過對截面定量分析來判斷系統(tǒng)的穩(wěn)定性。

對于上截面點F1而言，由溫升特性曲線可知，從235 s開始，溫度急劇上升，加熱至295 s，溫度出現最大值，即θ0=2 943 ℃，根據2.4 節(jié)，結合式(26)～(31)可知，u≈-5，Δ≈-475.0，由穩(wěn)定性判據可知，u＜0，Δ＜0 時，發(fā)生熱失控。根據第2節(jié)突變理論的相應推導，可通過式(21)，(27)和(31)得到此時熱失控的臨界溫度，即

同理，對于下截面點F2，從235 s 開始，溫度急劇上升，加熱至295 s，溫度出現最大值，即θ0=2 832 ℃，根據穩(wěn)定性判據可知，u≈-4.84，Δ≈-472.6，此時存在熱失控現象。相應地，此時熱失控的臨界溫度表示為

對于中間截面點F3，同樣選擇235 s 時的溫度進行研究。 此時，u≈-2 ＜0，v≈1.5 ＞0，Δ≈28.8 ＞0，結合穩(wěn)定性判據可知，沒有發(fā)生熱失控現象。

根據上述分析可知，溫度數值計算結果與實驗模擬結果中的點Di對應的溫度接近，表明理論計算結果與有限元分析結果接近，通過尖點突變方法能對熱失控現象進行定量研究。

4 結論

1)根據熱失控的發(fā)生機理，通過對微波加熱過程進行能量分析并結合加熱介質的電磁特性及物理屬性，構造出定量描述熱失控現象的尖點突變模型。分析突變模型并推導得到判斷加熱穩(wěn)定性的充要判據及臨界溫度表達式。

2)采用COMSOL Multiphysics軟件平臺構造微波加熱SiC陶瓷的幾何模型，綜合考慮系統(tǒng)的初始條件、邊界條件及物料的物理屬性、微波穿透深度及電磁特性，可對陶瓷介質進行有限元分析。通過分析物料上表面、中間截面和下表面的溫度分布情況及溫升特性曲線，發(fā)現陶瓷上、下表面溫度在235 s 時急劇上升，經過60 s 加熱，溫度分別從1 768 ℃和1 746 ℃升至穩(wěn)定最高溫度2 943 ℃和2 832 ℃，而中間截面溫度穩(wěn)定升高。

3)結合加熱穩(wěn)定性判據和臨界溫度表達式對加熱過程進行定量分析可知，上、下表面Δ均小于0，分別為-475.0 和-472.6，u分別為-5.0 和-4.8，中間截面Δ為28.8，u為-2，說明物料在加熱過程中溫度分布不均勻，物料表面存在熱失控現象，溫升速率變化較大且溫度相對較高，而中間溫度升高較為平穩(wěn)，溫度相對較低。上、下表面臨界溫度分別為1 700 ℃和1 685 ℃，與有限元分析結果相吻合。定量分析結果驗證了本研究提出的熱失控尖點突變模型的有效性與可行性。