基于SSA-Elman神經網絡的電離層TEC短期預報模型

湯 俊 鐘正宇 李垠健 高 鑫

1 華東交通大學土木建筑學院，南昌市雙港東大街808號，330013

電離層作為近地空間環境的重要組成部分，其發生的任何細微變化都有可能對導航定位系統、無線電傳播與通訊、測量及人類空間活動產生重大影響[1]。衛星信號的傳播誤差與電離層總電子含量直接相關，提高電離層TEC短期預報精度可以有效提高導航定位精度。目前電離層TEC短期預報主要有數理統計和人工智能兩種方法。由于TEC具有隨時間發生周期性變化的特點，國內有關TEC預報的研究多以數學統計法中的時間序列分析為主[1-4]。

人工智能法則以神經網絡模型為代表，相較于時間序列分析方法，神經網絡模型具有更高的預報精度及計算速度[5-7]。電離層在時空上的隨機性和不平衡性使TEC具有非線性和不平穩的特點[8]，由于神經網絡能夠以任意精度逼近任意N維到M維映射，從而達到預報效果，其作為一種典型的非線性預報模型可有效預報電離層TEC。許多學者采用神經網絡模型對TEC進行有效預報，然而神經網絡在參數選擇及網絡優化等方面較為復雜，且存在過度擬合導致精度下降的情況，群優化算法可有效改善該缺陷。因此，本文提出一種群優化算法改進Elman神經網絡的電離層TEC短期預報模型。

1 模型算法原理

1.1 BP神經網絡和Elman神經網絡

BP神經網絡是一種按照誤差逆向傳播算法訓練的多層前饋神經網絡[9]。相比于BP神經網絡的3層結構，Elman神經網絡在隱含層上增加一個承接層，可以記憶隱含層前一時刻的輸出，使系統具有適應時變特性的能力。

1.2 SSA-Elman組合模型

目前，國內外已有很多有關群優化算法的研究，許多學者提出一些性能優異的群優化算法，其中粒子群算法(particle swarm optimization, PSO)和蟻群算法(ant colony optimization, ACO)最具代表性。與粒子群算法和蟻群算法相比，麻雀搜索算法(SSA)[10]具有良好的穩定性和收斂速度，并具有探索未知區域和避免陷入局部最優的能力。

SSA-Elman組合模型將SSA尋優獲得的最優初始權值和閾值賦值給Elman神經網絡，在Elman神經網絡迭代過程中通過計算網絡誤差，進一步更新Elman神經網絡的權值和閾值，當滿足精度要求后則可以進行電離層TEC預報。

1.3 模型參數及處理

電離層TEC受地磁活動、太陽活動及引力波等因素影響，隨晝夜、季節變化而發生周期性變化。本文在建立電離層TEC預報模型時，選取地磁活動指數Dst及TEC作為輸入參數，其中地磁活動指數是描述一個時段內地磁擾動強度的分級指標[9]。

在使用BP神經網絡進行TEC預報時，選取1個輸入層、1個隱含層和1個輸出層的3層網絡結構，將最大學習次數設置為5 000，學習速率設置為0.01，期望誤差設置為0.000 1。Elman神經網絡和SSA-Elman組合神經網絡參數設置與BP神經網絡保持一致，通過調整參數，將SSA種群數量設置為20，最大迭代次數為30，發現者占種群總數20%，安全系數設置為0.8，進行預警行為的個體數量為3。采用15 d預報5 d的方法對電離層TEC進行預報，其中網絡訓練樣本選取前15 d的TEC及Dst作為網絡的輸入層，后5 d的TEC及Dst作為網絡的輸出層進行網絡訓練，并分別對TEC及Dst進行歸一化處理，將數值控制在[-1, 1]范圍內以便于網絡訓練。

2 實驗與分析

本文所用數據來源于CODE中心，時間分辨率為1 h，選取2018年全年低中緯度地區(5°N, 120°E)和(40°N, 120°E)的TEC數據進行實驗分析。圖1(a)和1(b)分別為(5°N, 120°E)和(40°N, 120°E)處全年的電離層TEC變化趨勢，圖1(c)為2018年全年的地磁活動指數。通過對比可以發現，當地磁活動指數發生擾動時，對應TEC也會發生明顯變化，TEC與地磁活動指數具有較強的相關性。選取均方根誤差(RMSE)、殘差(Δ)及相關系數(ρ)用于分析比較，計算公式參見文獻[8]。

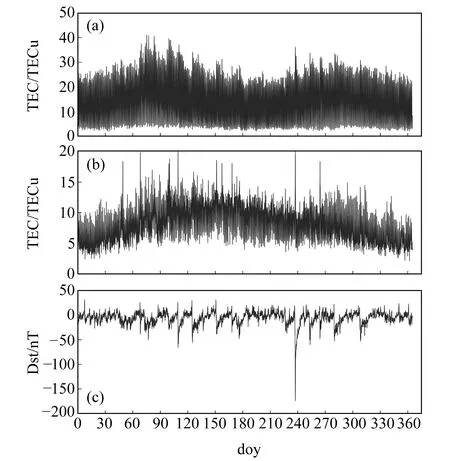
圖1 2018年電離層TEC及地磁活動指數

2.1 平靜期

選取平靜期對應時段，圖2為doy205～209對應的地磁活動指數，從圖中可以看出，該時間段Dst指數都維持在-20～20 nT范圍內，均大于-30 nT。

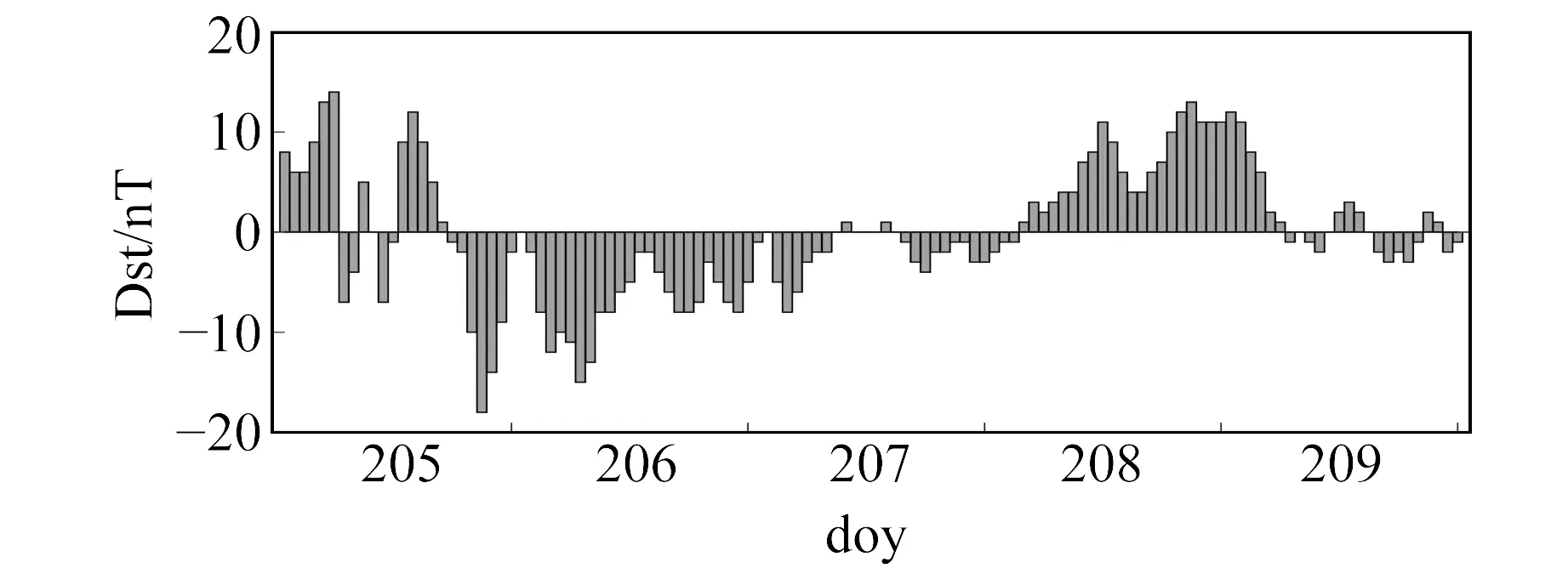
圖2 平靜期地磁活動指數

圖3為利用3種模型預報不同緯度的TEC，其中圖3(a)和3(b)分別對應低緯度和中緯度。從圖3(a)可以看出，低緯度的TEC變化較為平緩，3種模型預報值的變化趨勢相近，但SSA-Elman組合模型的預報值相比BP模型和Elman模型更加接近實測值，SSA-Elman組合模型在峰值處和谷值處的預報效果優于另外2種模型。從圖3(b)來看，不同于低緯度TEC平緩的變化趨勢，中緯度TEC在峰值處出現突變，因此突變處的擬合程度可作為模型精度的評價指標之一。BP模型的預報值明顯偏離TEC實測值，在doy207出現極端峰值，Elman模型和SSA-Elman組合模型對峰值處的預報效果優于BP模型，但從圖中可以明顯看出，Elman模型的殘差大于SSA-Elman組合模型。綜上所述，SSA-Elman組合模型和Elman模型的預報效果明顯優于BP模型，SSA-Elman組合模型的預報精度相較Elman模型具有一定程度的提高。

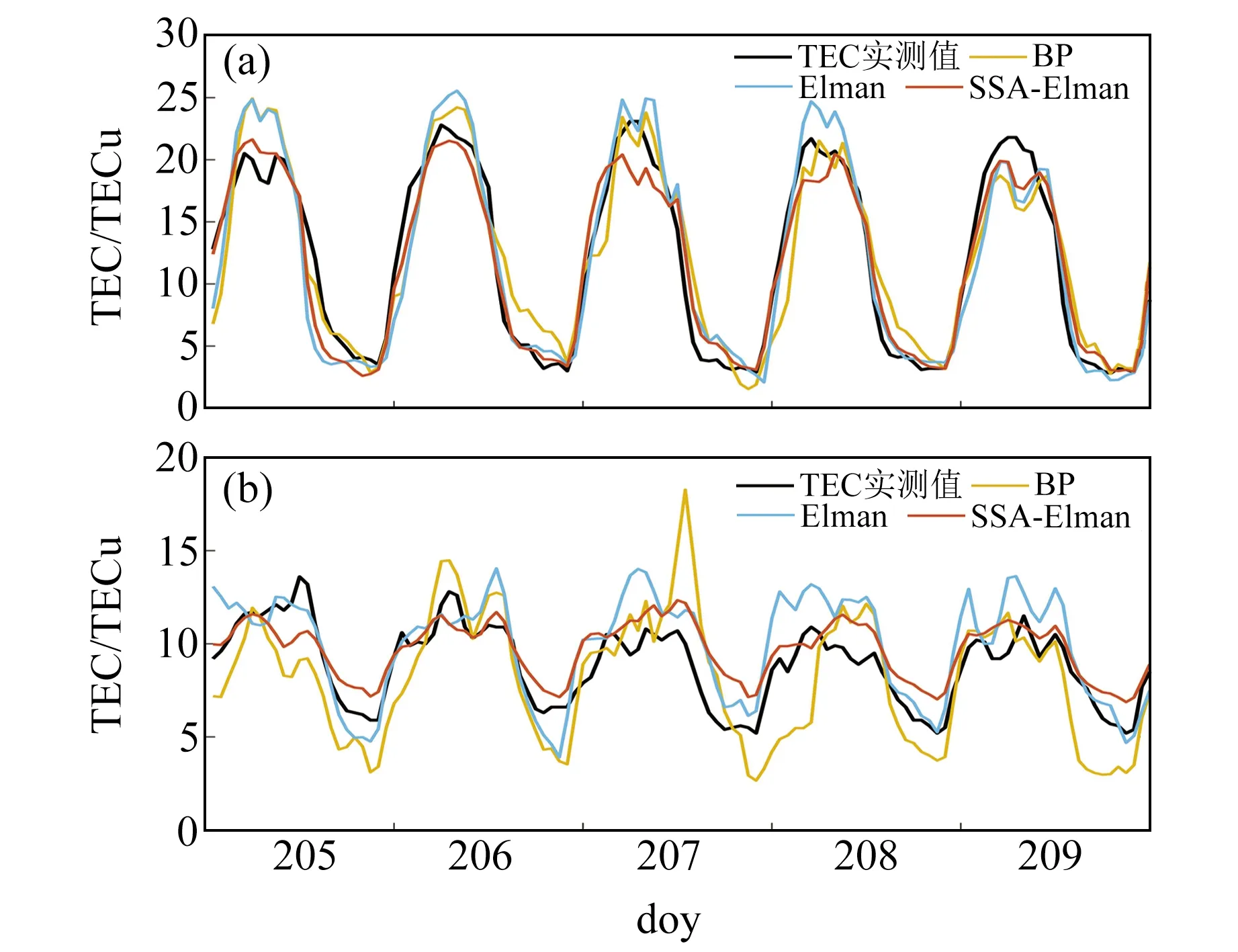
圖3 平靜期3種模型TEC預報值與實測值對比

評價模型精度的另一項指標為殘差(Δ)，圖4為平靜期3種模型TEC預報殘差值對比情況，其中圖4(a)和4(b)分別對應低緯度和中緯度。從圖4(a)可以看出，SSA-Elman組合模型的預報殘差值基本在4 TECu以內，最大殘差接近6 TECu，Elman模型的預報殘差值多數集中在4～6 TECu之間，BP模型的部分預報殘差值高達8 TECu，預報誤差最大。同時，BP模型和Elman模型的殘差值分布相較SSA-Elman組合模型更為離散，BP模型的殘差值分布在3種模型中最為離散，該現象在中緯度情況下更加明顯。使用SSA-Elman組合模型預報得到的殘差值絕對值基本在3 TECu以內，Elman模型在4 TECu以內，而BP模型最大殘差值可達9 TECu，其殘差值在doy207、208、209比其他2個模型多出將近4 TECu，離散程度大于Elman模型和SSA-Elman組合模型。因此，BP模型預報精度最差，總體誤差大于其他2個模型，SSA-Elman組合模型相比Elman模型精度更優。

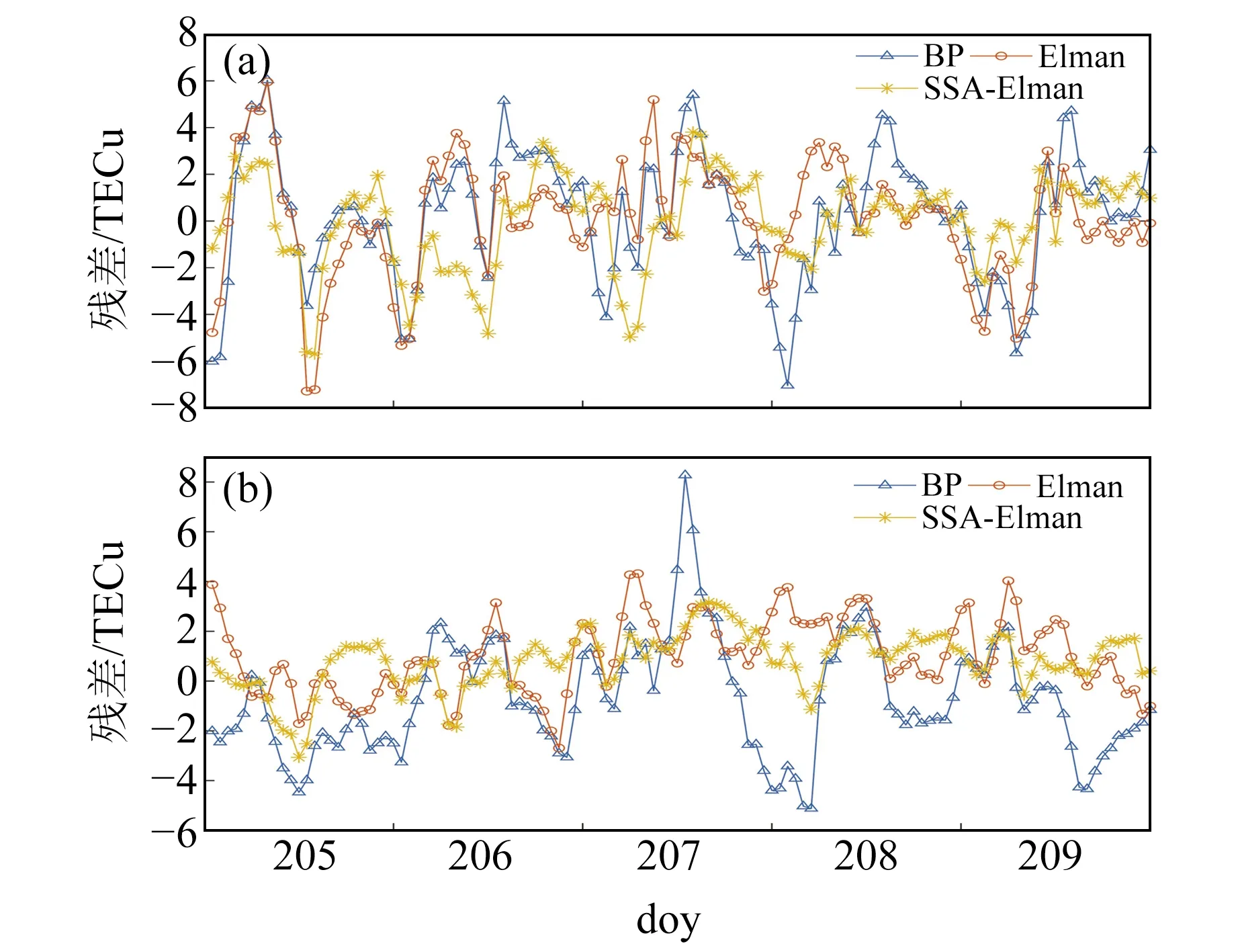
圖4 平靜期3種模型TEC預報殘差值對比

表1為中低緯度地區doy205～209期間3個模型預報結果的均方根誤差(RMSE)、殘差(Δ)及相關系數(ρ)對比結果。由表可知，對平靜期進行5 d 的低緯度TEC預報時，BP模型5 d的RMSE平均值為2.763 TECu，殘差平均值為2.218 TECu，相關系數為0.929；Elman模型5 d的RMSE平均值為2.402 TECu，平均殘差為1.876 TECu，相關系數為0.946；SSA-Elman組合模型5 d的RMSE平均值為1.776 TECu，平均殘差為1.382 TECu，相關系數為0.972。對中緯度地區TEC進行預報時，BP模型5 d的RMSE平均值為2.360 TECu，平均殘差為1.974 TECu，相關系數為0.837；Elman模型5 d的RMSE平均值為1.785 TECu，平均殘差為1.468 TECu，相關系數為0.887；SSA-Elman組合模型5 d的RMSE平均值為1.358 TECu，平均殘差為1.168 TECu，相關系數為0.904。從上述分析可知，SSA-Elman組合模型的3個評價指標均優于其他2個模型，預報精度最優。

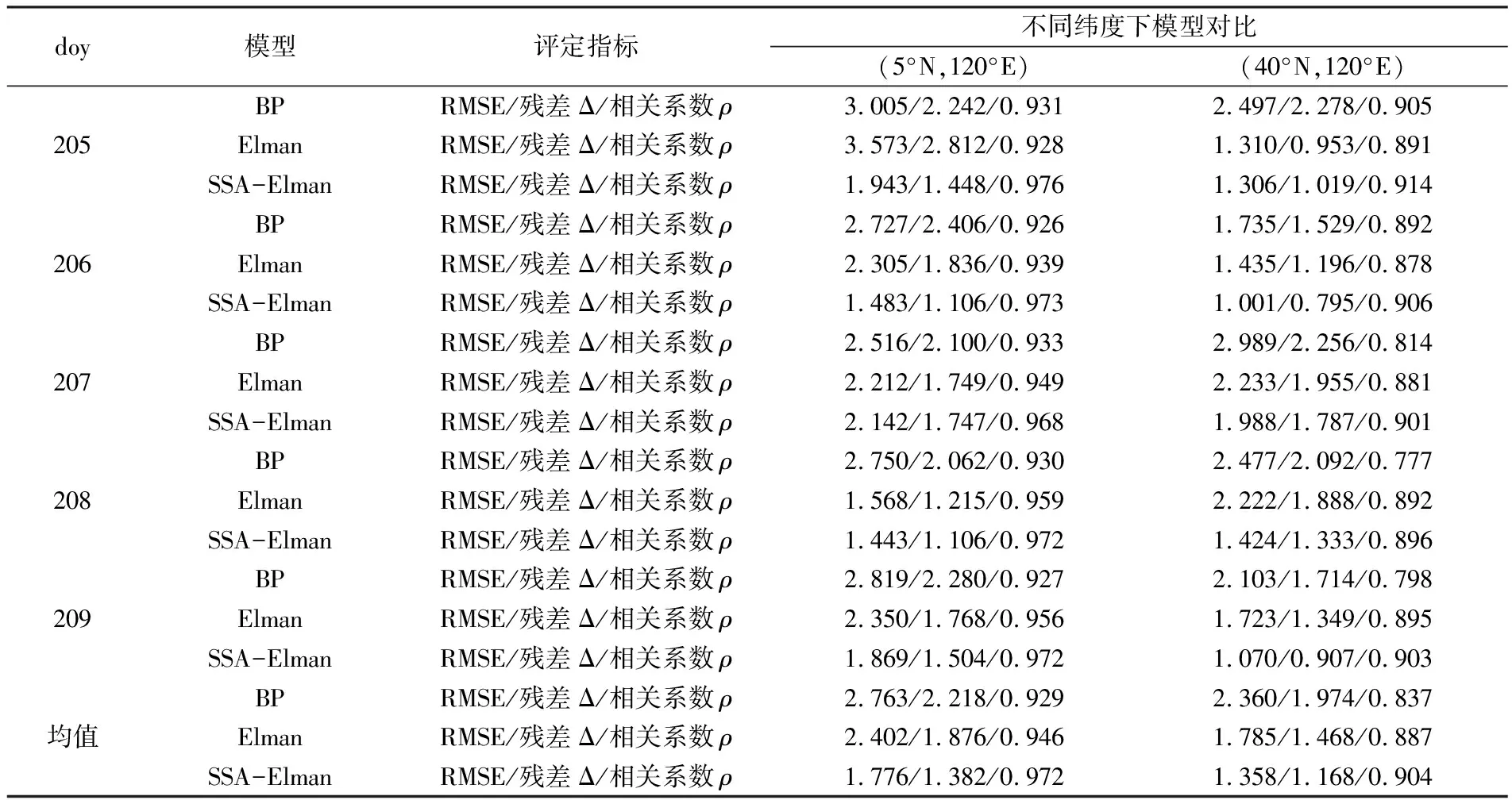
表1 平靜期不同緯度下3個模型預報指標對比

2.2 擾動期

圖5為doy236～240對應的地磁活動指數，從圖中可以看出，該時間段Dst指數在-180～20 nT范圍內變化，根據國際磁暴劃分標準，這5 d發生較大磁暴，與平靜期Dst指數相比，擾動期Dst指數跨度極大，正負峰值相差近200 nT。

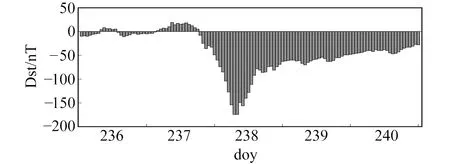
圖5 擾動期地磁活動指數

圖6為擾動期中低緯度TEC實測值與3種模型TEC預報值對比結果，其中圖6(a)和6(b)分別為低緯度和中緯度處TEC變化趨勢。由圖6(a)可知，BP模型相比其他2種模型在doy237出現極端值。由于受磁暴影響，doy238中低緯度TEC實測值遠大于其他4 d，3種模型在該天的預報殘差均較大。BP模型和Elman模型的預報值在doy236谷值處出現突變，與之相比，SSA-Elman組合模型的預報值變化更平緩，且預報值更加接近實測值，預報效果相比其他2種模型更好。從圖6(b)來看，與低緯度TEC相比，中緯度TEC在峰值處存在突變，BP模型在谷值處的預報結果呈現出與實測值相反的變化趨勢。此外，Elman模型與SSA-Elman組合模型在峰值處的擬合度優于BP模型，且SSA-Elman組合模型比Elman模型的預報殘差值更小。由此可知，SSA-Elman模型在中緯度和低緯度地區均具有更高的預報精度。

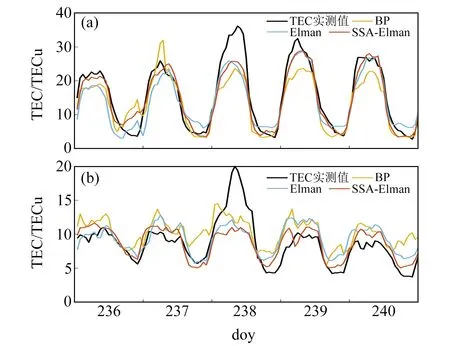
圖6 擾動期3種模型TEC預報值與實測值對比

圖7為擾動期3種模型TEC預報殘差值對比，其中圖7(a)和7(b)分別對應低緯度和中緯度。從圖中可以看出，低緯度的預報殘差值為中緯度的2倍，中低緯度在doy238的TEC預報殘差值均發生較大波動。由于當日受磁暴影響，Dst指數低至-174 nT，導致3種模型的預報殘差值均較大。利用BP模型預報其余4 d低緯度TEC時，最大殘差接近12 TECu，而利用Elman模型與SSA-Elman組合模型預報時，殘差值均小于8 TECu，因此BP模型在低緯度的預報效果在3種模型中最差。在中緯度地區，BP模型預報其余4 d的殘差值在0.5～7 TECu范圍內波動，Elman模型的預報殘差值在2～4.5 TECu范圍內波動，SSA-Elman組合模型的預報殘差值在2～4 TECu范圍內波動，由此可見，BP模型在中緯度的預報效果不如其他2種模型。

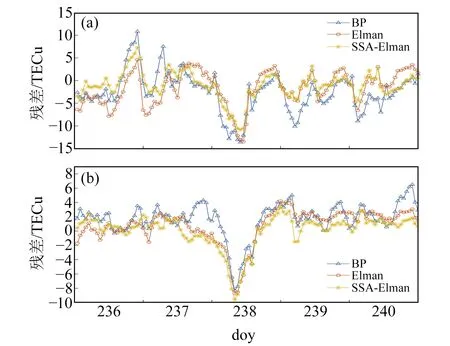
圖7 擾動期3種模型TEC預報殘差值對比

由于圖7中Elman模型和SSA-Elman組合模型預報殘差值的變化趨勢相似，殘差值大小相近，為分析2種模型的預報精度，表2為中低緯度地區doy236～240期間3個模型預報結果的均方根誤差(RMSE)、殘差(Δ)及相關系數(ρ)對比結果。由表可知，對擾動期進行5 d的低緯度TEC預報時，BP模型5 d的RMSE平均值為4.775 TECu，平均殘差為3.803 TECu，相關系數為0.883；Elman模型5 d的RMSE平均值為3.945 TECu，平均殘差為3.237 TECu，相關系數為0.924；SSA-Elman組合模型5 d的RMSE平均值為2.955 TECu，平均殘差為2.372 TECu，相關系數為0.952。對擾動期進行5 d的中緯度TEC預報時，BP模型5 d的RMSE平均值為2.846 TECu，平均殘差為2.446 TECu，相關系數為0.749；Elman模型5 d的RMSE平均值為2.255 TECu，平均殘差為1.988 TECu，相關系數為0.803；SSA-Elman組合模型5 d的RMSE平均值為1.896 TECu，平均殘差為1.586 TECu，相關系數為0.826。3種模型擾動期TEC預報精度均低于平靜期，BP模型的相關系數低于0.8，預報效果最差，SSA-Elman組合模型的預報效果優于Elman模型，其對電離層擾動期TEC的預報效果相較Elman模型具有一定程度的提高。

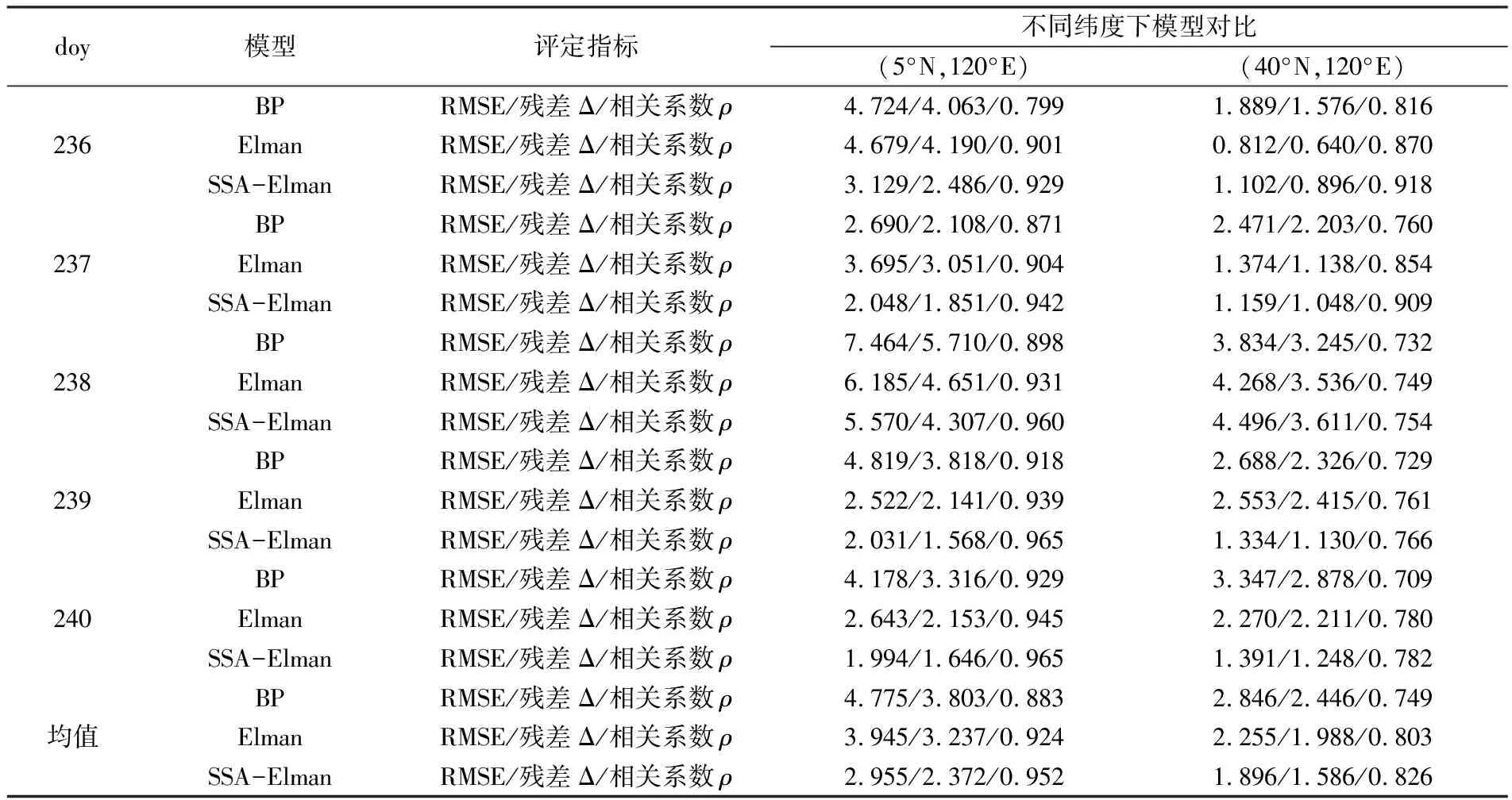
表2 擾動期不同緯度下3個模型預報指標對比

2.3 不同經度地區模型精度驗證

為進一步驗證模型在不同經度地區預測值的可靠性，利用CODE中心提供的2018年(5°N,120°W)和(40°N,120°W)處TEC值，使用3種預報模型進行建模，并利用中科院提供的同位置、同時段TEC作為實測值進行精度驗證。表3為3種模型在平靜期(doy205～209)和擾動期(doy236～240)均方根誤差(RMSE)、殘差(Δ)和相關系數(ρ)的均值。從表中可以看出，使用SSA-Elman組合模型對平靜期和擾動期進行低緯度TEC預報時，預報精度均優于BP模型和Elman模型，其中平靜期的RMSE為1.970 TECu，殘差為1.499 TECu，相關系數為0.984；擾動期的RMSE為3.818 TECu，殘差為2.702 TECu，相關系數為0.934。對中緯度TEC進行預報時，平靜期SSA-Elman組合模型的RMSE為1.640 TECu，殘差為1.402 TECu，相關系數為0.900，優于BP模型和Elman模型；擾動期SSA-Elman組合模型的RMSE為2.347 TECu，殘差為 1.928 TECu，相關系數為0.916，優于BP模型和Elman模型。經過對比分析可知，SSA-Elman組合模型可對中低緯度不同經度地區的TEC進行有效預報，且預報效果優于BP模型和Elman模型。

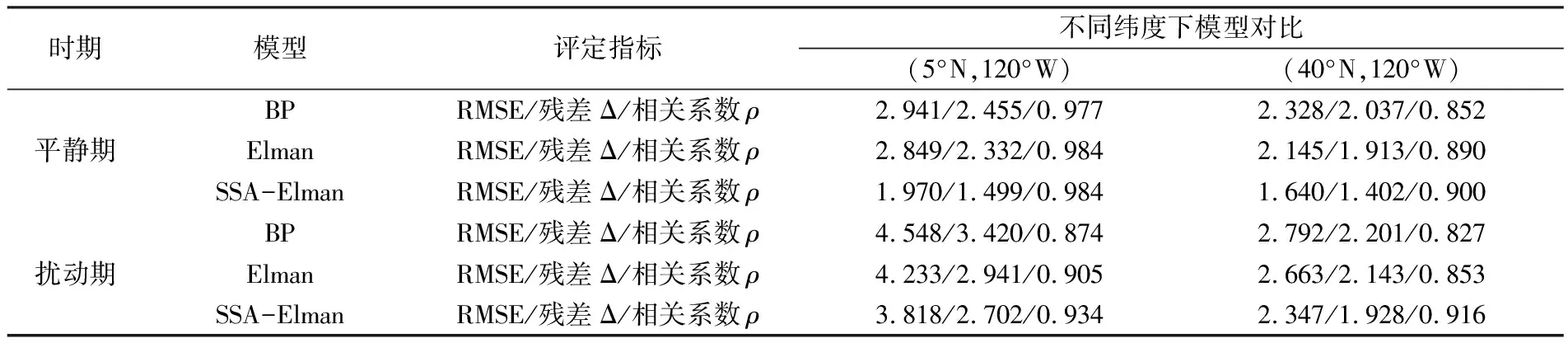
表3 120°W處不同緯度地區3個模型預報指標對比

3 結 語

根據電離層TEC序列非線性和不平穩的特點，針對傳統BP神經網絡模型在對TEC進行預報時易陷入局部最優的缺陷，本文選取網絡全局穩定性更強并具有適應時變特性能力的Elman神經網絡模型，利用麻雀算法對Elman模型進行優化，構建SSA-Elman組合模型。采用地磁活動指數Dst及TEC作為輸入，分別對中低緯度平靜期和擾動期電離層TEC進行5 d的短期預報，并將其與BP神經網絡模型及Elman神經網絡模型的預報效果進行對比分析。結果表明，SSA-Elman組合模型具有更好的預報效果。由于TEC不僅受地磁活動影響，還會受到諸如太陽風、引力波等因素影響，并且在不同時間、空間條件下進行預報存在不穩定性，隨著預報時長的增加，個別時段還存在預報精度下降的問題，可嘗試使用更多的數據進行訓練以提高網絡的泛用性，或將太陽風、引力波等參數加入到模型訓練中以提高預報的準確度。