長三角地區多種大氣可降水量獲取方法研究
李 黎 高 穎 陳國棟 趙 偉
1 蘇州科技大學地理科學與測繪工程學院,蘇州市學府路99號,215009 2 蘇州科技大學北斗導航與環境感知研究中心,蘇州市學府路99號,215009
大氣可降水量(precipitable water vapor, PWV)作為反映水汽含量的重要指標,與實際降水之間具有較高的相關性,在描述水汽含量、監測和預報天氣變化等方面具有重要意義。Bevis等[1]提出利用GPS技術獲取高時空分辨率的GPS-PWV;石小龍等[2]研究發現GPS-PWV能夠較好地反映水汽含量的時空分布變化;向玉春等[3]研究發現,與探空法相比,地面氣象資料推算的PWV偏差較小,而GPS-PWV偏差較大;盧士慶等[4]將部分求解PWV的方法進行比較發現,GPS-PWV精度較高且不受天氣狀況影響,具有廣闊的應用前景,而基于地面露點資料計算PWV方法簡便且可以得到實時結果;翟樹峰等[5]提出一種基于GPT2w獲取Tm,進而利用地基GPS反演PWV的方法,該方法獲取的PWV精度與基于Bevis-Tm反演的PWV精度相當。本文利用探空資料、地面露點資料、GNSS數據以及GPT3模型[6]計算長三角地區PWV,并以探空法計算得到的PWV為參考評估其他方法,從精度、可靠性和時效性等方面比較分析以上各方法。
1 數據來源及處理方法
1.1 數據來源
實驗數據主要來自2017年長三角地區7個探空站和2個GNSS基準站,位置信息如表1所示。由表1可知,射陽GNSS站與探空站經緯度完全一致,安慶GNSS站與探空站位置非常接近,因此GNSS站與探空站之間的差異主要為高程差,安慶和射陽兩站高程差分別為51.6 m和28.3 m。為確保GNSS-PWV與探空PWV精度對比的可靠性和準確性,進一步利用靜力平衡方程分析GNSS站與探空站高程差對PWV的影響。結果表明,安慶和射陽GNSS站與探空站之間高程差對PWV的誤差影響分別為1.3 mm和0.7 mm,影響程度較小,因此可以直接利用探空站PWV評估GNSS-PWV和其他方法得到的PWV精度。
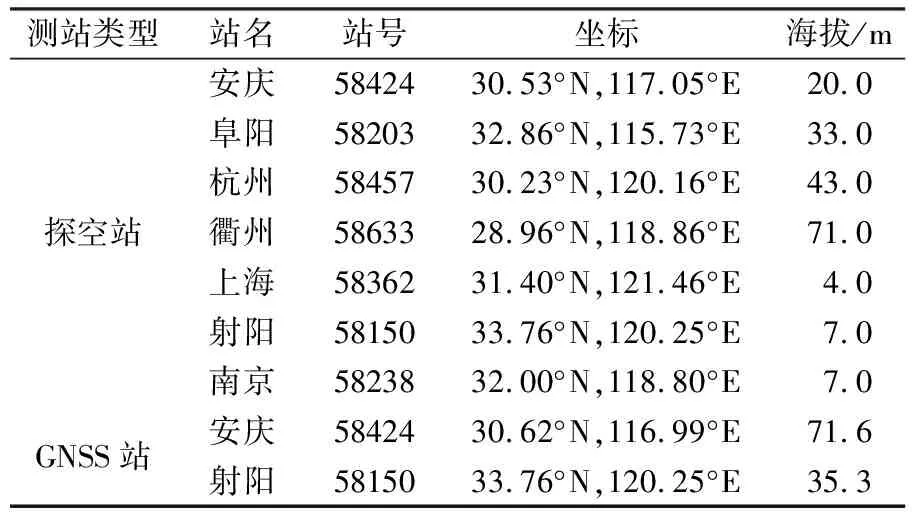
表1 長三角地區7個探空站及2個GNSS站位置信息
1.2 Tm計算方法
采用探空數據和數值積分法獲取的Tm精度較高,可作為參考值對其他方法獲取的Tm進行評估,其計算公式為:
(1)
式中,z為分層高度,e為地面水汽壓,可通過2008年世界氣象組織提出的飽和水汽壓公式計算得到。
1.3 PWV計算方法
1.3.1 基于探空資料
PWV是指單位面積空氣柱內所含的水汽總量,計算公式為:
(2)
式中,q為各氣壓層空氣比濕,p為對流層上界氣壓,P0為地面氣壓。
1.3.2 基于地面氣象資料
建立PWV與地面露點資料之間的關系可為缺乏探空數據的地區獲取PWV提供新途徑,本文分別采用楊景梅等[7]和張學文[8]建立的經驗關系式反演PWV。
綜上所述,三部作品雖敘述的故事有類似之處,且基本主題都是青年一代反對封建家長、封建禮教,追求愛情的幸福,但由于時代不同,意識形態、哲學思想的影響不同,人們的認識有了很大的不同,尤其是曹雪芹,思想的深邃使同樣的故事有了深廣的文化意蘊,是質的飛躍。
文獻[7]基于地面露點溫度、高程和緯度建立的PWV經驗關系式為:
(3)
文獻[8]建立的PWV與水汽壓(根據露點溫度計算)的關系式為:
PWV=1.74e
(4)
1.3.3 基于GNSS數據
利用精密單點定位技術可解算GNSS站觀測數據,從而獲取高精度的GNSS-ZTD。其中ZHD可根據Saastamonien模型[9]獲取:
(5)
式中,Pc、φc和Hc分別為測站氣壓、緯度和海拔。
GNSS-PWV與ZWD(ZWD=ZTD-ZHD)的關系式為:
(6)
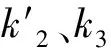
1.3.4 基于GPT3模型
基于歐洲中期天氣預報中心(ECMWF)數據建立的對流層延遲模型GPT3是獲取PWV所需氣象參數的有效方法之一,其計算公式為:
(7)
式中,r(t)為格網點處氣象參數值,α0為平均值,α1、β1為年周期振幅,α2、β2為半年周期振幅。利用式(7)可得到基于GPT3模型的各類氣象參數,GPT3-PWV與GNSS-PWV計算原理相同,均可利用式(6)計算得到。
1.4 精度統計方法
采用偏差bias和均方根誤差RMSE作為精度評定標準:
(8)
(9)
式中,Xmodel,i、Xreal,i分別為PWV的模型值和參考值,n為樣本數。
2 PWV精度分析
2.1 GPT3-PWV
根據GNSS-PWV計算原理和GPT3模型提供的氣象參數,可在無氣象參數情況下獲取PWV。由于篇幅所限,本文只列舉安慶、阜陽及杭州站GPT3-PWV及其bias(圖1)。由圖可知,GPT3-PWV與探空PWV變化趨勢基本一致,呈周期性變化,春冬季精度優于夏季精度。這是由于長三角地區主要為亞熱帶季風氣候,雨熱同期,春冬季空氣中的水汽含量遠低于夏季。
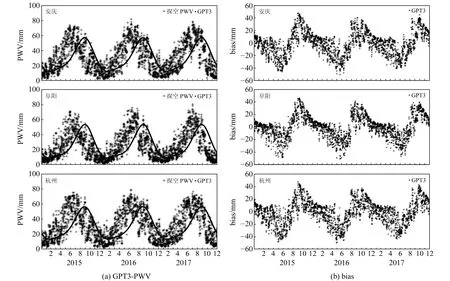
圖1 2015~2017年安慶、阜陽、杭州站GPT3-PWV及其bias
表2為2015~2017年7個探空站獲取的GPT3-PWV精度統計(單位mm)。由表可知,平均bias和RMSE分別為0.57 mm和9.15 mm,未達到理想精度。這是由于GPT3模型獲取的平滑氣象參數會丟失實時氣象參數的細節信息,缺乏時效性,且與實測數據存在較大差異。而采用Askne-Nordius模型計算的GPT3-ZWD涉及到e、Tm等參數,與P、T和高程均有很強的相關性,多種氣象誤差累積和交叉影響,造成ZWD精度下降,從而導致由GPT3模型反演的PWV精度較低,僅可作為無實測氣象參數時的參考。

表2 2015~2017年7個探空站GPT3-PWV精度統計
2.2 地面氣象資料法
圖2為基于地面氣象資料法計算的2015~2017年部分探空站的PWV及其偏差。由于篇幅所限,本文僅列出安慶、阜陽和杭州站。由圖可知,地面測得的露點資料能很好地反映空氣中的水汽狀況。此外,地面法獲取的PWV呈季節性變化,冬季精度明顯優于夏季精度,且基于地面法1推算的PWV值比地面法2推算的PWV值大,更接近于真實值,尤其是在夏季。

圖2 2015~2017年地面法PWV及其bias
表3為基于兩種地面法獲取的PWV精度統計(單位mm)。基于地面法1獲取的PWV平均bias和RMSE分別為0.22 mm和8.00 mm,基于地面法2獲取的PWV平均bias和RMSE分別為-0.51 mm和8.34 mm。總體而言,地面法1的精度稍優于地面法2,雖然地面法1與地面法2均是利用氣象資料建立的經驗公式,但地面法1考慮了露點溫度、緯度和高程,而地面法2僅考慮了地面水汽壓。由于地面露點資料僅能反映地面附近的濕度狀況,由此得到的經驗關系式仍存在20%的誤差[7]。與GPT3-PWV相比,兩種地面法計算的PWV精度略有提升,但仍未達到理想水平。
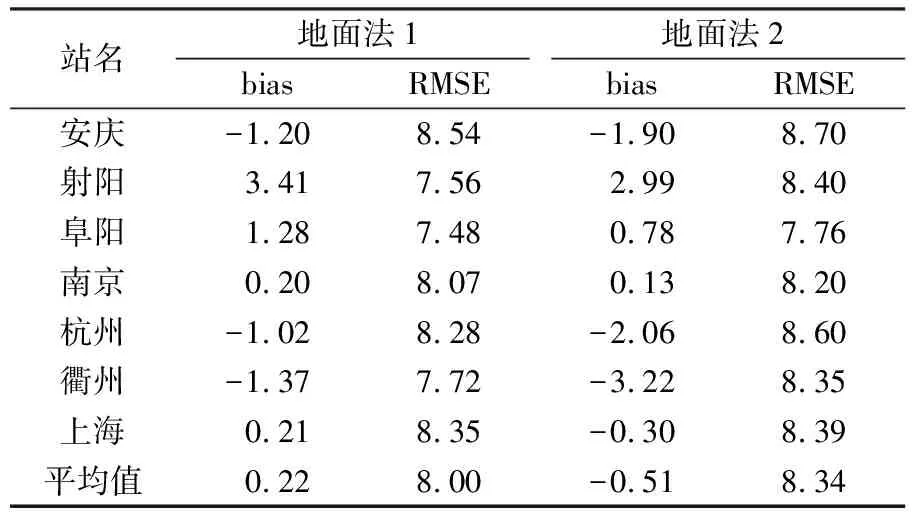
表3 2015~2017年基于地面法的PWV精度統計
2.3 GNSS-PWV
圖3、圖4分別為安慶站和射陽站2017年GNSS-PWV及其bias,表4為兩站2017年GNSS-PWV的精度統計(單位mm)。由圖可知,GNSS-PWV與探空PWV在2017年的差值基本保持在10 mm以內,且冬季偏差小于夏季偏差。由表4可知,GNSS-PWV的平均bias和RMSE分別為0.05 mm和3.50 mm,與探空PWV具有較好的一致性。
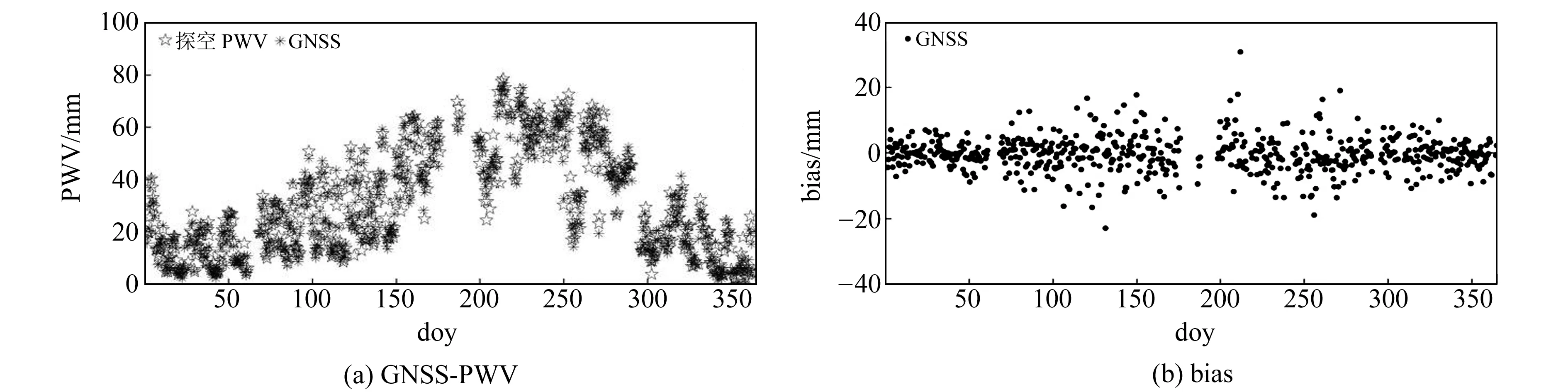
圖3 2017年安慶站GNSS-PWV及其bias
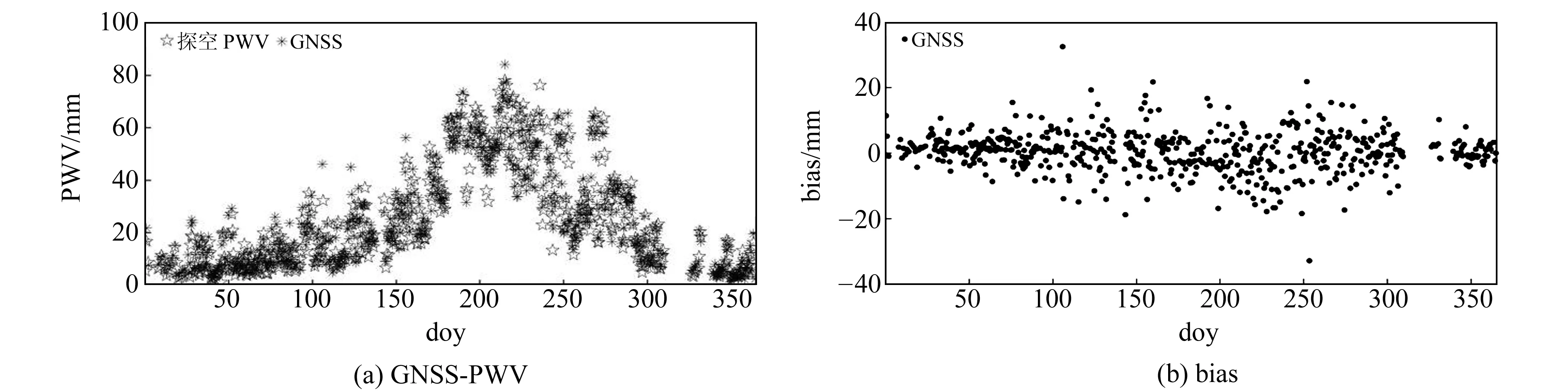
圖4 2017年射陽站GNSS-PWV及其bias
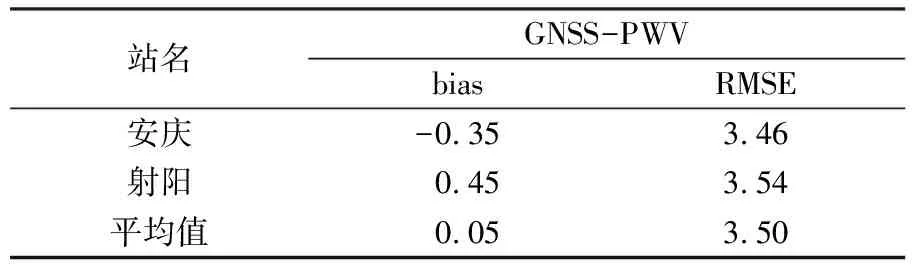
表4 2017年安慶站和射陽站GNSS-PWV精度統計
總體而言,GNSS-PWV精度最高,不受天氣狀況影響且儀器長期穩定無需標定,具有廣闊的應用前景;地面法PWV精度較低,但計算簡單、可實時獲取結果,在無法實時處理GNSS數據以及缺乏GNSS站的情況下具有很強的實用價值。但上述兩種方法均需要探空站或GNSS站的觀測數據,在很多無法獲取氣象參數的地區具有較大的局限性,因此可利用GPT3模型在精度要求較低的地區獲取實時PWV。
3 結 語
1)從精度上看,GNSS-PWV精度最高,地面氣象資料法次之,GPT3-PWV精度最低。其中,地面氣象資料法1的精度優于地面氣象資料法2,4種方法獲取的PWV均呈現出季節特性,冬季精度優于夏季精度。
2)從時效性和數據依賴程度上看,GPT3模型無需任何氣象參數,可實時獲取PWV;地面法需要露點溫度、緯度和高程等參數;GNSS-PWV同時需要GNSS數據和實測氣象數據。
3)在同時擁有氣象資料和GNSS數據的情況下,可基于GNSS獲得精度最高的GNSS-PWV;在僅有地面氣象資料而缺乏GNSS數據時,可利用地面露點資料得到實時PWV;若GNSS數據和氣象數據均缺失,則可利用GPT3模型計算PWV。

