矩形巷道錨桿中性點位置特征研究*

任何，宋義敏，張軍徽

(北方工業大學 土木工程學院，北京 100144)

0 前言

隨著礦山開采向深部發展，地應力呈非線性增加。開采時軟弱煤層在高地應力作用下容易發生失穩破壞，對采礦工程造成極大的危害[1-3]。因此，開展巷道支護研究具有十分重要的意義。

近年來，巷道支護已經成為煤礦開采領域的熱點[4-10]。其中，錨桿及錨索等支護結構廣泛應用于各種巖土工程中[11-14]，國內外學者們為此開展了大量的研究工作。程良奎等[13]根據模型試驗和現場試驗,對摩擦式錨桿的作用原理進行了探討，揭示了摩擦式錨桿的支護效果和先柔后剛的特點；楊慶等[14]等根據局部變形理論，推導出全長注漿巖石錨桿的界面剪應力和軸向載荷的分布函數；李桂臣等[15]采用彈塑性力學理論，推導出注漿前后錨固劑與孔壁之間剪應力分布的理論解析式；王正義等[16]將沖擊應力波進行合理簡化，建立了平面P波與圓形錨固巷道相互作用簡化模型；宋洋等[17]在局部變形理論基礎上，對全長黏結型錨桿錨漿界面破壞類型的錨固機理進行了分析研究；LI等[18]建立了三種錨桿的分析模型，指出現場錨桿具有拾取長度、錨固長度和中性點；姚顯春等[19]以中性點的軸力為集中力，由半無限體受集中力作用的Mindlin解導出中性點以內錨桿界面剪應力的分布規律；朱訓國等[20]結合中性點理論，對影響中性點位置的因素進行了分析，得出了影響錨桿中性點位置的相關因素。雖然學者們在錨桿及錨索等支護結構的研究方面取得了很多有意義的成果，但大多數研究都是針對同性巖體、圓形洞室，沒有考慮層狀結構的影響，因此，本文以全摩擦錨桿為例，通過理論分析對矩形巷道層狀圍巖中的錨桿應力分布特征進行探究。

本文通過將煤層頂板簡化為只發生剪切變形的剪切梁模型，對開挖后煤層的橫向變形進行分析；進而以煤層的橫向變形為參量，結合錨桿已有的本構解析解，建立矩形巷道錨桿應力計算模型，對其中性點位置特征進行分析。

1 錨桿應力計算模型

圖1為嵌入煤層的錨桿，錨桿承受的剪應力應該分為兩部分。首先，巷道開挖后，煤層巖體向采空區發生變形，錨桿對巖體變形產生約束作用。即煤層巖體橫向變形對錨桿產生了剪應力τ1。而隨著煤層變形向深部遞減，作用在錨桿上的剪應力τ1逐漸減小，即錨桿巷道端的部分對深部的部分產生拉拔作用，引發了煤層巖體施加給錨桿的另一個剪應力τ2來抑制這種拉拔趨勢。

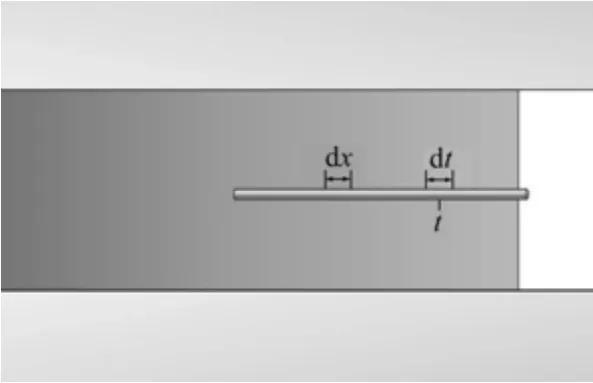
圖1 煤層中的錨桿

在嵌入錨桿的煤層取單元體b如圖2所示，假設原始應力條件下煤層巖體橫向變形為du，而設置 錨桿后，圍巖的應力分布重新調整，煤層巖體的實際變形變為dub；變形的減小量dur則是由錨桿與煤層巖體間相互作用，使得煤層巖體中應力增加了Δσr的結果。

圖2 煤體單元

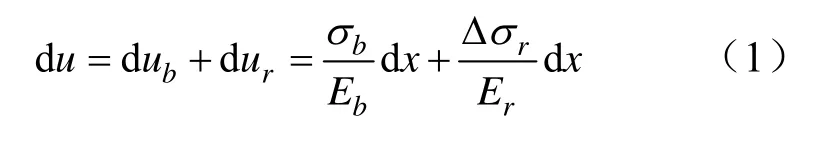
dx左端界面平衡方程為：

式中，S為錨桿影響范圍，A為錨桿截面面積。

將式（2）代入式（1），得到錨桿軸應力與煤層巖體變形關系式：

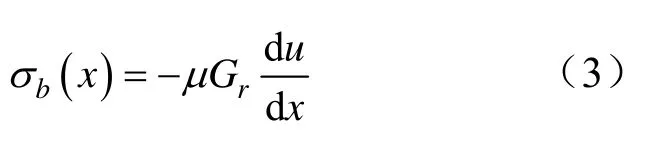
錨桿單元平衡方程為：

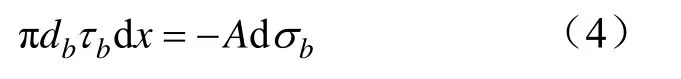
即：

式中，db為錨桿截面直徑。

則原始應力條件下的煤層巖體變形引發的剪應力τ1為：

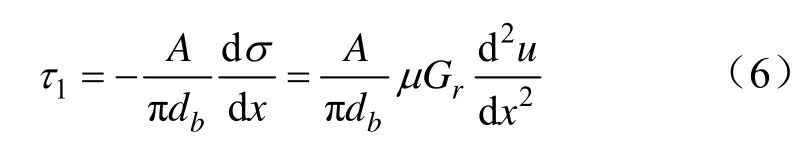
根據I W FARMER拉拔作用下錨桿剪應力衰減公式，將其應用于錨桿可得到：

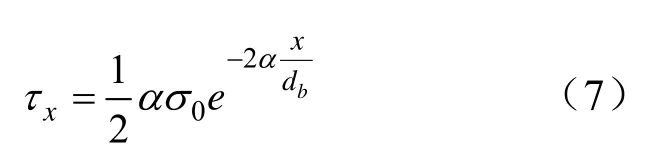
煤層巖體變形引發的剪應力τ1導致了錨桿內部dt處軸應力的差值dσ，dσ在x處引發了接觸面施加給煤層巖體的剪應力τ2。則dt處軸應力在x處引發的剪應力為：

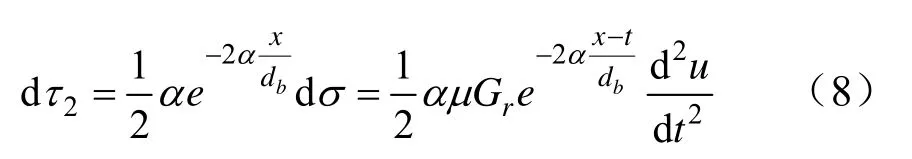
則x處的τ2為：

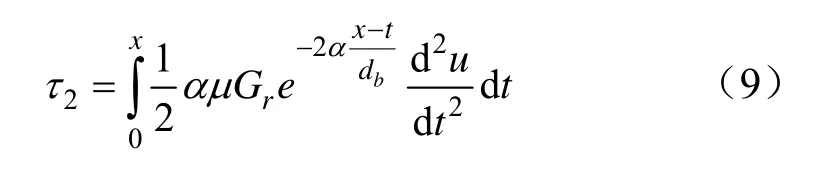
所以，煤層巖體中錨桿剪應力計算公式為：

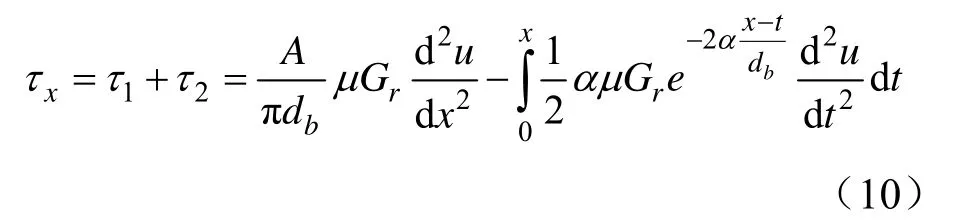
2 剪切梁模型

將煤層上頂板簡化為只考慮剪切變形的剪切梁，假設煤層巖體為均勻、各向同性，底板為剛性，忽略其變形，進而建立剪切梁模型，對采空后煤層峰前階段的橫向變形進行分析。計算模型如圖3所示，其中，頂板厚度為H，煤層厚度為h。

圖3 煤層變形計算

取頂板單元體如圖4所示，定義頂板垂向撓度為ω，橫截面剪力為Q，平均剪應力為τ，平均剪應變為γ，而上覆巖層對頂板的壓力為q，煤層對頂板的支撐應力為p，剪切梁剪切模量為K。

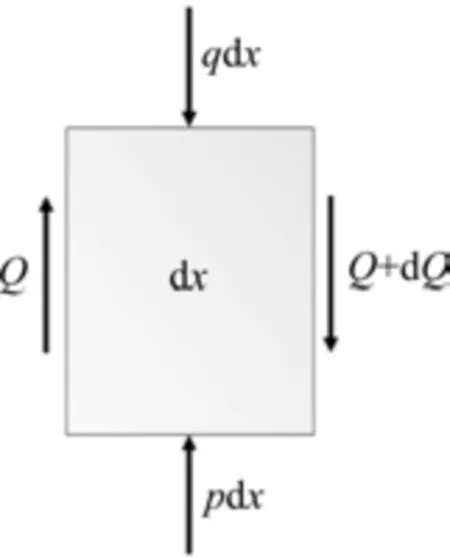
圖4 頂板單元體

豎向平衡公式為：

幾何方程有：

物理方程有：

聯立式（11）至（15）得：

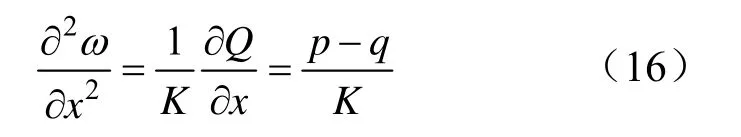
取煤層單元體如圖5所示，煤層與頂板間摩擦力為τf，有平衡方程：

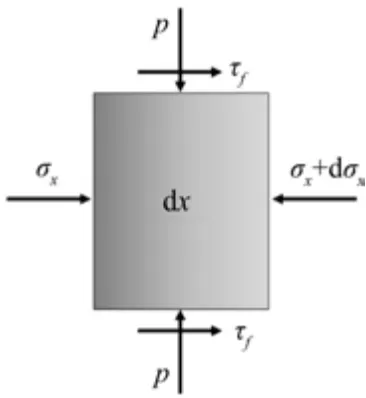
圖5 煤層單元體

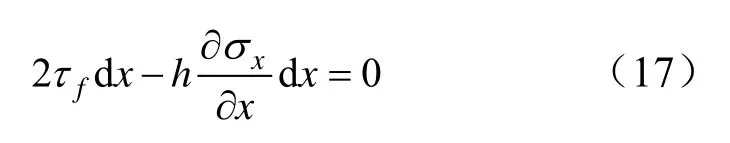
簡化得：

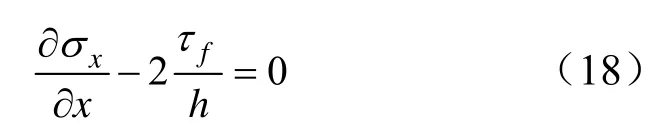
采空后，煤層發生彈性變形，其中，在工作面附近出現彈性變形外區，此時煤層與頂板發生相對滑動，產生橫向變形。而在遠離工作面的區域為彈性變形外區，煤層與頂板間無相對滑動。采空區長度為a，彈性變形外區長度為B=b-a，如圖6所示。

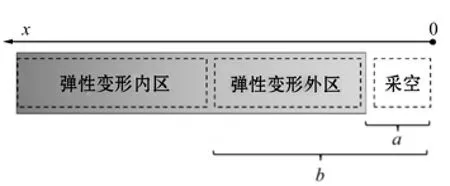
圖6 煤層變形區域分布

在彈性變形內區，即b≤x，有公式：

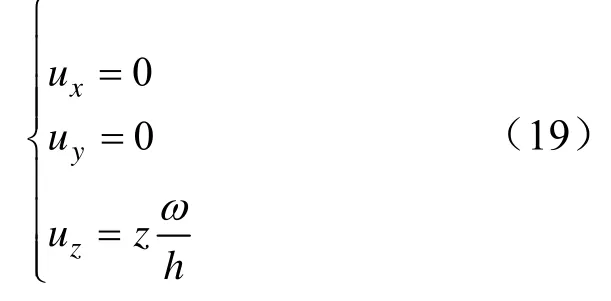
代入平面應變公式得到彈性變形內區基本方程：

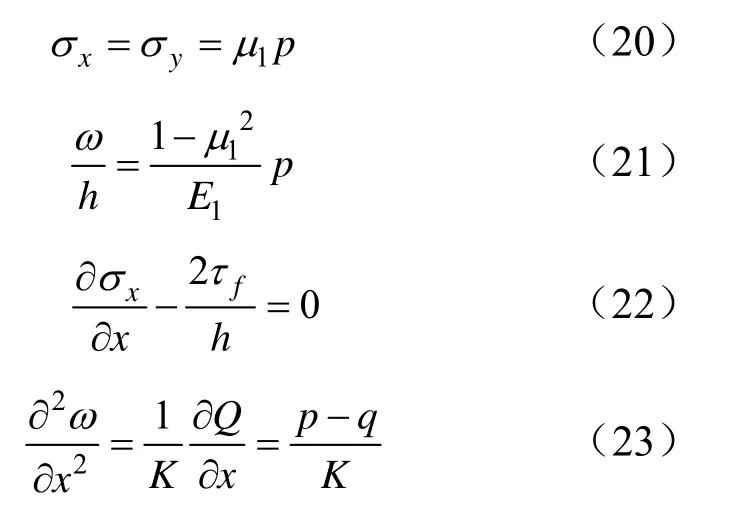
聯立式（20）至式（23）得：

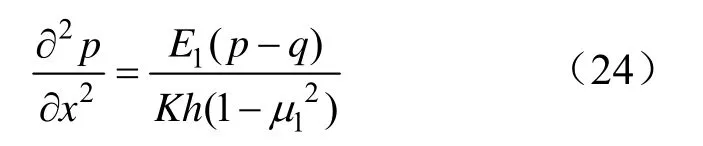
在彈性變形外區，即a≤x≤b，有公式：

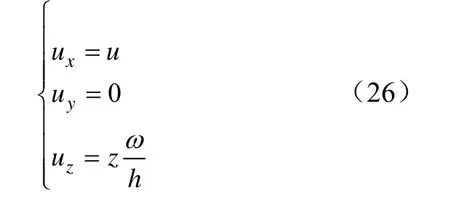
將式（26）代入平面應變公式得到彈性變形內區基本方程：

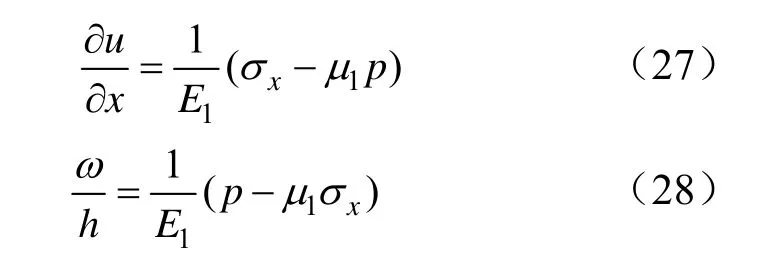
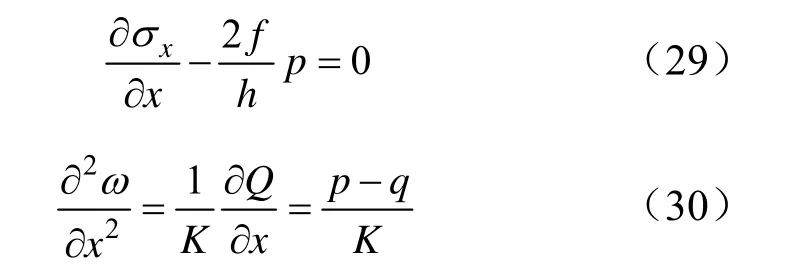
聯立式（27）至式（30），得到：

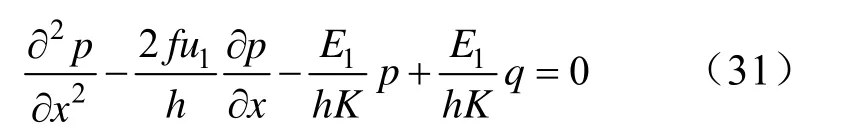
解得弱夾層彈性變形外區橫向變形u2：

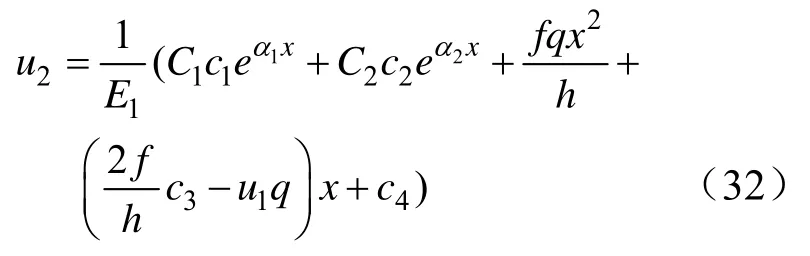
3 中性點位置影響因素分析

下面對巖體及錨桿力學參數取值，分析不同因素對錨桿中性點位置的影響。錨桿直徑db=35 mm，長度為1.5 m，楊氏模量E=210 GPa，影響范圍直徑d0=200 mm。煤層巖體楊氏模量為5 GPa（3 GPa、4 GPa、6 GPa），泊松比v=0.35，橫向應力系數為υ=0.54（0.33，0.43，0.67），厚度h=3 m，接觸面摩擦系數f=0.5。頂板剪切模量為8 GPa，厚度H=5 m，上覆巖層壓力q=10 MPa。假設采空區長度a=4 m，彈性變形外區長度b=5.58 m。

3.1 煤層彈性模量的影響

圖7為煤巖不同彈性模量時錨桿的應力分布。如圖7所示，當煤巖彈性模量為3 GPa時，中性點在0.66 m處出現，軸應力峰值為15.5 MPa；當煤巖彈性模量為4 GPa時，中性點在0.56 m處出現，軸應力為12.0 MPa；當煤巖彈性模量為5 GPa時，中性點在0.49 m處出現，軸應力為9.9 MPa；當煤巖彈性模量為6 GPa時，中性點在0.44 m處出現，軸應力為8.4 MPa。由此可見，當煤巖彈性模量增加時，錨桿中性點到洞壁的距離減小，軸力峰值減小。

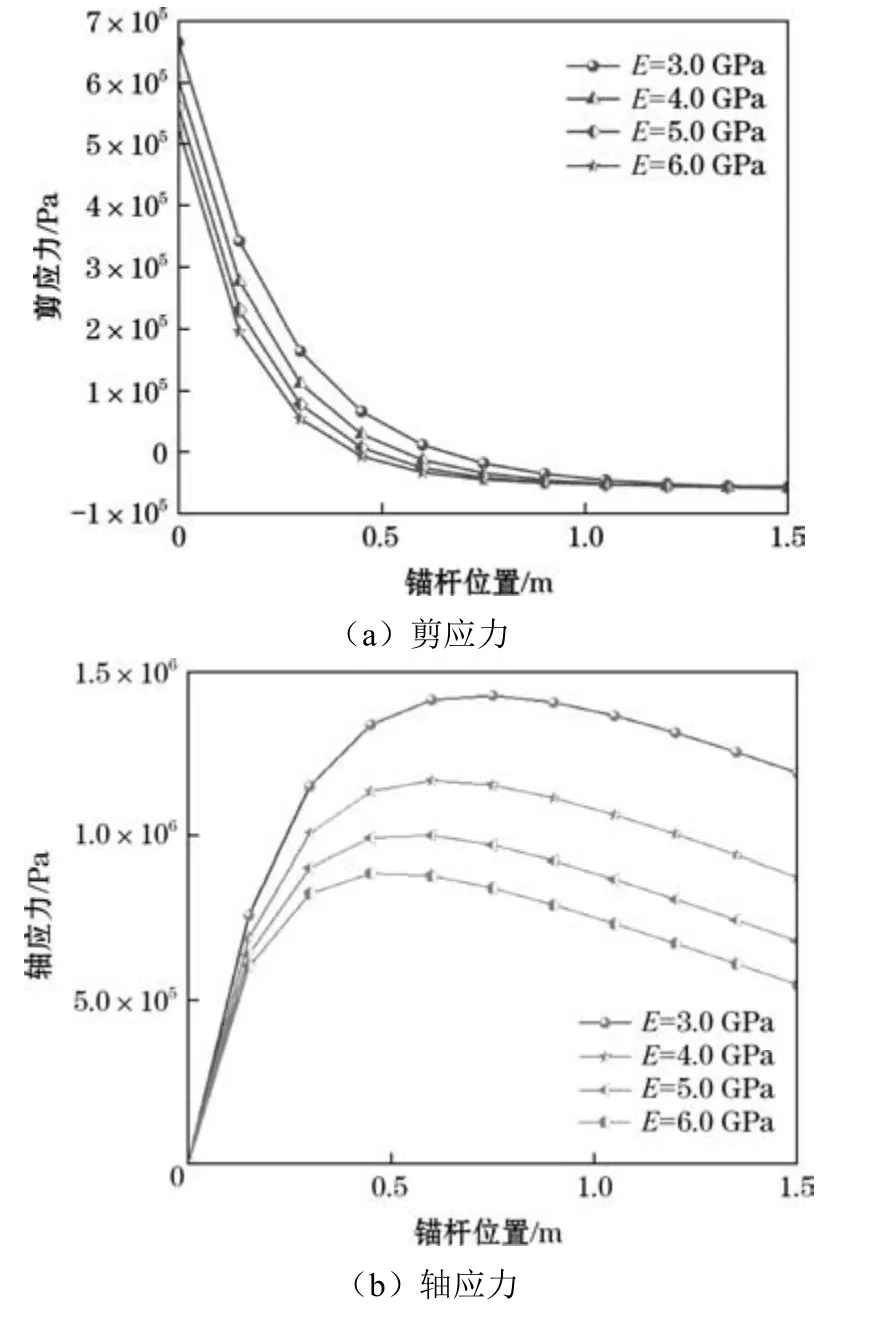
圖7 煤巖不同彈性模量時錨桿的應力分布

3.2 不同橫向應力系數的影響

圖8為煤巖不同橫向應力系數時錨桿的應力分布圖。如圖8所示，當煤巖橫向應力系數為0.33時，中性點在0.46 m處出現，軸應力峰值為13.3 MPa；當煤巖橫向應力系數為0.43時，中性點在0.47 m處出現，軸應力為11.8 MPa；煤巖橫向應力系數為0.54時，中性點在0.49 m處出現，軸應力為9.9 MPa；煤巖橫向應力系數為0.67時，中性點在0.51 m處出現，軸應力為7.6 MPa。由此可見，當煤巖橫向應力系數增加時，錨桿中性點到洞壁的距離增大，軸力峰值減小。

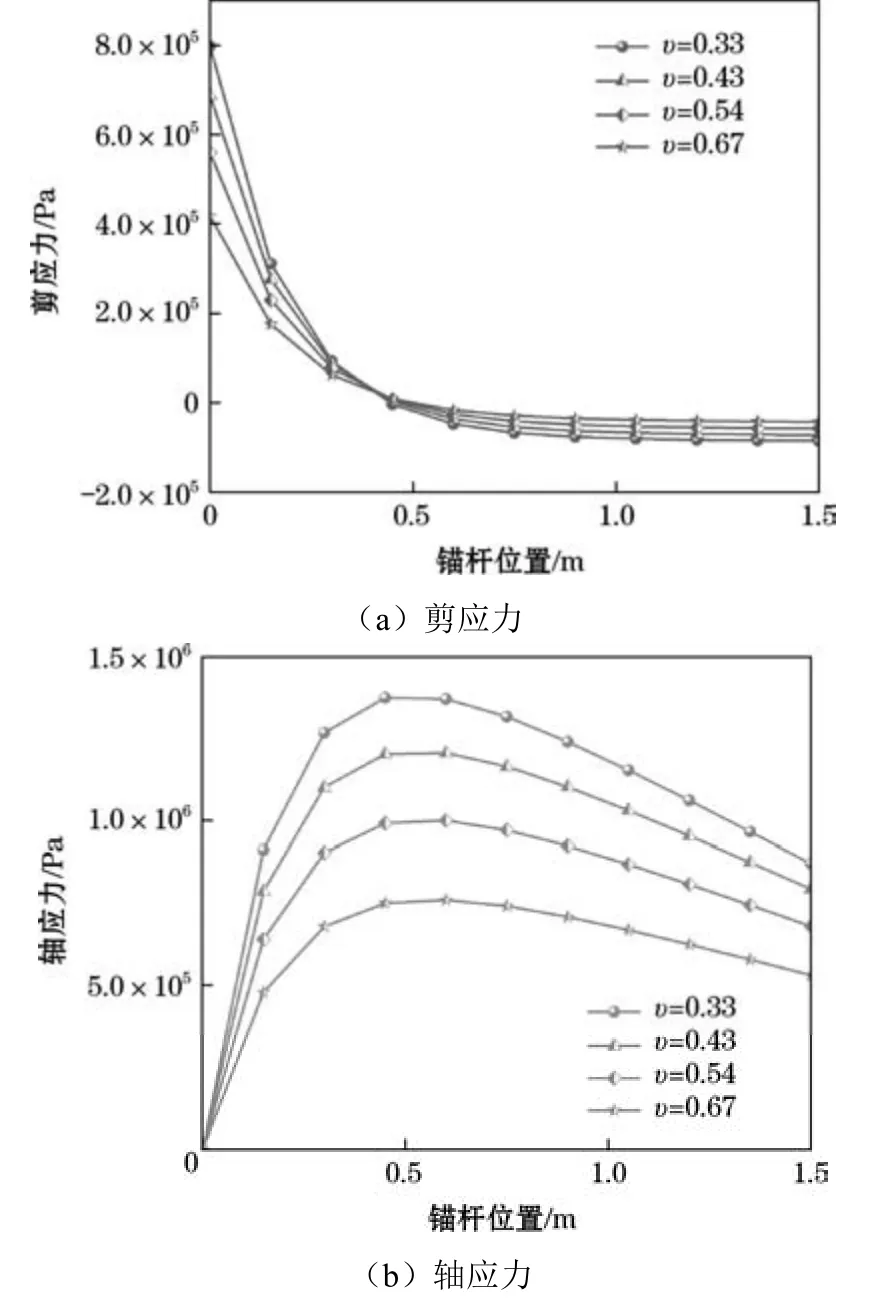
圖8 煤巖不同橫向應力系數時錨桿的應力分布

4 結論

（1）錨桿在矩形巷道煤層中的應力分布也符合中性點理論的假設，剪力沿錨桿先減小，后改變方向增大，軸力先增大后減小；在中性點位置，剪力為零，軸力達到峰值。

（2）當煤巖彈性模量增加時，錨桿中性點到洞壁的距離減小，軸力峰值減小；當煤巖橫向應力系數增加時，錨桿中性點到洞壁的距離增大，軸力峰值減小。