新型變剛度滑移支座在網殼中的隔震性能研究

賀擁軍，程雅，周緒紅

（1.湖南大學土木工程學院，湖南長沙 410082；2.重慶大學土木工程學院，重慶 400044）

大跨空間結構作為公共類建筑的主要形式得到日益廣泛的應用，研究并提高其隔震性能具有重要的現實意義［1］.滑移隔震支座可以將上部結構和下部運動分離，通過相對滑動和摩擦耗能有效限制地震能量向上傳遞［2］.針對其在地震中支座位移過大和難以自復位的問題，已有許多學者提出并深入研究了各種具有恢復機構的隔震支座.1987 年Zayas等［3］提出了摩擦擺支座（FPB）對滑動隔震系統作出改進，該支座滑動面為圓弧狀，滑動過程中可利用重力復位.隨后科研人員對FPB 進行了大量的試驗和理論分析證明其有效性［4-6］，薛素鐸等［7］進行了應用FPB的單層球面網殼結構抗震性能分析，孔德文等［8］研究了三維地震作用下FPB 參數對網殼結構抗震性能影響.由于FPB滑動剛度恒定不變，遭受強烈的長周期地震（如近斷層地震）時，可能會出現共振問題［9］，各國研究人員提出了多種類型的變曲率摩擦擺支座，通過變化的滑動面曲率實現剛度隨位移變化［10-14］.Shaikhzadeh 等［15］對幾種常見的變曲率支座進行數值模擬，驗證了其在近斷層地震下良好的隔震性能.

基于以上研究，本文提出一種變剛度滑移支座（Nonlinear Spring-Friction Bearing，NFB），由摩擦滑移系統和非線性圓錐彈簧組成，相對于變曲率摩擦擺制造更為簡單.對于大跨空間結構，隔震支座通常設置于屋蓋和下部支承結構之間，允許的支座變形空間有限，NFB 可以在提供良好的隔震效果的同時減小支座位移峰值和殘余位移.本文對NFB 的構造和理論模型作了詳細的介紹，建立精細化實體模型，通過數值模擬分析其滯回性能，最后將NFB 應用于單層球面網殼，考察其隔震效果.

1 構造和工作原理

變剛度滑移支座（NFB）的構造如圖1、圖2 所示.NFB主要由滑動摩擦支座和圓錐彈簧復合組成，其組件分別為：頂板，與上部結構相連；蓋板，上與頂板以螺栓相接，下與滑塊自然接觸，接觸面為球形，可使支座適應多向轉動自由度；環形抗拔擋板，焊接于支座側壁上，并在內側及上下表面設置防撞層，防撞層由橡膠和鋼板組成；滑塊，傳遞上部結構荷載同時可在水平方向自由滑動；聚四氟乙烯板，內嵌在滑塊底面，地震作用下通過滑動摩擦耗能，相比于鋪設在底板表面，可避免摩擦材料在較大壓力下變形凹陷影響滑動的情況；支座側壁，限制滑塊最大位移；圓錐彈簧，均勻布置在滑塊周圍連接滑塊與支座側壁，起到復位作用，同時由于其構造特點，可從自然長度完全壓平至簧絲厚度，節省了支座空間，且荷載和變形是非線性的關系，可防止共振現象發生，受壓時剛度隨位移增大而增加，在遭遇高強度或脈沖型地震時更利于減小支座位移以及防止滑塊對支座側壁的過大沖撞；底板，與下部結構相連.

將NFB應用于建筑物中，當受到地震作用時，支座滑塊和底板發生相對滑動，通過滑動摩擦耗能，同時彈簧發生變形提供彈性恢復力，當支座位移超過線形臨界值后，支座剛度隨位移增大，可以提供更大的恢復力.

2 理論分析

NFB中滑動系統提供的摩擦力Ff可表示為：

式中：μ為滑動摩擦系數；W為作用于滑動面的法向荷載；為支座水平滑動速度；sgn（）為符號函數.

圓錐形螺旋彈簧相對于圓柱形螺旋彈簧，具有較大的穩定性，可以通過適當設計圓錐彈簧的各項參數來實現隔震系統所需的非線性行為.具有均勻節距的圓錐形彈簧如圖3 所示，當（R2-R1）≥N·d時，彈簧可壓縮至一個線徑厚度.錐形彈簧沿其長度具有線性增加的環直徑，從而使每個環之間具有不同的剛度，當所受負載未使彈簧圈開始接觸前，負載與變形關系是線性的，如果外力繼續增加，則彈簧從大圈開始接觸，因此彈簧的有效圈數隨著負載的增加而減少，從而導致剛度逐漸增加.在兩次連續的彈簧圈接觸發生之間，剛度保持不變，因此，本文彈簧模型的載荷變形曲線采用多線性模式.

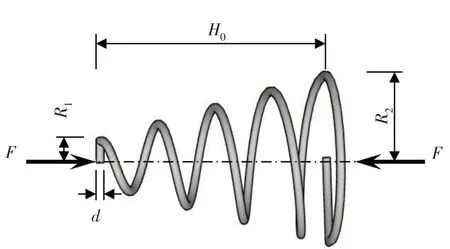
圖3 圓錐彈簧Fig.3 Conical spring

在軸向載荷下（如圖3 所示），彈簧的簧絲橫截面受到剪切和扭轉的共同作用.對于橫截面較薄的彈簧，剪切變形通常可以忽略不計，因此彈簧中的大部分應變能都來自扭轉應力，還沒發生環接觸的彈簧應變能U可以表示為：

式中：T表示扭轉力；G表示剪切模量；J表示金屬簧絲截面極慣性矩；L0表示簧絲總長度.

外力做功等于彈簧增加的應變能，從而彈簧變形δ可表示為：

式中：F表示彈簧所受軸力；r表示彈簧環半徑；θ表示從彈簧最小端開始到半徑r處轉過的角度；N表示有效環的總數.環半徑沿彈簧絲均勻變化，可表示為：

式中：R1表示最小環的半徑；R2表示有效環中最大環的半徑.代入式（3）可得：

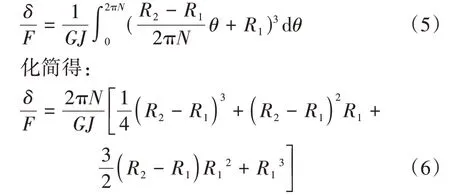
其中J=πd4∕32，d為線徑（即金屬彈簧絲直徑），代入上式得圓錐彈簧剛度為：

當彈簧受拉時，N不變，R2不變，從而剛度表現為線性；當受壓時，隨著變形增大有效環數N減少，R2減小，從而剛度表現出非線性.

NFB 水平向總控制力等于摩擦力和彈簧合力之和：

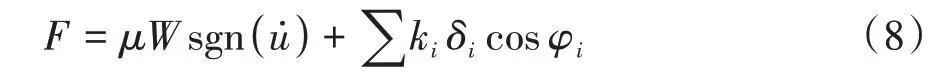
式中：δi表示第i根彈簧變形；ki表示第i根彈簧變形量為δi時的剛度；φi表示第i根彈簧與滑塊運動方向的夾角.

3 變剛度滑移支座的數值模擬

為分析變剛度滑移支座（NFB）在低周往復荷載下的滯回響應和應力分布狀態，以及彈簧參數對支座性能的影響，采用通用有限元軟件ABAQUS 進行數值模擬.

3.1 ABAQUS模型的建立

支座設計位移為120 mm，滑塊滑動面（聚四氟乙烯板）直徑為370 mm.頂板、底板、滑塊、側壁均為鋼材制成，摩擦材料為聚四氟乙烯（PTFE）.由于支座整體宜控制在彈性狀態，鋼材和聚四氟乙烯（PTFE）的本構模型均采用各向同性彈性模型［16］，鋼材的彈性模量E=2.1×105N∕mm2，泊松比υ=0.3；聚四氟乙烯的彈性模量E=280 N∕mm2，泊松比υ=0.42，設計強度為30 N∕mm2.整體模型采用8 節點六面體線性減縮積分單元（C3D8R）進行模擬.假設滑塊的聚四氟乙烯滑動面和底板的不銹鋼滑動面之間接觸屬性中的法向作用采用“硬接觸”，切向摩擦力遵循庫侖定律，滑動摩擦系數為0.05.

彈簧材料為鋼材，剪切模量取G=8×104N∕mm2，圓錐彈簧（編號N-1）幾何參數取值為：最小圈半徑R1=20 mm，最大圈半徑R2=40 mm，自然高度H0=120 mm，總有效圈數N=4，線徑d=5 mm.根據式（6）和式（7）可知圓錐彈簧的線性段位移和剛度變化與各項幾何參數相關，在N-1 的基礎上改變線徑d得到部分荷載-變形關系如圖4（a）所示，在N-1 的基礎上改變總有效圈數N值得到部分荷載-變形關系如圖4（b）所示，圖4 中位移為受壓變形，受拉時剛度等于受壓初始剛度.采用軸向連接器單元對其進行模擬，單元參數取自圖4，在滑塊周圍均勻布置8 根相同的圓錐彈簧.另外將圓錐彈簧（N-1）換成初始剛度與之相同的普通彈簧（L-1），形成定剛度滑移支座，與NFB的性能進行對比分析.

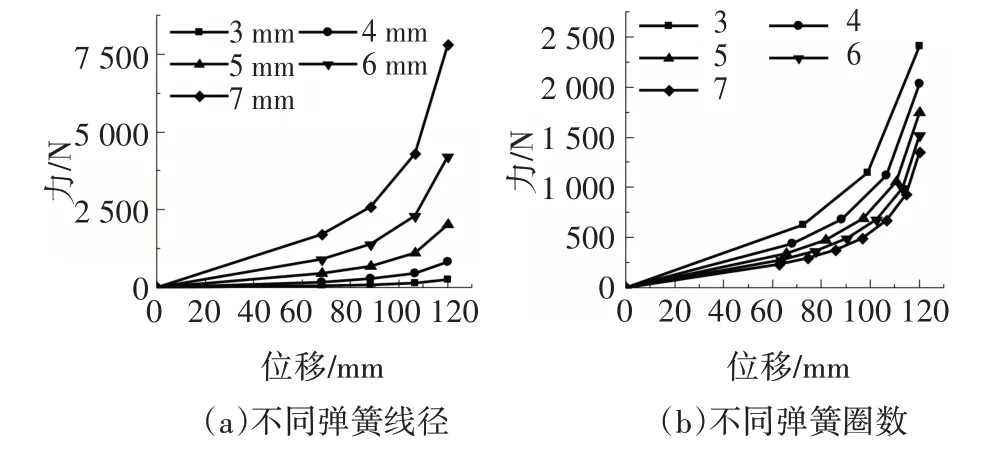
圖4 圓錐彈簧荷載-變形圖Fig.4 Load-deformation diagram of Conical spring

整個模擬過程設置3 個分析步：施加極小的預加荷載使各個接觸面發生接觸—施加正式豎向恒荷載—保持豎向恒載施加水平向簡諧位移激勵.豎向恒載為W=100 kN，水平簡諧位移為S=Asin（2πωt），其中A為振幅取120 mm，ω為頻率取0.5 Hz.

3.2 模擬結果分析

3.2.1 滯回特性

基于NFB的理論模型編制了MATLAB程序來描述其滯回響應，并繪制其理論分析滯回曲線.圖5 所示為使用上述N-1 圓錐彈簧時理論分析和ABAQUS數值模擬分析所得的滯回曲線對比圖，可以看到模擬結果與理論分析基本吻合，滯回曲線對稱飽滿，具有良好的滯回耗能能力.

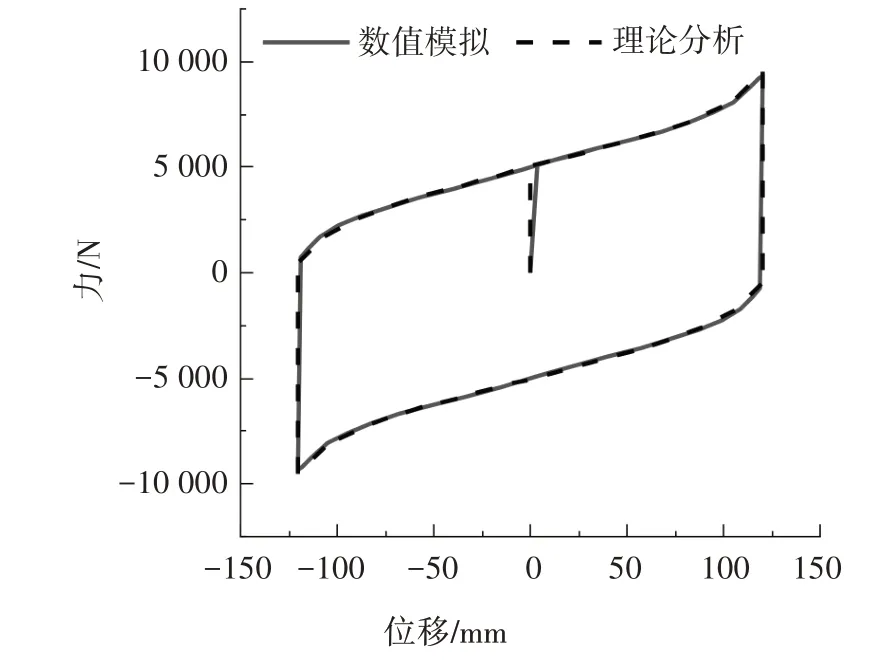
圖5 NFB試件滯回曲線Fig.5 Hysteretic curve of NFB specimen

圖6 所示為使用非線性圓錐彈簧和普通彈簧的兩種滑移支座滯回曲線對比圖，兩類支座滯回環面積相等，具有相同的耗能能力，這是因為彈簧僅提供回復力，支座通過滑動摩擦耗散能量.圖6 中兩種支座滯回曲線初始剛度相等，NFB 線性段位移臨界值為68 mm，當支座位移小于該臨界值時剛度保持不變，當位移大于臨界值時剛度隨位移增大而增大.NFB 的剛度變化特點使得其在地震作用較小時滯回特性與普通定剛度滑移支座相同，在地震作用較大時可提供更大的恢復力，防止位移過大，并且減小殘余位移.

圖6 兩種滑移支座對比Fig.6 Comparison of two sliding bearings

圖7 展示了圓錐彈簧參數對NFB 的滯回曲線的影響.圖7（a）為在N-1 基礎上取4 種不同彈簧線徑時的滯回曲線，結果顯示各滯回曲線的線性段位移臨界值基本相等，線徑d越大初始剛度和非線性剛度越大.圖7（b）為在N-1 基礎上取4 種不同彈簧有效圈數時的滯回曲線，結果顯示彈簧有效圈數N越大，支座的線性段位移臨界值越小，整體剛度也越小，但對剛度的影響并不十分顯著.通過參數分析可知變剛度隔震支座滯回特性變化規律，從而可以改變支座參數以適應不同結構不同場所的隔震需求.

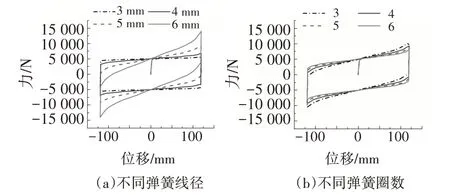
圖7 圓錐彈簧參數對NFB滯回影響Fig.7 Influence of conical spring parameters on NFB hysteresis

3.2.2 應力分析

通過觀察變剛度滑移支座工作狀態中的應力分布情況，可以發現薄弱部位并針對性地改善，圖8 所示為NFB 試件在設計位移處的應力云圖.在分析過程中支座均處于彈性范圍內，從圖8 可以看到該時刻最大應力值為20.45 N∕mm2，出現在頂板和蓋板相接處，因為此時支座位移最大，所受剪力最大，而頂板與蓋板相接處水平投影面積最小，故應力最大.當支座應用中受到更大的豎向荷載時，需要適當加強此處.另外值得注意的是，支座位移越大，彈簧與支座側壁連接處應力集中越明顯，若使用線徑更大的彈簧，需注意增加支座側壁厚度.

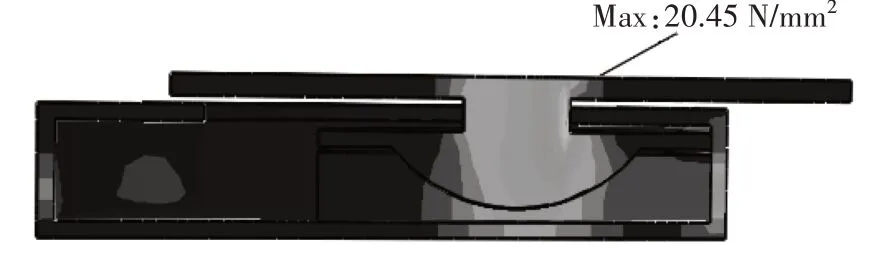
圖8 NFB在設計位移處的應力云圖Fig.8 Stress nephogram at the design displacement of NFB

4 單層球面網殼結構模型

4.1 結構體系

本文選用K8 型單層球面網殼作為研究對象驗證NFB 的隔震性能，網殼結構參數見表1，屋蓋桿件均為圓形鋼管，采用Q235B 鋼材，節點均采用剛性連接，屋面荷載取1.5 kN∕m2，結構整體構造如圖9所示.

表1 網殼結構參數Tab.1 Parameters of the reticulated shell structure

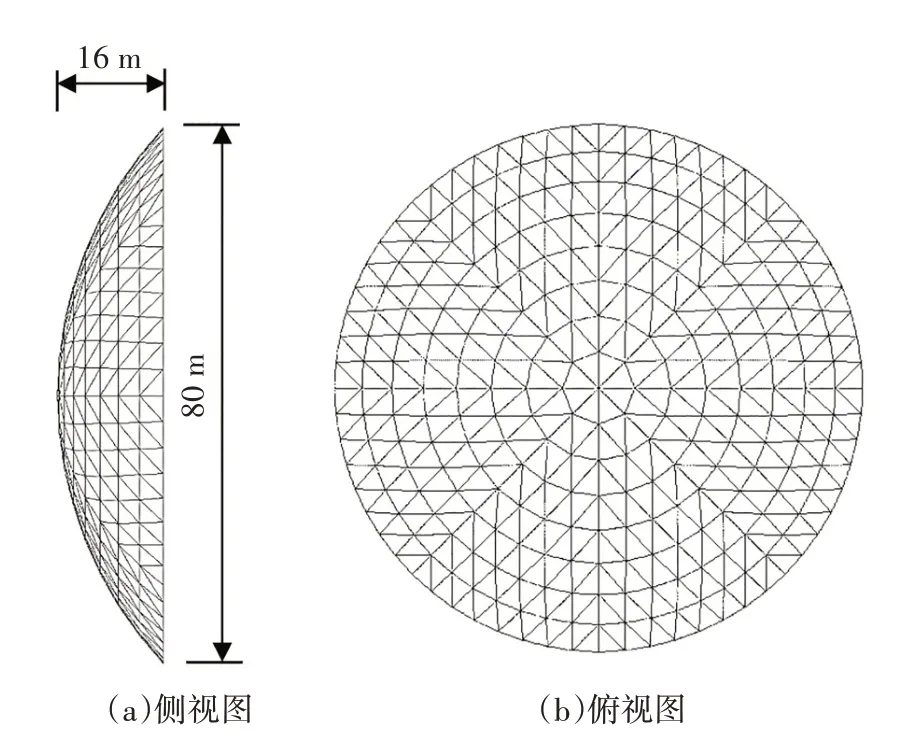
圖9 K8型單層球面網殼結構Fig.9 K8 single-layer spherical reticulated shell structure

為評估NFB 對網殼結構的隔震效果，共設置3組網殼結構模型：①布置固定鉸支座；②布置NFB；③布置與NFB 初始剛度相同的定剛度滑移支座.每一類支座均滿布于網殼最外環節點下，共64 個，其中NFB參數如表2所示，支座限位移為150 mm.

表2 變剛度滑移支座參數Tab.2 Parameters of NFB

4.2 結構有限元分析

運用有限元軟件ANSYS 建立整體結構的有限元模型，桿件建模采用BEAM188 單元，材料彈性模量E=2.06×105MPa，泊松比υ=0.3，本構關系定義為雙線性隨動硬化模型（BKIN），屈服準則為Mises 極限屈服準則，強化準則為隨動強化準則.在網殼節點間建立表面效應單元SURF154，約束所有節點，施加屋面荷載求得節點反力再除以重力加速度得到節點等效質量，用質量單元MASS21 來模擬.NFB 的摩擦滑移采用接觸單元CONTA178 來模擬，非線性圓錐彈簧用COMBIN39 來模擬，支座一端與最外環節點相連一端接地.

對3 組模型進行動力時程分析，并考慮結構在重力荷載下的初始內力及變形.選用El-Centro 波進行3 向加載，地震動強度為400 cm∕s2，X、Y、Z3 個方向的加速度比值滿足1∶0.85∶0.65.

4.3 結構地震響應

提取網殼結構所有桿件、節點和支座的地震響應峰值的最大值，結果見表3 和表4，表中相對位移指相對于最外環節點的位移，桿件應力未包含最外環桿［7］.

根據表3 的結果可知，相對于鉸支座結構，變剛度滑移支座（NFB）和定剛度滑移支座結構的各項地震響應指標都有明顯減弱：兩種支座對桿件最大應力減小量相同，均為45%左右；對節點最大加速度減小量接近，水平向可達60%左右；對節點最大相對位移，豎向減小量相同，水平向NFB 略大于定剛度支座，如X向相對位移減小量NFB比定剛度多5.3%.根據表4 結果可知，兩種支座均大大減小了支座水平反力，即大跨空間結構中的柱頂剪力，NFB 的減小量略小于定剛度支座，但差值不超過1%，均為90%以上；對比兩種支座的最大位移和殘余位移可知，變剛度支座明顯小于定剛度支座，如NFB 水平Y向最大位移比定剛度支座小37%，殘余位移小84%.

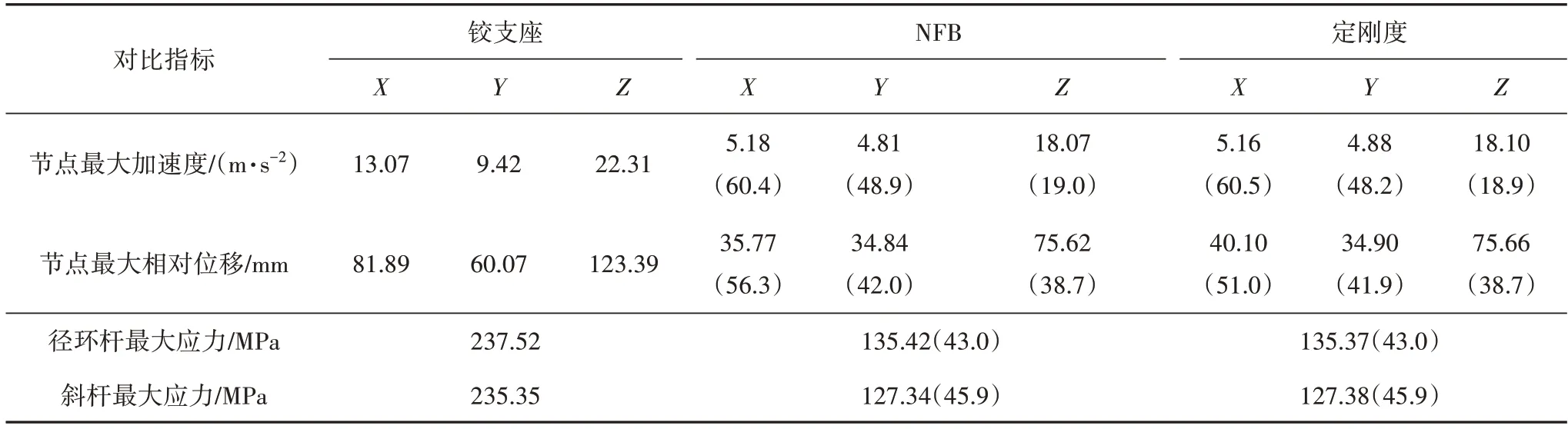
表3 節點和桿件地震響應峰值對比Tab.3 Comparison of peak seismic response of nodes and members

表4 支座地震響應峰值對比Tab.4 Comparison of peak seismic response of isolators

為更詳細、全面地對球面網殼的地震響應進行評估，對3 種結構（除最外環外）全部桿件、節點和支座的各項地震響應峰值進行對比.

圖10 為桿件應力對比圖，可以看出鉸支座結構的桿件應力分布主要范圍為（100，250），而布置了隔震支座的結構桿件應力分布范圍為（0，150），整體小于鉸支座結構，兩種隔震支座結構響應整體分布接近.圖11 和圖12 分別為相對位移和加速度對比圖，可以看到鉸支座結構各指標分布較分散，范圍較大且上限高；兩種隔震結構各指標分布較集中，范圍較小且上限減小，其中NFB 結構的節點水平相對位移整體比定剛度的小.可見安裝了隔震支座的結構地震響應減弱且整體性較好，且對節點相對位移的減弱效果NFB更優于定剛度支座.

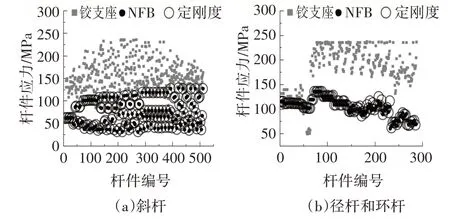
圖10 桿件應力峰值對比Fig.10 Comparison of peak stress of members

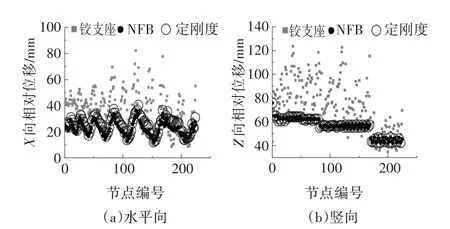
圖11 節點相對位移峰值對比Fig.11 Comparison of peak relative displacement of nodes

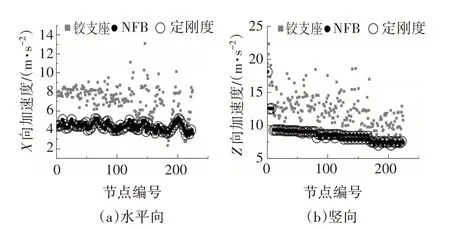
圖12 節點加速度峰值對比Fig.12 Comparison of peak acceleration of nodes

圖13 為支座水平反力峰值對比，隔震支座相對鉸支座整體明顯減小且分布較均勻.圖14 為NFB 和定剛度支座水平峰值位移對比圖，定剛度支座位移峰值分布為X（104，145）和Y（203，240），NFB 位移峰值分布為X（57，92）和Y（108，144）.圖15 為NFB 和定剛度支座殘余位移對比圖，定剛度支座殘余位移分布為X（90，127）和Y（130，165），NFB 殘余位移分布為X（12，44）和Y（0，27）.

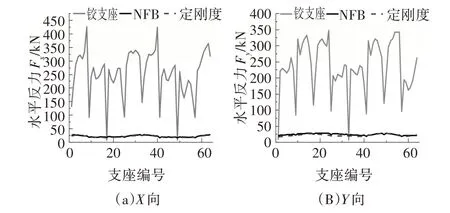
圖13 支座水平反力峰值對比Fig.13 Comparison of peak horizontal counterforce of bearings

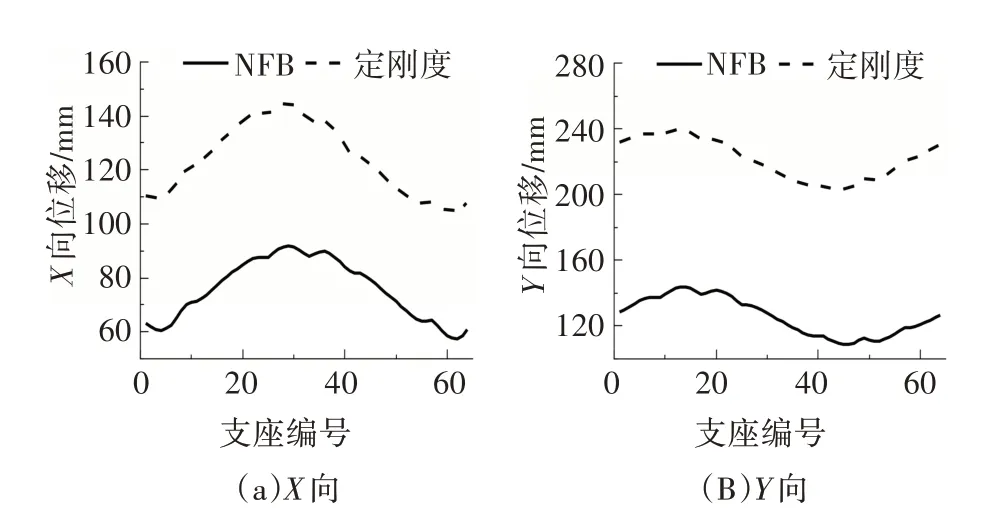
圖14 支座位移峰值對比Fig.14 Comparison of peak displacement of bearings

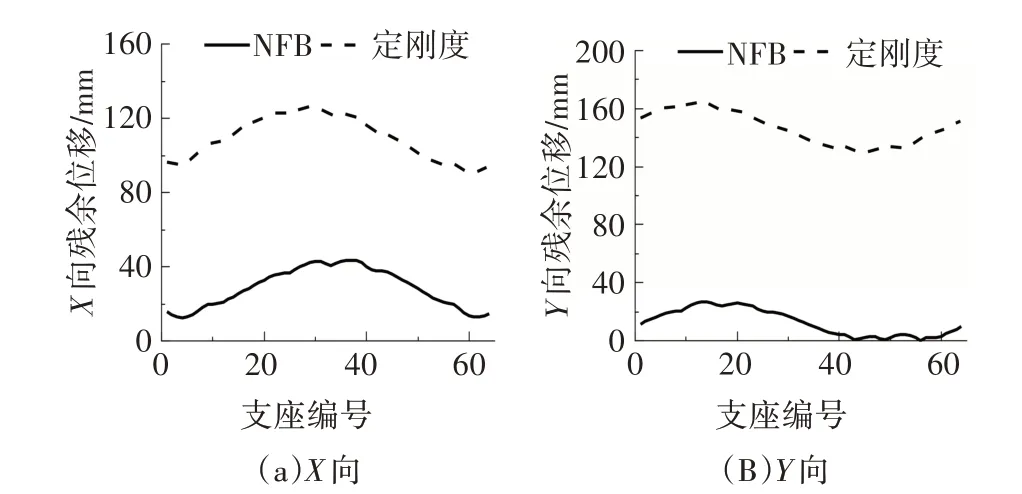
圖15 支座殘余位移對比Fig.15 Comparison of residual displacement of bearings

為方便比較兩種支座的整體隔震效果，定義一個評價指標：隔震系數ρ=隔震結構地震響應峰值的平均值∕鉸支座結構地震響應峰值的平均值，ρ值越小，減震效果越好.各項信息的對比見表5，對比可知NFB對結構節點水平相對位移的隔震系數比定剛度支座約小0.1，NFB 的平均位移峰值比定剛度小43%，平均殘余位移比定剛度小91%.

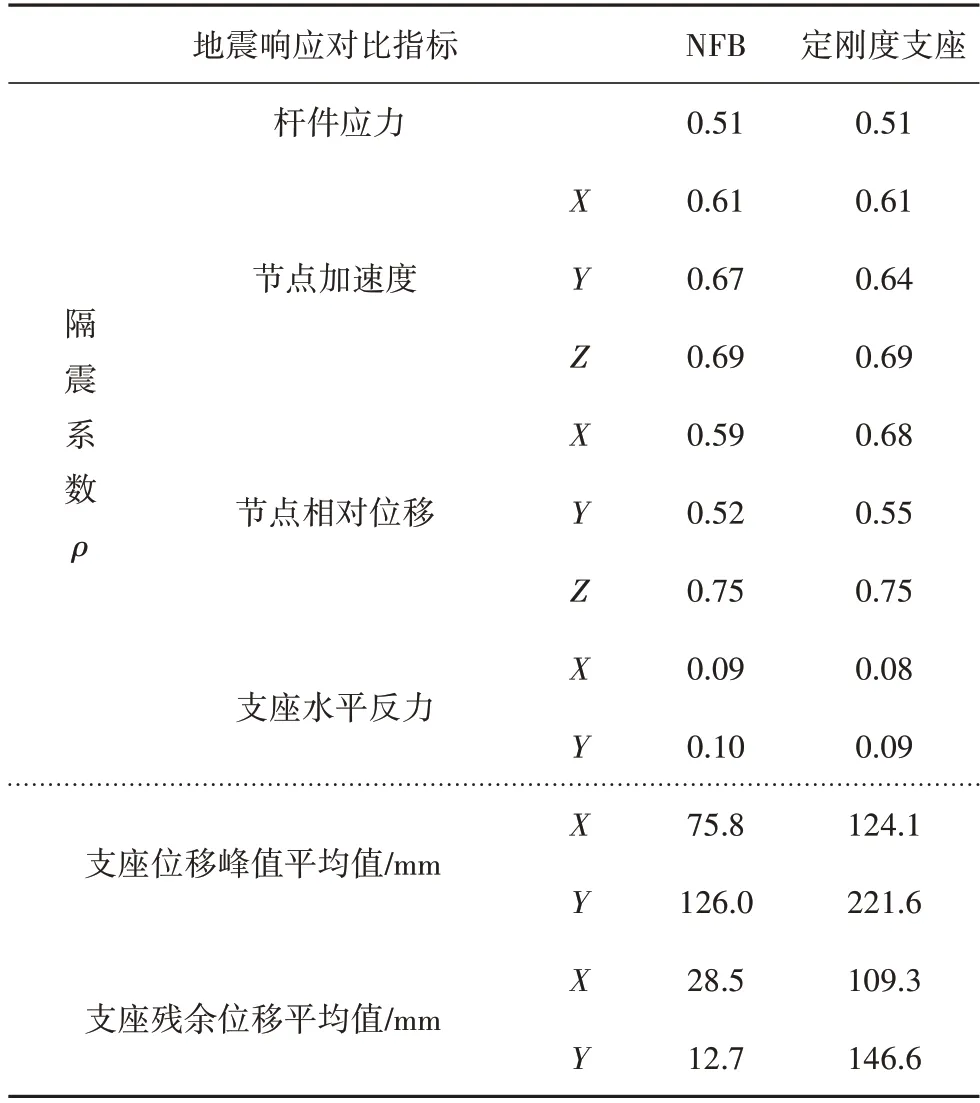
表5 整體減震效果對比Tab.5 Comparison of overall shock absorption effect

4.4 參數分析

天然地震動具有很強的隨機性，輸入的地震波不同，結構響應也會有較大差異，本文選取El-Centro波、Taft 波和一條人工波進行動力分析，加載制度同上節.安裝NFB 的網殼結構在不同地震動下的隔震系數如表6 所示，可見對于不同地震作用NFB 均對網殼結構有良好的減震效果.

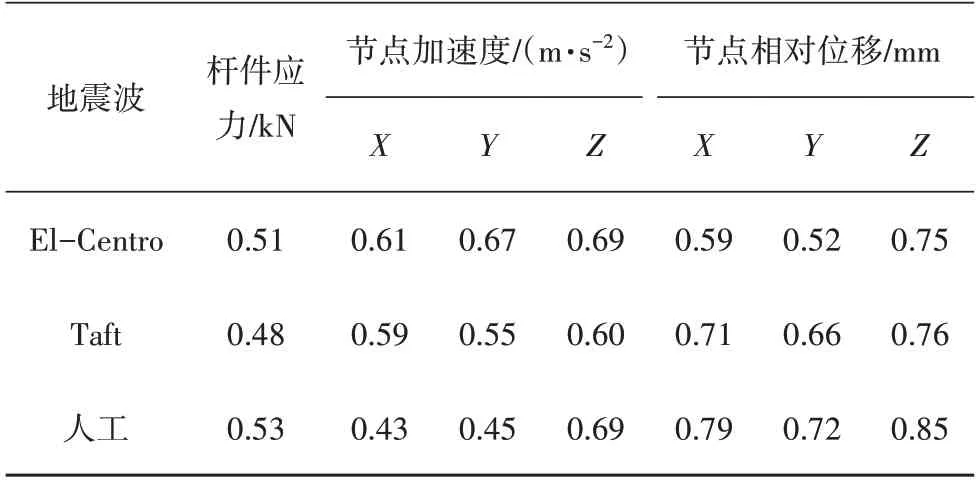
表6 不同地震波作用下整體減震效果Tab.6 Overall shock absorption effect under different seismic waves

為探討不同形體參數的網殼選用NFB 作為隔震支座的普適性，對應用NFB 的不同矢跨比球面網殼的減震效果進行分析，如表7 所示，對于不同矢跨比網殼結構，NFB 均有良好減震效果，其中矢跨比為1∕4的結構整體減震系數最小，減震效果更好.

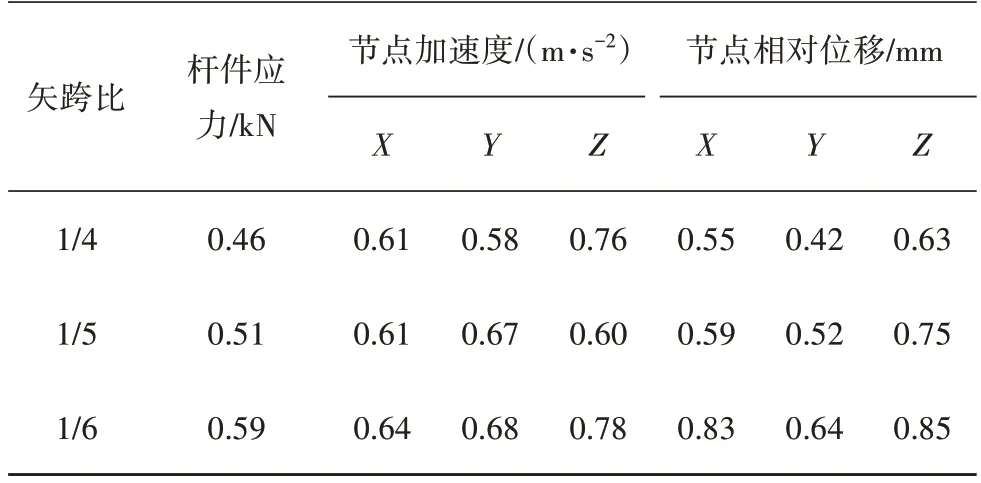
表7 不同矢跨比網殼整體減震效果Tab.7 Overall shock absorption effect of reticulated shells with different rise-span ratio

選取表2 所示支座參數，通過改變關鍵參數彈簧線徑和有效圈數研究NFB對球面網殼結構的隔震規律.結果如圖16和圖17所示，線徑小于5 mm 時隔震系數變化較小，大于5 mm 時桿件應力和水平相對位移隔震系數呈明顯上升趨勢，支座峰值位移和殘余位移都隨線徑增大而明顯減小，因而線徑取5 mm時支座的隔震性能較好；各項隔震系數受彈簧圈數影響較小，支座峰值位移和殘余位移隨有效圈數增大而增大，有效圈數越小支座自復位能力越好.

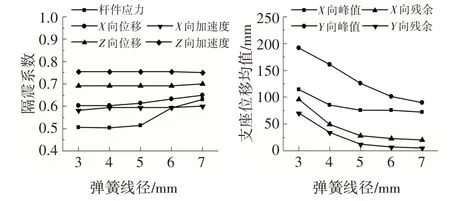
圖16 圓錐彈簧線徑影響規律Fig.16 Influence law of cone spring wire diameter

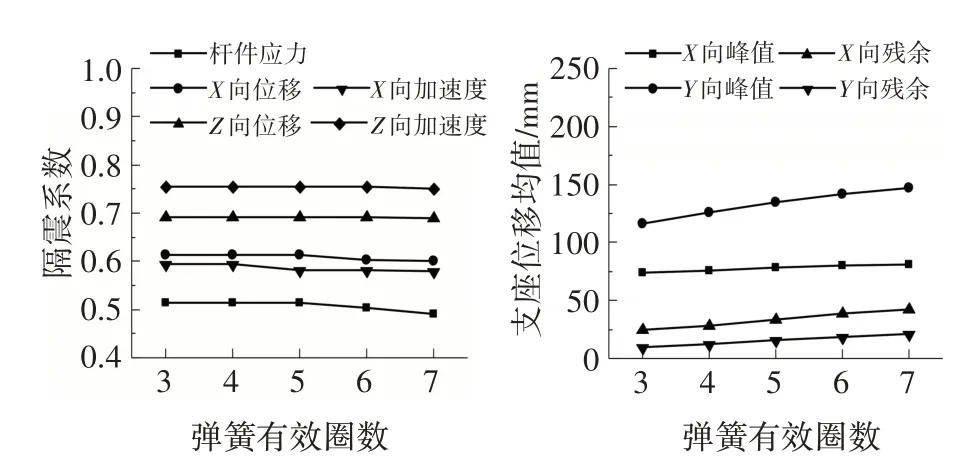
圖17 圓錐彈簧有效圈數影響規律Fig.17 Influence law of effective coil number of cone spring

5 結論

基于平面滑移支座，結合圓錐彈簧的非線性特點，提出了一種新型變剛度摩擦滑移支座（NFB），建立其實體模型進行了數值仿真分析與參數分析，將NFB 與相同初始剛度的定剛度滑動支座應用于單層球面網殼結構進行隔震分析并對比，最后研究NFB關鍵參數對隔震效果的影響規律，得出以下結論：

1）NFB 通過摩擦滑移實現隔離地震和耗能，通過均勻布置的圓錐彈簧實現各向自復位，合理設置圓錐彈簧參數使（R2-R1）≥N·d，則彈簧可壓縮至一個線徑厚度，有效節省了支座空間.

2）NFB 滯回曲線飽滿，有良好的耗能性能.NFB滑動位移較小時剛度不變，滯回響應與普通定剛度支座無異，位移超過線性臨界位移時為變剛度，且剛度隨位移的增加而增大，相對于普通定剛度滑動支座，能更有效地限制位移和提供更好的自回復能力.

3）圓錐彈簧的參數會影響NFB 的滯回響應，支座的初始剛度和非線性剛度隨線徑的增加而增大，隨有效圈數的增加而減小；支座的線性臨界位移不受線徑影響，隨有效圈數的增加而減小.

4）從單層球面網殼的非線性時程分析結果看，NFB 對網殼的水平和豎向都有良好的隔震效果，和普通定剛度支座對比顯示，對網殼的桿件應力、節點豎向加速度和豎向相對位移，兩支座隔震系數相等，隔震效果相同；對網殼的節點水平加速度和支座剪力，兩支座隔震系數相差不超過0.03，隔震效果接近；對網殼的節點水平相對位移，NFB 的隔震系數比定剛度支座小0.1 左右，NFB 的控制效果更好；對支座的位移峰值和殘余位移，NFB 的平均位移峰值比定剛度小43%，平均殘余位移比定剛度小91%，NFB對位移的控制和支座自復位能力明顯優于定剛度支座.

5）NFB 的彈簧有效圈數越小，支座自復位能力越好，彈簧線徑越大隔震系數越大，但線徑越大，支座自回復能力越強，因此，建議在保證良好回復力的前提下，選取彈簧線徑較小的支座作為隔震設備.