超音速氣流中熱塑性復合材料壁板的非線性熱顫振特性*

高藝航，段靜波，雷勇軍

(1. 國防科技大學 空天科學學院， 湖南 長沙 410073； 2. 中國運載火箭技術研究院 北京宇航系統(tǒng)工程研究所， 北京 100076；3. 石家莊鐵道大學 工程力學系， 河北 石家莊 050043)

隨著航天器朝著高速、強突防、低成本、短周期方向發(fā)展，對結構構件的材料與成型提出了更高的要求。熱塑性樹脂基復合材料由于其耐高溫、高強度、高韌性、可重復使用等諸多優(yōu)異性能，成為可重復使用航天器首選的先進復合材料。然而，熱塑性復合材料基體韌性大，受熱塑性顯著，在航天器極端復雜的氣動熱環(huán)境中，熱塑性復合材料制成的壁板類結構的氣動彈性力學行力及機理十分值得研究。

關于壁板熱顫振問題的研究最早可以追溯到 20 世紀50年代，Houbolt[1]最先開始研究溫度場均勻分布的二維壁板顫振邊界及其屈曲失穩(wěn)特性。隨后，Dowell[2]針對金屬壁板幾何非線性顫振問題進行了大量研究。Kouchakzadeh等[3]采用經典板理論和von Karman非線性位移應變關系進行結構建模，研究復合材料層合板在超音速氣流中的非線性氣動彈性問題。如果飛行馬赫數(shù)較高，在強烈的氣動加熱效應作用下，壁板將面臨極端嚴酷的熱環(huán)境。Zhou等[4]發(fā)現(xiàn)受熱壁板在氣流中的運動形式極其復雜，具有從低速氣流中的衰減振動、熱屈曲振動形式到高速氣流中各種類型的振動。楊智春等[5]采用分步分析方法研究了復合材料鋪層方式對壁板熱顫振特性的影響。李凱倫等[6]對高超聲速環(huán)境中功能梯度薄板的熱氣動彈性問題進行了研究，發(fā)現(xiàn)氣動加熱效應能夠使薄板發(fā)生熱屈曲或者提前進入振動狀態(tài)。Yang等[7-8]針對高超聲速飛行器一體化防熱結構，建立了泡沫填充復合材料波紋夾芯板的高階分層氣動彈性模型，討論了幾何參數(shù)和材料性能對顫振臨界動壓的影響。Li等[9]研究了三角形柵格芯夾層板在超音速氣流中的顫振和屈曲，并采用位移反饋的方法設計了主動控制器，為夾層結構在飛行器設計中的應用提供了理論依據(jù)。

關于熱塑性復合材料，?zen等[10]分別采用實驗和仿真分析方法研究了熱塑性蜂窩夾芯板低能量沖擊響應特性。Chen等[11]設計和制備了多層熱塑性復合材料(ThermoPlastic Composite, TPC)波紋夾芯板，采用平板壓縮試驗研究了芯材結構的失效機理。目前，公開的文獻資料大多是關于熱塑性復合材料的制造工藝、本構關系、彈塑性變形、損傷測試方面的研究[12]，而關于熱塑性復合材料壁板的顫振問題報道還比較少[13-15]。基于此，本文以熱塑性復合材料層合板為研究對象，研究其顫振特性，分析關鍵參數(shù)對壁板熱顫振特性的影響規(guī)律。

1 超音速流場中復合壁板顫振有限元方程

1.1 結構模型

如圖1所示，矩型熱塑性復合材料壁板的長度和寬度分別為L和H，厚度為h。由于復合材料壁板屬于厚板，因而，本文采用Mindlin厚板理論，壁板內任意一點的位移場可寫為：

(1)

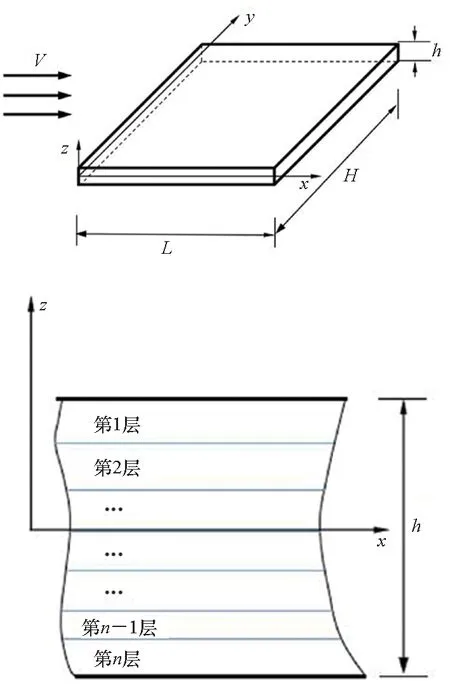
圖1 熱塑性復合材料壁板示意圖Fig.1 Sketch of thermoplastic composite panel

其中，u0、υ0、w0分別為中面上的點沿x軸、y軸和z軸方向的位移，θx和θy分別為中面法向轉角。

考慮高速氣流作用下壁板可能產生的幾何非線性變形，采用Von-Karman大變形理論，給出熱塑性壁板的應變-位移關系如下：

(2)

其中：ε0包括壁板中面面內位移產生的應變分量和壁板大變形時撓度引起的非線性應變分量；κ為彎曲時壁板的曲率向量；γ為橫向剪切應變向量；z為壁板厚度方向的坐標。

在熱塑性壁板應力-應變關系方面，考慮溫度對熱塑性壁板熱應力的影響以及材料力學性能隨溫度的變化，暫不引入應力應變的塑性本構關系，但在分析中討論屈服極限對壁板顫振應力的影響。對于第k鋪層，并忽略法向正應力，則壁板應力-應變關系為：

(3)

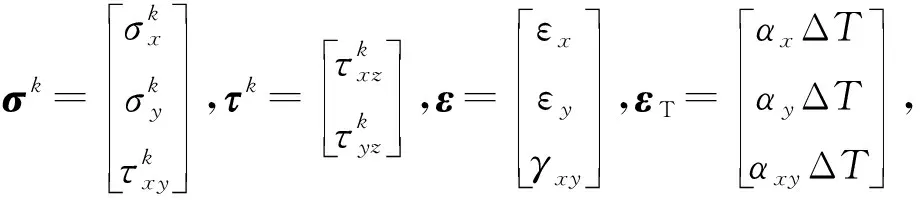
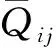
根據(jù)復合材料層合理論，n層復合變剛度壁板本構關系可寫為：

(4)

其中，N、M、Fs分別為復合變剛度壁板的膜力、彎矩、橫向剪力等內力，矩陣A、B、D、As見文獻[16]，矩陣NT、MT的表達式為：

(5)

1.2 氣動力模型

在Ma>1.6的高速氣流中，壁板顫振可采用一階準定常活塞理論計算氣動力。 當壁板表面來流沿x方向時，氣動力表達式[17]為：

(6)

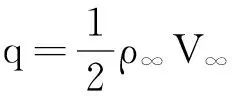
1.3 非線性顫振有限元方程

根據(jù)Hamilton原理，建立復合壁板的運動微分方程，即

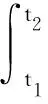
(7)

其中，δT和δU分別為虛動能和虛應變能，δW為氣動力和結構阻尼所做的虛功。

基于復合壁板本構關系、幾何關系以及氣動力模型，分別寫出壁板體積域V內的虛應變能和虛動能，以及其表面S上的外力虛功。 其中，虛應變能包括壁板振動產生的應變能δUM和熱載荷產生的應變能δUΔT兩部分，具體如下：

(8)

運用有限元方法求解壁板顫振，采用四邊形四節(jié)點板單元對壁板進行網格離散，總體位移列陣可記為如下形式：

(9)

其中

(10)

將總體位移列陣代入式(8)，通過變分則可獲得壁板的有限元顫振方程：

(11)

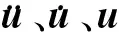
(12)

1.4 復合材料屈服準則

基于Hill正交各向異性屈服準則，Chen和Sun提出了適用于各向異性纖維增強復合材料的三維塑性勢函數(shù)。Weeks和Sun進一步假設復合材料在纖維方向1上是線彈性的，在纖維方向2～3 面內是橫觀各向同性的，從而將三維塑性勢函數(shù)簡化為[14]：

(13)

本文研究的熱塑性C/PPS材料為緞紋機織復合材料，材料在纖維方向1、2上是線彈性的，且不考慮纖維方向3(厚度方向)的正應力σ33，因而，上述塑性勢函數(shù)可最終退化為：

(14)

2 算例驗證與分析

2.1 正確性驗證

根據(jù)文獻[18]中T300/5208型環(huán)氧樹脂復合材料壁板算例，壁板幾何尺寸為0.3 m×0.12 m，厚度為1 mm，具體材料參數(shù)取值及顫振動壓無量綱化與文獻[18]一致，采用本文程序進行了固有頻率及顫振速度計算，結果見表1和表2。從表1中可以看出，本文計算的固有頻率與文獻結果吻合較好。采用有限元法分析時，通常需要通過細密網格才能保證分析結果的精度。因此，需要進行網格收斂性驗證。

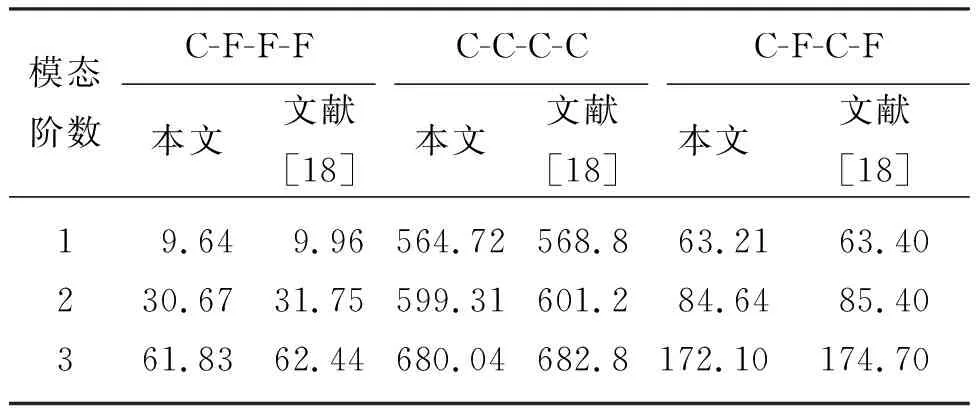
表1 環(huán)氧樹脂復合材料壁板固有頻率

從表2中可以看到，隨著網格劃分數(shù)量增多，結果逐漸收斂。當網格劃分數(shù)為40×16時，本文顫振速度計算結果與文獻吻合得很好。因此，綜合考慮線性壁板顫振的計算精度和效率，本文后續(xù)計算均采用40×16的網格數(shù)量。

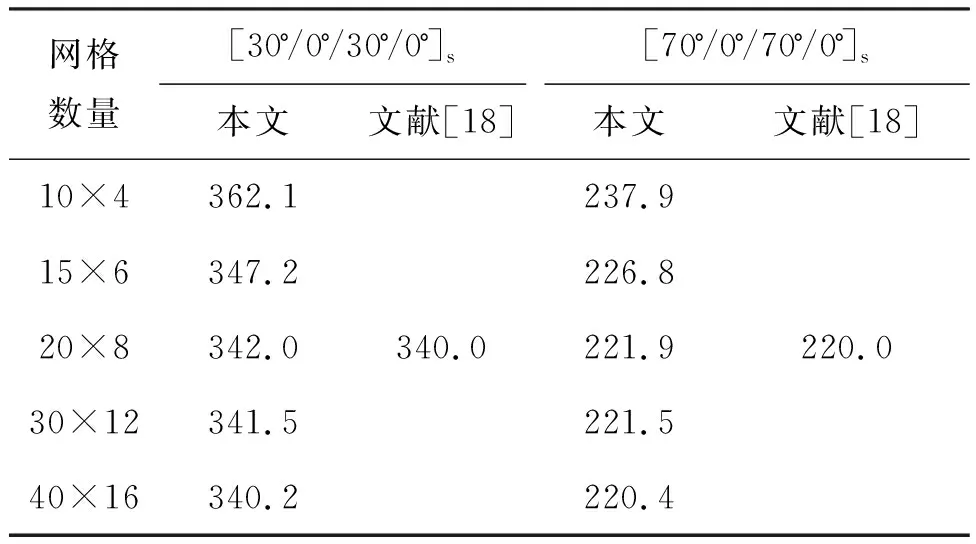
表2 環(huán)氧樹脂復合材料壁板無量綱顫振動壓

2.2 頻域線性顫振分析

以四邊簡支的C/PPS熱塑性復合材料矩形壁板為對象，采用有限元法求解研究其熱固有特性和頻域熱顫振特性。熱塑性復合材料密度為0.9～1.6 g/cm3，本文計算中取1.25 g/cm3，泊松比取0.08，熱膨脹系數(shù)取1.6×10-6℃，其隨溫度變化的材料力學性能參數(shù)見表3[15]。壁板幾何尺寸為0.4 m×0.2 m，厚度為3 mm，鋪層方式為[0]7，來流方向平行于x軸。

表3 熱塑性材料力學性能參數(shù)

由于溫度載荷不僅產生熱應力，而且溫度還改變材料的力學性能，這兩方面均對壁板顫振產生影響。熱塑性材料受溫度變化影響較大，需要同時考慮兩方面的影響。本文采用V-g法求解熱塑性復合材料壁板頻域顫振特性，并分析材料力學性能隨溫度變化對熱塑性復合材料壁板熱顫振特性的影響。

圖2分別給出了60 ℃和90 ℃下壁板前兩階模態(tài)阻尼隨無量綱動壓的變化規(guī)律。壁板無量綱顫振動壓定義見文獻[19]。從圖2中可以看到，兩種溫度下壁板熱顫振均由1階模態(tài)和2階模態(tài)耦合引起。在60 ℃下，由阻尼曲線在來流動壓為211.0時過零點，這說明壁板的無量綱顫振動壓為211.0。同樣，在90 ℃下，由阻尼曲線過零點可得知，壁板無量綱顫振動壓為149.5。

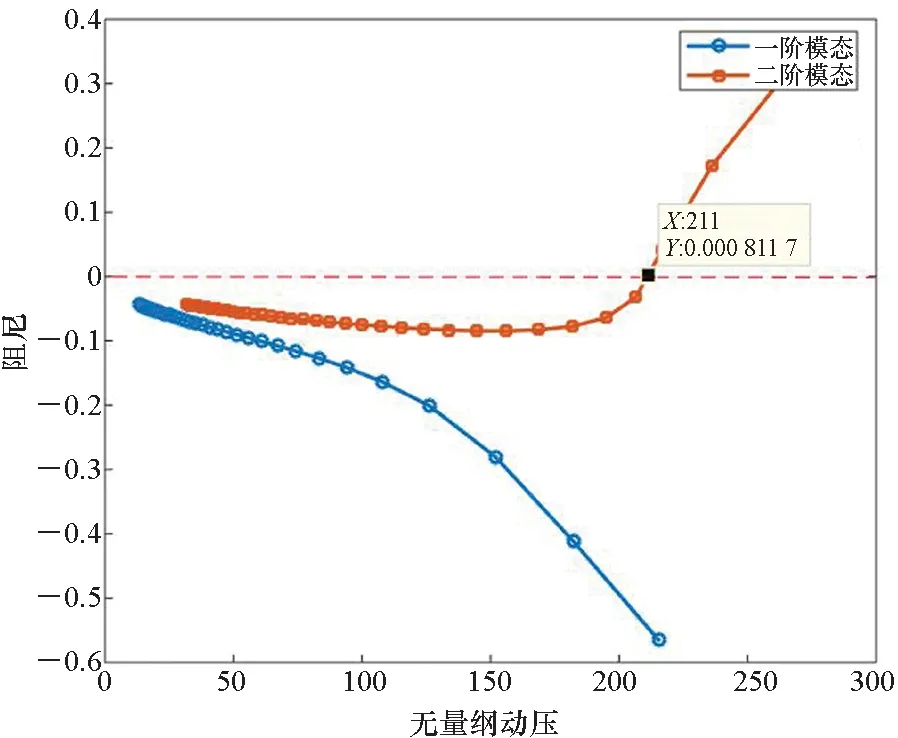
(a) 60 ℃下壁板的模態(tài)耦合(a) Modal coupling of the panel at 60 ℃

圖3給出了23 ℃、60 ℃、90 ℃、120 ℃四個溫度下考慮與不考慮材料性能隨溫度變化兩種情況下熱塑性壁板的熱顫振特性。總體上看，溫度的升高顯著降低了壁板的顫振動壓。在常溫23 ℃下，壁板顫振無量綱動壓最大。考慮熱塑性材料溫變后得到的壁板無量綱動壓低于僅考慮熱應力時的顫振動壓，從圖3中可以看到，在60 ℃、90 ℃、120 ℃下，壁板無量綱動壓分別降低了5.1、17.0、34.8。由此可得出，考慮材料性能隨溫度變化后，得出的壁板顫振動壓更低，而且溫度越高，材料性能隨溫度變化對壁板顫振特性影響越明顯。

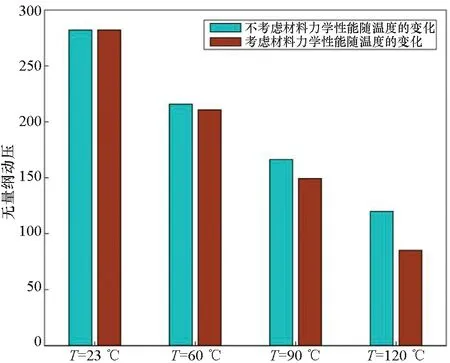
圖3 不同溫度下熱塑性壁板熱顫振動壓Fig.3 Thermal flutter dynamic pressure of thermoplastic panels at different temperatures

2.3 時域非線性顫振分析

以四邊簡支的C/PPS熱塑性復合材料壁板為對象，采用有限元法從時域求解壁板非線性熱顫振特性。

圖4～6給出了60 ℃時熱塑性復合材料壁板特征點(0.5a，0.5b)在不同來流速度下的顫振時間歷程和相平面圖。從圖4可以看到，當來流動壓λ=188.6時，壁板受到初始擾動后，振動是收斂的，這表明動壓未達到顫振臨界動壓。當來流動壓λ=213.7時，壁板受到初始擾動后，進入極限環(huán)振動，振幅數(shù)量級為1.7×10-3mm，此時動壓超過顫振臨界動壓，壁板做周期振動，發(fā)生顫振，如圖5所示。當動壓進一步增大，取來流動壓λ=234.7時，壁板受到初始擾動后，仍處于顫振極限環(huán)振動，但是壁板做周期振動的振幅增大為4.3×10-1mm，如圖6所示。

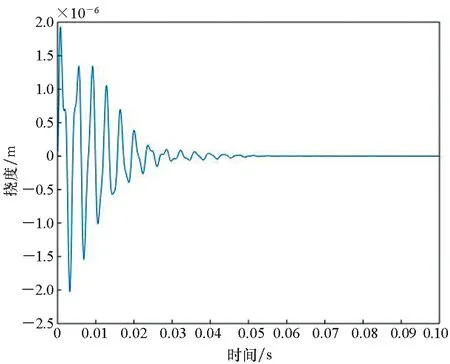
(a) 板中點位置撓度-時間曲線(a) Time history plot of deflection at the centre of the plate

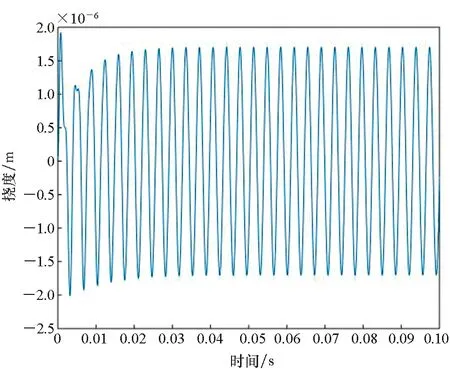
(a) 板中點位置撓度時間曲線(a) Time history plot of deflection at the centre of the plate

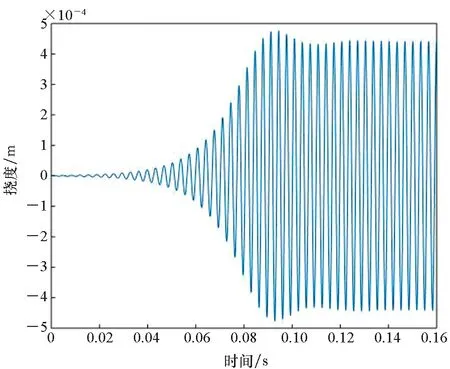
(a) 板中點位置撓度時間曲線(a) Time history plot of deflection at the centre of the plate

圖7給出了熱塑性復合材料壁板在23 ℃、60 ℃、90 ℃、120 ℃下壁板極限環(huán)振幅隨無量綱動壓的變化情況。從圖7中可以看出，不同溫度下壁板的顫振極限環(huán)振幅隨動壓的增大而增大，增大趨勢基本一致。但隨著溫度從23 ℃逐漸增加到120 ℃，壁板進入顫振的動壓越來越低。此外，從圖7中還可以看出考慮與不考慮材料性能隨溫度變化對壁板極限環(huán)振幅的影響。在常溫23 ℃下，兩者沒有差異。在60 ℃下，考慮材料力學性能隨溫度變化時，壁板進入顫振的動壓低于不考慮材料力學性能隨溫度變化的情況。與此同時，相同動壓下，考慮材料力學性能隨溫度變化時的極限環(huán)振幅要高于不考慮材料力學性能隨溫度變化的情況。在90 ℃、120 ℃下，規(guī)律相似于60 ℃的情形，只是壁板進入顫振的動壓差值隨著溫度從60 ℃到120 ℃逐漸增大，相同動壓下，極限環(huán)振幅差異也越來越大。

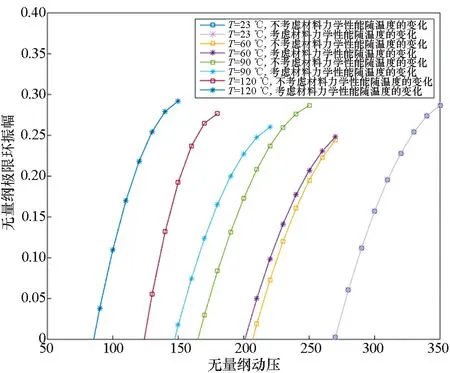
圖7 不同溫度下壁板極限環(huán)振幅隨無量綱動壓的變化Fig.7 Change of limit cycle amplitude of the panel along with dimensionless dynamic pressure at different temperatures

2.4 顫振應力分析

文獻[15]給出的不同溫度下剪切試驗數(shù)據(jù)表明，C/PPS熱塑性材料剪切強度都隨著溫度的增加而出現(xiàn)明顯的降低，在120 ℃時剪切強度比常溫時降低了63.64%。對于熱塑性壁板，在顫振發(fā)生過程中，如果應力響應達到材料塑性屈服強度將引起不可恢復的永久變形，這是熱塑性壁板熱顫振設計中需要考慮的問題。下面仍以四邊簡支的C/PPS熱塑性復合壁板為例，研究壁板顫振亞臨界過程中的應力變化情況。

圖8給出了熱塑性復合材料壁板分別在23 ℃、60 ℃、90 ℃、120 ℃下，壁板極限環(huán)振蕩下等效應力幅值隨動壓變化的情況。從圖8中可以看到，在同一溫度下，隨著動壓增大，壁板的應力水平在增大。例如在23 ℃時，隨著壁板顫振動壓由280.5增加到322.1，顫振等效應力由0.399 MPa增加到1.27 MPa；在60 ℃時，隨著壁板顫振動壓由220.2增加到216.7，顫振等效應力由0.462 MPa增加到0.840 MPa。比較不同溫度下壁板的顫振等效應力，可以看出，隨著壁板溫度的升高，在溫度應力和材料溫變的共同作用下，壁板顫振等效應力是逐漸降低。原因在于，溫度產生的結構溫度應力是壓應力，而壁板顫振產生的應力是反向的拉應力，兩者呈現(xiàn)相互抵消的效應，且溫度越高，抵消效應越明顯。此外，從圖8中可以發(fā)現(xiàn)，壁板極限環(huán)振蕩下等效應力幅值總體較小，均沒有達到各溫度下C/PPS熱塑性復合材料的屈服極限(見表3)，壁板沒有出現(xiàn)屈服區(qū)域。這主要是由于壁板顫振過程中產生的主要是雙向拉或壓應力狀態(tài)，切應力較小，而等效應力則是反映切應力水平，因而壁板極限環(huán)振蕩下等效應力幅值總體較小。

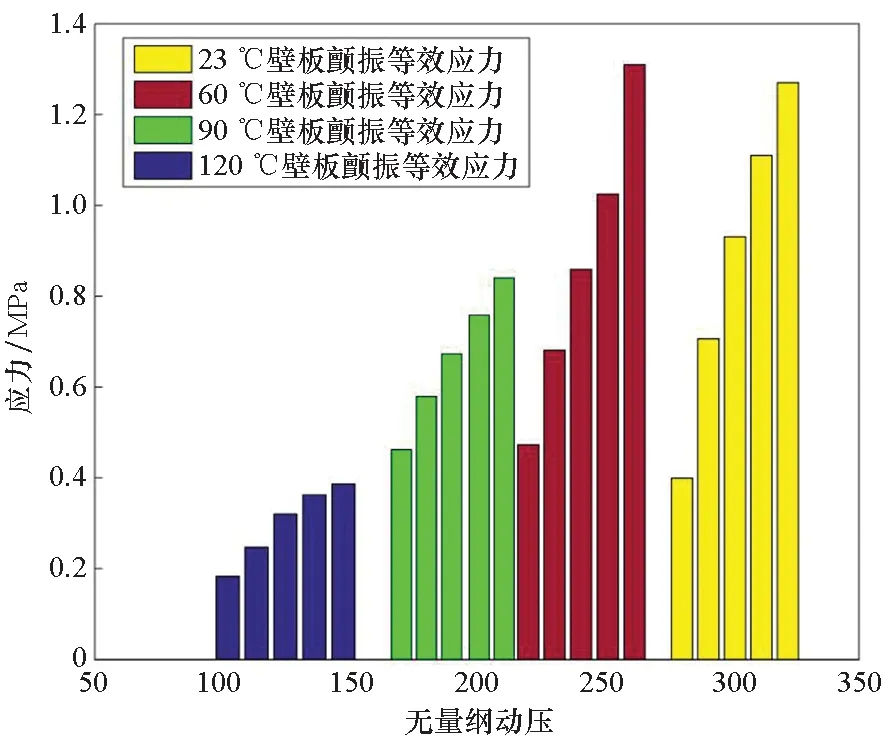
圖8 不同溫度下壁板極限環(huán)振蕩等效應力變化Fig.8 Change of limit cycle oscillation equivalent stress of the panel at different temperatures

3 結論

本文建立了超音速流場中熱塑性復合材料壁板熱顫振的有限元模型，與相應文獻結果進行對比，驗證了本文模型及算法的正確性。進而采用V-g法、Newmark法分別從頻域、時域求解復合變剛度壁板顫振特性，得出的主要結論如下：

1)熱塑性壁板熱顫振由1階模態(tài)(縱向一彎)和2階模態(tài)(縱向二彎)耦合產生，隨著溫度的升高，壁板的顫振動壓顯著降低，而且考慮熱塑性材料溫變特性后得到的壁板顫振動壓要低于僅考慮熱應力時的顫振動壓。

2)不同溫度下，當考慮材料力學性能隨溫度變化時，壁板進入顫振的動壓低于不考慮材料力學性能隨溫度變化的情況。與此同時，相同來流動壓下，考慮材料力學性能隨溫度變化時的極限環(huán)振幅要高于不考慮材料力學性能隨溫度變化的情況。

3)隨著壁板溫度的升高，壁板顫振等效應力是逐漸降低的，而且壁板極限環(huán)振蕩下等效應力水平總體較低，均沒有達到各溫度下復合材料的屈服極限。