彎矩作用下熱塑性復合材料懸臂梁彈塑性分析*

雷勇軍，劉明偉，張大鵬，高藝航

(1. 國防科技大學 空天科學學院， 湖南 長沙 410073； 2. 空天任務智能規劃與仿真湖南省重點實驗室， 湖南 長沙 410073；3. 中國運載火箭技術研究院 北京宇航系統工程研究所， 北京 100076)

自1951年Bradit首次制造熱塑性復合材料(玻璃纖維增強聚苯乙烯)以來，熱塑性復合材料已普遍應用于航空工程、汽車交通、醫療器械等領域[1-3]。在當前可重復使用運載器的需求下，具備高抗沖擊性能、高損傷容限以及可熔融再加工等特點[4-5]的熱塑性復合材料必將在航天工程領域得到更廣泛運用。試驗表明[6-7]熱塑性復合材料具有明顯的彈塑性階段，進入塑性后有較強的承載能力，這與傳統的熱固性復合材料彈性階段后即發生脆性斷裂有很大不同。為充分發揮材料的應用潛力，避免以彈性設計代替塑性設計的錯誤[8]，對熱塑性復合材料彈塑性力學特性進行分析具有重要意義。

熱塑性復合材料具有高度正交各向異性特點，其力學問題可等效為正交各向異性材料的力學問題進行研究。Lekhnitskii[9]得到了受橫向力作用的正交各向異性懸臂梁、受均布載荷和線性分布載荷作用的正交各向異性簡支梁和懸臂梁的彈性解答。黃德進等[10-11]利用Airy應力函數建立了均布載荷下正交各向異性梁的力學特性分析模型，并得到了兩端固支和一端固支一端簡支邊界條件下應力場和位移場的解析解。針對均布載荷作用下正交各向異性懸臂梁的變形問題，黃立新等[12-13]用有限元法分析了材料各向異性、跨高比等對變形的影響。Klc等[14]分析了在均布載荷或橫向集中力作用下復合材料懸臂梁自由端撓度與纖維方向角之間的關系。然而上述文獻中應力函數形式很難確定，為解決這一問題，張浪等[15]給出了一種通過求解函數方程獲得平面各向異性梁彈性解的新方法。當外載荷較大，材料進入塑性后，相應問題變得更復雜。基于理想彈塑性理論，Aykul和Kaya[16]以及Esendemir[17-18]研究了集中載荷下熱塑性復合材料懸臂梁、均布載荷下或集中載荷下簡支梁的彈塑性應力問題，然而理想彈塑性理論與實際熱塑性復合材料應力應變關系存在較大差異。結合線性強化彈塑性理論和Euler-Bernoulli梁假設，Sayman等[19]對彎矩作用下熱塑性復合材料懸臂梁進行研究，得到了彈性解和彈塑性解。對于復合材料短粗梁，Karamanl[20]利用Timoshenko梁理論研究了復合材料層合梁在不同邊界條件下的變形問題；Balduzzi等[21]基于Timoshenko梁理論分析了材料的各向異性對梁的本構關系和應力分布的影響；Doeva等[22]給出了考慮拉彎剪扭耦合效應的Timoshenko復合材料梁靜撓度分析的精確解析解，并指出現有的Euler-Bernoulli梁模型不足以解釋厚梁特性的問題。但是，以上基于Timoshenko梁理論的研究均沒有考慮熱塑性復合材料的塑性效應。

本文以熱塑性復合材料懸臂梁為研究對象，基于Timoshenko梁理論和Tsai-Hill屈服準則，得到應力和位移的解析解。通過與文獻[19，21]和有限元計算結果對比，驗證本文所給模型與方法的正確性，并分析了纖維方向角、彎矩、跨高比以及纖維體積分數等對懸臂梁應力和位移的影響規律。

1 懸臂梁彈塑性分析模型

研究對象如圖1所示，熱塑性復合材料懸臂梁長為l、高為2c、厚為t，纖維方向角為θ，自由端承受彎矩M作用，忽略體力，并建立如圖所示的坐標系xoy。

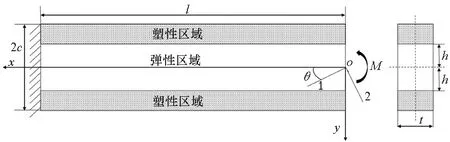
圖1 受彎矩載荷的懸臂梁Fig.1 Cantilever beam loading by bending moment

不失一般性，對該懸臂梁進行如下4個基本假設：

1)梁的變形屬于小撓度變形；

2)在xoy平面內滿足平面應力假設；

3)熱塑性復合材料是拉壓同性的；

4)懸臂梁變形滿足Timoshenko梁理論，軸向位移u、橫向位移v和轉角φ相互獨立，則有

(1)

其中，u0為梁中性面軸向位移，w為梁中性面橫向位移。

下面分別建立彈性段和彈塑性段理論分析模型。

1.1 彈性段分析模型

考慮懸臂梁的平面應力問題，基本方程如下：

1)平衡方程

(2)

2)幾何方程

(3)

3)本構方程

(4)

在纖維坐標系1o2下，熱塑性復合材料的本構關系為

(5)

(6)

其中，轉換矩陣T的表達式為

(7)

設應力函數為φ(x,y)，其與應力σx、σy和τxy的關系為

(8)

結合式(3)、式(4)和式(8)得控制方程

(9)

梁僅在自由端承受彎矩M，因此在梁任意截面上可以得到

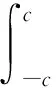
(10)

由彎矩M為給定常值可知，σx只與坐標y有關，結合式(8)可得應力函數的表達式為

φ=F(y)+yA(x)+B(x)

(11)

其中，F(y)、A(x)、B(x)為待求函數，對于本懸臂梁，其上下表面為主要邊界條件，則有

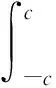
推導可得在彎矩M作用下懸臂梁彈性階段應力場和位移場為

(12)

由式(12)可知，當彎矩M較小時，梁處于彈性階段，梁上下表面處應力最大；隨著M增大，梁上下表面先進入塑性狀態，需結合復合材料塑性力學知識建立彈塑性段分析模型。

1.2 彈塑性段分析模型

文獻[23-25]表明Tsai-Hill屈服準則描述的應力空間屈服面與熱塑性復合材料真實屈服狀態吻合，本文基于Tsai-Hill屈服準則對熱塑性復合材料懸臂梁彈塑性段應力和變形進行分析，平面應力假設下考慮拉壓同性的Tsai-Hill屈服準則如下：

(13)

其中，X為復合材料沿纖維方向屈服強度，Y為垂直纖維方向屈服強度，S為面內剪切強度。根據式(13)，定義等效應力為

(14)

根據坐標轉換矩陣，材料主軸坐標系下應力σ1、σ2、τ12和xoy坐標系下應力σx、σy、τxy的轉換關系為：

(15)

由于σy=0、τxy=0，將式(15)代入式(14)中，可得等效應力表達式為

(16)

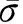
(17)

其中，σ0的大小為X，K是塑性常數，則復合材料屈服時滿足如下關系：

(18)

其中，X1為復合材料達到屈服條件時應力σx的大小，即當σx=X1時，材料進入塑性。選用相關塑性流動法則，在纖維坐標系1o2下塑性應變增量表達式為

(19)

總應變增量為彈性應變增量和塑性應變增量之和，即dε=dεe+dεp，則纖維坐標系1o2下總應變增量為

(20)

對式(20)進行積分，可得到纖維坐標系1o2下各應變分量，再利用坐標轉換關系，將其變換到xoy坐標系下，可得xoy坐標系下總應變為

(21)

其中，B1、B2和B3為與材料塑性性能和纖維方向角有關的參數。梁在出現屈服后，結合Timoshenko梁理論可得

(22)

由1.1節分析可知，σx與坐標y成正比例關系，梁的塑性區域從梁上下表面向中性面擴展，設y∈(-h,h)為彈性區域，則在彈塑性分界位置存在σx=X1，可得

(23)

由式(23)并結合轉角邊界條件φ(l,y)=0得

(24)

(25)

因此考慮塑性后，懸臂梁的應力解如下：

(26)

在梁的任意截面均滿足如下關系：

(27)

基于Timoshenko梁理論并結合式(24)，可得軸向位移為

(28)

由式(3)和式(21)積分可得橫向位移在彈性區域和塑性區域分別為

(29)

(30)

其中，Ve(x)和Vp(x)為與x相關的待求函數。進一步由邊界條件ve(l,0)=0、vp(l,h)=0和連續性條件ve(x,h)=vp(x,h)可得橫向位移的表達式為

(31)

(32)

以上分析將Timoshenko梁理論和塑性線性強化理論應用于熱塑性復合材料懸臂梁的彈塑性分析中，并獲得了梁應力和變形的解析解。此外，由于熱塑性復合材料的力學性能與纖維體積分數vf有關[26-27]，本文所建模型可用于分析不同纖維體積分數下熱塑性復合材料懸臂梁彈塑性力學特性。

2 算例分析

2.1 模型驗證

文獻[19]基于Euler-Bernoulli梁理論和線性強化彈塑性本構模型分析了彎曲載荷下熱塑性復合材料懸臂梁彈塑性應力和變形；文獻[21]基于Timoshenko梁理論分析了在彎曲載荷下雙層復合材料懸臂梁的彈性靜變形。為驗證本文所建模型及求解方法的正確性，以文獻[19]中的編織鋼纖維增強聚乙烯復合材料懸臂梁為例進行對比分析，算例中涉及的基本參數與文獻[19]一致：懸臂梁長80 mm、高12 mm、厚6.4 mm，彈塑性力學參數如表1所示。設θ為45°，M為4 kN·mm。此外，本節給出了梁有限元計算結果，有限元計算采用四節點雙線性平面應力四邊形單元，共計2 600個單元，屈服準則為各向異性Tsai-Hill屈服準則[28]，硬化方式為各向同性硬化。

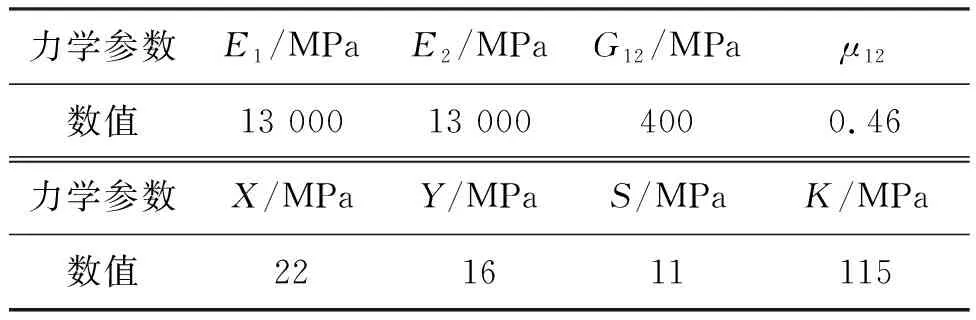
表1 編織鋼纖維增強聚乙烯復合材料力學參數

圖2給出了本文模型與參考文獻[19，21]以及有限元計算在懸臂梁固定端截面應力分布對比結果。由圖2(a)可知，在不考慮塑性的情況下，以上方法獲得的數據吻合較好；由圖2(b)可知，在考慮塑性的情況下，本文所建模型與有限元計算結果更接近。對比圖2(a)和圖2(b)可知，塑性效應會顯著改變懸臂梁截面應力分布形式。表2給出了以上方法在自由端下表面點(0 mm,6 mm)的應力和位移。由表2可以看出，本文模型所得數據較文獻[19]均更接近于有限元計算結果，特別是在考慮塑性的情況下，軸向位移和橫向位移較文獻[19]的Euler-Bernoulli梁模型提高了1.81%和2.03%的計算精度。以上分析驗證了本文所建模型和求解方法的正確性，說明了在熱塑性復合材料懸臂梁彈塑性力學分析中，運用Timoshenko梁理論可顯著提高求解精度。下面基于本文模型對纖維方向角、彎矩、跨高比以及纖維體積分數等對梁應力和變形的影響做進一步分析。

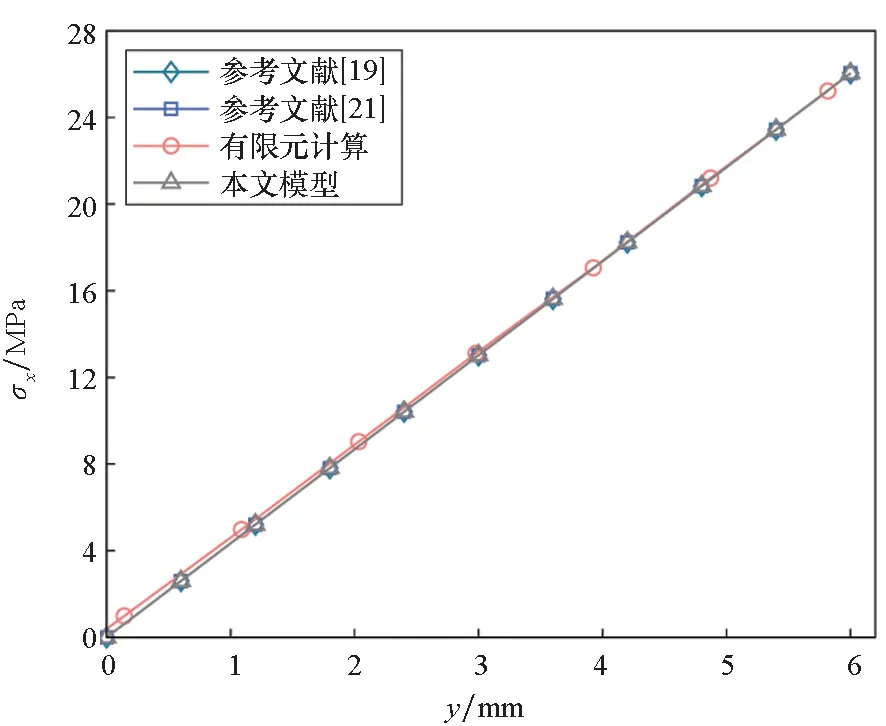
(a) 不考慮塑性(a) Not considering plasticity

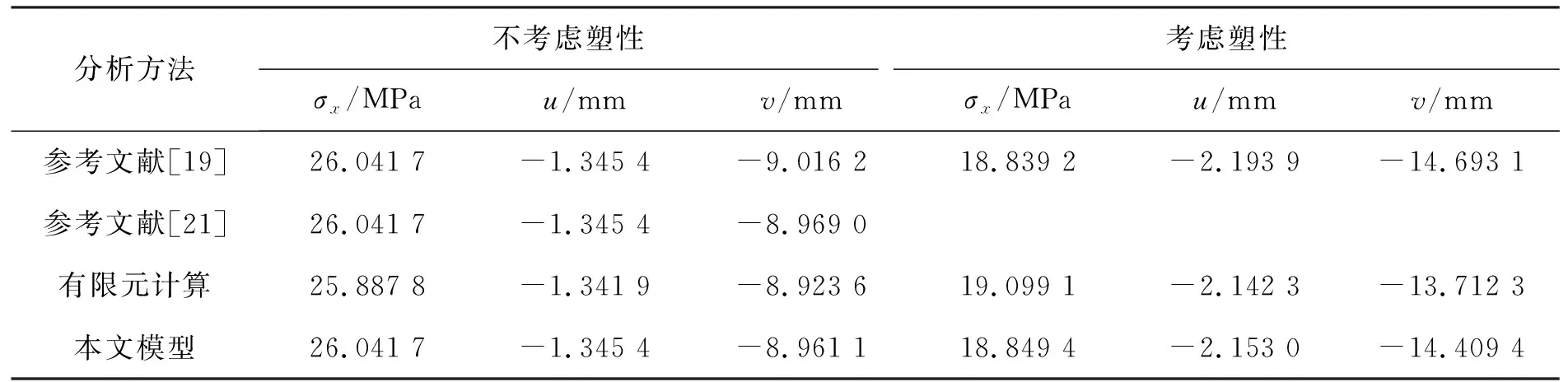
表 2 參考點(0 mm，6 mm)應力、位移

2.2 影響因素分析

2.2.1 纖維方向角對懸臂梁彈塑應力和位移的影響

圖3分別給出了纖維方向角θ對彈塑性區域參數h、梁自由端下表面點應力σx、軸向位移u以及橫向位移v的影響情況。在本算例中，梁的幾何參數和彈塑性力學參數同2.1節。

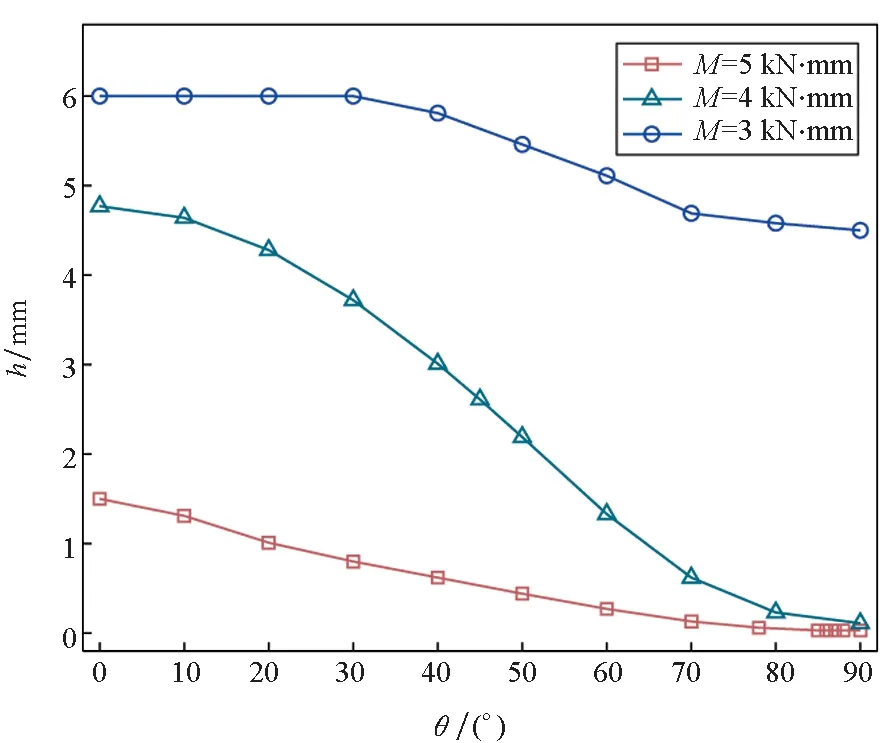
(a) 參數h隨纖維方向角θ的變化曲線(a) Relation of parameter h and fiber orientation angle θ

由圖3(a)可知，在不同M作用下，h均隨著θ增大而減小，h越小表明梁處于塑性的區域范圍越大，這說明增大θ會顯著降低梁的剛度，且該影響隨著M的增大而增強。

由圖3(b)可知，當M為3 kN·mm且θ不超過30°時，σx幾乎不受θ的影響。在此條件下參考點處于彈性狀態，由式(12)可知該狀態下應力大小與纖維方向角無關。當參考點處于塑性狀態時，參考點應力與纖維方向角的關系分兩種情況：當M較小時，σx隨θ增大而減小；當M較大時，σx隨θ的增大而先增大后減小。塑性應力σx的解析表達式(26)可對上述變化做出解釋。由式(26)可知，塑性應力σx與塑性各向異性參數N成反比而與等效塑性應變εp成正比，又由N的表達式可知N隨θ的增大而增大，式(25)表明εp與h成反比，h隨θ的增大而減小。

由圖3(c)和圖3(d)可知，當M為3 kN·mm且θ小于30°時，參考點的位移隨θ增大而增大，注意在此情況下，參考點處于彈性狀態。當參考點進入塑性狀態后，不同彎矩作用下的位移隨纖維方向角的變化表現出不同的規律，位移解析式可對此做出合理解釋。以軸向位移u為例，由式(28)可知，軸向位移u與彈塑性區域參數h成反比、與X1成正比，結合式(18)，X1與參數N成反比，由此可知軸向位移u與h和N的乘積成反比。下面結合圖3(c)中M為5 kN·mm的情況做進一步解釋，由圖可知u隨θ增大而先增大后減小，這是由于參數N與參數h的乘積隨θ增大而先減小后增大。橫向位移v的分析也如此，在此不做過多贅述。

2.2.2 彎矩對懸臂梁彈塑應力和位移的影響

為進一步分析彎矩M和纖維方向角θ對梁應力和位移的影響，在本算例中，θ分別為0°、30°和60°，梁的其他幾何參數和材料參數同2.1節。圖4分別給出了在給定纖維方向角下，梁彈塑性區域參數h、梁自由端下表面點應力σx、軸向位移u和橫向位移v與彎矩M之間的關系。

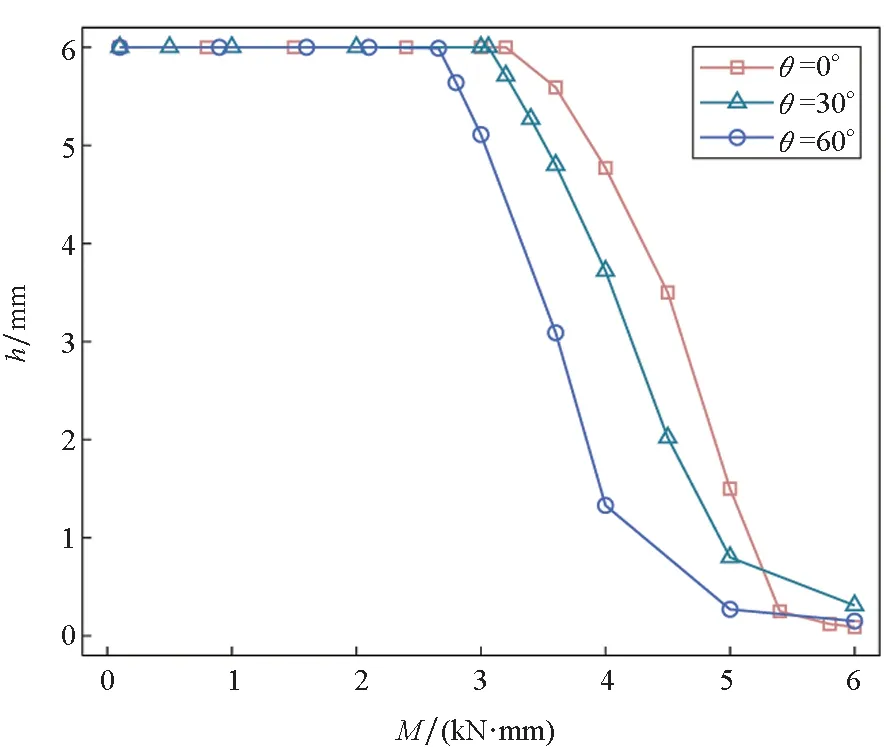
(a) 參數h隨彎矩M的變化曲線(a) Relation of parameter h and moment M

由圖4(a)可知，h隨著M的增大先保持不變后快速減小。當M較小時，梁并未出現屈服，h大小始終為梁高的一半，隨著M增大，梁上各點逐漸屈服，導致h顯著減小。

由圖4(b)可知，在梁截面出現屈服前，σx隨著M增大而線性增大，在屈服后，σx隨著M先緩慢增大后快速增大。由式(26)可知，σx與h成反比，當梁剛屈服時，h值較大因而σx增加緩慢，隨著M繼續增大，梁截面塑性區域面積增加，h顯著減小，從而導致σx迅速增大。

由圖4(c)和圖4(d)可知，當M較小時，參考點處于彈性狀態，此時位移隨M增大而緩慢增大，當參考點屈服以后，其位移隨著M增大而迅速增大。此外，從圖中可以看出當θ為60°且M超過4 kN·mm時，參考點的位移尤其是橫向位移v已經很大，此時已不滿足小變形假設。

2.2.3 跨高比對懸臂梁彈塑應力和位移的影響

在分析跨高比l/(2c)對梁應力和位移的影響時，用h/c表征彈性區域占整個截面面積的比例，h/c的值越接近1，說明梁截面彈性區域面積越大。圖5分別給出了在不同載荷下h/c以及梁自由端下表面參考點的應力σx、軸向位移u、橫向位移v與跨高比l/(2c)的關系。在本算例中，通過改變梁高度2c來改變梁跨高比，纖維方向角θ固定為30°，梁其他幾何參數和材料參數同2.1節。

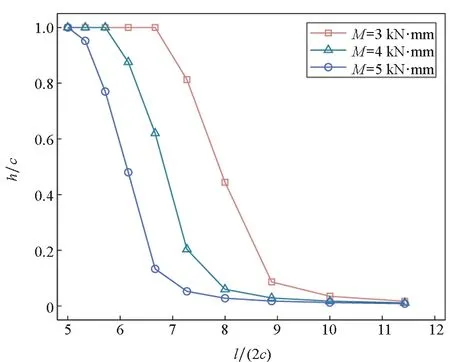
(a) 參數h/c隨跨高比l/(2c)的變化曲線(a) Relation of parameter h/c and aspect ratio l/(2c)

由圖5(a)可知，隨著跨高比l/(2c)增大，h/c的值從1逐漸減小至0，且跨高比l/(2c)大于9時，梁截面已完全進入塑性狀態。這說明在梁長度一定的情況下，梁的高度越小，梁更易屈服。由圖5(b)可知，跨高比l/(2c)越大，σx值越大，而且M越大，σx隨跨高比l/(2c)增加得越快。參考點的變形情況與跨高比l/(2c)的關系如圖5(c)和圖5(d)所示，無論是軸向位移還是橫向位移，當跨高比l/(2c)較小時，其隨跨高比l/(2c)的增加而增加緩慢，當跨高比l/(2c)較大時，其隨跨高比l/(2c)的增加而增加迅速。由以上分析可知大跨高比梁結構偏柔，更易屈服。由圖可以看到，當跨高比l/(2c)大于8時，參考點的變形量已超出小變形假定的范圍。

2.2.4 纖維體積分數對懸臂梁彈塑性區域分布和應力的影響

本小節分析纖維體積分數vf對懸臂梁應力和彈塑性區域分布的影響。在本算例中懸臂梁材料為芳綸纖維增強聚丙烯復合材料，其力學參數同文獻[26]一致，詳細如表3所示，梁其他幾何參數和材料參數同2.1節，設置兩種工況：①外載荷M=3 kN·mm、纖維方向角θ=30°；②外載荷M=2 kN·mm、纖維方向角θ=45°。圖6給出了當vf在10%至25%之間時，梁自由端下表面點應力σx和彈塑性區域參數h隨其的變化曲線。

表3 芳綸纖維增強聚丙烯復合材料力學參數

由圖6(a)可知，vf越大，σx越小。由表3可知，隨著vf增加，復合材料彈性力學性能均提高，相同彎矩作用下，σx越小。由圖6(b)可知，隨著vf增加，兩種工況下參數h均逐漸減小。當vf=10%時，h接近于6 mm，整個梁截面處于彈性狀態；當vf=25%時，h接近于0，整個梁截面處于塑性狀態。由表3可知，在塑性力學參數方面，隨著vf增加，纖維方向屈服強度增大，但垂直纖維方向以及面內剪切屈服強度顯著降低。根據Tsai-Hill屈服準則，復合材料整體更易屈服，因此在相同彎矩作用下，纖維體積分數越大，梁截面塑性區域面積越大。

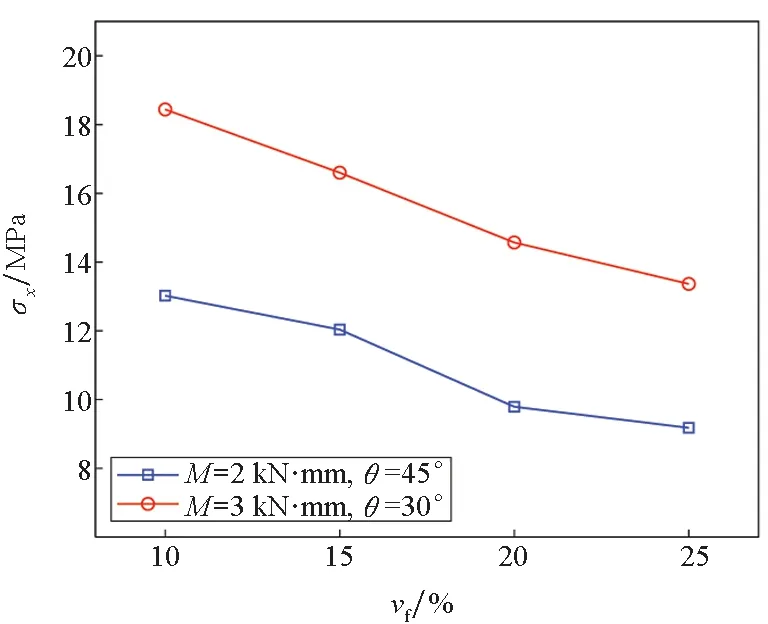
(a) 應力σx隨纖維體積分數vf的變化曲線(a) Relation of stress σxand fiber volume fraction vf

3 結論

本文基于Timoshenko梁理論和Tsai-Hill屈服準則建立了彎矩作用下熱塑性復合材料懸臂梁彈塑性分析模型，得到了應力和位移的解析解，并對梁截面彈塑性應力和變形的影響因素進行了分析，主要結論包括：

1)在熱塑性復合材料懸臂梁彈塑性特性分析中，基于Timoshenko梁理論得到的應力和位移精度更高。對于編織鋼纖維增強熱塑性復合材料，本文模型所得軸向位移和橫向位移分別比Euler-Bernoulli梁理論提高了1.81%和2.03%。

2)纖維方向角θ和彎矩M綜合影響熱塑性復合材料懸臂梁力學特性，當M較大時，截面最大應力和位移隨著θ增大而增大；當M較小時，截面最大應力隨著θ增大而減小，位移隨著θ增大而先增大后減小。

3)跨高比l/(2c)顯著影響熱塑性復合材料懸臂梁彈塑性力學特性，在相同彎矩作用下，跨高比l/(2c)越大，截面最大應力和位移越大，梁截面塑性區域面積相對越大，且當跨高比l/(2c)超過9時，熱塑性復合材料懸臂梁已完全進入塑性狀態。

4)當單向纖維增強聚丙烯復合材料纖維體積分數由10%增加至25%時，懸臂梁由彈性狀態進入完全塑性狀態，且隨著纖維體積分數增加，懸臂梁截面最大應力逐漸減小。

以上結論可為熱塑性復合材料懸臂梁設計應用提供參考，在后續研究中，將進一步考慮熱塑性復合材料拉壓異性的力學特性建立相關結構的力學模型。