基于軸對稱內聚力單元的立貯發動機黏接界面結構完整性分析*

王君祺，鮑福廷，崔輝如

(1. 西北工業大學 航天學院, 陜西 西安 710072; 2. 陸軍工程大學 國防工程學院, 江蘇 南京 210007)

固體火箭發動機依靠結構簡單、使用操作便捷和可靠性高的特點，被廣泛用作火箭彈、導彈和探空火箭的發動機，以及航天器發射和飛機起飛的助推裝置[1]。

反應速度快、殺傷力強、命中精度高、服役時間長、控制范圍廣以及安全性高將導彈的設計和研發提到了前所未有的高度。其中，安全性能高是一切指標的基礎，也是制約導彈性能提升的關鍵。導彈長期處于戰備狀態，受發射環境的限制，發動機需要長期處于豎直存放的狀態，發動機黏接界面的力學性能將面臨嚴峻的考驗[2-6]。黏接界面的脫黏效應將直接導致發動機燃面的變化，使得發動機的內彈道特性偏離初始的設計。

不少研究人員針對發動機黏接界面上的應力情況開展了一系列的研究。韋震等[7]利用內聚力單元并結合雙線性的內聚力本構關系，研究了推進劑和絕熱層黏接界面的Ⅰ型斷裂力學行為。類似的方法同樣應用在推進劑/襯層Ⅰ型[8]以及Ⅱ型界面[9-11]。Zhou等[12]利用內聚力單元建立了襯層的有限元模型，研究了發動機中推進劑/絕熱層界面間的應力奇異特性。馬曉琳[5]通過二維平面內聚力單元構建了絕熱層和推進劑黏接界面的有限元模型，研究了發動機受波浪載荷以及點火增壓狀態等典型工況下黏接界面的力學響應。考慮到結構的軸對稱特性，平面內聚力單元處理軸對稱問題是不合適的。

本文從軸對稱內聚力單元的參考坐標系出發，依次推導了單元的分離位移、內力矢量以及單元剛度矩陣。采用旋轉體分離測試，驗證單元的準確性。開展立貯發動機黏接界面的結構完整性分析。

1 軸對稱內聚力單元

1.1 單元位移變換矩陣推導

如圖1所示，在ROZ平面內建立一個初始厚度忽略不計的軸對稱內聚力單元，與之相連接的實體單元為四節點軸對稱單元。

圖1 軸對稱內聚力單元Fig.1 Axisymmetric cohesive element

圖2給出了變形后的軸對稱內聚力單元。在單元中線方向設立橫軸，過中線的中點垂直于中線的方向為縱軸建立變形后內聚力單元參考坐標系。

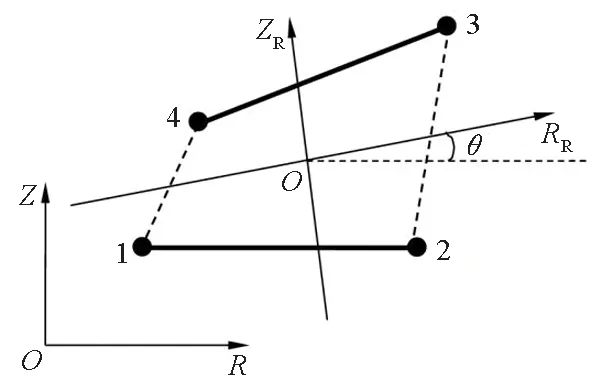
圖2 變形后的軸對稱內聚力單元Fig.2 Axisymmetric cohesive element after deformation

單元節點位移在全局和參考坐標系中的關系滿足

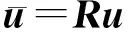
(1)

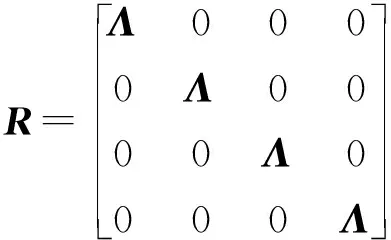
(2)

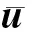
(3)

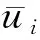
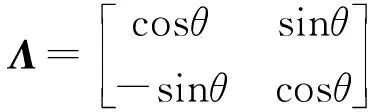
(4)

(5)

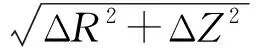
1.2 單元分離位移場推導

針對零厚度單元的情況，節點1和節點4以及節點2和節點3是分別重合的，如圖3所示。軸對稱內聚力單元在變形后的分離位移分別為

(6)

其中，Δ1和Δ2為中線左端點(節點1和節點4)的徑向分離位移以及法向分離位移，Δ3和Δ4為中線右端點(節點2和節點3)的徑向分離位移以及法向分離位移。

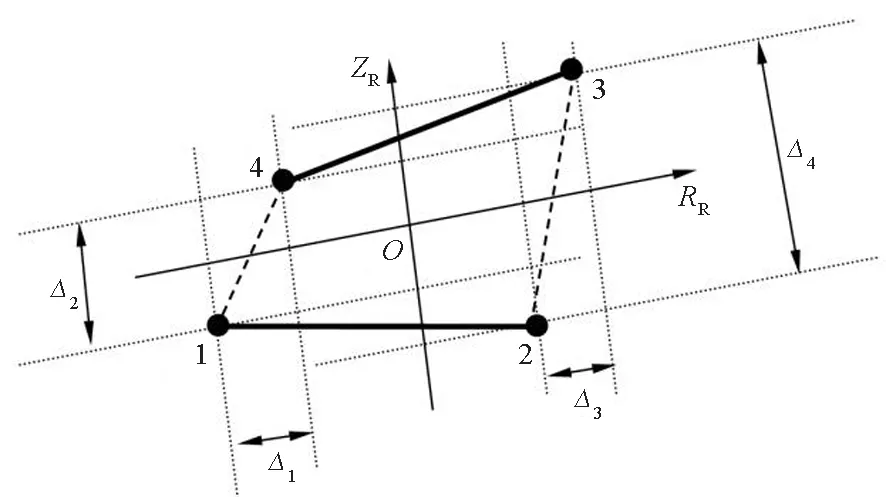
圖3 參考坐標系中的分離位移示意Fig.3 Diagram of separation displacement in the reference coordinate

利用矩陣形式可以表示為

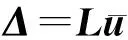
(7)

式中，

Δ=[Δ1Δ2Δ3Δ4]T

(8)

利用一維等參元理論，建立分離位移場與節點分離位移之間的關系，即

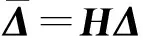
(9)

建立中線上分離位移場與節點整體位移間的關系，即

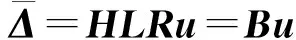
(10)

1.3 單元內力矢量及單元剛度矩陣推導

依據虛位移原理，有

(11)

式中：E和S分別代表格林應變張量和第二PK應力張量；Δ和Tc分別代表分離位移以及內聚力，Γc是指單元中線；Text以及u代表外力以及節點位移矢量，Γ為整個單元所圍成的區域。

結合伽遼金法和等參元理論，推導可得單元的剛度矩陣以及內力矢量分別為

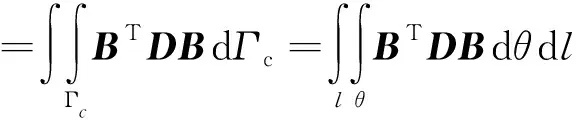
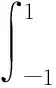
(12)

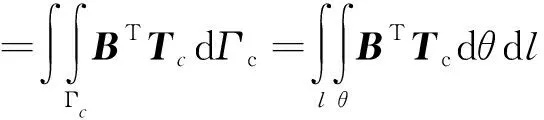
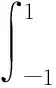
(13)

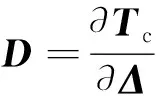
2 驗證算例

2.1 旋轉體模型

圖4給出了一個軸對稱柱狀旋轉體的子午面示意圖，旋轉體的內外徑分別為2 mm和4 mm，高為4 mm。沿著子午面的中心與水平方向呈45°的位置存在貫穿整個板的黏接界面。旋轉體的底部固支，頂部施加豎直方向的位移載荷。本驗證算例中，位移的拉伸速率為0.1 mm/s，在達到指定位移1 mm時開始松弛40 s。旋轉體的楊氏模量以及泊松比分別為10 MPa和0.33。本算例中，除了利用軸對稱單元對結構進行建模，還采用不同環向單元數量的三維網格進行對比分析，其中環向網格的數量分別為6、18以及54。

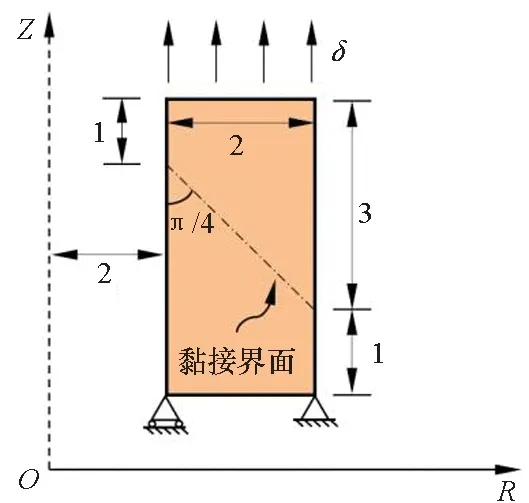
圖4 旋轉體子午面Fig.4 Meridian surface of the rotating body

2.2 黏彈性內聚力模型

PPR內聚力模型是Park等提出的考慮物理斷裂參數以及連續斷裂邊界的勢相關內聚力模型[13]，該模型的勢函數表達式為

(14)

式中：Γn和Γt為能量常數；m和n為無量綱參數；αk和βk為模型的形狀參數，分別控制法向和切向的內聚力和分離位移曲線下降段的凹凸特性；δn和δt為模型的法向和切向的臨界位移；φt和φn分別代表切向和法向內聚能，其表達式為

(15)

σmax和τmax代表法向和切向內聚強度。

Cui等[14]提出了基于參數松弛的黏彈性PPR內聚力模型，其具體形式為

(16)

黏接界面初始內聚強度σmax和τmax、初始臨界位移δn和δt、初始無量綱參數m和n分別為0.5 MPa、0.5 MPa，2.5 mm、2.5 mm，0.167 2以及0.167 2。形狀參數αk和βk均為3.10，黏彈性系數u=0.3，τ=50 s。

2.3 仿真結果分析

圖5表示不同模型在加載階段的徑向和軸向的支反力隨時間的變化趨勢。由圖5可以明顯地看到，三維模型的結果曲線隨著網格規模的不斷增加，逐漸收斂于軸對稱模型的分析結果曲線。仿真結果表明，構建的軸對稱內聚力單元是準確的。

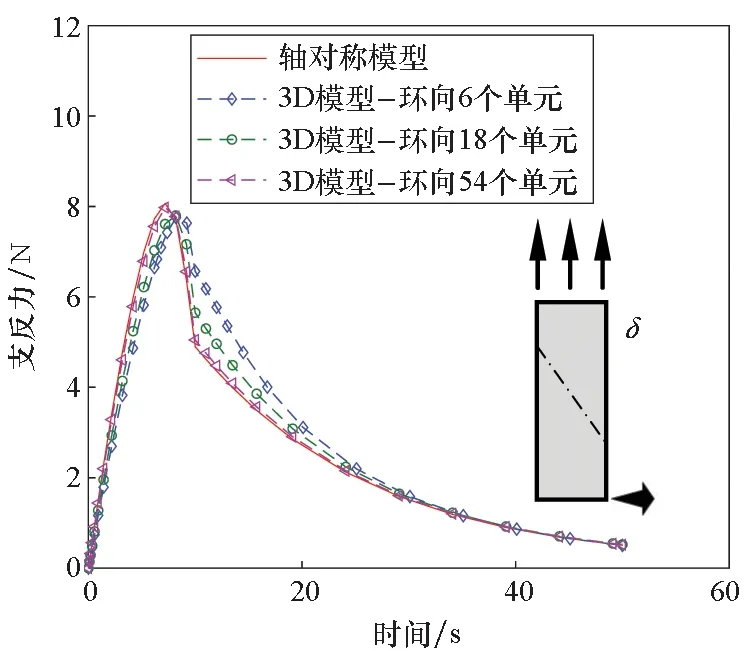
(a) 徑向(a) Radial direction

圖6給出了四種有限元模型總的自由度、單元數以及計算耗時的情況。為了比較方便，這里假設軸對稱模型的自由度、單元數以及計算耗時都為單位1。可以明顯地看到，隨著環向網格數量的增多，三維模型的自由度、單元數以及計算耗時劇烈增加。尤其是當環向的網格數量增加到54個的時候，三維模型的自由度和單元數是軸對稱模型的300多倍，而三維狀態下的耗時甚至達到了軸對稱模型的600多倍。以上分析結果表明，采用軸對稱內聚力單元計算模型是經濟高效的仿真手段。

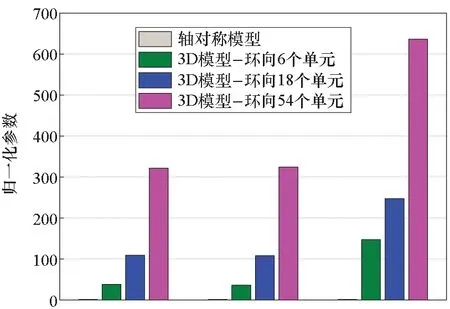
圖6 計算模型對比Fig.6 Comparison of computational models

3 立貯發動機黏接界面的力學性能研究

3.1 發動機有限元模型

對立貯式發動機在長時間貯存狀態以及受到軸向過載時的結構完整性進行分析是進行軸對稱內聚力單元開發的主要任務之一。圖7所示為某發動機簡化后的軸對稱幾何以及部分有限元網格模型。發動機整體長度為630 mm，推進劑和絕熱層部分的長度為570 mm，其中，圓管段、翼槽段以及星孔段的長度分別為300 mm、43 mm和227 mm。圓管段和星孔段推進劑的厚度分別為73 mm和48.5 mm，絕熱層和殼體的厚度分別為2 mm和3 mm。此外，由于涉及軸對稱計算，發動機中軸線和各部位的相對位置如圖7所示。為了簡化網格規模并保證計算精度，在遠離黏接界面處采用稀疏的網格規模，在黏接界面兩側對網格進行加密。推進劑、絕熱層以及殼體內聚力單元的材料屬性和文獻[15]一致。

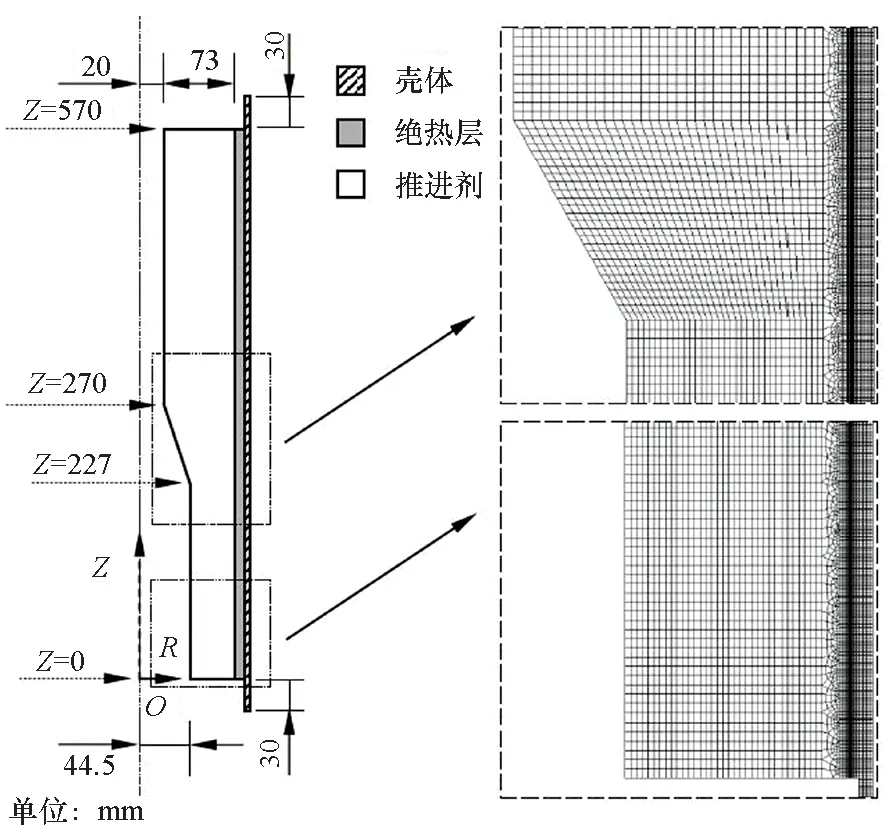
圖7 發動機軸對稱模型Fig.7 Axisymmetric model of solid rocket motor

圖8所示為發動機在點火上升階段受到的三種軸向加速度變化曲線，假設加速時間為200 s。

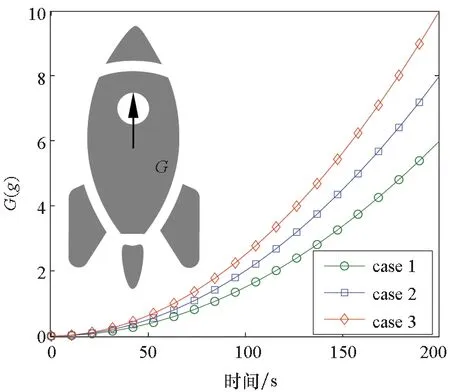
圖8 軸向加速度示意Fig.8 Diagram of axial acceleration

3.2 軸向加速度影響分析

發動機黏接界面應力分布如圖9所示，切向內聚力在黏接界面上的分布差異較大，加速度因子的增加會提升界面上切向內聚力的整體水平。切向內聚力在黏接界面的兩端會出現突變，這與黏接界面兩端受到直接的約束有關。此外，在翼槽段的兩側，翼槽段與圓管段和星孔段過渡的地方可以看到明顯的內聚力改變。對于法向內聚力而言，由于向上的加速度作用，慣性力在發動機的尾部集中，因此，在黏接界面的底部，法向內聚力達到了最高水平，并且隨著加速度因子的增加而加劇。在圓管段和星孔段，法向內聚力水平較低。尤其在星孔段，部分黏接界面處的法向內聚力已經接近于零，加速度因子在這些部位的影響較小。在翼槽段，由于黏接界面兩側變形的不協調，法向內聚力有輕微的增加，但是相比于黏接界面的底部，這部分的法向內聚力仍處于較低水平。與切向內聚力類似，加速度因子的增加會提升界面上法向內聚力的整體水平。

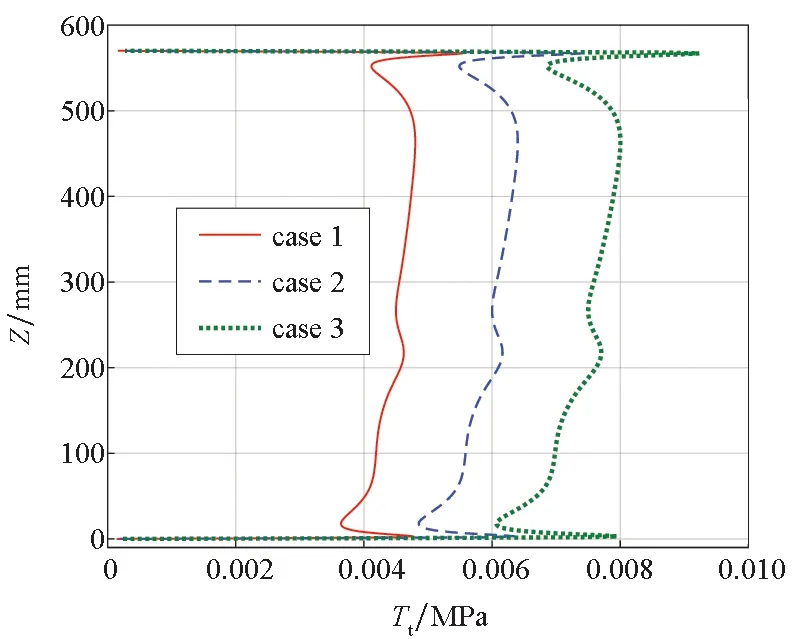
(a) 切向(a) Tangential direction

3.3 波浪載荷影響分析

艦載導彈在服役期間需要長時間受到海上波浪的影響，考慮到艦船空間有限以及為減少導彈的發射準備時間，發動機往往需要豎直存放在發射筒內。因此，海面上的波浪載荷將直接作用在黏接界面上。

一般而言，波浪載荷對艦船的影響可以分解成三個方向的振動，沿著船艏方向的縱搖、沿著左舷方向的橫搖以及垂直方向的垂搖。考慮到軸對稱模型特定的使用環境，這里僅分析對黏接界面影響較為惡劣的垂搖。研究表明，艦船的振動曲線和浪級(海況級數)之間有著一定的關聯。艦船垂搖隨海況級數之間的關系為

az(ti)=Δaz[1+kz(l-2)]sin(2π·fz·ti)

(17)

式中：az(ti)表示ti時刻的垂搖加速度；Δaz為垂搖的加速度幅值，Δaz=rand(100 mm/s2,1 000 mm/s2)；kz為加速度放大系數，kz=0.24；l為海況級數，fz為ti時刻豎直方向的波浪頻率，fz=rand(0.1 Hz, 1 Hz)。

圖10給出了不同海況級數下，發動機黏接界面上最大的切向和法相內聚力隨著時間的變化。

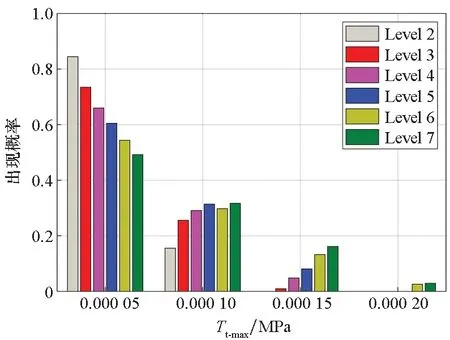
(a) 切向(a) Tangential direction

從分布上看，隨著海況級數的提高，出現高水平內聚力極值的可能性越大。和點火發射時的過載作用相比，波浪作用產生的切向內聚力表現得十分微弱。但是，這也從另一個方面說明，波浪作用下，黏接界面在切向上是比較安全的。

圖11給出了不同海況下，切向內聚力和法向內聚力極值出現部位隨時間的變化曲線。可以發現，極值出現的位置無一例外地都分布在黏接界面的兩端。這說明，在波浪載荷引起的垂向加速度的作用下，黏接界面上接近發動機頭部和尾部的位置是需要著重分析和加固的。另外不難分析，隨著海上執勤時間的延長，黏接界面上的損傷會逐漸累積，從而引起黏接界面的局部開裂等嚴重危害。

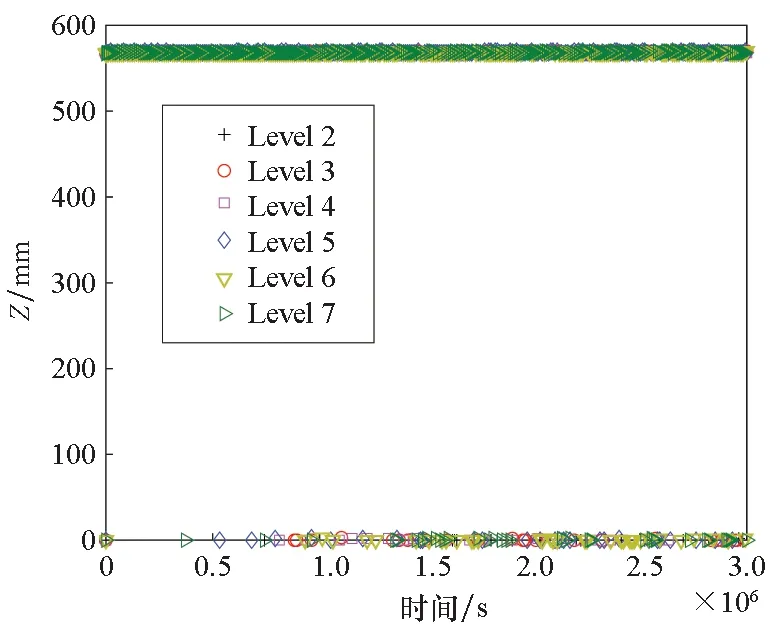
(a) 切向(a) Tangential direction

4 結論

本文研究了軸對稱內聚力單元在立貯發動機黏接界面結構完整性分析中的應用。通過構建參考坐標系的形式，建立了單元節點位移和單元內力以及單元矩陣之間的聯系。利用三維以及軸對稱網格分別開展旋轉體的分離試驗，計算結果表明，軸對稱內聚力單元可以準確和高效地進行軸對稱問題的仿真模擬。開展了立貯發動機在軸向加速度以及波浪載荷下，黏接界面的力學響應分析。仿真結果顯示，加速度因子和海況級數的提高會提升界面上內聚力的整體水平。內聚力極值分布在黏接界面的兩端，在設計階段需要重點關注。

致謝

延世大學Kyoungsoo Park(樸景秀)副教授在軸對稱內聚力單元推導方面提供了很大的幫助和指導，謹致謝意！