基于Z-score 模型的學員分組答辯成績組間差消除辦法*
楊小軍 馮 斌 柏志堯 董 方
(1.國防大學聯合勤務學院后勤與裝備信息資源教研室 北京 100858)(2.國防大學聯合勤務學院教學考評中心 北京 100858)
1 引言
答辯是一種常用的考核方法,通常將答辯成績和筆試成績兩者結合,將兩部分成績各賦以一定的權重,用計算得出的綜合成績來作為考核人員的最終成績。由于答辯需要被考核人員按順序依次進行,如果只安排一組進行答辯,會導致時間成本較高。因此,在實際組織答辯時,都是抽簽將學員分成幾組,幾組同時進行答辯。作為主導答辯的老師,都會力求客觀公正地評價每名學員的成績。各組的老師在學員答辯時,都是嚴格按照相同的標準評判學員的成績,因此,同一組內的學員成績可以做到公平公正。但由于每名老師的主觀評價標準不一樣,比如A 組的某老師將優秀的標準定為95分,B組的某老師則將優秀的標準定為85分。這樣一來一名優秀的學員選擇到A 組或是B 組答辯時,最終得到的答辯成績是不一樣的。我們將這種由于各組評委老師主觀評價標準的差異而導致的學員成績差異,稱之為組間差。
組間差導致了學員考核時的不公平,對于這種現象,一種常用的解決方案就是各組間統一評分標準。同時采用抽簽的方式,哪個學員進入哪個考場由自己抽簽決定,盡最大可能消除學員對評價不公正的抱怨。但統一評分標準的實施取決于評委老師的主觀意志,不好實現,抽簽方式也沒有從本質上消除組間差,需要一種更好的消除組間差的方法。下面我們從算法層面討論如何徹底消除組間差。
2 組間差消除算法
學員的答辯成績是一組單指標的數值型數據,對數值型數據進行度量的指標有兩個:一是分布的集中趨勢,反映各數據向數據總體中心值靠攏或聚集的程度。二是分布的離散趨勢,反映各數據遠離數據總體中心值的程度。學員答辯成績存在組間差的原因是每組評委的主觀評價標準不一致,反映到數據層面就是各組成績的集中趨勢和離散程度不一致。對一組數值型數據來說,其集中程度用平均數來度量,其離散趨勢用標準差或者方差來進行度量[2]。消除組間差的方法就是將各組數據同時進行標準化變換,具體方法是將各組數據同時減去平均分,并除以標準差。這種方法稱為Z-score 標準化方法,計算公式如下[1]:

其中,v為學員的原始分數,μi為i 組學員成績的均值,σi為i 組學員成績的標準差,v′為標準化后的學員成績。公式中采用標準差去度量數據的離散程度,而不采用方差,就是為了計算時保持與平均值同一量綱。采用式(1)經過標準化變換之后的各組分數平均數都為0,標準差都為1。這樣一來,各組成績的集中程度和離散趨勢就一致了,達到了消除各組成績組間差的目的。
采用式(1)進行標準化變換之后的成績雖然消除了各組成績之間的組間差,但是各組學員成績的平均值都是0,圍繞0 上下波動。學員辛苦學習了一年,最后得到的成績是0 分甚至是負分,這是很不合理的。因此我們需要將第一次標準化后的成績再變換一下,將成績再乘以總體學員成績的標準差,加上總體學員成績的平均值,其變換公式如下:

式(2)中,v″為標準化變換后的學員最終成績,v′是學員第一次標準化變換后的成績,公式中的σ是總體學員成績的標準差,而不是各組的標準差,μ是總體學員成績的平均值,不是各組的平均值。經過如此一變換,學員的成績就回到了合理的范圍之內,且所有學員成績的標準差和均值都一致了。
3 算法驗證實驗
下面我們以學院2019 年度某班次學員畢業設計答辯為例來對算法進行驗證。該班次學員學制1 年,全班共有42 名學員,答辯分3 個組同時進行,每一組14 名學員,學員的組別和答辯次序在答辯開始前通過程序隨機生成,因此理論上各組之間優秀學員的比率相差不大。每組安排7 名評委老師,學員的原始答辯成績為各評委評分成績相加,先減去一個最高分,再減去一個最低分,然后除以評分人數減2。學員原始答辯成績由式(3)計算后得出,yi為某評委為答辯學員打分成績,Y為當前答辯學員的得分集合。
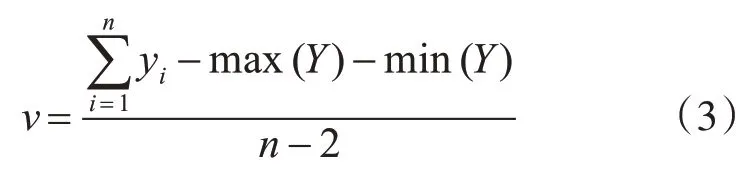
表1 為學員分組情況和通過式(3)算出的原始答辯成績。為保護學員的隱私,我們將學員的真實姓名隱去,分別以學員1、學員2……代替。

表1 2019年度XX班次學員畢業設計原始答辯成績表
計算得出,1 組學員的平均成績μ1為88.34,標準差σ1為5.79。2組學員的平均成績μ2為90.2,標準差σ2為4.98。3 組學員的平均成績μ3為89.87,標準差σ3為5.63。全體42 名學員總的平均成績為89.47,標準差為5.4。從學員的原始答辯成績我們基本可以看出,第1 組學員的平均成績最低,成績之間的標準差最大,代表學員水平之間的差異最大,學員平均成績低有兩個可能,第一是該組學員的水平確實很低,另外一種可能是該組答辯老師的評判標準過于嚴苛,下面通過對原始答辯成績進行標準化變換來驗證這兩種可能性。通過式(1)對學員的答辯成績進行標準化變換后,得到的成績如表2所示。通過式(2)對表2的成績再一次進行轉換,最后得到的學員標準成績如表3所示。
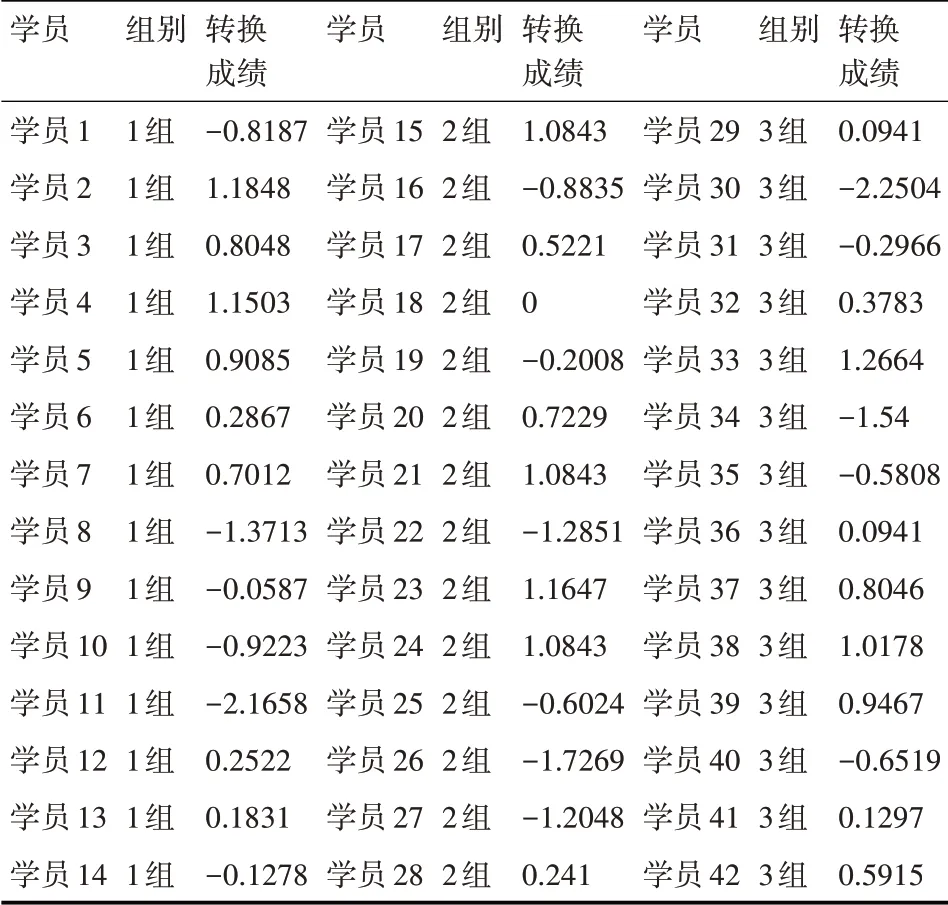
表2 第一次轉換后的成績
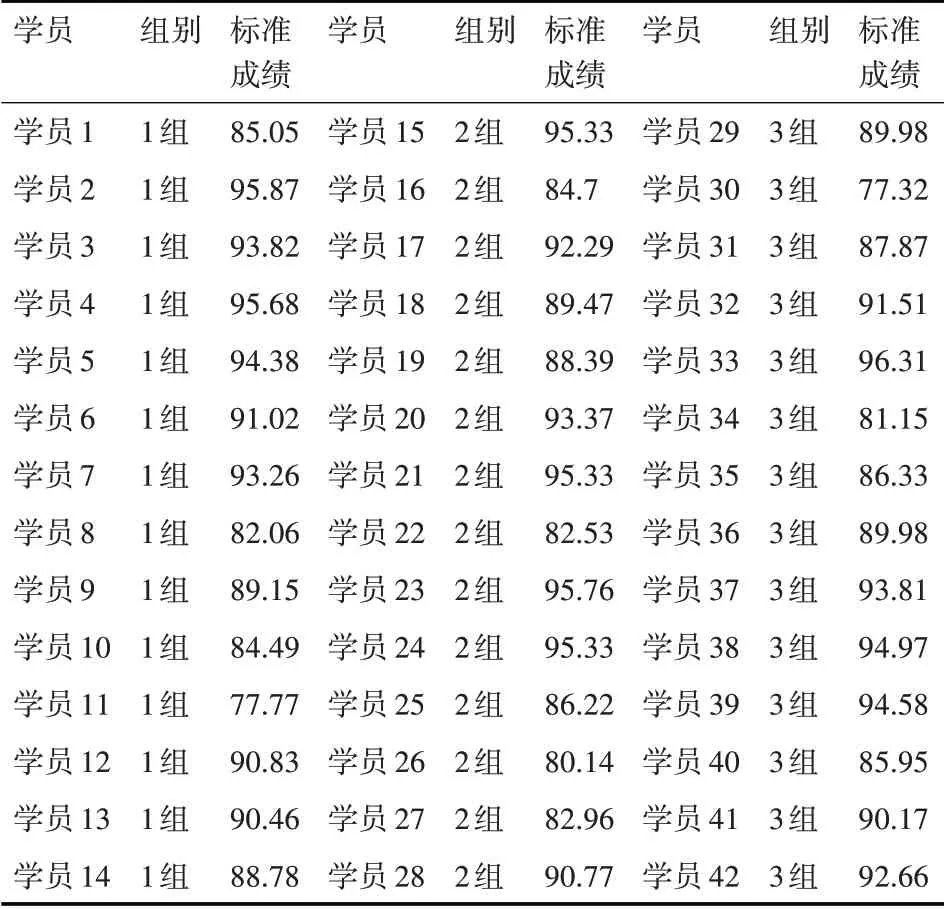
表3 2019年度XX班次學員畢業設計標準成績表
為了說明經過標準化處理之后的成績比原始答辯成績更為合理,我們將這兩份成績分別與專業理論考試成績進行比較,因為專業理論考試成績是筆試成績,相比答辯成績更為客觀,專業理論考試成績如表4 所示。我們分別計算原始答辯成績與專業理論考試成績的相關度,以及標準化后的答辯成績與專業理論考試成績的相關度,將兩個相關度進行比較。以專業理論考試成績為準繩,誰與其相關度更大,誰就更合理。
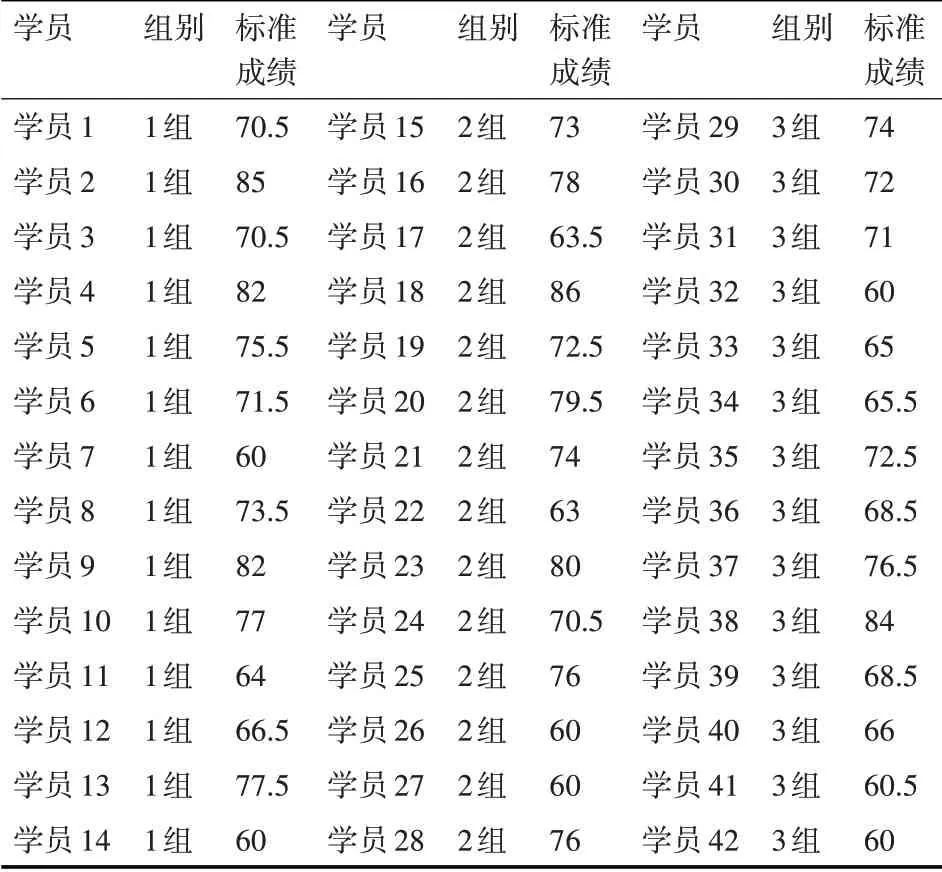
表4 2019年度XX班次學員專業理論考試成績表
通過計算,得出標準化后的答辯成績與專業理論考試成績的相關度為0.9611,原始答辯成績與專業理論考試成績的相關度為0.9541,兩者都是高度相關且非常接近。但標準化后的答辯成績與專業理論考試成績的相關度更高,說明經過標準化后的答辯成績更為合理。至于兩者數值非常接近的原因有兩個,首先,樣本數據量不足,學員只有42 個,分成3 組。其次,為了盡量保持客觀公正,事先制定了統一的答辯評分標準并召集全體評委開會,要求3 組評委按評分標準統一執行,最大限度地保證了原始答辯成績的客觀公正。
將表1 中的原始答辯成績按成績由高到低排序,取前10 名,得到表5。將表3 中的經過標準化處理后的成績由高到低排序,取前10名,得到表6。
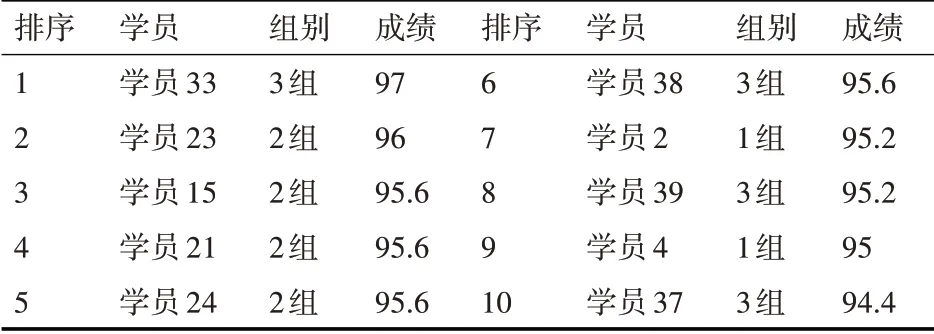
表5 學員畢業設計原始答辯成績前10名情況
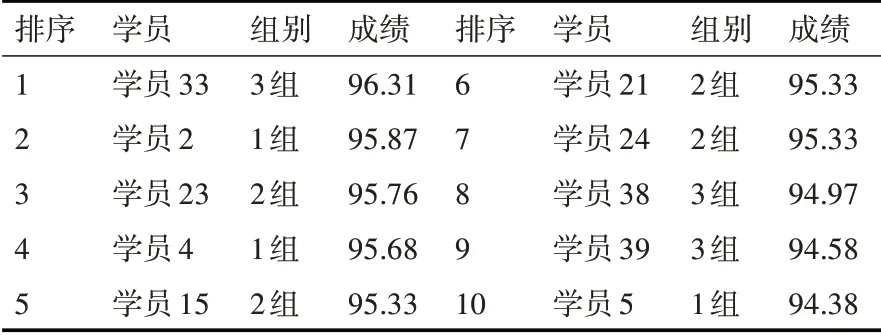
表6 學員畢業設計標準化答辯成績前10名情況
通過比較表5和表6,不難發現如下幾個規律:首先,兩個表中學員的重合率高達80%,也就是說對兩種成績分別取前10 名,有8 名學員是重合的,這符合客觀規律,因為優秀的學員不管怎么排序,始終是優秀的,如學員33 在兩種排名中都是處于第一名的位置;第二,雖然兩個表的學員重合率高達80%,但排名會發生變化。其中第1 組的學員排名變化最大,在原始的答辯成績排名中,第1 組學員只有2 人進入前10 名,且排名相對靠后,分別為學員2,排名第7,學員4,排名第9。經過標準化處理后,學員2 由第7 名上升到了第2 名,學員4 由第9名上升到了第4名,并且第1組的學員5原來在10名之外,成績經過標準化處理之后,上升為第10名。這說明與其它兩組評委相比,第1 組的評委老師評分標準過于嚴苛。另外經過標準化處理后,第3 組的學員37 退出了前10 名,第38 名和第39 名的名次都后退了1 至2 個名次,說明第3 組的評判相對較為寬松。第2組的4名學員在兩個表中都進入了前10,說明該組的評判最為公正,這4 名學員在表6中的排名較表5退后了1到2位,說明該組的評判較第1 組寬松;第三,在表5 和表6 中,第2 組的4位學員的成績都出現了很大的重合,沒有拉開名次之間的差別,這一點我們在計算答辯成績的標準差時就可看出,第二組答辯成績的標準差σ2為4.98,是3 組中最小的,這說明該組成績的離散程度最小,評委老師沒有充分將成績距離拉開。
4 結語
答辯是常用的一種考核方式,在院校和企事業單位都用得很多,當參加面試的人數過多時,通常采用分組答辯的方式進行。為了公平起見,答辯主辦方一般會采用抽簽,各組間統一評分標準等方法來盡量消除各組評分之間的差異。但由于如何執行評分標準取決于評委的閱歷和知識背景等因素,主觀性較強,因此無法完全消除各組評分之間的組間差,所以必須引入算法才能消除各組評分的組間差,實現完全的公平公正。本文引入Z-Score 數據處理標準化方法并對其進行了改進,將各組原始答辯成績經過兩次標準化變換后,最終去除了各組成績之間的組間差。該方法消除了分組答辯中由于各組評委主觀評分標準不一致而出現的答辯成績組間差,且操作簡單,在學員的考核、面試、招生等活動中具有現實意義。

