基于計算聽覺場景分析的單通道語音分離方法*

徐慶達 張二華

（南京理工大學計算機科學與工程學院 南京 210094）

1 引言

語音作為人機交互的主要方式之一，在語音識別系統、說話人識別系統等中得到廣泛應用。但實際環境和理想環境存在很大差異，語音信號中往往存在“未知”的干擾，如音樂、汽車鳴笛、動物叫聲等。這些干擾很大程度上影響了語音信號分析系統的性能，如何消除噪聲并獲得純凈的語音信號成為語音技術發展的關鍵技術之一。

經研究表明，人耳有較強的語音分析能力，在復雜場景下即使只用一只耳朵，也能排除噪聲干擾，有選擇的聽取所需內容［1］。1953年英國科學家Cherry將該現象稱為“雞尾酒會”問題［2］。之后人們對于人耳聽覺系統的研究經歷了較長時間，Bregman 經過多年的研究，在20 世紀90 年代發表《聽覺場景分析》（Auditory Scene Analysis，ASA），聽覺場景分析是從人的聽覺生理以及心理特征出發，研究人耳在聽覺感知過程中的機理［3~4］。

2004 年，Guoning Hu 和Deliang Wang 提出了著名的Hu-Wang 模型，該模型采用基音特性和幅度調制特性分別處理低頻和高頻區域，分離結果的高頻區域得到了改善，分離效果得到了提高［5~6］。2010 年，Guoning Hu 和Deliang Wang 提出了用于基音估計和濁音分離的算法，即tandem 算法，該算法迭代的進行基音估計和二值模估計，可以準確地獲得基音和目標語音的二值模［7~8］。2013年，基于tan-dem 算法，Guoning Hu 和Deliang Wang 提出了一種無監督的語音分離系統，該算法在完成濁音分離后，通過多尺度Onset/Offset 分析產生待分離清音段，并利用已分離的濁音的二值模來組織清音段，實現清音分離［9］。

本文首先分析了語音信號的頻域特征，語音信號在濁音部分其頻譜分布具有明顯的諧波特性，在倒譜域上有明顯的峰值，由倒譜峰值的位置可以推算出基音周期。本文以語音信號的短時平穩性和基音周期的連續性等作為語音分離的線索，在求取基音頻率后采用梳狀濾波提取各次諧波的頻譜，再進行傅里葉逆變換得到分離后的語音，實驗證明了該方法的有效性。

2 CASA概述

人耳聽覺系統對聲音的感知主要分為兩個階段，即分解和組合。人耳會將聽到的聲音分解成不同的感知單元，這些感知單元來自不同的發聲源，然后，聽覺系統會將來自同一發聲源的感知單元重新組合到一起，形成能夠表達一定內容的語音片段［10］。其中組合分為“時序組合”和“同時組合”，如圖1 所示，B 和C 屬于同一時間不同頻段的感知單元，兩者的組合屬于“同時組合”，A 和B 屬于同一頻段不同時間的感知單元，兩者按時間的先后順序的組合屬于“時序組合”。計算聽覺場景分析正是用計算機來模擬人耳的聽覺系統，并建立相應的語音信號分離模型。

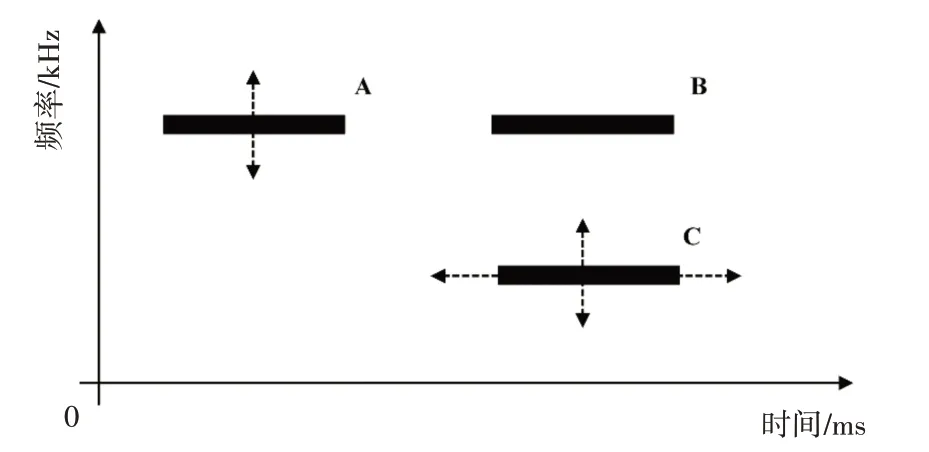
圖1 同時組合與時序組合

3 語音信號的特征分析

本文主要使用短時傅里葉分析方法對語音信號的短時譜和語譜圖進行研究。通常取10ms~30ms為一幀，第n幀語音信號xn(m)的短時傅里葉變換的定義如式（1），w(n-m)為窗函數。

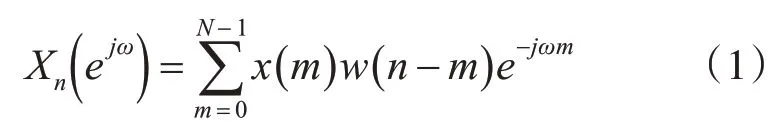
為了將時域信息與頻域信息相互結合，便于系統的分解和組合，可將連續幀的頻譜曲線按時間先后“豎”向繪制，再把頻率分量在某時間點上的幅值轉換為像素灰度值，以此為依據來繪制語譜圖。語譜圖的繪制過程如下。

1）對輸入的語音信號進行短時傅里葉變換，對得到的實部和虛部的平方和開根號，得到振幅譜v={s1，s2，…，sn} ，其中v為二維數組，n為幀號，sn代表第n幀的振幅譜數據。

2）將所有振幅譜數據按照數值大小升序排序，以20 百分位處的數值為低截止閾值smin，80 百分位處的數值為高截止閾值smax，高于smax的像素值為0，即黑色，低于smin的像素值為255，即白色，其余的振幅映射到0~255之間。

圖2 給出了純凈語音某男聲漢語“那年”的波形圖及其語譜圖，其中幀長為512 個采樣點，采樣頻率為16kHz，即每16000 個采樣點代表1s。觀察發現濁音段濁音區域一條條橫向的條紋，也就是諧波系結構，這些諧波包含了語音信號中的主要信息，各次諧波的位置將作為語音分離的主要線索。

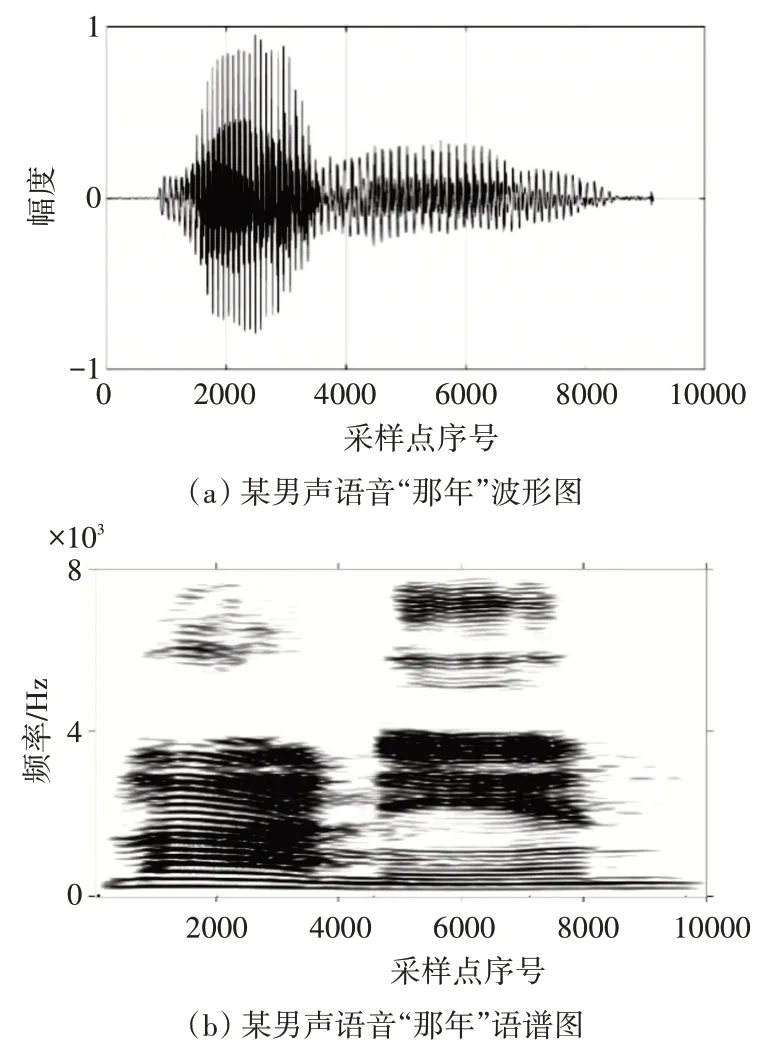
圖2 某男聲語音“那年”波形圖與語譜圖

4 基音周期的提取

語音產生的過程可以通過激勵源和濾波器模型模擬，激勵源代表聲帶振動，濾波器代表聲道，兩者在時域通過卷積計算得到語言信號。對語音信號利用倒譜解卷原理，可以得出激勵序列的倒譜，倒譜峰反映了基音信息，所以據此可以計算出基音周期［11~12］。

4.1 基于倒譜法的基音周期提取

首先按第3 節中的式（1）對第n幀語音信號xn(m)進行短時傅里葉變換得到短時譜Xn(ejω)，短時譜Xn(ejω)包含實部和虛部，設

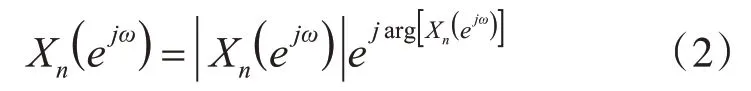
對其取對數得

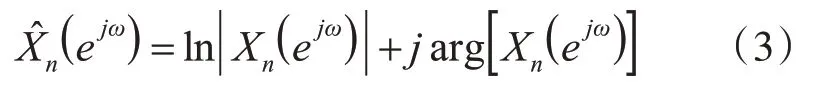
再對實部ln|Xn(ejω)|做傅里葉逆變換可得到倒譜c(n)，如式（4）：

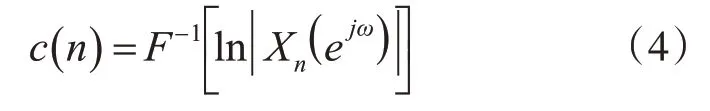
圖3（a）為語音信號對數振幅譜ln|Xn(ejω)|示意圖，虛線對應于頻譜包絡的慢變化分量，實線對應于諧波的快變化分量，諧波的變化頻率就是基音頻率。將對數振幅譜做傅里葉逆變換，即可將慢變化分量與快變化分量分離開［13］。圖3（b）為倒譜c(n)的示意圖，橫軸表示倒譜頻率，量綱是時間，其中靠近原點的低倒頻部分是頻譜包絡的變換，位于t0處的有明顯的峰值，t0對應的時間就是基音周期。

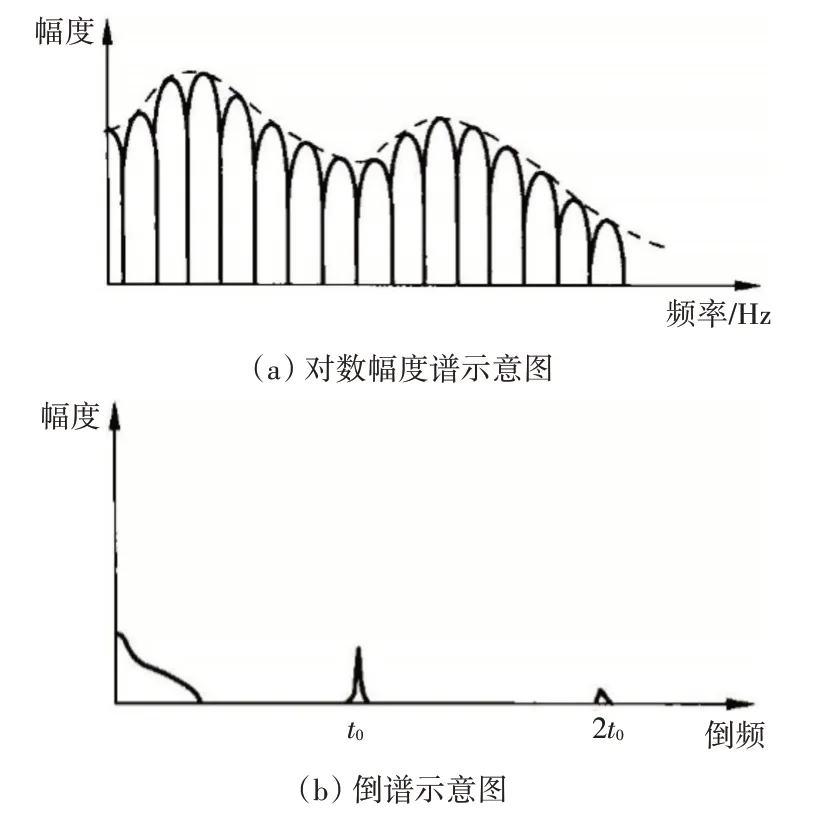
圖3 倒譜示意圖

設信號采樣頻率為f，則時間采樣間隔為Δt=1f，若幀長為M，某一幀的倒譜數據為c(M)，若其在第l個樣點序號處產生明顯的峰值，則基音周期Tp為

基音頻率fp定義如式（6）：

4.2 基音周期軌跡的繪制

語音信號具有短時平穩性，且是漸變的，屬于同一聲源的基音周期具有一定的連續性。本文以每幀的倒譜數據為依據，將相鄰幀的倒譜數據按一定的映射規則轉換為像素灰度值，然后在垂直方向上繪制出各幀倒譜的灰度值。其繪制過程與語譜圖類似，圖4（a）為某男聲“那年正月新春”純凈語音波形圖，圖4（b）為其基音周期軌跡圖。基音周期軌跡圖中的縱坐標為時間，因采樣率為16kHz，即單位Δt=1 16000s。

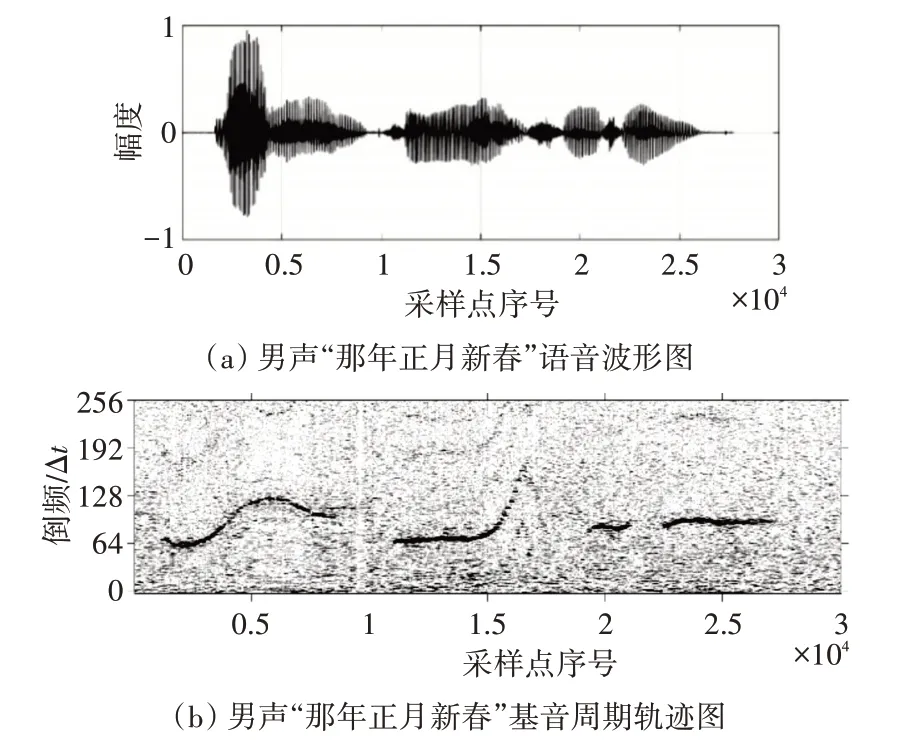
圖4 語音波形圖和基音周期軌跡圖

5 語音分離

5.1 諧波提取

在第4 節中已經給出了基音頻率確定的方法，而各次諧波的頻率fh為基音頻率fp的整數倍，即fh=k×fp，按基音頻率的整數倍提取各次諧波可得到需要的頻譜數據。由于基音頻率的計算會產生很小的誤差，在高頻部分當k較大時誤差會被放大，本文使用迭代更新第k-1 次諧波位置的方法來確定第k次諧波位置，以此提取各次諧波，縮小了高頻部分的誤差，提高了諧波提取的準確性。

設信號采樣頻率為f，某段語音的振幅譜數據為v={s1，s2，…，sn} ，幀長為N，某一幀的振幅譜數據sn的長度為N，對應于N個點序號，則頻率采樣間隔Δf=f/N，由4.1 節中式（6）得基音頻率fp=f/l，則某一幀的一次諧波位置點序號i1=int(fp/Δf)=int(N/l)。

諧波提取過程如下：

1）將語譜圖中灰度值85 對應的振幅作為各次諧波的振幅閾值AH。

2）根據基音頻率fp設置諧波搜索范圍（R表示要搜索的樣點的范圍），避免相鄰兩個諧波位置的交叉。

3）根據基音頻率fp確定一次諧波的理論位置i1=int(N/l) ，對i1四 舍 五 入 取 整，并 搜 索[i1-R，i1+R] 范圍內的極大值，若找到局部極大值A(ix)，且A(ix)≥AH，則本次諧波頻率點位置就為ix，更新i1=ix；否則舍去該次諧波頻率點，i1=int(N/l)不做更新。

4）經過步驟3）在一次諧波確定的情況下，從第二次諧波開始，以ik=ik-1+i1依次求取剩余各次諧波，ik的更新與確定與步驟3）一致。

圖5（a）為純凈語音某男聲“那年正月新春”語譜圖，圖5（b）為其按上述方法提取的諧波結構圖。

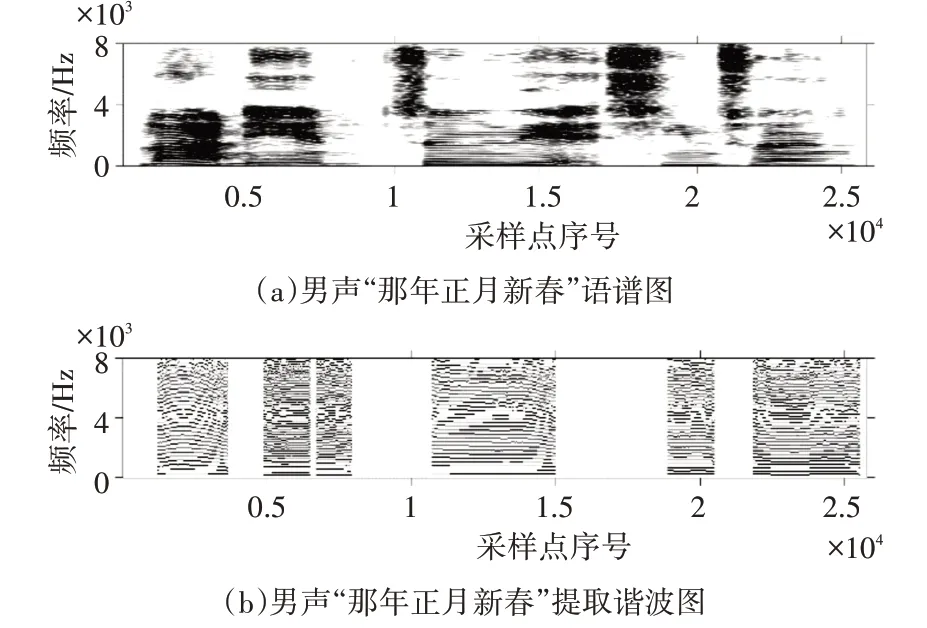
圖5 某男聲“那年正月新春”語譜圖與諧波提取圖

5.2 語音重構

對于提取完諧波的單幀頻譜進行傅里葉逆變換可得到分離后的單幀語音信號［14］。短時傅里葉變換是將時域信號轉換到頻域，而短時傅里葉逆變換 則 是 將 頻 域 信 號Xn(ejω)恢 復 為 時 域 信 號x(m)。第3節中式（1）對應的傅里葉逆變換公式為

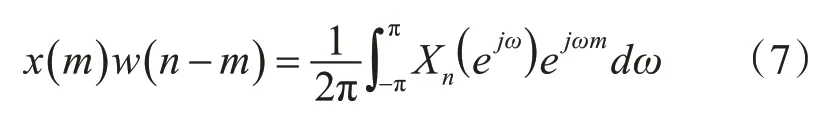
令m=n，且w( 0 )≠0 時，有

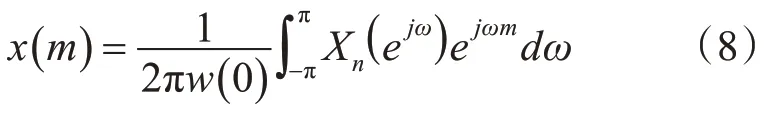
對于分離后的單幀語音信號，由于相鄰幀之間在時域上有重合，因此，在同一段基音軌跡對應的時間范圍內，將各語音幀按照間隔幀移大小的距離進行對齊。如圖6，對于重合部分采用疊加求均值的方式來重構語音信號，可得到分離后的語音。

圖6給出了語音重構的過程示意圖。

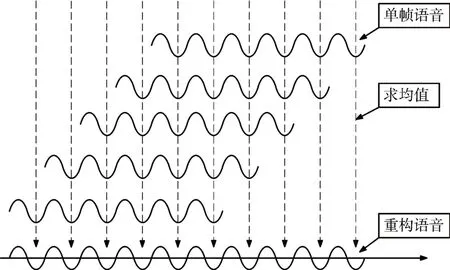
圖6 語音重構過程示意圖

6 實驗結果

本實驗將原始語音某男聲“那年正月新春”與不同噪聲混合后做分離試驗，選取的噪聲分別為電話按鍵聲、白噪聲、流水聲、水中氣泡聲、鳥叫聲，圖7為五種噪聲的波形圖。

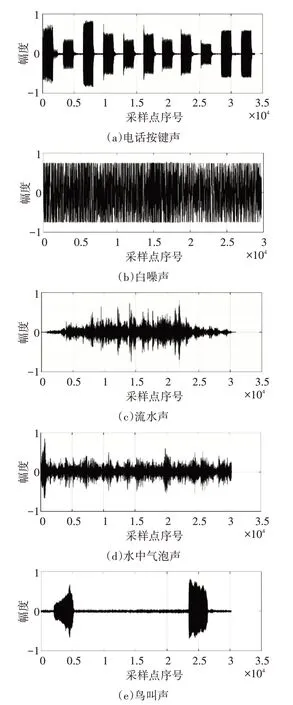
圖7 五種噪音的波形

本實驗將原始語音與噪音按一定的信噪比（SNR）進行混合，對混合語音進行分離試驗，其中信噪比設為5。信噪比（SNR）計算公式如式（9），其中，x(m)為原始語音信號，v(m)為噪音信號。

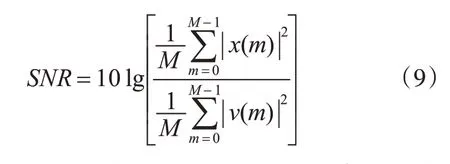
圖8~圖12為原始語音與五種噪音混合后的波形以及分離后的語音波形圖。

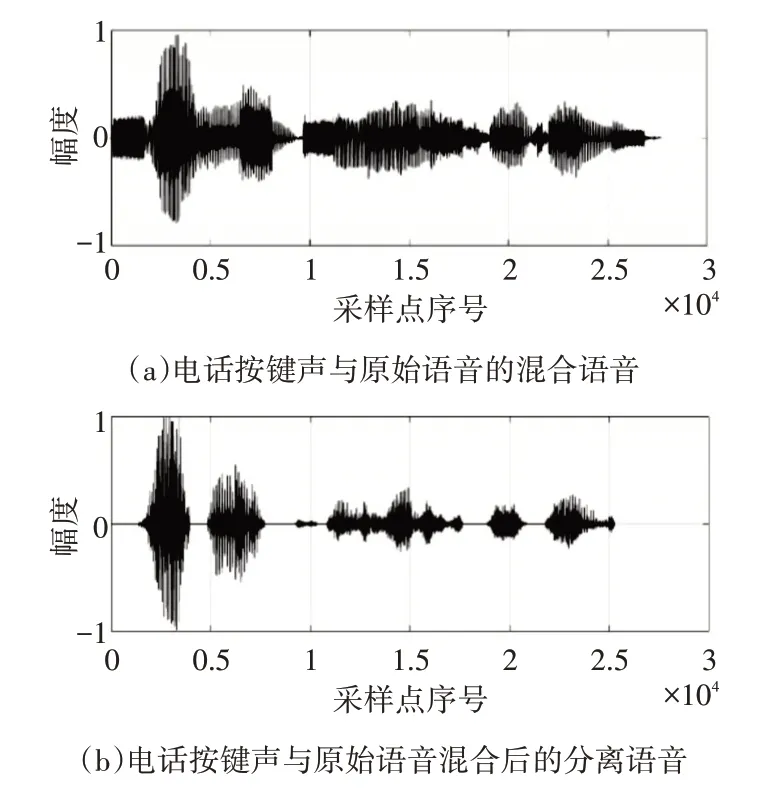
圖8 電話按鍵聲與原始語音的混合與分離

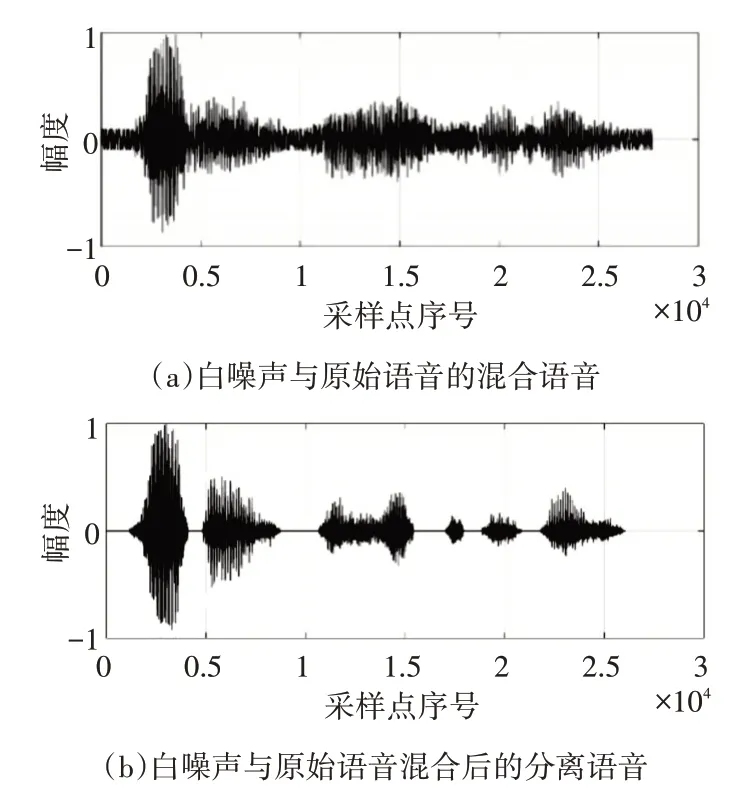
圖9 白噪聲與原始語音的混合與分離

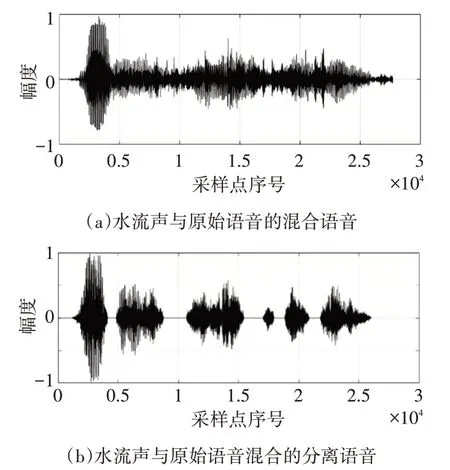
圖10 水流聲與原始語音的混合與分離

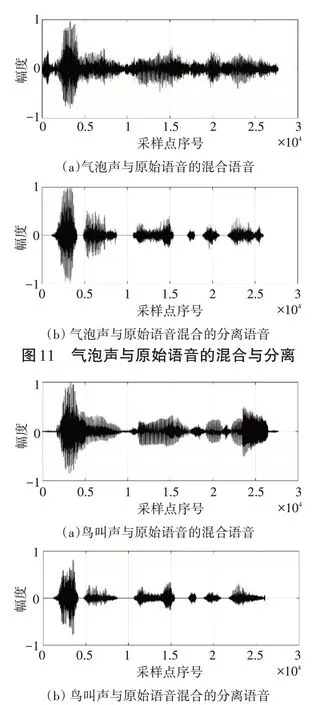
圖12 鳥叫聲與原始語音的混合與分離

本文主要采用主觀評價的評價意見分（Mean Opinion Score，MOS）和信噪比SNR 來對實驗結果進行評估［15］，MOS評估標準如表1所示。本文對參與本實驗評估的60 個人的MOS 分值取均值，得出最后的分數。分離語音的信噪比SNR 的計算公式如式（10），其中x?(m)為分離后的語音信號，x(m)為原始信號。

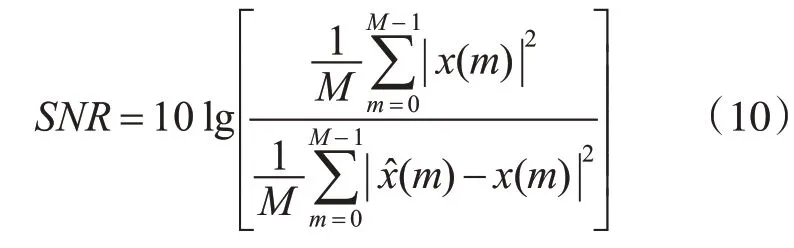
表1 MOS值評分標準

上述實驗中將五種噪聲與原始語音按一定信噪比混合然后進行分離實驗，表2 給出了分離前后的MOS評分和信噪比SNR的對比。

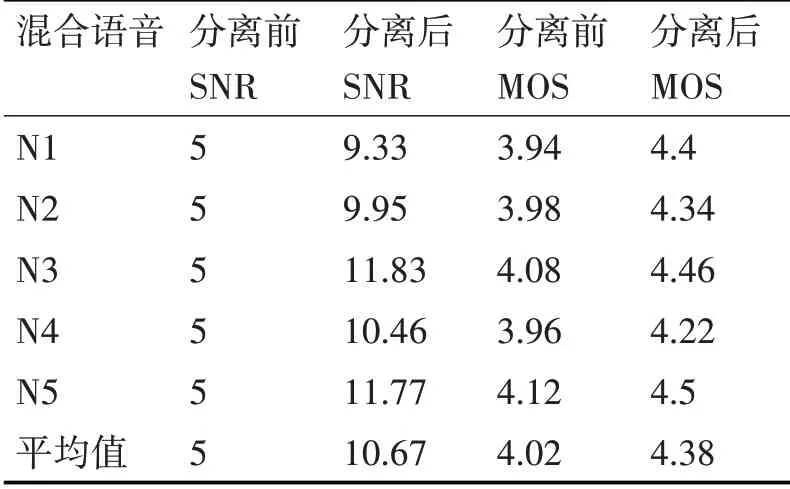
表2 分離前后評估表

從分離后的語音波形圖和表2 中的數據可以看出，經過分離處理后的語音質量得到了明顯的改善，噪音得到大幅度的消減，且聽覺效果得到較好的改善。但當噪音干擾過強，人耳已經難以分辨時，分離的效果并不是很好，關于強噪音下的語音分離還有待改善和研究。

7 結語

本文介紹了計算聽覺場景分析的原理和基于該原理的語音分離方法。該方法中較為重要的步驟是基音周期的提取，本文采用倒譜法來確定基音周期，后根據基音周期確定濁音段語音信號頻譜上的諧波位置，對提取的頻譜做反變換重構原信號。實驗表明，該方法可有效提高語音信號的信噪比和可讀性。