基于小波分解的鼾音信號功率譜估計方法研究*
劉 勇 袁立飛 袁麗峰
(河北省眼科醫院 邢臺 054000)
1 引言
OSAHS 病人的阻塞位置需要經睡眠呼吸監測結合纖維喉鏡檢查、影像學檢查才能確定,成本高且需要在醫院才能進行,打鼾是OSAHS 病人的典型癥狀,研究不同阻塞位置鼾音的功率譜估計[1]特點,為診斷OSAHS 阻塞位置提供一種簡單方便的檢測方法。功率譜估計方法分為傳統譜估計法[2]和現代譜估計法[3]。傳統譜估計法原理簡單,便于實現,在實際中應用較廣,常用的方法有Welch法[4~6]、多窗譜法[7~8]等。現代譜估計是先將實驗信號建立參數模型,再依據模型估計信號的功率譜。線性模型在信號處理中應用最多,具體分為AR 模型[9]、MA模型、ARMA模型。常用的方法有基于AR模型的自相關法[10]和Burg 法[11]。分析鼾音和阻塞位置的不同功率譜估計特點,為診斷OSAHS 阻塞位置提供幫助。
針對上述問題,提出了基于小波分解的鼾音功率譜估計方法,首先將鼾音信號進行小波分解[12~14],子帶信號代表鼾音信號的不同時頻域信息,對各子帶信號分別采用Welch法、多窗譜法、基于AR 模型的自相關法和Burg 法。結果表明,基于小波分解的Welch 法得到的鼾音功率譜估計結果分辨率和方差可以滿足需要,同時初步分析了上部阻塞和下部阻塞功率譜估計特征。
2 小波分解原理
設ψ(t)∈L2(R) ,傅里葉變換表示ψ?(ω) 。當時,ψ(t)表示母小波。小波序列是指ψ(t)伸縮、平移所得的序列。
離散小波序列為
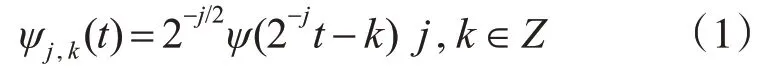
對于二進離散小波變換,信號{X(t)} 通過小波函數ψj,k(t),尺度函數φj,k(t)進行J層分解:
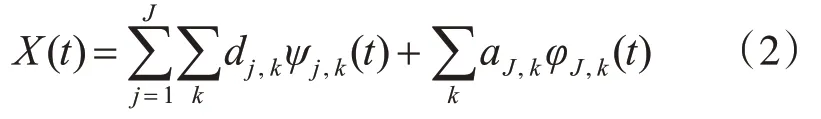
dj,k為尺度j上的細節信息,稱為小波系數;aJ,k為尺度J上的逼近信息,為近似系數。
選擇不同的尺度,其時頻分辨率不同,小波分解存在逆變換,將小波系數和近似系數重構[15],可得到信號中的不同頻率成分。
3 鼾音功率譜估計方法
3.1 Welch法
Welch 法是將整個信號分段處理,相鄰的每段進行重疊,然后對數據加窗進行譜估計,是周期圖法的改進。
主要步驟如下:
1)將數據xN(n) 分成L段,每段數據長度為M,即N=LM。對xN(n)分段時,假設50%重疊,則第i段數據表示:
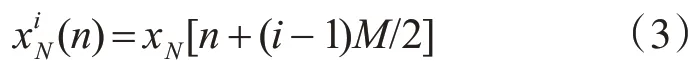
2)對每段數據加窗w(n)傅里葉變換,表示為
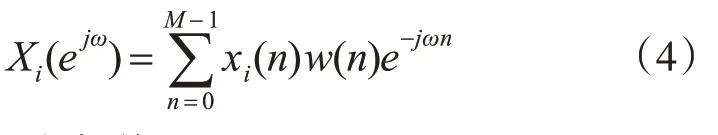
3)求分段功率譜:
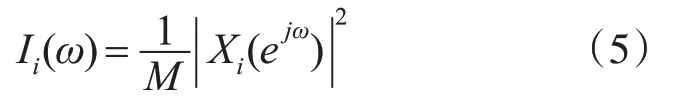
4)求平均功率譜:
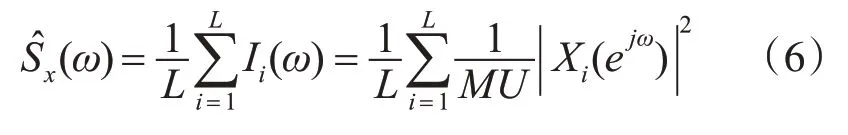
通過分段重疊和加窗的方法,譜估計結果是逐步一致估計,并且可以減少方差。窗函數是Welch法的關鍵因素,為提高分辨率和減小譜泄漏,理想是選擇旁瓣幅值小,主瓣寬度小的窗函數,但是實際中兩者不能同時小,需要根據信號特點和實際情況,選擇合適的窗函數。
3.2 多窗譜法
多窗譜法是對信號采用多個互相正交的窗函數,然后進行傅里葉變換,最后得到信號的譜估計。
設時間序列為x(1),…,x(N),S(f)為真實譜。存在K個互相正交的數據窗,{ }ht,k:t1,…,N代表第k個窗,K個直接譜的均值為該序列的多窗譜Smt(f)。表示為
其中Smt(f)是對數據加第k個窗的直接譜。表示為
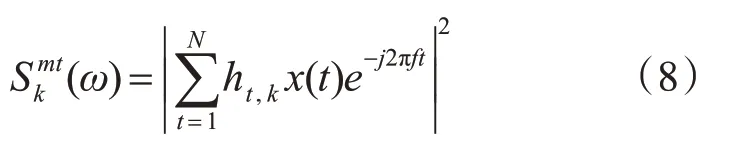
多正弦窗,即正交窗和最小偏差窗的集合。對于正弦窗:
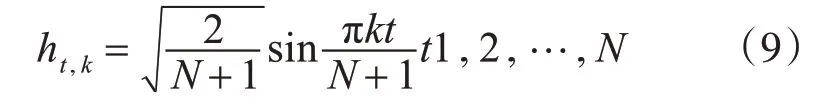
多正弦窗主瓣窄,分析式簡單,就有較低的偏差。
為防止譜泄漏,采用一組相互正交的數據窗代替單個數據窗,這樣可以利用信號兩端的數據,進而減小方差,提升譜估計性能。
3.3 AR模型功率譜估計
原理是現在的輸入和過去p個輸出的加權之和表示該模型現在的輸出。
對于p階AR模型,有
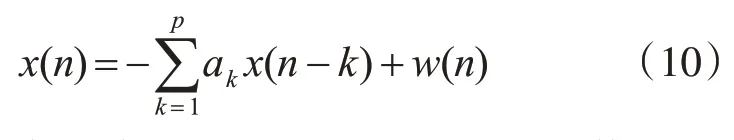
其中w(n)為白噪聲;a1,a2,…ap為p階AR 模型的參數。
該AR模型系統的傳遞參數為
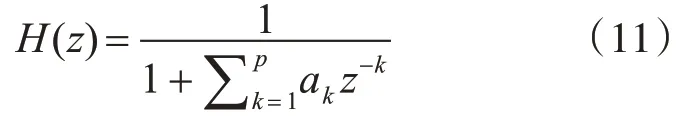
x(n)的功率譜為
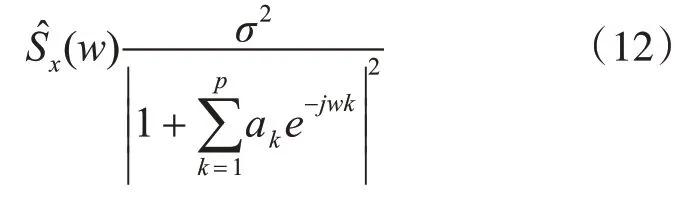
AR模型是全極點的模型。平穩信號可以通過AR模型表示,AR模型計算簡單,是最常用的模型,在語音信號處理等領域應用廣泛。
3.3.1 自相關法
自相關法先估計自相關序列,然后通過萊文森遞歸公式算出AR系數,計算出功率譜。
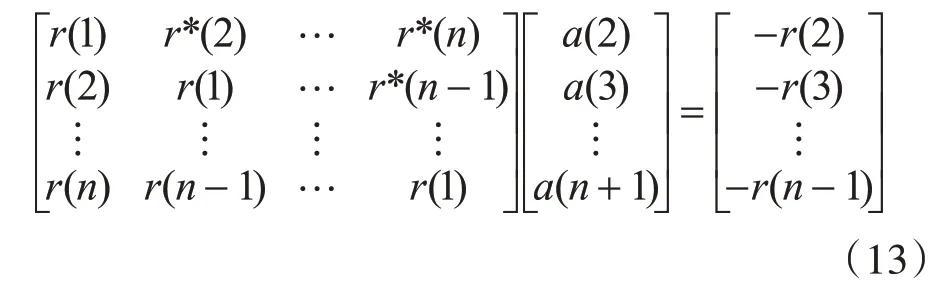
式中,r(1),r(2),…,r(n+1) 為相 關系數,a(2),…,a(n+1)為自回歸系數。
自相關算法功率譜公式為
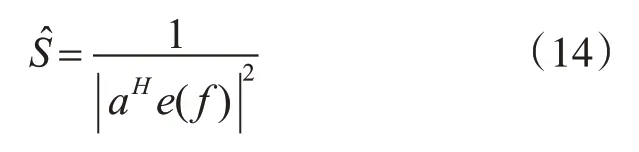
式中,e(f)為負數正弦曲線。
萊文森遞推是從低到高直到p階,p階之前的參數都會求出,可以尋找合適的階數,自相關法相當于加窗處理,短數據分辨率低。
3.3.2 Burg法
Burg 法是選擇反射系數使得前向和后向總的均方誤差的和最小,然后通過萊文森遞推算法算出模型系數。
數據x(1),…,x(N),前向預測誤差表示:
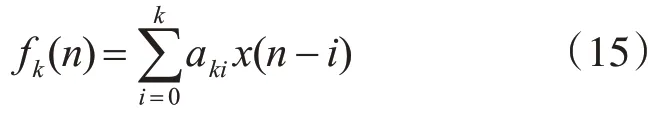
后向預測誤差表示:
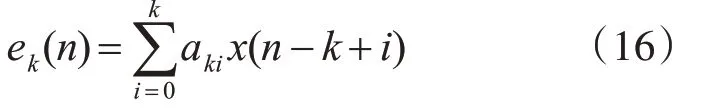
各階前向和后向預測誤差為
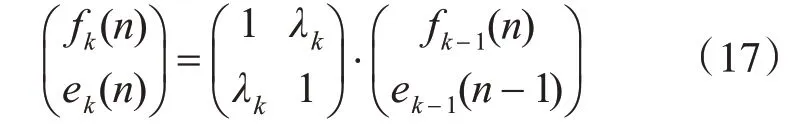
前向和后向預測誤差的平均功率為
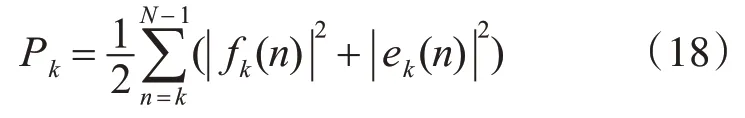
為使Pk最小,令?Pk?λk=0 ,得到反射系數為
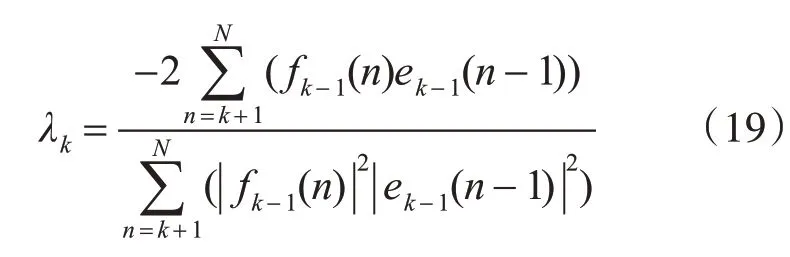
利用萊文森遞歸公式求解AR模型的參數為
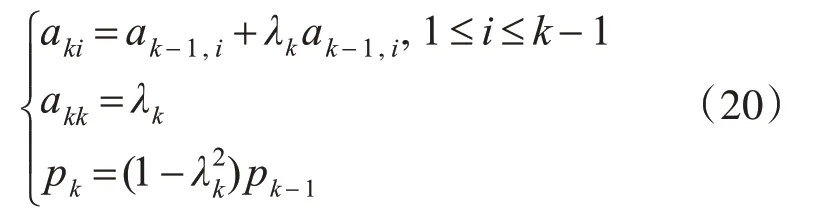
Burg 法中階次的選擇影響譜估計的質量,階次越高,頻率分辨率越高,但是容易產生譜線開裂和譜峰偏差的問題,同時對于低噪正弦信號敏感。
4 基于小波分解的鼾音譜估計
小波分解可以把采集到鼾音信號投影到小波基函數的空間中,將指定尺度上的小波系數和近似系數重構鼾音信號,可獲得對應的頻率子帶信號。將鼾音信號小波分解,提取相應的子帶實現鼾音的時頻域精細化分析,對不同子帶信號進行功率譜估計。
主要步驟如下:
1)將鼾音信號分幀處理。類似于語言信號,將10ms~30ms鼾音信號看作是相對平穩信號。
2)對每幀的鼾音信號進行小波4 層分解,選取3、4 層的小波系數重構,分離出相應的頻率成分,子帶信號表示為S1、S2 、S3,對應的頻率為0~1000Hz,1000Hz~2000Hz,2000Hz~4000Hz。
3)對子帶信號采用Welch 法、多窗譜法、自相關法、Burg法進行功率譜估計得到各子帶鼾音信號的功率譜估計。
5 實驗與分析
采集河北省眼科醫院150 名OSAHS 病人的鼾音信息,電容麥克風位于病人口部上方15cm 處,采集的音頻為WAV 格式,采樣頻率為32000Hz,精度為16Bit。
抽取一次鼾音信號作為數據樣本進行仿真實驗。對鼾音信號分幀,幀長為1024,根據鼾音信號的特點,采用dB4 小波基,對鼾音信號進行小波4層分解,對第1 個子帶鼾音信號S1 分別采用Welch法、多窗譜法、自相關法、Burg 法進行功率譜估計。Welch法中采用Blackman窗和Hamming窗,窗長為1024,段重疊為512,FFT長度為1024。多窗譜法中采用多正弦窗,時間帶寬積為2 和4。自相關法中階數為80 和300。Burg 法中階數為80 和300。子帶信號S1 的不同功率譜估計結果分別圖1、圖2、圖3、圖4所示。
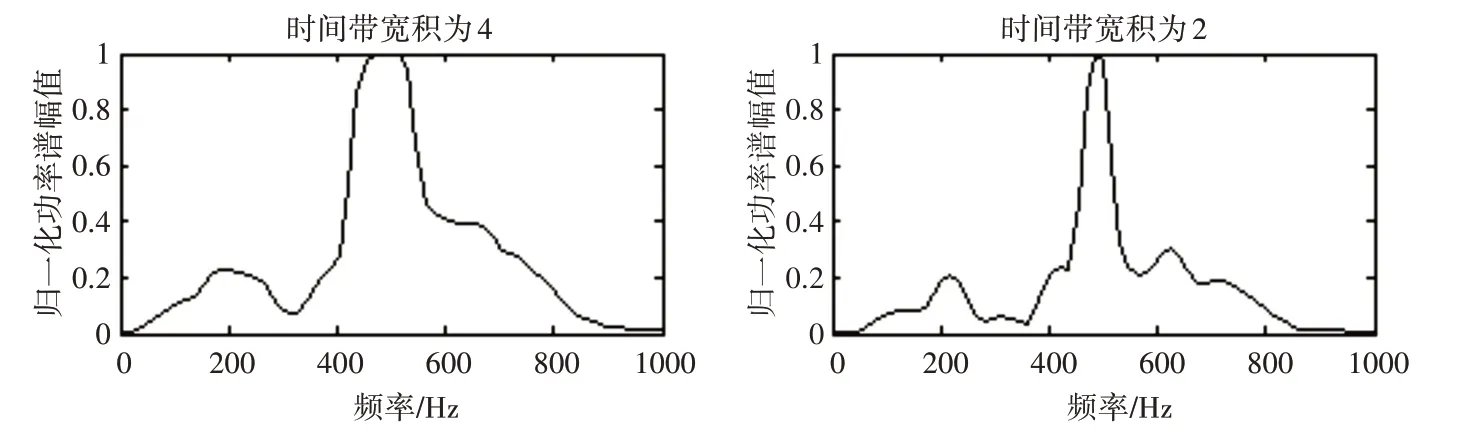
圖2 多窗譜法功率譜估計圖
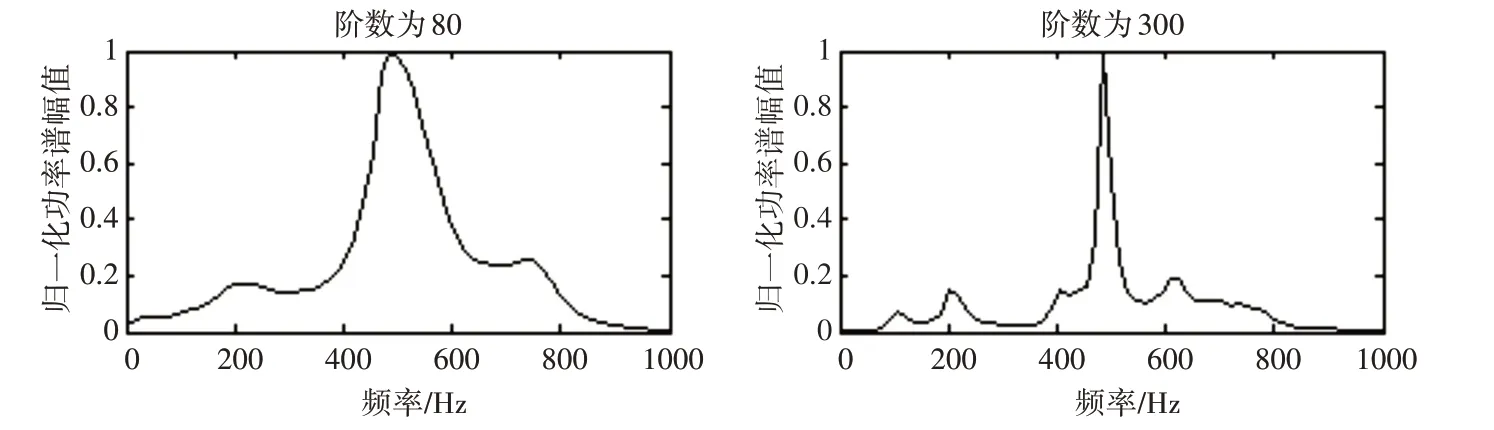
圖3 自相關法功率譜估計圖
圖4 Burg法功率譜估計圖
對于子帶信號S1,不同功率譜估計方法的方差如表1所示。
從圖1~4、表1可知:
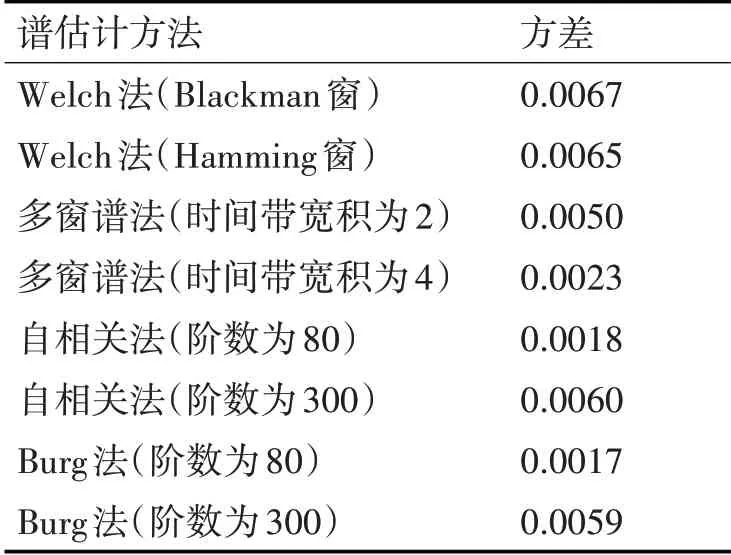
表1 不同鼾音功率譜估計方法的方差
圖1 Welch法功率譜估計圖
1)Welch 法 中Hamming 窗 的 頻 率 分 辨 率 比Blackman窗高,而且方差更小。窗函數的選擇至關重要,由于Hamming 窗的主瓣寬度更小,因此具有更好的分辨率性能。
2)多窗譜法中時間帶寬積等于2比等于4時分辨率高,方差增大。隨著時間帶寬積增大,窗的數目會增多,導致頻率分辨率降低,時間分辨率增加,同時譜泄露會增加。
3)自相關法和Burg 法性能非常接近,需要提高階次才能提高分辨率,階數越高有更多的譜細節,譜峰信息比較尖銳,其余地方比較平滑,但是高階次容易導致譜峰偏移。
4)從整體來看,分辨率方面,采用Hamming 窗Welch 法分辨率最高,其次是采用Blackman 窗Welch法,然后是階數為300的自相關法和Burg法,最后是時間帶寬積為2 的多窗譜法;方差方面,在分辨率相對高的情況下,方差由大到小依次為采用Blackman 窗Welch 法、采用Hamming 窗Welch 法、階數為300 的自相關法、階數為300 的Burg 法、時間帶寬積為2的多窗譜法。
5)綜上所述,采用hamming 窗Welch 法對鼾音的功率譜估計性能最好,分辨率和方差可以滿足需要。
鼾音是睡眠時呼吸道產生的聲音,沒有標準的數字模型,只能借助語音信號[16]的功率譜估計方法。在語音處理領域Welch 法是最常用的功率譜估計方法,從結果上看依然適用于鼾音信號功率譜估計;多窗譜法適合短數據、頻譜波動大的信號,如地震監測等,在鼾音領域不如Welch 法;AR 模型是全極點模型,鼾音信號類似于語音信號,有極點和零點。 基于AR 模型的自相關法和Burg 法結果是傳統譜估計的包絡線,階數越高有更多得譜細節,更重視譜峰信息,其余地方比較平滑。
臨床上不同的阻塞位置采用不同的手術方法,分析上部阻塞和下部阻塞的功率譜特性來判斷阻塞位置。根據上述結論小波分解的基礎上選擇Welch法,對3個子帶信號進行功率譜估計,上部阻塞和下部阻塞功率譜估計結果如圖5所示。
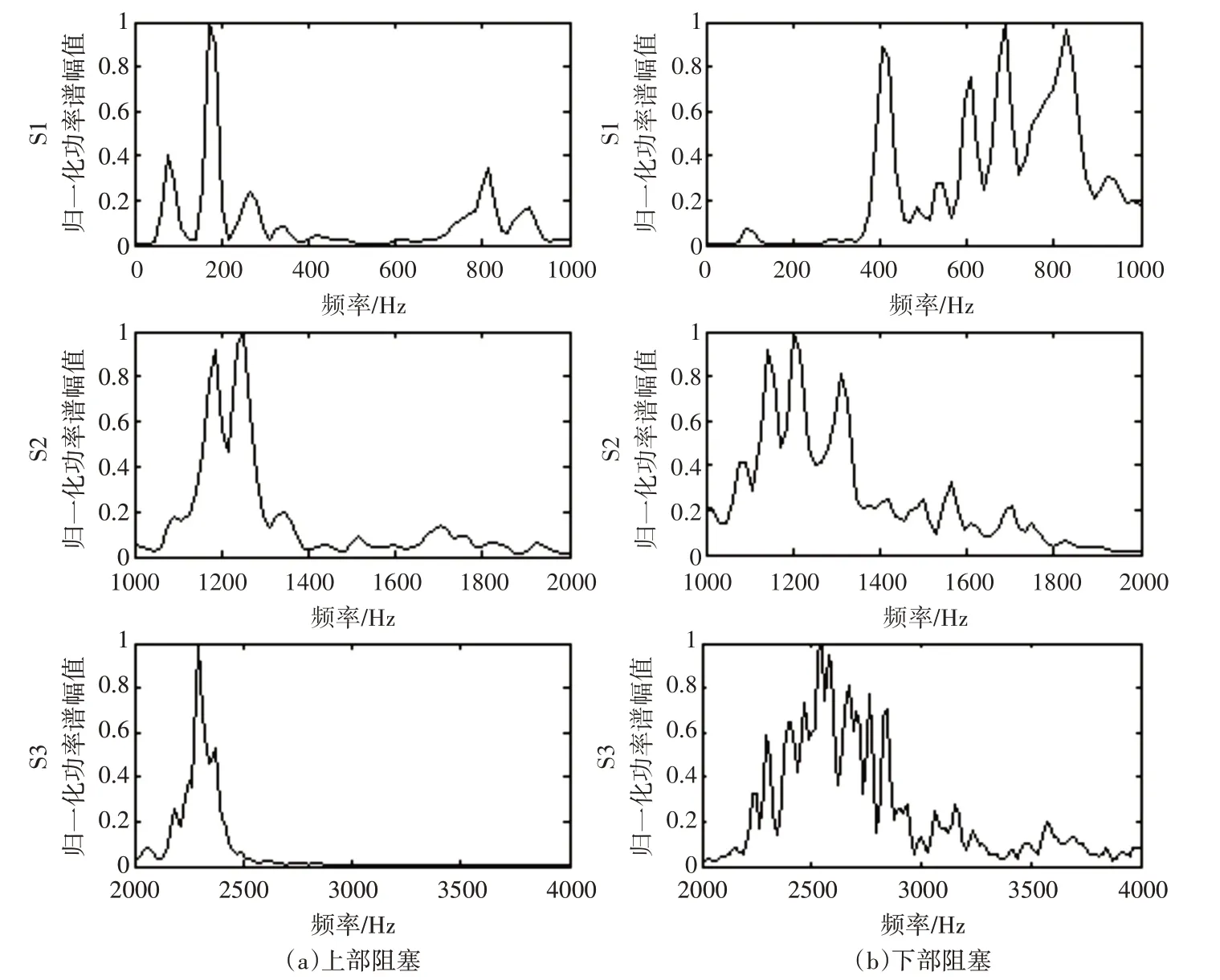
圖5 不同阻塞位置子帶功率譜估計圖
150例OSAHS病人的鼾音信號采用本文方法,上部阻塞和下部阻塞子帶信號功率譜估計的平均方差如表2所示。

表2 不同阻塞位置子帶信號功率譜估計的平均方差
綜合圖5、表2 可以看出上部阻塞和下部阻塞鼾音信號功率譜估計在方差方面,0~1000Hz 子帶和1000Hz~2000Hz 子帶差別不明顯,2000Hz~4000Hz 子帶的方差差別顯著,下部阻塞信號譜估計方差遠大于上部阻塞的鼾音信號,可以作為判斷阻塞位置的特征值。
6 結語
提出了基于小波分解的鼾音譜估計方法,將鼾音信號進行小波分解,再對提取的三個子帶信號分別采用Welch 法、多窗譜法、自相關法、Burg 法進行功率譜估計。研究表明,基于小波分解Welch 法適合于鼾音領域。利用本文方法分析150 例OSAHS阻塞位置,實驗發現上部阻塞信號在2000Hz~4000Hz 子帶的平均方差遠小于下部阻塞信號,可以將該特征信息作為判斷阻塞位置的標準,提供了一種簡單方便的檢測方法。

