一類邊替換圖的平均拉普拉斯多項式

闕林鳳，陳海燕

(集美大學理學院，福建 廈門 361021)

設G=(V(G),E(G))是n個頂點，m條邊的一個簡單圖，σ:E(G)→{+1,-1}是定義在G的邊集E(G) 上的映射，Gσ=(G,σ)稱為符號圖，G稱為它的基礎圖，σ是它的符號函數.對給定的一個符號圖Gσ，它的鄰接矩陣A(Gσ)=(aij)n×n定義如下：

符號圖Gσ的拉普拉斯矩陣L(Gσ)=D(G)-A(Gσ);這里D(G)=[d(v1),…，d(vn)]是G的頂點度對角矩陣.

圖G的一個邊子集M?E(G)稱為圖G的一個匹配，如果G中任意一個頂點最多關聯M中的一條邊.令M表示圖G的所有匹配的集合，則圖G的匹配多項式定義為[1]:

早在1978年，Godsil等[2]就證明了如下優美關系式：

這里∑(G)表示E(G)上所有符號函數的集合.關于匹配多項式的更多結果可參見文獻[3-4].受上面關系式的啟發，2020年，Zhang等[5]定義了一個新的圖多項式——平均拉普拉斯多項式：

2020年，Mohammadian[6]定義了直接類比匹配多項式——圖的拉普拉斯匹配多項式：

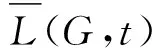
設G和T是兩個簡單圖，i和j是T中兩個固定頂點，滿足T-i和T-j同構，這里T-i表示由圖T去掉頂點i及其所關聯的邊所得到的圖.由G和T按下面的方法構造一個新的圖，稱為邊替換圖，記為G[T]:把G的每條邊e=(u,v)替換成T,使得i=u,j=v.

由G[T]定義，當T=P3是3個頂點的路，i和j是P3的兩個端點時，G[P3]就是G的剖分圖，記為S(G),即在G的每條邊插入一個新的頂點所得到的圖；當T=C3是3個頂點的圈，i和j是它的任意兩個頂點時，G[C3]就是G的三角擴展圖R(G),這兩類變換圖的各種性質得到了廣泛的研究[7-9].

設G是一個正則圖，本文將首先研究邊替換圖G[T] 和圖G的平均拉普拉斯多項式之間的一般關系式.然后在此基礎上，研究圖G的剖分圖、三角擴展圖的平均拉普拉斯多項式和圖G的平均拉普拉斯多項式之間的關系式，從而得到更具體的結果.

1 邊替換圖G[T]的平均拉普拉斯多項式

這部分將討論一般邊替換圖G[T]的平均拉普拉斯多項式，首先引進一些記號并給出幾個引理.

設G是n個頂點的簡單圖，令m(G,k)表示G的k邊匹配的個數，G的匹配生成函數

由匹配多項式的定義，很顯然

且有如下關系：

M(G,t)=tng(G,-t-2)；

(1)

引理1[5]設G是n個頂點，m條邊的簡單圖，S(G) 是G的剖分圖，則

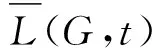
引理2[5]設G是n個頂點、m條邊的d-正則圖，則

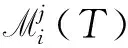
AT(t)=g(T-i-j,t),

注意到，當T-i和T-j同構時，CT(t)=DT(t).最近，Xin等[10]利用邊生成函數得到了邊替換圖G[T]和G的匹配生成函數之間如下的關系式.

引理3[10]設G是n個頂點、m條邊的d-正則圖，T是簡單圖，i和j是T中兩個固定頂點(i≠j),且T-i和T-j同構，則G[T]的匹配生成函數

現在給出關于邊替換圖G[T]的平均拉普拉斯多項式的結果.

定理1設G是n個頂點、m條邊的d-正則圖，T是n1個頂點、m1條邊的簡單圖，i和j是T中兩個固定頂點(i≠j),且T-i和T-j同構，則G[T]的平均拉普拉斯多項式

這里S(T)是T的剖分圖，

證明首先由邊替換圖G[T]的定義和剖分圖的定義，可得G[T]有n+(n1-2)m個頂點、mm1條邊；S(G[T])=G[S(T)]有n+(n1+m1-2)m個頂點.因此由引理1和式(1)得

tn+(n1-m1-2)mM(G[S(T)],t)=

tn+(n1-m1-2)mtn+(n1+m1-2)mg(G[S(T)],-t-2)=

t2(n+(n1-2)m)g(G[S(T)],-t-2)，

即

(2)

再由引理2、引理3和式(1)得

把上面的結果和式(2)結合在一起，就得到

結論得證.

下一部分將把上面的結果應用到剖分圖S(G)和三角擴展圖R(G)中，從而得到更具體的結果.

2 剖分圖和三角擴展圖的平均拉普拉斯多項式

設G是一個簡單圖，S(G)和R(G)分別表示它的剖分圖和三角擴展圖，這一部分討論剖分圖S(G)和三角擴展圖R(G)的平均拉普拉斯多項式.

定理2設G是n個頂點、m條邊的d-正則圖，S(G)是它的剖分圖，則

證明由定義，S(G)=G[P3],i和j是P3的兩個端點，因此很容易得到

AS(P3)(t)=AP5(t)=1+2t,

BS(P3)(t)=BP5(t)=t2,

CS(P3)(t)=CP5(t)=t+t2.

故

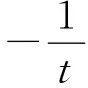
(2+d)t+2d).

結論得證.

在文獻[5-6]中已證明任意圖的平均拉普拉斯多項式的根都是非負實數，因此由定理2可以得到下面的推論.

和一個m-n重根2.

定理3設G是n個頂點、m條邊的d-正則圖，R(G)是它的三角擴展圖，則

證明由定義，R(G)=G[C3],S(C3)=C6.注意到i和j是C3的任意兩點，對應C6中距離為2的兩個頂點.因此經過計算得

AS(C3)(t)=AC6(t)=1+2t,

BS(C3)(t)=BC6(t)=3t2+2t3，

CS(C3)(t)=CC6(t)=2t+3t2，

進一步可得

故

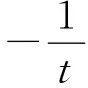
結論得證.