時域穩定的基礎頻響連續有理近似參數識別方法

唐貞云，王志宇，杜修力

(1. 北京工業大學城市與工程安全減災教育部重點試驗室，北京 100124；2. 中國地震局工程力學研究所，中國地震局地震工程與工程振動重點實驗室，黑龍江，哈爾濱 150080)

在土結動力相互作用問題的研究中，基礎部分通常采用頻響函數進行描述，其在連續時間情況下可以被近似為有理近似函數，該函數的穩定性與精度決定了基礎時域模型的穩定性與精度，進而影響土結相互作用系統動力時程分析。目前已有大量關于基礎頻響函數的研究，如：楊冬英等[1 ? 6]對多種不同土體條件中的樁基礎計算了其動力剛度；Valeti等[7 ? 11]分別針對筏板基礎、嵌入式基礎、條形基礎和樁筏基礎提出了基礎動力剛度數值計算方法；陳少林等[12 ? 15]研究了不同土體條件和基礎物理參數對基礎動力剛度的影響。為便于時域動力分析，在上述頻響函數基礎上，基于連續時間有理近似函數建立了大量時域集中參數模型，如：Wolf模型[16]、Wu-Lee模型[17]、Du-Zhao模型[18]、Wang-Liu模型[19]等。如何基于連續時間有理近似函數建立精確、穩定的基礎時域動力模型是實現土結動力相互作用時域分析的關鍵。大量學者基于有理近似函數開發了頻響函數時域動力模型參數辨識方法，如：Wolf等[16 ? 17,19 ? 23]分別采用有理近似函數擬合了基礎頻響函數，并將其展開為部分分式的形式，建立了不同的一階與二階彈簧—阻尼模型，給出了確保辨識模型穩定的后驗方法，但難以保證辨識效率；Wu等[24 ? 26]分別采用多項式消除法將有理近似函數展開為連分式，建立了嵌套的集中參數模型，但未對模型穩定性進行評價導致了部分模型在時程計算時發散；Okada等[27]采用最小二乘法擬合了基礎頻響函數，并建立了時域微分方程求解基礎響應，但其參數取值范圍為整個實數域且未對模型穩定性進行判斷或約束；王丕光等[28 ? 29]采用有理近似函數對水體剛度頻響函數進行了有約束的擬合，保證了函數的穩定性；Han等[30 ? 31]實現了剛性基礎及地下管道動力剛度矩陣的有理近似，但未給出有效的穩定參數識別方法。以上研究表明，滿足精度要求的頻響函數的有理近似模型不一定具有穩定性，大多數識別方法均未關注穩定性問題從而可能導致時程計算發散。為了保證辨識模型的穩定性，杜修力等[32 ? 33]利用罰函數給失穩參數組合增加懲罰值，保證了識別結果的穩定性，成為最常用的識別方法。

關于連續時間有理近似函數的參數識別研究，多數的研究中未考慮模型穩定性，少數學者采用后驗方法保證穩定性，但該方法得到有效結果的效率過低，在研究中難以應用。而罰函數法雖然可以得到穩定的結果，但在擬合過程中并不能保證每一組參數組合均可穩定，因此造成了計算效率不高，對多自由度系統適用性不強。本文基于線性控制理論將連續有理近似函數分解為一系列一階和二階子系統的組合，并從系統控制理論角度給出了有理近似函數穩定的理論約束條件，保證了辨識函數的絕對穩定性，基于此建立了一種新的連續時間有理函數參數識別方法。

1 基礎頻響函數的連續時間有理近似

土結動力相互作用研究中，常采用頻響函數對基礎進行描述：

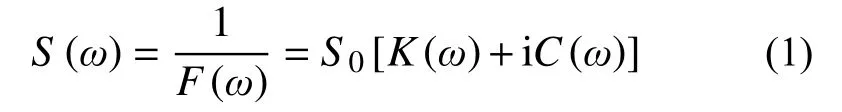
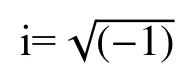
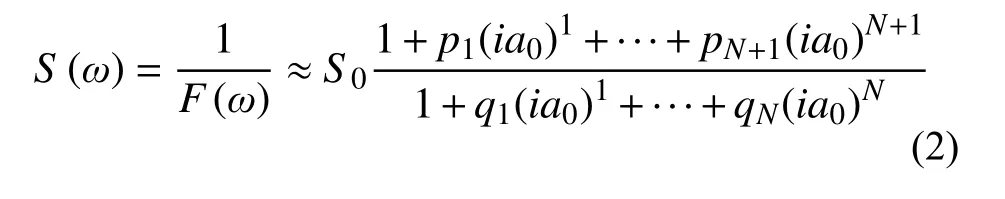
式中：pj和qj分別為分母多項式和分子多項式的待定系數，且均為實數；a0=ωd/Vs為無量綱頻率，其大小與地基長度d和土體剪切波速Vs相關；N為有理函數的階數。采用式(2)的系數可建立對應的集中參數模型，包括常見的Wu-Lee模型[17]、Du-Zhao模型[18]，如圖1、圖2所示。雖然采用連續時間有理近似函數可以較好地擬合基礎頻響函數S(ω)，但由于部分滿足精度的有理函數不具有時域穩定性，將其用于土結動力相互作用系統時域分析時會使動力時程計算發散。根據線性系統的穩定性理論[34]，連續時間有理近似函數的穩定性根據輸入與輸出的不同，可由其極點或是零點確定，如圖3所示：當輸入為位移，輸出為力，即擬合動力剛度函數時，當且僅當其極點全部位于S平面的左半平面，也即全部極點的實部均為負數時，函數穩定；而當輸入為力，輸出為位移，即擬合動力柔度函數時，當且僅當其零點全部位于S平面的左半平面可使函數穩定。假設式(2)的極點或零點采用sj表示，則其穩定條件可表示為：

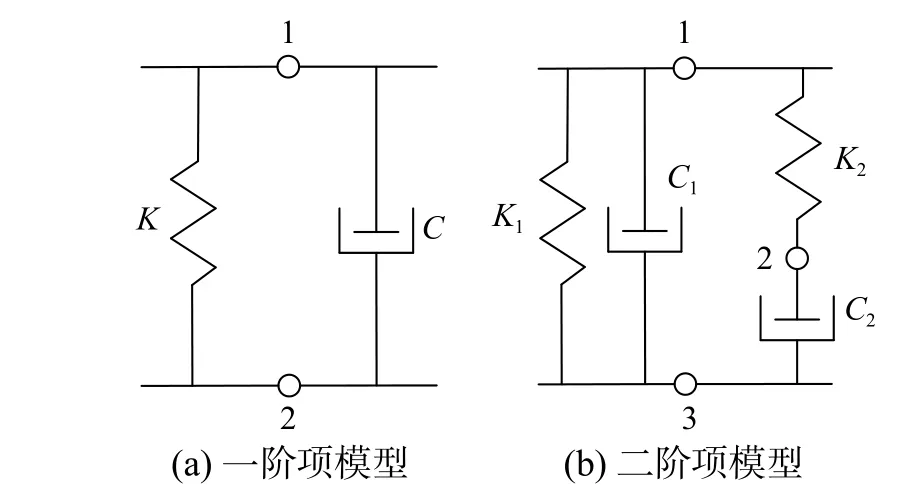
圖1 Wu-Lee模型Fig.1 Wu-Lee model

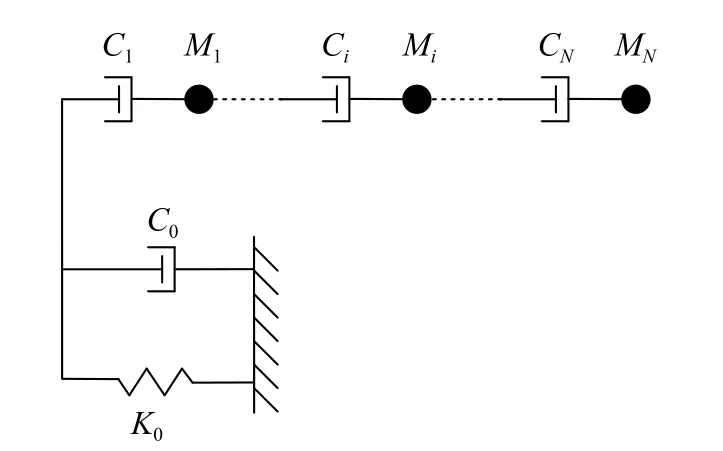
圖2 Du-Zhao模型Fig.2 Du-Zhao model

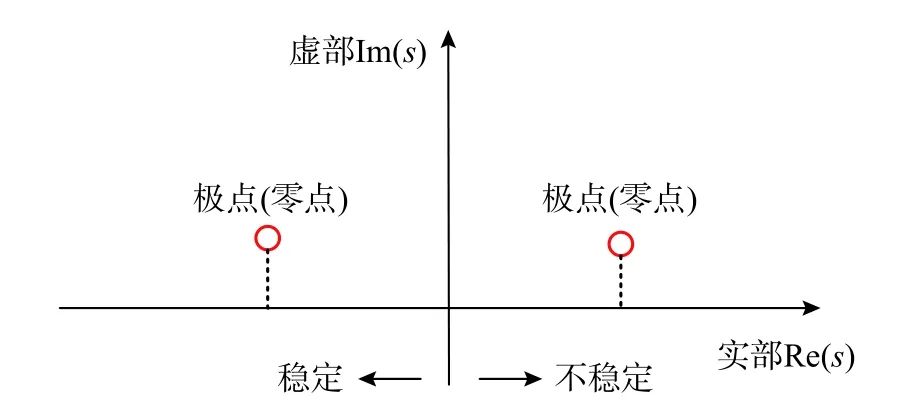
圖3 S平面穩定區域Fig.3 Stable area in S plane

以文獻[17]和文獻[32]中的圓形基礎搖擺頻響函數為例，其模型如圖4所示，基礎受到力矩(M)并產生轉角(θ)，圖中物理量分別表示：基礎的直徑d，土體的質量密度ρ，剪切模量G，泊松比ν=0.5。兩文獻的辨識結果如圖5所示，圖5(a)、圖5(b)分別為復剛度的實部與虛部，圖5(c)、圖5(d)分別為以兩者擬合參數計算的無量綱位移，由于文獻[17]未對函數的穩定性進行判斷，而文獻[32]采用罰函數對輸出結果進行了約束，因此對于同一頻響函數，前者進行時程計算是發散的，而后者是收斂的。

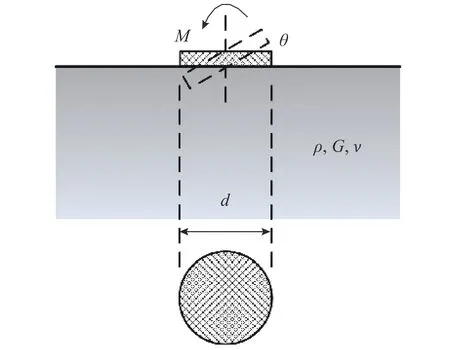
圖4 圓形基礎的搖擺運動Fig.4 Rocking motion of circular foundation

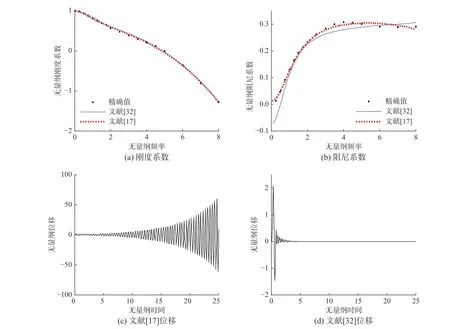
圖5 圓形基礎動力響應Fig.5 Dynamic response of circular foundation

由上述案例可知，對于連續時間有理近似函數，保證其在頻域內的擬合精度并不能達到實際應用的要求，還需要保證有理近似函數穩定性以用于時程分析。

2 穩定參數識別方法

為了確保基于連續有理近似的基礎時域動力模型在時程分析中的有效性，需要在時域參數辨識過程中確保模型對基礎阻抗描述的精確性和模型的時域穩定性。前述可知，既有參數識別方法要么只考慮精度不考慮穩定性，要么通過后驗法判斷模型穩定性，即先滿足頻域響應精度，而后進行穩定性判別，當發現不穩定時重新識別參數，直到獲得同時滿足精度和穩定性條件的參數后停止識別。如果預先確定滿足穩定性的參數條件，然后在該范圍內尋找滿足精度要求的最優參數將會更有效。

2.1 穩定參數約束條件

根據系統穩定性理論[34]，連續有理近似函數穩定的充分必要條件為全部極點的實部小于0，因此若是可以通過約束其參數的方法規避失穩值，即可保證擬合過程的穩定。由式(2)可知，需要先得到有理近似函數的參數才能獲得其極點，這就是現有方法無法提前確定穩定參數范圍的原因所在。根據線性控制系統[34]，每個多階系統均由一些列一階和二階子系統組合而成。基于該概念，將式(2)的分母多項式通過部分分式展開分解為l個二階項與N?2l個一階項的乘積，而分子多項式不變，如式(4)所示：

溫度升高會影響雞的休息行為、生理行為，最終導致生產性能下降。但目前關于偏熱刺激對肉雞休息行為、生理行為和生產性能的影響研究相對較少，因此本次研究對上述幾項指標進行了研究現狀，具體研究內容介紹如下。

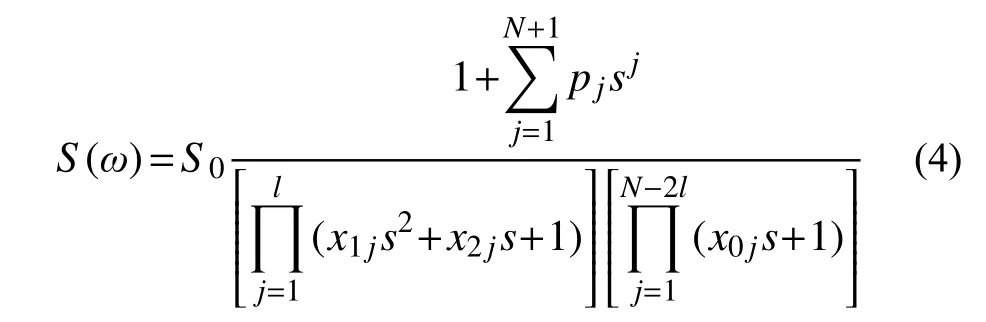
式中：s=ia0；xkj為部分分式展開后的分母多項式系數，k=0,1,2；N為原函數的階數；l為二階系統的個數。由于二階系統可以看作兩個一階系統，因此可以認為：當N為偶數時，N=2l，即式(4)中沒有一階項；當N為奇數時，令N?1=2l，即式(4)中僅存在一個一階項。因此，根據求根公式可以得到式(4)的極點為：

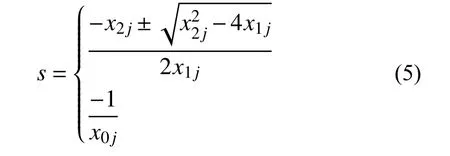
式中：第一個根為二階項的共軛根；第二個根為一階項的根。一階項根的取值范圍可以簡單地得到：

而由于共軛根為實數或是復數時，所需進行穩定性判斷的參數不同，因此將共軛根分為實數根與復數根兩部分討論：

1)共軛根為復數

由于共軛根為復數，根據穩定性條件：極點實部小于0。可以得到：

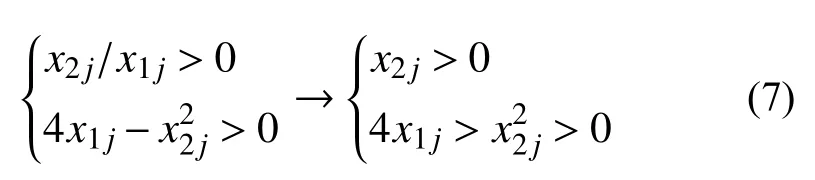
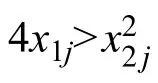
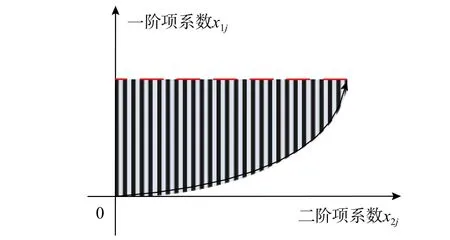
圖6 復數根時穩定參數界限Fig.6 Stability parameter boundary for complex roots

2)共軛根為實數

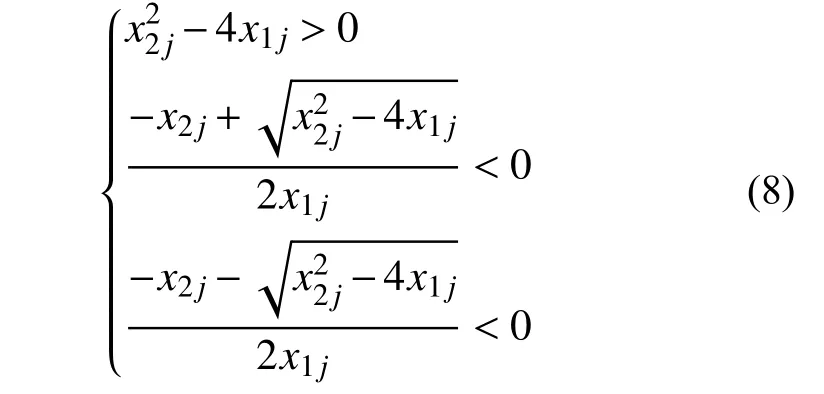
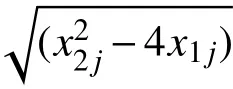
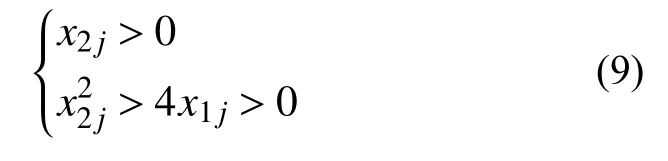
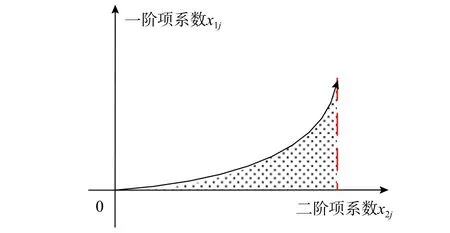
圖7 實數根時穩定參數界限Fig.7 Stability parameter boundary for real roots

3)穩定參數界限

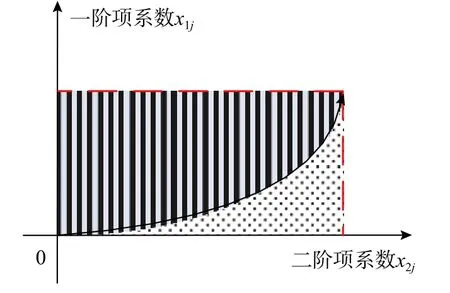
圖8 穩定參數界限Fig.8 Boundary of stable parameters

2.2 參數識別方法

得到了新的有理近似函數形式及其穩定參數取值范圍后，如何取得最優的擬合結果是一個函數尋優問題。優化算法可以分為全局優化算法和局部優化算法，常見的全局優化算法有進化算法、遺傳算法、粒子群優化算法等等，而常見的局部算法有單純形法、序列二次規劃算法等等。本文以Wang等[35]將遺傳算法與單純形法結合形成的混合算法為基礎，采用序列二次規劃算法(SQP算法)代替單純形法，形成遺傳-SQP算法用于求解連續時間有理近似函數的待定系數。遺傳算法作為全局優化算法，不需要給出合理的初始值，可以從多個任意初始值開始尋優，搜索范圍大，利于全局擇優。而SQP算法作為局部優化算法可以從遺傳算法得到的全局最優解中選擇初始值，避免了因初值選擇不當導致的擬合效果差。此外，采用SQP算法代替單純形法可以將無約束優化問題變為有約束優化問題，即將式(10)所示參數約束條件加入尋優算法中，計算流程圖如圖9所示。

3 數值算例驗證

為了驗證本文方法的有效性，本節分別采用簡單與復雜的基礎頻響函數進行對比研究。具體參數辨識流程如圖9所示，首先根據頻響函數曲線獲得函數的實部與虛部，然后根據第二節穩定范圍編寫程序，通過遺傳算法與SQP算法迭代識別，在滿足精度要求后將結果輸出。本文進行參數識別時采用式(4)給出的新形式有理函數進行辨識，辨識的目標函數為：

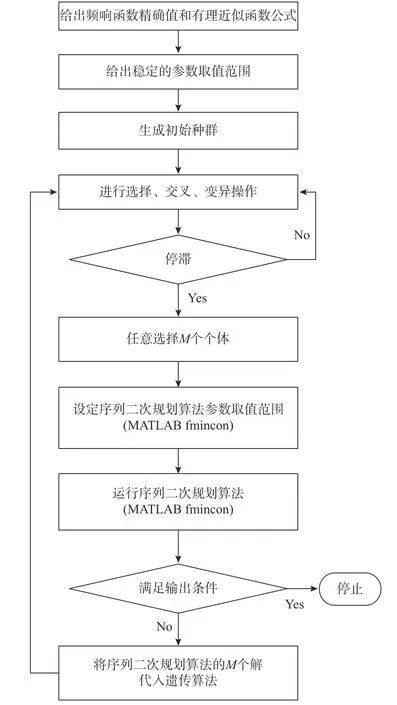
圖9 參數識別流程Fig.9 Parameter identification process

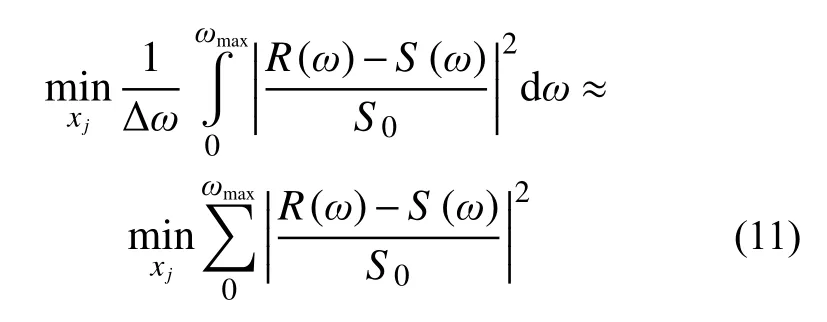
式中：xj為待識別參數；ω為外荷載頻率；R(ω)為連續時間有理近似函數；S(ω)為動力剛度頻響函數。

而為了對辨識結果的精度進行定量評估，取精確解與識別函數之差絕對值積分面積占精確解絕對值積分面積的比值作為誤差評價指標，其中實部與虛部各占50%，如下式所示：

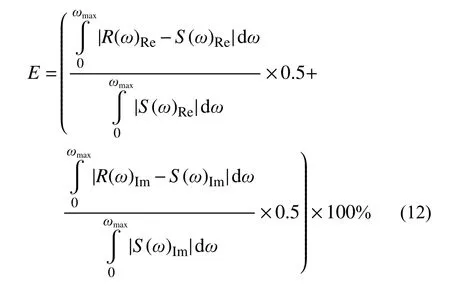
式中：E表示識別模型誤差；R(ω)Re、S(ω)Re、R(ω)Im和S(ω)Im分別表示有理函數與動力剛度精確值的實部與虛部。

算例1. 圓形基礎搖擺頻響函數

對于簡單的頻響函數，本文以圖4、圖5所示的圓形基礎搖擺運動及無約束擬合失穩案例為例，其基礎頻響函數具體數值取自文獻[32]。參數辨識分別采用罰函數法[32]和本文方法進行對比，有理函數階數取為N=3/4/5/6/7階，辨識結果如表1、表2和圖10所示，其中，表1計算效率單位為秒。由圖10(a)、圖10(b)可以看到，兩種方法辨識結果均可較精確地描述動力剛度，采用式(12)計算所得誤差均小于1%。事實上，當采用N=3階有理函數時，辨識誤差約為6.5%，但當階數增加，擬合精度迅速增加，在N=4階及以上時，誤差均低于1%，證明兩種方法擁有很高的精度。由于靜剛度不影響穩定性，因此采用表2參數，將EL-Centro波作為地震動輸入，利用Du-Zhao模型[18]和Newmark-β法進行無量綱時程計算。由圖10(c)、圖10(d)可以看到，兩種方法均可保證時程計算的穩定性，且時程曲線完全一致。由表1可知，在計算效率方面上，本文方法略優于罰函數法。兩種方法分別采用3階～7階函數對頻響函數進行識別，擬合用時均隨階數增加而增加。但罰函數法擬合用時隨階數增加是成倍增長的，而本文方法效率損失隨階數增加較低，用時從罰函數法的約100%逐漸降低到約65%。原因在于本文方法取值區間內可保證函數穩定，而罰函數法需要求解高階多項式判斷穩定性，且階數越高效率損失越大。

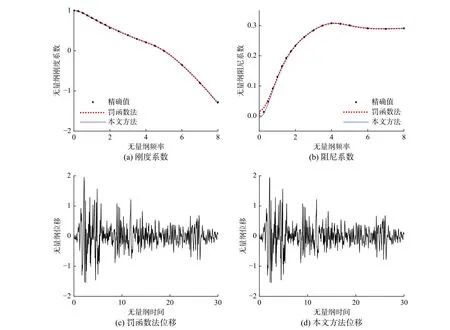
圖10 圓形基礎搖擺頻響 5階有理函數辨識結果Fig.10 Identification results of a 5th-order rational function for rocking frequency response of a circular foundation

表1 圓形基礎搖擺頻響函數辨識效率Table 1 Identification efficiency of rocking frequency response of a circular foundation

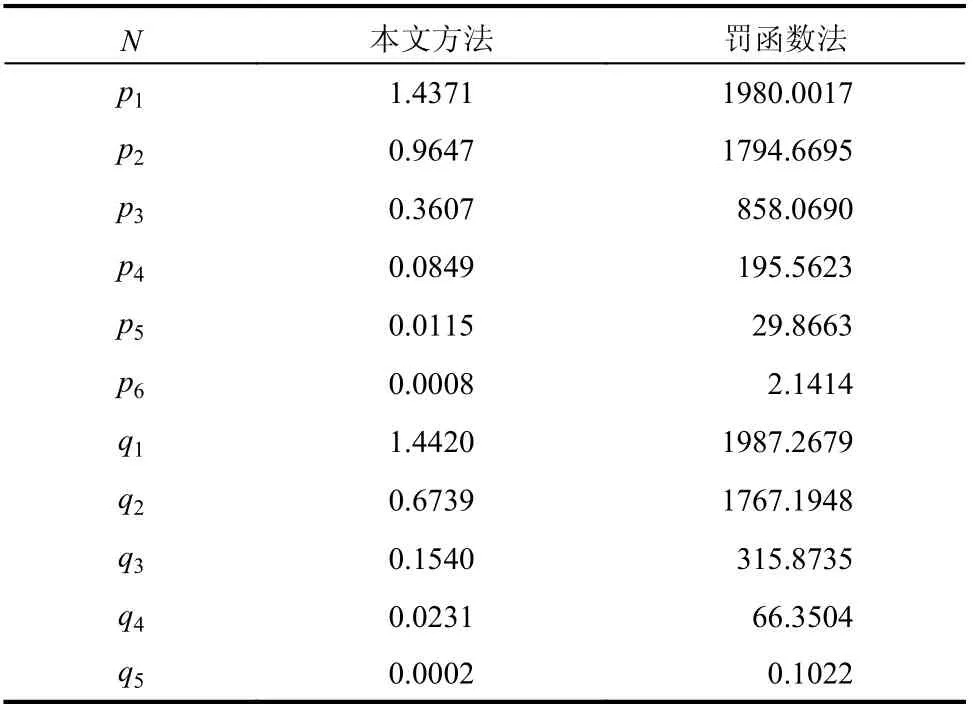
表2 5階有理函數參數Table 2 Parameters of 5th-order rational function

算例2. 圓形基礎水平頻響函數

為驗證函數階次對于辨識精度的影響，分別采用不同階次的有理函數對圖11所示的圓形基礎水平運動復雜頻響函數進行參數識別，其值由文獻[36]的圖7得到。圖中PeiωΔt和ueiωΔt分別為基礎受到的

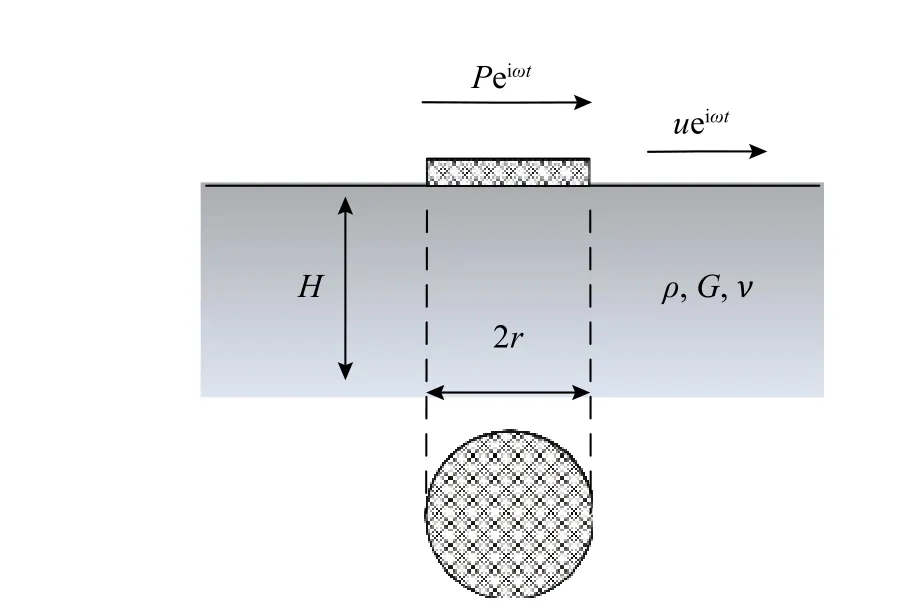
圖11 圓形基礎的水平運動Fig.11 Horizontal motion of circular foundation

水平外荷載與產生的位移。基礎參數為：基礎半徑r=10 m，剪切波速Vs=100 m/s，土體泊松比ν=1/3，土體阻尼比ξ=0.05，土層厚度H=2r。由于其基礎動力剛度隨頻率變化劇烈，因此利用連續時間有理近似函數擬合具有挑戰性[32]。本文分別采用算例1中的兩種方法，取階數N=3/5/7/9/11階進行擬合。函數的擬合精度采用式(12)進行評價，辨識結果如圖12、圖13所示，辨識效率與誤差和曲線參數如表3、表4所示。

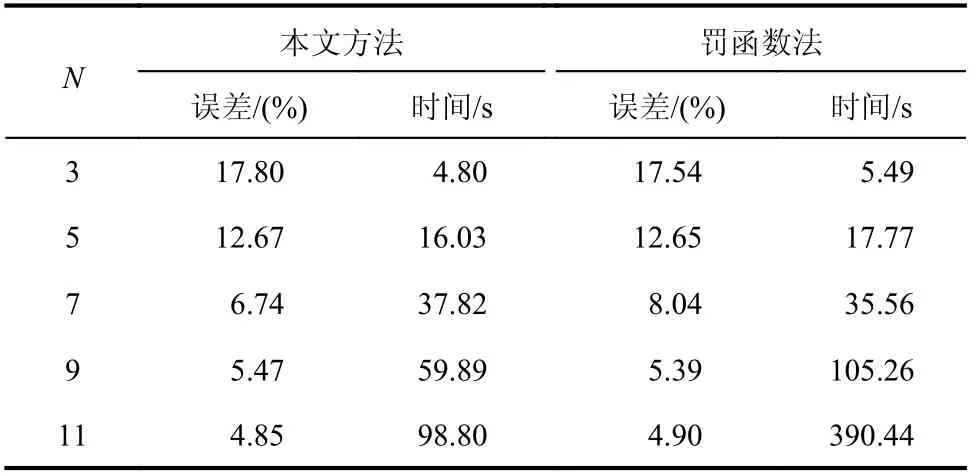
表3 圓形基礎水平頻響函數辨識精度及效率Table 3 Identification accuracy and efficiency of horizontal frequency response for a circular foundation

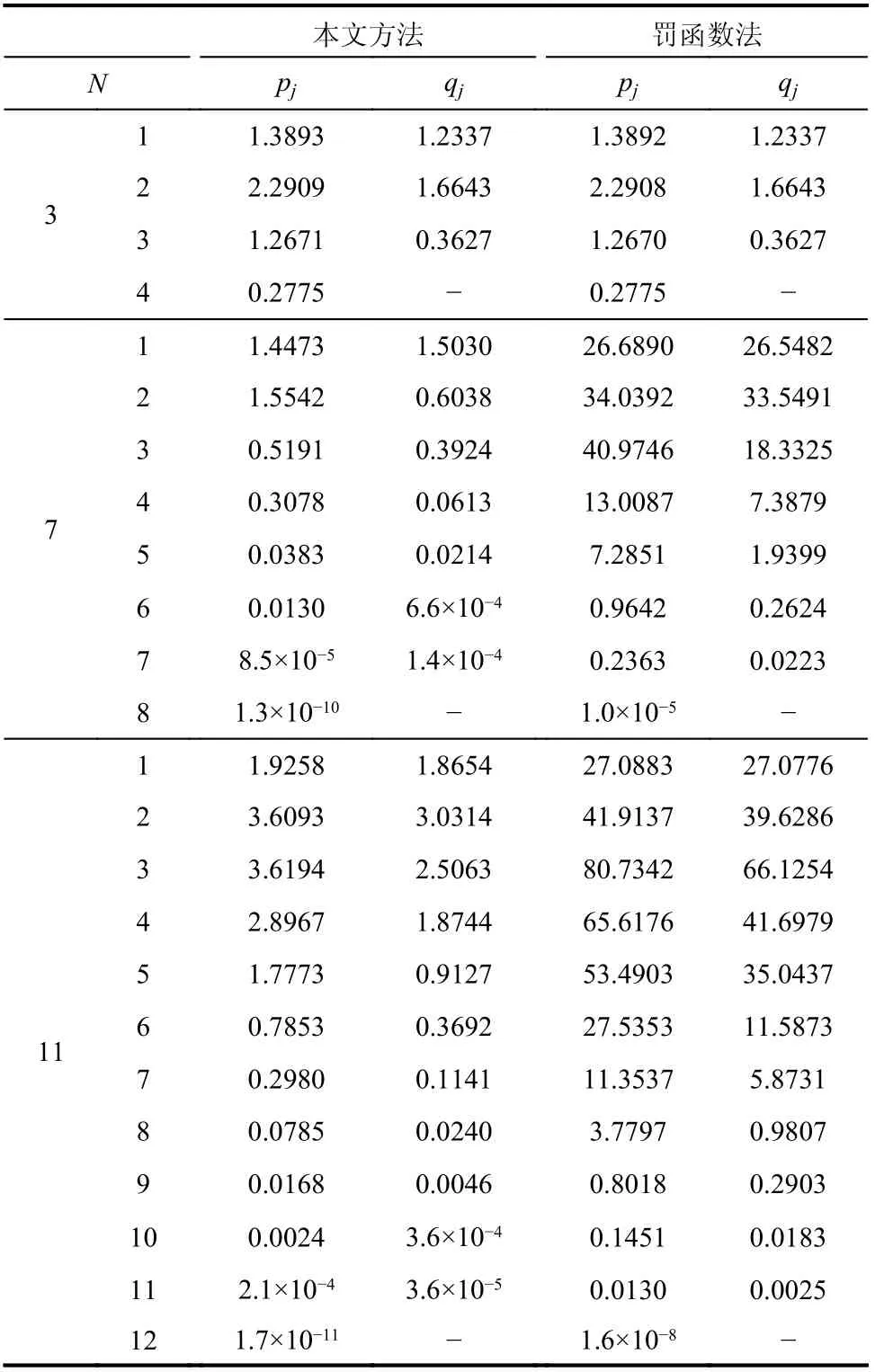
表4 不同階次有理函數參數Table 4 Parameters of rational functions of different orders

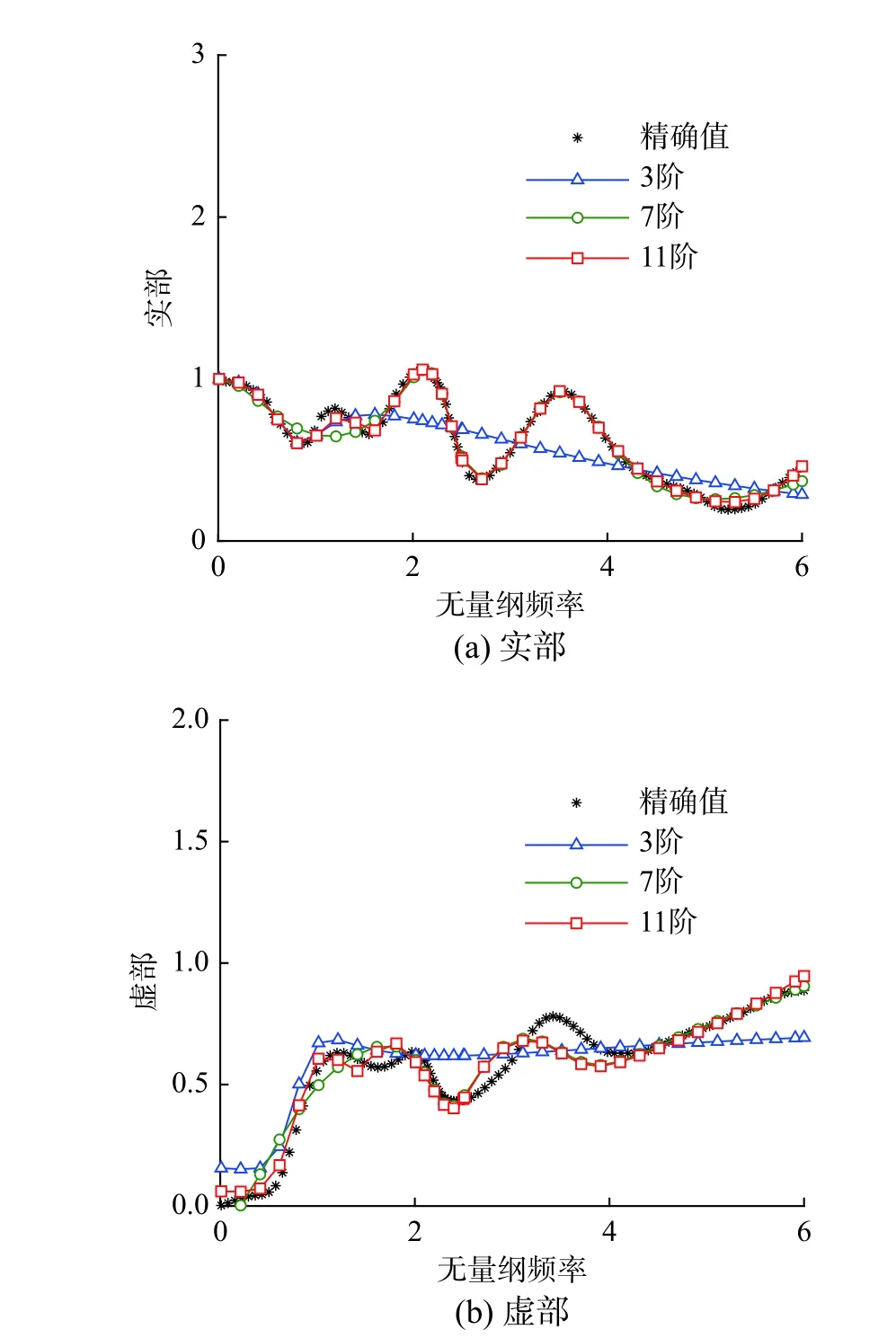
圖12 本文方法不同階次有理函數辨識結果Fig.12 Identification results of proposed method for rational functions of different orders

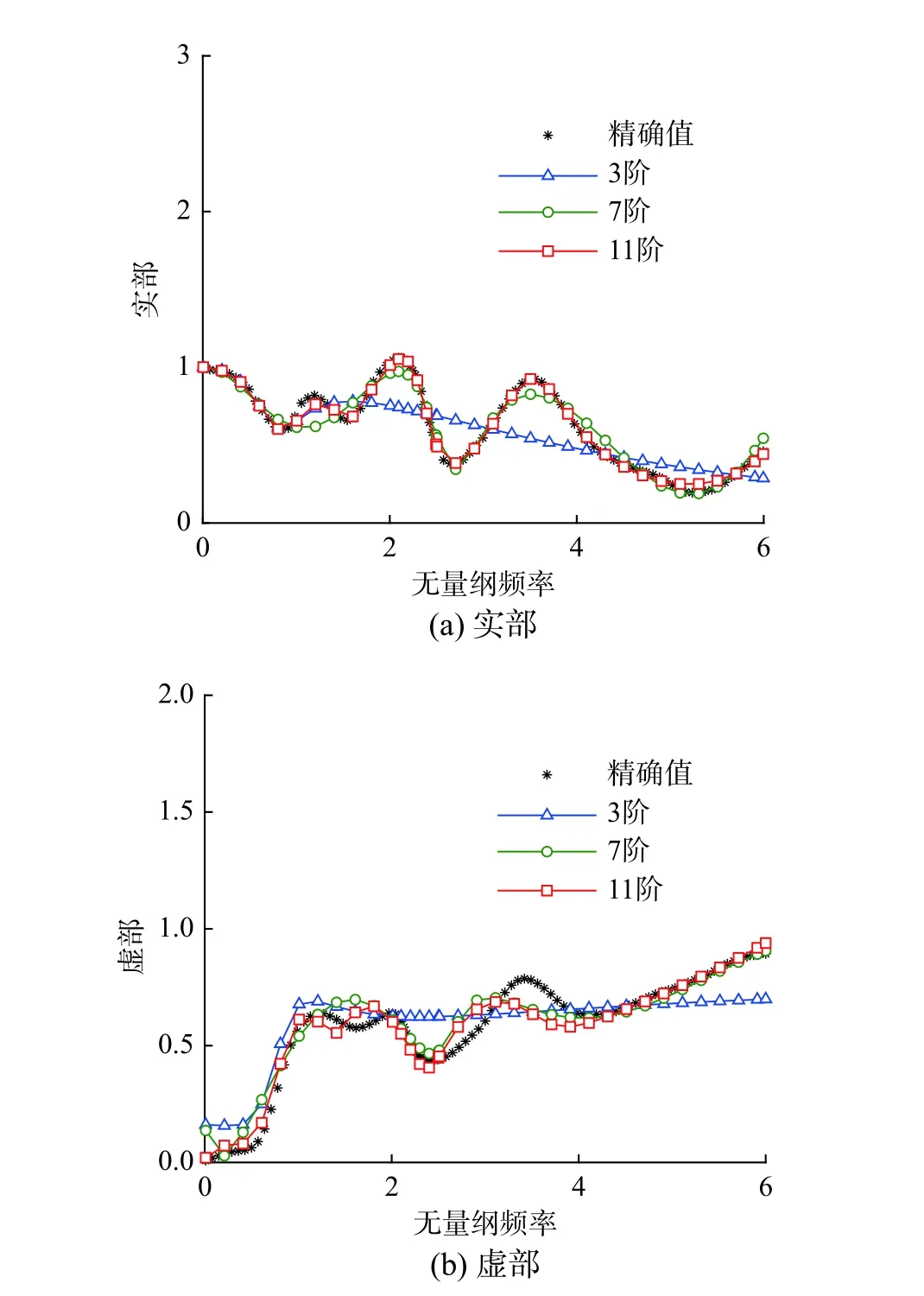
圖13 罰函數法不同階次有理函數辨識結果Fig.13 Identification results of penalty function method for rational functions of different orders

由表3、圖12和圖13可以看到，采用不同階次的有理函數辨識時，兩種辨識方法精度基本相同，辨識精度隨階數增加逐漸提高，當采用3階函數擬合時，效果較差，整體誤差均約有18%，難以擬合復雜函數。但階數增加到7階時，整體誤差降低到約7%，此時采用有理函數已可以較好的擬合頻響函數，而再增加階數，擬合精度進一步提高，但此時提升較小，達到11階時，整體誤差約為5%。但從辨識效率來看，當階數較低時，兩種方法擬合用時均較短，而隨階數增加，罰函數法擬合用時迅速增加。當階數達到11階時，本文擬合用時僅為98.8 s，而罰函數法則用時390.44 s，遠大于本文方法。證明了本文方法在同時保證擬合精度與效率上的優勢。

4 結論

針對基礎頻響連續時間有理近似函數的參數識別難以同時保證穩定性、精度及計算效率的問題，本文提出了時域絕對穩定的連續有理近似函數參數識別方法。采用不同基礎頻響函數，對本文方法和罰函數擬合方法就穩定性、精度及計算效率等方面進行了對比分析，驗證了本文方法的有效性與優勢。得到主要結論如下：

(1) 從線性系統理論角度將基礎頻響函數連續有理近似分解為一階與二階系統的組合，并根據其根的穩定性條件建立了被辨識參數的穩定界限。據此，采用遺傳-序列二次規劃算法建立了時域穩定的參數識別方法，保證了識別函數時域模型的絕對穩定性。

(2) 單自由度基礎頻響函數對比仿真表明：對于簡單函數模型本文方法與既有方法擁有同等精度，但在計算效率上明顯優于既有方法，本文方法用時在不同階次均少于既有方法，最大可節約耗時35%左右；對于復雜函數，通過增加有理近似函數階次可保證模型精度，采用本文方法時也可保證一定的效率，在達到11階時用時小于100 s，而既有方法需要390 s。這不但同時確保了頻響函數識別的穩定性、精度和效率，更提高了多自由度頻響函數識別的適用性。