時空軌跡相似性度量方法探討

郭博雷 田晗 湯玲 杜志強

（1.中國電子科技集團公司第二十七研究所 河南鄭州 450047；2.南京北斗創新應用科技研究院有限公司 江蘇南京 211500；3.武漢大學測繪遙感信息工程國家重點實驗室 湖北武漢 430072）

作為一個整體概念，時空不僅是現實物體存在的維度，也是人類認知和認識世界的模式［1］。具有時間和空間屬性的數據或信息出現在日常生產、生活和經濟文化活動的各個領域。時空軌跡，即記錄運動物體位置隨時間變化的數據，是最典型的時空數據類型。近年來，隨著各種傳感器和定位芯片的大量安裝，數據不斷積累，數據內容不斷豐富，它所包含的信息和知識反映了運動物體的不同運動規律和行為模式，具有相當大的挖掘價值。其中，軌跡相似性是軌跡之間最基本的模式。如何綜合考慮軌跡形狀和位置不確定性等因素，衡量軌跡和軌跡子段之間的相似性，是許多軌跡數據挖掘和分析應用的要解決的問題。

軌跡相似性分析和相似模式計算是時空數據挖掘的重要內容，是時空數據諸多應用的基礎，如異常的軌跡聚類、熱點和頻繁模式挖掘等相關領域一直保持著較高的研究興趣［2］。時空建模、時空分析、時空模式挖掘等相關領域的研究一直占據著相當大的比重，尤其是基于軌跡數據分析、挖掘和計算的研究，往往基于新的底層模型擴展新場景。空間數據新應用的新時空軌跡建模和相似性分析再次成為該領域學者關注的焦點。

時空軌跡相似性分析屬于計算機科學和地理信息科學的交叉領域，其關鍵技術包括通用時空數據模型、時空軌跡數據模型、軌跡相似性度量方法、軌跡子段匹配與相似模式挖掘等。結合本文研究內容，下面對時空數據模型、時空軌跡模型及軌跡相似性度量與計算等方面的研究現狀作分別介紹。

1 時空數據模型

時空動態變化過程是空間信息在時間域的擴展和完善，傳統的空間對象就是時空對象在某一時刻的空間瞬態［3］。時空數據著重于時空過程中的時序關系和時空因果聯系，使設計者、開發者和用戶能夠更好地實現時空對象時間和空間信息的動態表達與建模。時空軌跡的表達與建模更加依賴于通用時空數據模型的設計。時空數據建模所面臨的主要難點如圖1所示［4］。

圖1 時空數據建模所面臨的主要難點

在此領域還有多位學者引入了多樣化的建模方法，提出了一系列各有側重的模型成果，如圖2所示［5］。

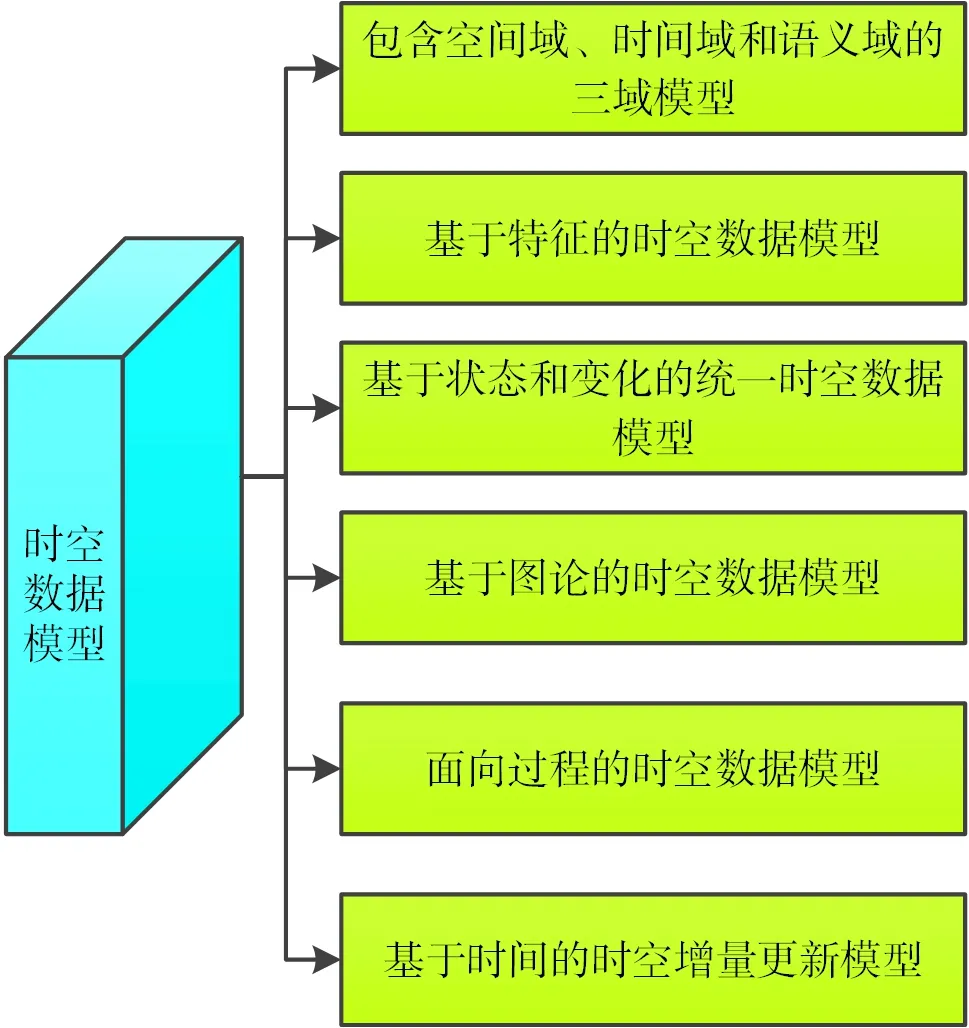
圖2 時空數據模型

但這些模型大多只是在上層設計概念模型，沒有觸及數據底層的組織方式，所以，大多是屬于數據與應用之間的中間層級模型，不具備通用性，且對時空因果、時空關聯等模式支撐不足，無法在更廣泛的問題場景中發揮作用。所以，業界也出現了一些從數據生產和轉換層面著手的模型設計，典型代表就是英國陸地測量部的MasterMap項目。如今，大多數GIS 都是基于圖層要素模型系統來組織和管理空間數據的。基于OGC 標準下的單元素模型，形成一套結合空間對象和平鋪地圖的混合數據結構。底層空間數據庫也主要基于關系模型。

2 軌跡數據模型

隨著各類位置傳感器在移動實體的廣泛安裝，移動對象的軌跡數據成為數據量最大的時空數據類型，最常見的為記錄車輛、船只、飛行器、野生動物等移動物體的軌跡數據。許多研究部門和企業都公開了大規模的軌跡數據集，以支撐更加開放、多元的科學研究，例如，滴滴公司的“蓋亞”計劃公開了數個城市的滴滴快車軌跡數據，數據量達到了數百GB。相應地，面向新的數據現狀和應用場景，針對軌跡數據建模的研究也層出不窮，取得了許多新的進展。軌跡模型的研究可以追溯到20世紀70年代，人們為了描述颶風的移動軌跡，反映颶風異動情況和態勢，以進行后續的分析和預測，設計了最初的軌跡數據模型［6］，后續也發展了很多軌跡數據模型，如圖3所示。

圖3 軌跡數據模型類別

在軌跡不確定性建模方面，一種多粒度模型值得特別注意，它使用棱錐狀結構來描述一個移動的物體在兩個位置采樣點之間可能的路徑區域，用首尾相接的Bead 形成的連續的珠串表示整條軌跡［7］。其中使用的Bead模型來源于時間地理框架，因形態特征也被稱為Prism模型，其數學基礎在多個文獻中得到了進一步的闡述，包括時空路徑和時空棱錐等時間地理學的基本要素。時空Bead 模型對軌跡數據離散采樣和插值所帶來的位置不確定性進行了建模，但時空三維空間中融合了空間和時間特征的立體Bead 不便于處理和計算。一個經典的簡化方法是將Bead 模型投影到空間二維平面上（見圖4），成為一個以采樣點為焦點的橢圓，再進行后續的分析和計算。很多文獻已經基于Bead投影橢圓進行了可達性計算、位置分布預測等研究工作［8］。

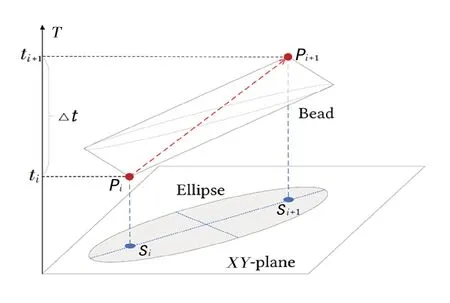
圖4 B ead 模型在空間平面上的橢圓投影

其他考慮空間位置不確定性的軌跡模型還包括緩沖區模型、圓筒模型、立方網格模型等，大多采用將采樣點或采樣點間的插值線向外按不同的幾何模型擴展一定的距離，作為移動對象可能的位置范圍［8］。

3 時空軌跡相似性度量方法分類

3.1 時空軌跡

軌跡數據庫T={T1，T2，T3，…，Tf}，包含一系列的原始軌跡，f表示軌跡庫中軌跡的條數，其中，每一條軌跡Tj(1≤j≤f) 都是由GPS 等設備記錄的位置點{p1，p2，p3，…，pn}的集合，pi表示的軌跡點通常使用經度、緯度、時間戳表示，即(pi·x，pi·y，pi·t)，i表示點在軌跡中的位置。查詢序列也是一條軌跡，本文用Q={q1，q2，q3，…，qm}表示，其中，m表示查詢序列中元素的個數。

3.2 時空軌跡相似性度量方法分類

由于時空軌跡相似性度量主要依賴于軌跡之間距離的定義，軌跡之間的距離使用軌跡之間的匹配程度來表示，不同的軌跡匹配度量方法對軌跡之間的匹配程度有著不同的解釋［9］。

本文將時空軌跡相似性度量方法分為兩類：基于軌跡點的相似性度量方法和基于軌跡段的相似性度量方法，如圖5所示。由于軌跡主要是以軌跡點的方式進行存儲，當對軌跡進行相似性度量時，最直觀的方式就是利用兩條軌跡中對應軌跡點之間的距離來度量軌跡之間的相似性［10］。基于軌跡點的相似度測量方法有很多種，每種方法都有自己獨特的相似度定義和應用場景。例如，一些測量方法認為兩條軌跡只需要部分相似，它們是相似的；有些測量方法認為兩條軌跡整體上是相似的，它們是相似的。因此，本文將基于軌跡點的相似度測量方法分為兩類：全局匹配度量法和局部匹配度量法，具體分類如圖5所示。

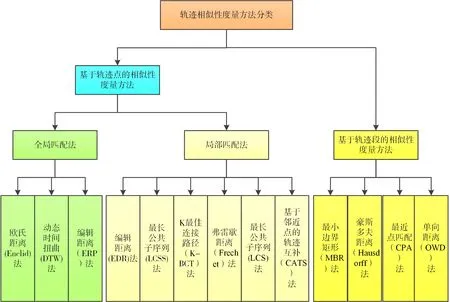
圖5 軌跡相似性度量方法分類

4 結語

時空軌跡的相似性分析與計算是眾多軌跡模式挖掘應用的重要手段，而軌跡的相似性度量是相似分析等上游應用的重要基礎。對不同數據條件和應用場景的軌跡相似性度量進行研究，具有重要的理論和實用價值，并可以有效促進空間數據分析與挖掘方法多樣化發展。