基于混沌理論的降水量預測方法研究

舒濤，路昊天，曹景軒，葉唐進，陶偉，付潤藝，李豪

基于混沌理論的降水量預測方法研究

舒濤1，路昊天2，曹景軒3，葉唐進4，陶偉3，付潤藝3，李豪5,6,7*

（1.中國海洋大學 海洋地球科學學院，山東 青島 266100；2.桂林理工大學 地球科學學院，廣西 桂林 541004；3.西藏大學 工學院，拉薩 850000；4.大連理工大學 建設工程學部，遼寧 大連 116024；5.中國科學院 山地災害與地表過程重點實驗室，成都 610041；6.中國科學院 水利部成都山地災害與環境研究所，成都 610041；7.中國科學院大學，北京 100049）

【】得到精確度較高的月降水量預測值。首先利用C-C關聯積分法來確定波密站月降水量非線性系統的時間延遲和嵌入維數，再對月降水量時間序列進行相空間重構，并利用小數據量法求取Lyapunov指數來判斷月降水量時間序列的混沌特征，然后構建Volterra模型分別進行短期5 a和長期15 a降水量預測，將其預測小波預測模型和SVR預測模型的預測值對比，最后對Volterra短期預測模型進行疊加預測誤差分析和模型推廣分析。Volterra模型對混沌特征明顯的月降水量進行短期預測時，其和分別為4.04%和0.941，相比小波和SVR模型來說具有較高的預測精度，同時疊加預測誤差較小，其為7.657%，為0.894；而在長期預測時，該模型預測精度不如SVR模型；同時Volterra模型對混沌特征弱的月降水量進行短期預測時，其模型預測效果并不理想，為54.855%，僅為0.566。該方法能提供精確度較高的降水量預測值，為降水量的預測提供一種新的方法。

混沌理論；相空間重構；Lyapunov指數；Volterra濾波器；降水量預測

0 引 言

【研究意義】在G318國道林芝至波密段地質災害頻發，導致地質災害頻發的主要誘發因素之一是降水[1]。若能較精確地預測該地區的降水量，則能對地質災害起到預警預報的作用。由于降水量是非線性、非穩定性的時間序列，在月降水系統中可能存在著混沌序列[2]；因此，能否將混沌理論應用于月降水量的預測來提高模型預測精度，成為水文預測中的研究熱點。

【研究進展】混沌是指具有確定性的動力學系統受到非線性變量的影響而產生的一種沒有規律的，但有貌似規律的現象[3-4]。在早期混沌研究中，Lorenz[5]研究長期氣象預測時發現了混沌現象“蝴蝶效應”，1987年，Hense[6]在研究月降水量時間序列關聯維數時同樣發現混沌現象，此后，許多學者在降水量時間序列中也發現了混沌現象[7-9]。隨著對混沌現象的研究逐漸深入，王文等[10]認為對水文系統中的混沌現象研究很有必要。Sivakumar等[11]在月徑流預測中運用混沌理論中的重構相空間法構建預測模型，發現其具有較高的預測精度，并且隨著一系列基于混沌理論的預測算法的出現，混沌理論在水文系統中應用越來越多；因此，國內外學者便嘗試將基于混沌理論的預測算法用來對徑流和降水量進行預測。但在混沌預測的早期研究中，主要是將混沌理論的重構相空間法應用于降水量預測[12-13]；在21世紀初，神經網絡算法得到了迅速發展，便有部分學者嘗試運用混沌理論與神經網絡相結合的方法來對降水量進行預測[14-18]，其發現混沌理論能夠提高這些神經網絡預測模型的精度。隨后，便有一批國內外的學者將混沌理論應用于神經網絡模型，以期提高模型預測精度[19-21]；但在近年的研究中，混沌理論常應用于遺傳算法與小波變換中，以期獲得更高的預測精度[22-25]。【切入點】一般來說降水量時間序列為離散時間序列，其預測思路一般是對離散時間序列進行分解，來分析其發展規律[26]。但是利用傳統的方法只能發現降水量時間序列中很少的信息，而混沌理論卻是從一個新的維度來揭露降水量時間序列的內部變化特征，即從相空間上分析其運動特征[27]。這么多年來，許多專家學者利用混沌理論對水文學的各個領域進行了初步的研究，并取得了豐碩的成果。但是至今為止，對降水量時間序列的混沌研究仍處于探索階段，仍還有許多問題有待研究。

【擬解決的關鍵問題】綜上所述，在降水量時間序列中確實可能存在混沌現象，但近年來國內外學者只是將混沌理論應用于傳統的降水量預測模型中，而沒有使用專門預測混沌特征的預測模型如Volterra模型等；也沒有進一步驗證這些模型是否對混沌特征弱的降水量時間序列仍具有較好的預測效果。首先對波密站1961—2018年月降水量進行特征分析，其次利用C-C關聯積分法來確定波密站月降水量系統中的時間延遲和嵌入維數，再對月降水量時間序列進行相空間重構，并利用小數據量法求取Lyapunov指數來判斷月降水量時間序列的混沌特征，然后構建Volterra模型分別進行短期5 a和長期15 a降水量預測，將其預測值與小波預測模型和SVR預測模型的預測值對比，最后對Volterra短期預測模型進行疊加預測誤差分析和模型推廣分析。

1 降水量特征分析

根據1961—2018年波密站的降水量數據（圖1）可知，2015年波密站年降水量達1 169 mm，為歷年降水量最高值；1964年年降水量439.9 mm，為歷年降水量最低值。1961—2018年，波密站年降水量>1 000 mm的就有12次，而年降水量<500 mm的僅只有3次，分別為1961、1964年和1967年。從月量時間尺度上看，波密站歷年單月降水量>200 mm的就有27次，其中歷年6月降水量>200 mm的就達11次，占2/5。

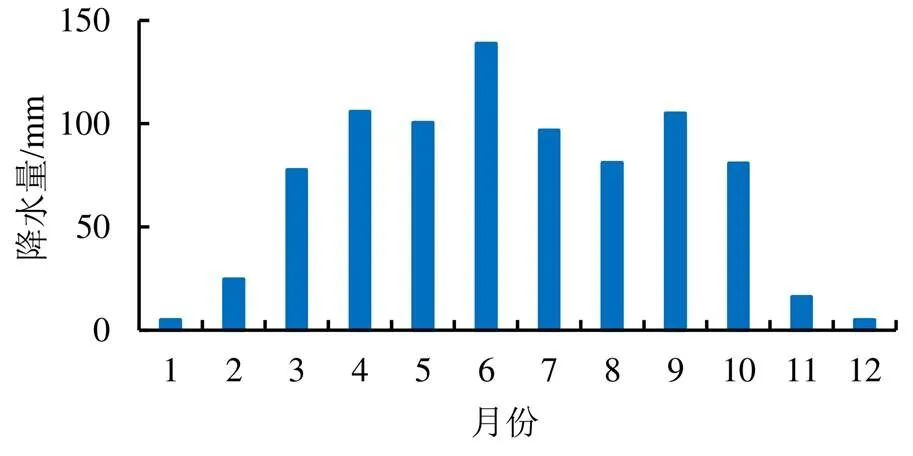
圖1 1961—2018年波密站各月份平均降水量

通過圖1可知，波密站降水主要集中在4—9月，其中6月降水最多；平均月降水量達130 mm以上；而1968年6月單月降水量達307.9 mm。對1961—2018年波密站12個月歷年降水量數據進行趨勢分析，得到圖2所示的各月降水量趨勢圖，從趨勢圖中可以發現，降水量趨勢變化較大的主要集中在4、5、6月和8月這幾個月。從1961—2018年來看，8月趨勢變化最大，趨勢最明顯；8月降水量從總體處于上升趨勢，但在近年來卻呈下降趨勢；而在近年來，5、6月和11月降水量呈下降趨勢，4、9月和10月降水量呈上升趨勢。

圖2 1961—2018年波密站各月份降水量趨勢圖

2 降水量相空間重構及混沌特征識別

由于降水是一個非線性、非穩定的時間序列，可能具有混沌現象。因此，本文首先利用C-C方法求得相空間重構的2個參數時間延遲和嵌入維數；然后對降水量時間序列進行相空間重構，并使用小數據量法求取Lyapunov指數進行混沌特征判別。

2.1 C-C法相空間重構

相空間重構理論(Phase Space Reconstruction Theory)是混沌系統分析中最重要的一步，基本原理是：獲得時間序列中合適的時間間隔?和時間延遲，利用時間延遲技術將時間序列由一維轉換到一個未改變其拓撲結構的相空間中[28-29]。

1）C-C法理論

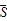
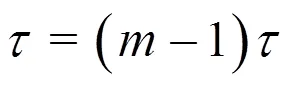
本文計算步驟為[32]：首先將一維降水量時間序列={x|=1,2,…,}分解成個子序列：

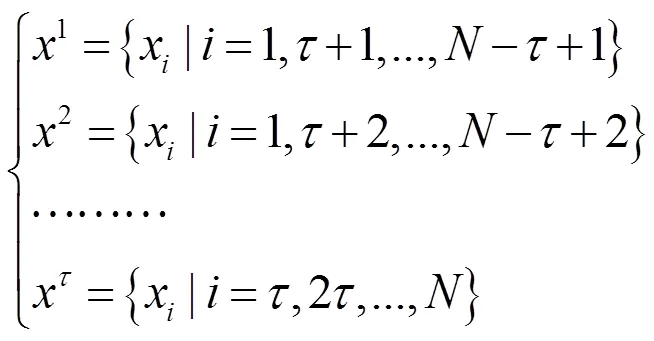
然后計算個子序列：

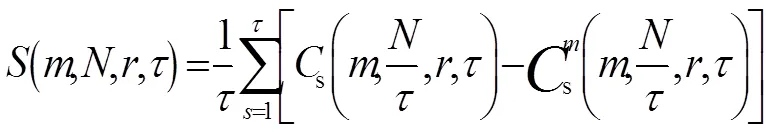
當時，即有：

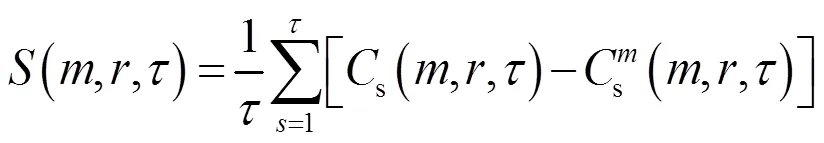
由于降水量時間序列中部分元素還是具有一定相關性，因此(,,)≠0，存在一定的偏差，其最大偏差為：

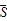
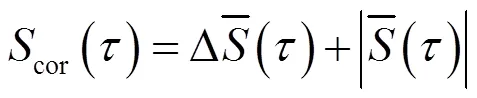
其中，r=/2，=1, 2, 3, 4。

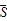
2.2 混沌時間序列判別

本文對波密氣象站1961—2018年歷年12個月的降水量數據，利用C-C算法求取歷年12個月降水量時間序列的時間延遲和嵌入維數，并通過小數據量化求取Lyapunov指數。如表1所示（嵌入維數為四舍五入的整數值）。

表1 波密氣象站12個月混沌理論中的指數

由于波密縣6月降水量以暴雨為主，其降水量時間序列混沌特征較為明顯[33]。并且從表1也可以看出，波密氣象站6月的Lyapunov指數最大，說明該月混沌特征明顯。因此，本文主要以1961—2018年波密氣象站歷年6月降水量數據為例，利用C-C算法求取波密縣1961—2018年歷年6月降水量時間序列的時間延遲和嵌入維數。

一個區域的降水量隨時間是不斷變化的，存在著降水豐富期和降水貧乏期[34]，這可能會導致一些混沌現象的產生。因此，本文利用小數據量法求取最大Lyapunov指數對降水量時間序列進行混沌判別。

圖4 統計量綜合表現圖

設降水量混沌時間序列為{1,2,…,x}，則重構相空間：

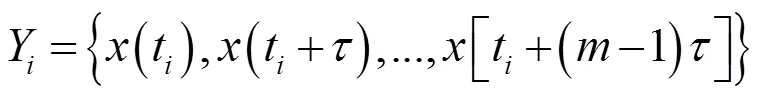
其中為混沌降水量時間序列的平均周期。

求出所有的lnd()平均()，即[36]：

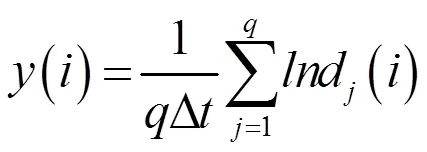
其中為d()≠0時的具體值。

利用最小二乘法求()得到1條回歸直線，其斜率為最大Lyapunov指數即。Lyapunov指數是衡量系統動力學特性中最為重要的指標，其大小直接決定時間序列的混沌程度。若<0時，說明該時間序列具有確定性，可進行長期預測；若>0時，說明該時間序列具有混沌性，可進行短期預測；若=0時，說明該時間序列具有隨機性，預測效果差[37]。

從圖5可以看出>0，說明波密縣6月歷年降水量時間序列存在著混沌性，因此，可以運用混沌理論來分析和預測。

我們研究民俗，不應該僅僅停留在了解民俗事象的來龍去脈，也不能滿足于將民俗事象描述清楚，而是要通過這些民俗事象去了解其背后的實實在在的人，看看這些人是如何借助民俗來組織日常生活的，以及怎樣賦予日常生活以意義的。對話與交流的民俗志，很大程度上就是要把這些過程呈現出來，個人敘事作為呈現這些過程的最為尋常而有力的日常話語形式，就顯得異常重要了。

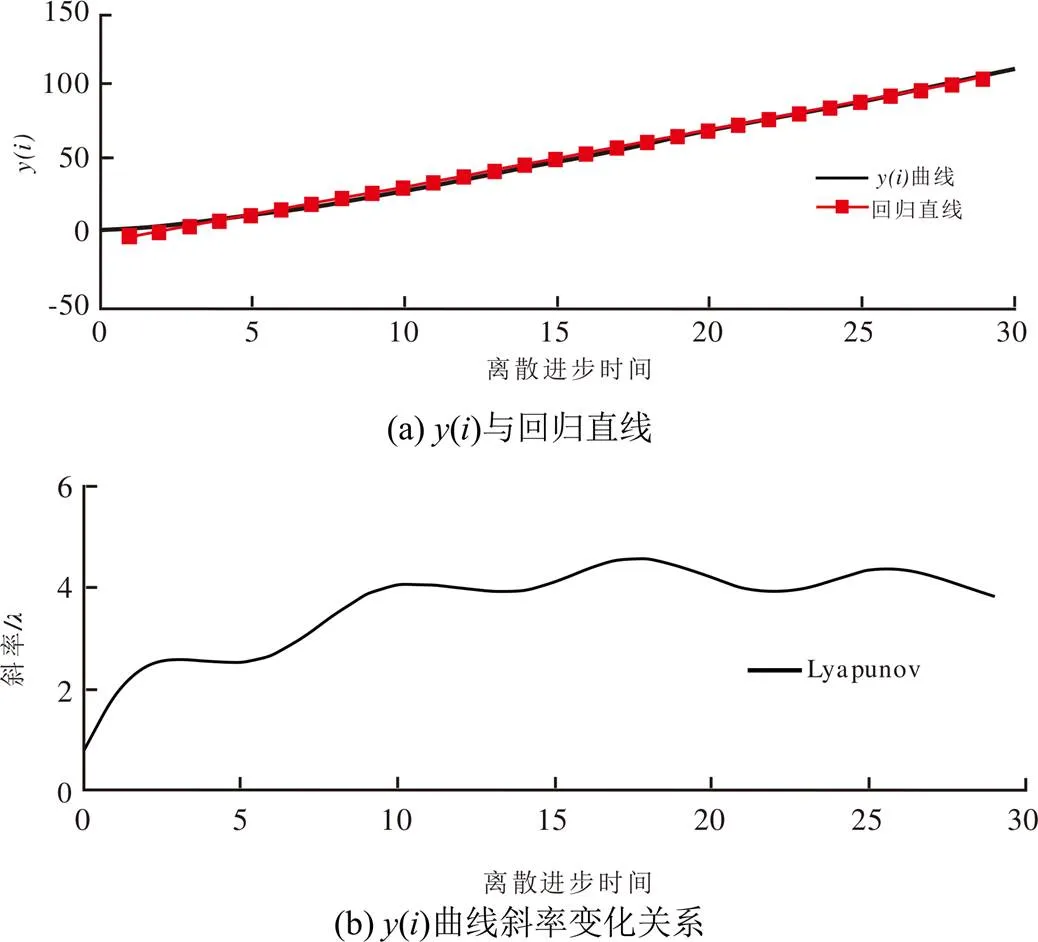
圖5 y(i)與回歸直線關系

3 降水量預測

3.1 Volterra自適應多步預測模型

Volterra級數能很好解決非線性系統中的問題，張家樹等[38]構建了混沌信號非線性自適應預測模型及預測算法，并且該算法已應用于時間序列的預測中。發現當Volterra級數截斷項數取最佳嵌入維數時，時間延遲為時，所構建的二階Volterra自適應預測模型具有很好的預測能力。因此，本文利用C-C算法求取的最小嵌入維數，時間延遲，構建 Volterra混沌降水量多步預測模型。

假設非線性系統中輸入量為降水量時間序列()=[(),(-),…,(-(-1))]，輸出量為()=(+1)，則此Volterra自適應二階濾波模型為：

3.2 降水量預測評價指標

為了評價模型的預測效果，本文引用4個評價指標分別為：平均絕對百分比誤差（）、平均絕對誤差（）、均方誤差（）和均等系數（，即擬合度）[40]。4個評價指標的公式為：

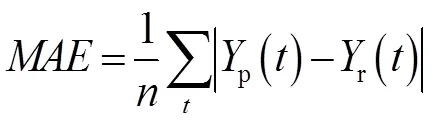
式中：r()為在年降水量實際值；p()表示在年降水量預測值；為預測時段長度。和是反映預測值與實際值之間的誤差大小，而反映預測誤差分別情況，其值越小則說明預測效果越好，值則是反映預測值與實際值之間的擬合程度，其值越大則說明預測效果去實際值的曲線擬合度越高[41]，通常情況下，較好的預測模型其值應大于0.85，若>0.9，則說明該模型具有可用性較高的預測精度。

3.3 預測結果分析

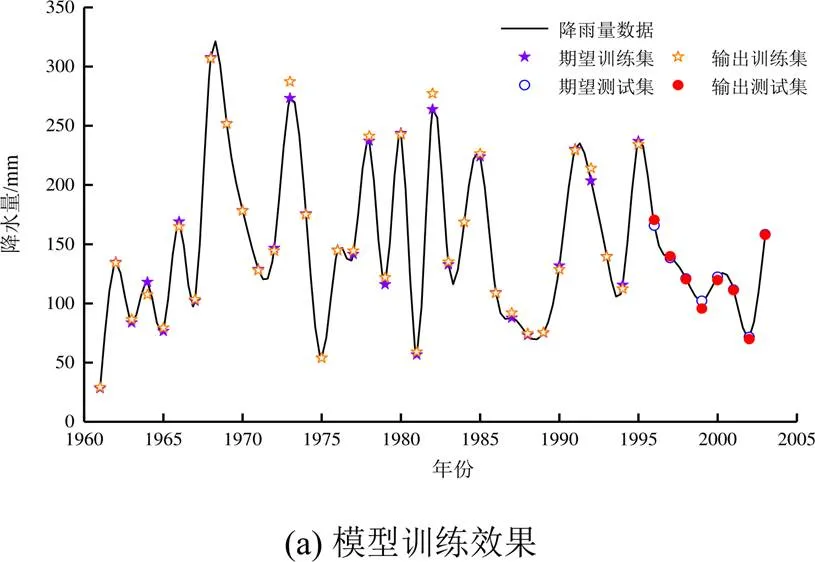
運用Volterra模型對存在混沌特征的降水量進行預測，首先利用C-C法求取嵌入維數和時間延遲，然后依據和對降水量時間序列進行相空間重構，對重構后的時間序列使用Volterra級數分別進行短期5 a預測和長期15 a預測。在長期預測中，利用1961—1995年波密氣象站歷年6月數據作為訓練集，訓練模型；同時用1996—2003年的數據作為測試集，測試模型；預測2004—2018年共15 a歷年6月降水量，并與真實值進行對比。在短期預測中，則是利用1961—2013年波密氣象站歷年6月數據作為訓練集，訓練模型；并預測2014—2018年共5a的6月降水量，同時與真實值進行對比。圖6為模型訓練的誤差自相關圖，相關系數在滯后算子時步為0時取最大，其他情況不超過置信界限時為最佳。圖7為模型訓練效果圖，從圖7可以看出模型的整體訓練效果不錯，訓練集和測試集誤差在5%以內。結合圖6和圖7可以發現，Volterra模型訓練結果較好，完全滿足預測要求。

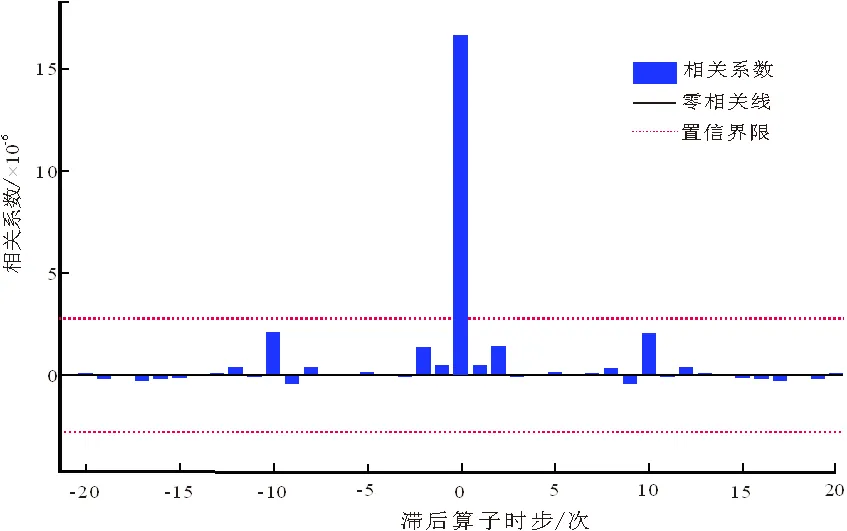
圖6 誤差自相關圖

3.3.1 長期預測：15 a

通過表2和圖8可以分析出，在對混沌特征明顯的降水量進行長期預測時，Volterra模型的預測效果并不是很理想，其預測精度不如SVR模型，但比小波模型精度略高。其為18.318%，為0.901，而卻達69.295。并且隨著預測時間域跨度的增大，其預測誤差變大。

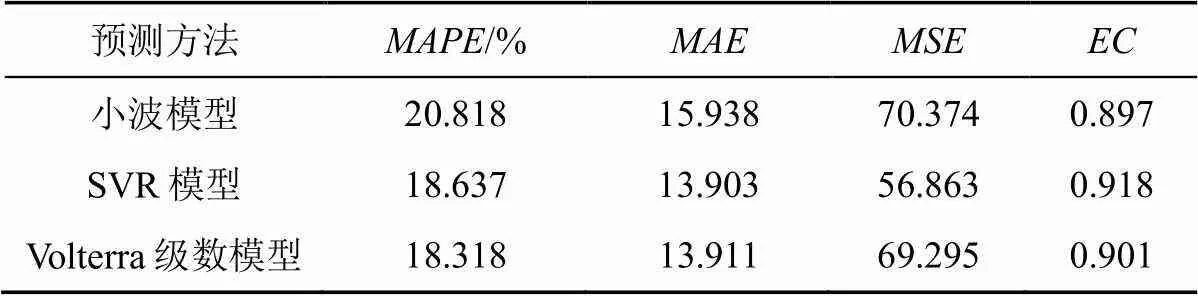
表2 3個預測模型15 a降水量預測性能指標

圖8 長期15 a的3個模型預測值與實際曲線圖

3.3.2 短期預測：5 a

在短期預測中，通過表3和圖9發現，在對具有混沌特征的降水量短期預測時，Volterra預測模型的為0.941，為4.04%，其精度遠遠高于小波模型和SVR模型；說明在具有混沌特征的短期降水量預測中Volterra預測模型具有更高的預測精確度。

表3 3個模型5 a降水量預測性能指標

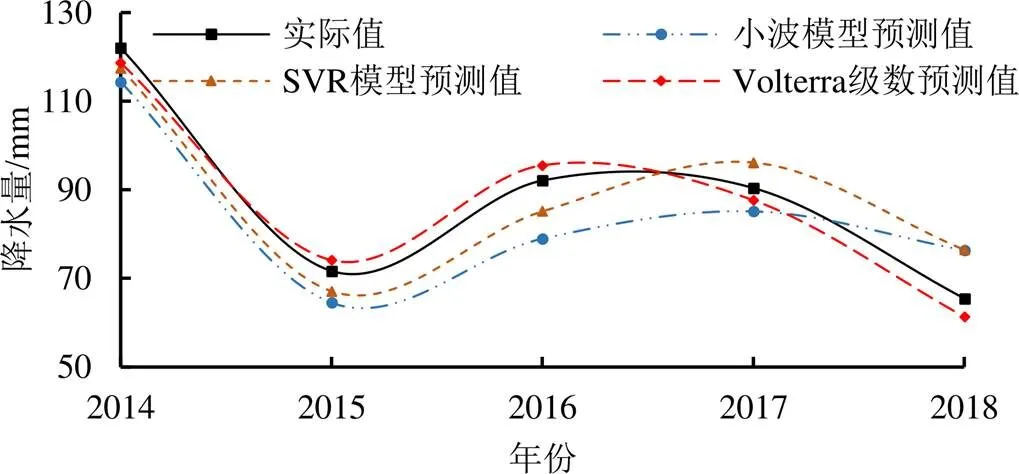
圖9 短期5 a模型預測值與實際曲線圖

3.3.3 疊加預測誤差分析

在降水量預測中，常常會利用預測的降水量來繼續預測后面的降水量，可能造成誤差累計，產生較大的誤差[34]。因此，本文將針對短期預測進行疊加誤差計算分析。為了防止預測模型形成學習記憶，本文選取同樣具有混沌特征的波密氣象站1961—2018年歷年7月降水量，來進行疊加誤差分析，其方法為：先利用1961—2013年7月降水量預測2014年7月降水量，然后再利用1961—2014年7月降水量預測2015年7月降水量，依次疊加預測至2018年7月的降水量。將預測值與實際值進行對比。通過表4可以發現，Volterra模型的疊加預測值相比與小波模型和SVR模型的疊加預測值來說較接近真實值，最大誤差在10 mm以下。

從表5可以看出，在對具有混沌特征的降水量進行短期疊加預測誤差分析，發現Volterra模型的、、和共4個指標參數均優于小波模型和SVR模型，其>0.85，而小波模型的為0.731，SVR模型的為0.803，均小于0.85。說明Volterra模型在短期預測中，降水量疊加預測值不受時間限制，滿足預測值的誤差要求。

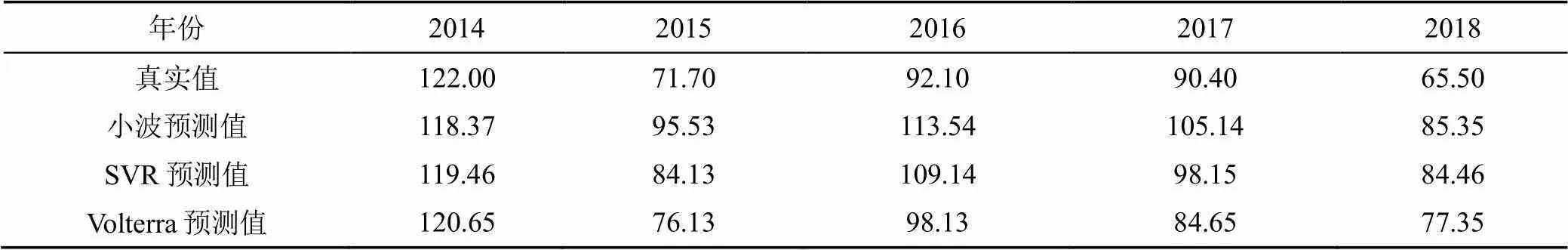
表4 疊加5 a降水量預測值與實際值

表5 3個模型疊加5 a降水量預測性能指標

3.3.4 模型推廣

為了分析Volterra模型在不具備混沌特征的時間序列中，對短期預測能否依然具有高精度預測。通過前文對降水量的混沌特性判斷（表1），發現波密站1、2月和12月混沌特征不明顯，其Lyapunov 指數分別為0.000 17、0.001 10和0.003 20；因此，本文利用1961—2013年2月數據對模型進行推廣分析，利用2014—2018年2月數據進行檢驗。

通過圖10和表6、表7可以發現，在對混沌特征弱的降水量時間序列預測時，Volterra預測模型預測效果不佳，其模型的擬合度只有0.57，并且達到54.9%；而SVR模型卻表現出較高的預測精確度，模型的擬合度達到0.88，只有10.63%，說明在對混沌特征弱的降水量時間序列預測時，SVR模型要優于Volterra模型。

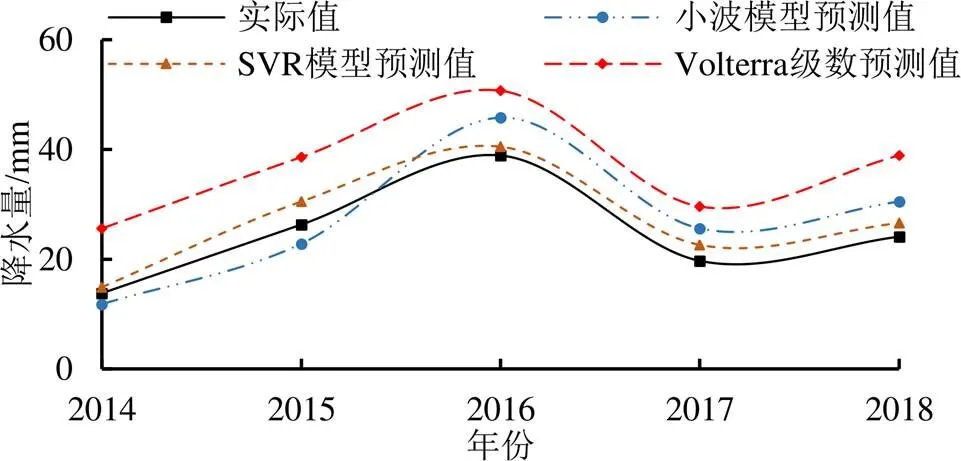
圖10 5 a降水量預測值與實際值曲線圖

表6 預測5 a混沌特征弱的降水量的預測值與實際值

表7 模型預測5 a混沌特征弱的降水量的預測性能指標

4 討 論

降水量時間序列中存在混沌現象[8]。通過對波密氣象站1961—2018年歷年月降水量進行特征分析，利用混沌理論進行混沌特征判別，構建了能較好預測混沌特征的預測模型Volterra，對含混沌特征的月降水量進行長期15 a和短期5 a的預測。經疊加誤差分析及模型推廣分析，并與小波預測模型和SVR預測模型對比，發現該模型能夠對短期5 a內的混沌月降水量進行較高精度的預測，但對長期15 a內的混沌月降水量預測效果并不如SVR模型，這主要是因為Volterra模型多步預測機制和研究區域所處環境共同決定。

一方面，Volterra模型進行多步預測與小波模型和SVR模型不同，其預測機制是通過利用已知月降水量在模型的濾波系統中進行訓練，在訓練好的模型中預測出一個預測值；然后將其預測出來的預測值，繼續輸入到訓練好的模型中進行下一次預測，依次迭代出多個預測值。因此，在這個過程中會出現疊加預測誤差的影響，隨著預測尺度的加長，該模型的預測誤差便會突顯出來。故Volterra模型在長期預測中預測效果低于其他模型[39]；而SVR模型在長期預測中由于該模型中核函數和懲罰因子根據預測值不斷優化模型，從而在長期預測中效果較好；但在短期預測中，由于預測值樣本數量少，導致SVR模型中核函數和懲罰因子還未完全優化好模型，因此在短期模型中預測效果差[37]。小波模型則是通過小波分解將月降水量數據分解成多層小波系數，然后對各層小波系數進行預測，最后對預測的小波系數進行重構[3]；而通過混沌理論分析的降水量本身就具有了多維性，若再進行小波分解，則導致誤差被進一步擴大，因而小波模型對混沌特征的降水量進行預測的效果不佳。

而另一方面，由于研究區域所處青藏高原地區，歷年月降水變化差異較大，進行長期預測難度較大，并且預測精度也不理想[42]。

雖然利用Volterra模型能夠提高具有混沌特征月降水量預測精度，但本研究仍存在一些不足。首先，本研究選取的研究區域太局限，只局限于波密氣象站，還需要利用其他地區的氣象站數據進行進一步適用性研究。此外，Volterra預測模型主要廣泛應用于氣溫[39]等領域，而且較少應用于降水量預測，在降水量預測中還需進一步深入研究。

5 結 論

1）利用C-C法求取波密站1961—2018年12個月的降水量時間序列的時間延遲和嵌入維數，并用小數據量法求取12個月的Lyapunov指數()，通過Lyapunov指數發現：波密氣象站6月份降水量混沌特征最明顯，其=2.674 5；而1、2、12月混沌特征較弱，分別為0.000 17、0.001 10、0.003 20。

2）通過利用Volterra混沌降水量預測模型進行短期5 a和長期15 a預測，將其預測值與小波模型和SVR模型預測值對比分析發現：Volterra預測模型在短期5 a預測中，預測精度高于小波模型和SVR模型，其=4.04%；=0.941，但在長期15 a預測中，預測精度低于SVR模型，其=18.318%，=0.901。

3）在Volterra模型進行疊加預測誤差和推廣分析時發現：Volterra預測模型對混沌特性明顯的降水量短期預測時，=0.89，能夠滿足降水量不斷疊加預測的要求；Volterra預測模型對混沌特征弱的降水量短期預測時，其預測精度比小波預測模型和SVR預測模型精度都低，只有0.566，不能達到預測要求。

[1] 高澤民, 丁明濤, 楊國輝, 等. 川藏鐵路孜熱—波密段泥石流災害危險性評價[J]. 工程地質學報, 2021, 29(2): 478-485.

GAO Zemin, DING Mingtao, YANG Guohui, et al. Hazard assessment of debris flow along Zire-Bomi section of Sichuan-Tibet railway[J]. Journal of Engineering Geology, 2021, 29(2): 478-485.

[2] 王志良, 張永山. 昆明年降雨量時間序列的混沌分析[J]. 華北水利水電學院學報, 2011, 32(2): 8-10.

WANG Zhiliang, ZHANG Yongshan. Chaos analysis of time series of Kunming annual precipitation[J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2011, 32(2): 8-10.

[3] 金玉婷. 基于混沌和小波神經網絡的短時交通流預測方法研究[D].成都: 西南交通大學, 2014.

JIN Yuting. Research on short-term traffic flow forecasting method based on chaos and wavelet neural network[D]. Chengdu: Southwest Jiaotong University, 2014.

[4] 曹秀佳, 谷健, 馬寧寧, 等. 基于粒子群優化小波神經網絡模型的春玉米生育階段干旱預測[J]. 灌溉排水學報, 2021, 40(3): 125-133.

CAO Xiujia, GU Jian, MA Ningning, et al. Predicting droughts in growth season of spring maize with the wavelet neural networks using particle swarm optimization training[J]. Journal of Irrigation and Drainage, 2021, 40(3): 125-133.

[5] LORENZ E N. Deterministic Nonperodic Flow [J]. Journal of the Atmospheric Sciences, 1963, 20: 130-141.

[6] HENSE A. On the Possible Existence of a Strange Attractor for the Southern Oscillation[J]. Beitr Phys Atmos, 1987, 60(1): 34-37.

[7] SIVAKUMAR B, LIONG S Y, LIAW CY. Evidence of Chaotic Behavior in Singapore Rainfall[J]. Journal of the American Water Resources Association, 1998, 34(2): 301-310.

[8] 袁鵬, 李謂新, 王文圣, 等. 月降雨量時間序列中的混沌現象[J]. 四川大學學報(工程科學版), 2002(1): 16-19.

YUAN Peng, LI Weixin, WANG Wensheng, et al. Chaos analysis of monthly precipitation time series[J]. Journal of Sichuan University (Engineering Science), 2002(1): 16-19.

[9] 王紅瑞, 宋宇, 劉昌明, 等. 混沌理論及在水科學中的應用于存在的問題[J]. 水科學進展, 2004, 15(3): 400-407.

WANG Hongrui, SONG Yu, LIU Changming, et al. Application and issues of chaos theory in hydroscience[J]. Advances in Water Science, 2004, 15(3): 400-407.

[10] 王文, 許武成. 對水文時間序列混沌特征參數估計問題的討論[J]. 水科學進展, 2005(4): 609-616.

WANG Wen, XU Wucheng. Some issues on the characterization of chaotic properties of hydrologic time series[J]. Advances in Water Science, 2005(4): 609-616.

[11] SIVAKUMAR B, BERNNDTSSON R, PERSSON M. Monthly runoff prediction using phase-space reconstruction[J]. Hydrological Sciences Journal. 2001, 46(3): 377-388.

[12] 石教智, 陳曉宏, 林汝顏. 東江流域降水時間序列的混沌特征分析[J]. 中山大學學報(自然科學版), 2006(4): 111-115.

SHI Jiaozhi, CHEN Xiaohong, LIN Ruyan. Chaotic characteristics of precipitation time series in the Dongjiang river valley[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2006(4): 111-115.

[13] 梁婕, 曾光明, 郭生練, 等. 洞庭湖區月降雨序列的混沌特性識別及預測研究[J]. 水電能源科學, 2006(5): 16-19, 98.

LIANG Jie, ZENG Guangming, GUO Shenglian, et al. Diagnosis of chaotic behavior and forecast resources for monthly rainfall in Dongting lake area[J]. Water Resources and Power, 2006(5): 16-19, 98.

[14] 趙文剛, 馬孝義, 劉曉群, 等. 基于神經網絡算法的廣東省典型代表站點0簡化計算模型研究[J]. 灌溉排水學報, 2019, 38(5): 91-99.

ZHAO Wengang, MA Xiaoyi, LIU Xiaoqun, et al. Using neural network model to simplify0calculation for representative stations in Guangdong province[J]. Journal of Irrigation and Drainage, 2019, 38(5): 91-99.

[15] CHAITANTA D, ALI Y. Flood prediction using time series data mining[J]. Journal of Hydrology. 2007, 333: 305-316.

[16] 計亞麗, 賈克力, 韓璞璞. 基于LS-SVM和RBF的月降雨混沌時間序列預測[J]. 水電能源科學, 2012, 30(9): 13-16, 214.

JI Yali, JIA Keli, HAN Pupu. Prediction of monthly rainfall chaotic time series based on LS-SVM and RBF model[J]. Water Resources and Power, 2012, 30(9): 13-16, 214.

[17] DE DOMENICO M, GHORBANI M A, MAKARYNSKYY O, et al. Chaos and Reproduction in Sea Level[J]. Applied Mathematical Modelling, 2013, 37(6): 3 687-3 697.

[18] 喬雨, 閆佰忠, 梁秀娟, 等. 黑龍江省降水混沌識別及空間分布研究[J]. 水文, 2015, 35(3): 64-68.

QIAO Yu, YAN Baizhong, LIANG Xiujuan, et al. Identification and spatial distribution for chaos of precipitation in Heilongjiang province[J]. Journal of China Hydrology, 2015, 35(3): 64-68.

[19] WANG W C, CHAU K W, XU D M, et al. Improving forecasting accuracy of annual runoff time series using ARIMA based on EEMD decomposition[J]. Water Resources Management, 2015, 29(8): 2 655-2 675.

[20] ZOUNEMAT-KERMANI M. Investigating Chaos and Nonlinear Forecasting in Short Term and Mid-term River Discharge[J]. Water Resources Management, 2016, 30(5): 1 851-18 65.

[21] GHORBANI M A, KHATIBI R, MEHR A D, et al. Chaos-based multigene genetic programming: A new hybrid strategy for river flow forecasting[J]. Journal of Hydrology, 2018, 562: 455-467.

[22] 王懷軍, 潘瑩萍, 馮如, 等. 基于空間貝葉斯層次模型的淮河流域氣象極值特征分析[J]. 灌溉排水學報, 2020, 39(5): 102-110.

WANG Huaijun, PAN Yingping, FENG Ru, et al. Using spatial Bayesian hierarchical model to analyze extreme climate indexes in Huai river basin[J]. Journal of Irrigation and Drainage, 2020, 39(5): 102-110.

[23] 康傳利, 陳洋, 張臨煒, 等. 小波和混沌神經網絡在大壩變形預測中的應用[J]. 人民黃河, 2020, 42(3): 101-104, 116.

KANG Chuanli, CHEN Yang, ZHANG Linwei, et al. Application of the wavelet and chaos neural network for monitoring dam deformation[J]. Yellow River, 2020, 42(3): 101-104, 116.

[24] 林祥志, 郭慧芳. 基于小波ANFIS的諸暨站降雨量預測模型[J]. 灌溉排水學報, 2019, 38(S2): 123-125.

LIN Xiangzhi, GUO Huifang. Rainfall prediction model of Zhuji station based on wavelet ANFIS[J]. Journal of Irrigation and Drainage, 2019, 38(S2): 123-125.

[25] 馮兆宇, 崔天時, 張志強, 等. 基于灰色神經網絡與模糊控制的寒地水稻灌溉制度[J]. 灌溉排水學報, 2018, 37(4): 71-79.

FENG Zhaoyu, CUI Tianshi, ZHANG Zhichao, et al. Calculating irrigation schedule for rice in temperate regions using a combination of grey neural network and fuzzy control[J]. Journal of Irrigation and Drainage, 2018, 37(4): 71-79.

[26] 趙自陽, 王紅瑞, 趙巖, 等.基于混沌理論的漢江上游安康站1950—2014年逐月降水量特征[J]. 長江科學院院報, 2021, 38(7): 137-142.

ZHAO Ziyang, WANG Hongrui, ZHAO Yan, et al. Analysis of monthly precipitation characteristics of Ankang station on upper Hanjiang river from 1950 to 2014 based on chaos theory[J]. Journal of Yangtze River Scientific Research Institute, 2021, 38(7): 137-142.

[27] 肖章玲, 梁忠民, 李彬權, 等. 一種基于混沌理論的“量”-“型”相似預測模型[J]. 南水北調與水利科技(中英文), 2021, 19(5): 894-899, 929.

XIAO Zhangling, LIANG Zhongmin, LI Binqun, et al. A quantity-pattern similarity predictive model based on chaos theory[J]. South-to-North Water Transfers and Water Science & Technology, 2021, 19(5): 894-899, 929.

[28] PACKARDH N, CRUTCHFIELD J P, Farmer J D, et al. Geometry from a Time Series[J]. Physical Review Letters, 1980, 45(9): 712-716.

[29] TAKENS F. Detecting strange attractors in turbulence[J]. Lecture Notes in Mathematics, 1981, 898: 366-381.

[30] 陸振波, 蔡志明, 姜可宇. 基于改進的C-C方法的相空間重構參數選擇[J]. 系統仿真學報, 2007(6): 2 527-2 538.

LU Zhenbo, CAI Zhiming, JIANG Keyu. Determination of embedding parameters for phase space reconstruction based on improved C-C method[J]. Journal of System Simulation, 2007(6): 2 527-2 538.

[31] SERGIU B. The Roller-Ground Dynamic Interaction in the Compaction Process Through Vibrations for Road Construction[J]. Romanian Journal of Transport Infrastructure, 2016, 5(2): 1-9.

[32] 張旭濤, 賀國光, 盧宇. 一種在線實時快速地判定交通流混沌的組合算法[J]. 系統工程, 2005(9): 46-49.

ZHANG Xutao, HE Guoguang, LU Yu. A combined algorithm for real-time on-line rapid identification of the chaos in traffic flow[J]. Systems Engineering, 2005(9): 46-49.

[33] 王海科, 李亞斌, 錢會. 西安市可利用降水量特征分析及預測[J]. 灌溉排水學報, 2017, 36(12): 118-122.

WANG Haike, LI Yabin, QIAN Hui. Analyzing and predicting the applicable precipitation in Xi'an city[J]. Journal of Irrigation and Drainage, 2017, 36(12): 118-122.

[34] 舒濤, 葉唐進, 李俊杰, 等. 降雨量及疊加預測方法研究[J]. 高原氣象, 2021, 40(1): 169-177.

SHU Tao, YE Tangjin, LI Junjie, et al. Analysis of prediction method for rainfall and superposition rainfall[J]. Plateau Meteorology, 2021, 40(1): 169-177.

[35] 高允報, 孫玉泉. 計算Lyapunov指數的模糊C均值聚類小數據量法[J]. 東北師大學報(自然科學版), 2021, 53(1): 38-42.

GAO Yunbao, SUN Yuquan. A small data method for calculating Lyapunov exponent using fuzzy C-means clustering[J]. Journal of Northeast Normal University (Natural Science Edition), 2021, 53(1): 38-42.

[36] 孫義, 黃顯峰. 基于最大Lyapunov指數的混沌預測在洪水實時預報中的應用[J]. 水利水電技術, 2016, 47(1): 102-106.

SUN Yi, HUANG Xianfeng. Application of maximun Lyapunov index-based chaotic forecasting method to real-time flood forecast[J]. Water Resources and Hydropower Engineering, 2016, 47(1): 102-106.

[37] 劉婷婷, 史久根, 韓江洪. 基于SVM的瓦斯體積分數混沌時間序列預測[J]. 合肥工業大學學報(自然科學版), 2009, 32(8): 1 150-1 153.

LIU Tingting, SHI Jiugen, HAN Jianghong. Prediction of gas concentration chaotic time series based on support vector machines[J]. Journal of Hefei University of Technology (Natural Science), 2009, 32(8): 1 150-1 153.

[38] 張家樹, 肖先賜. 混沌時間序列的Volterra自適應預測[J]. 物理學報, 2000, 49(3): 403-408.

ZHANG Jiashu, XIAO Xianci. Predicting low-dimensional chaotic time series using Volterra adaptive filers[J]. Acta Physica Sinica, 2000, 49(3): 403-408.

[39] 何鮮峰, 汪自力, 何啟, 等. 基于相空間重構和Volterra的非線性寒區氣溫預測方法[J]. 中國科學(技術科學), 2019, 49(6): 733-740.

HE Xianfeng, WANG Zili, HE Qi, et al. The cold regions' temperature nonlinear prediction method basing on phase space reconstruction and Volterra filter[J]. Scientia Sinica (Technologica), 2019, 49(6): 733-740.

[40] 宋剛, 張云峰, 包芳勛, 等. 基于粒子群優化LSTM的股票預測模型[J]. 北京航空航天大學學報, 2019, 45(12): 2 533-2 542.

SONG Gang, ZHANG Yunfeng, BAO Fangxun, et al. Stock prediction model based on particle swarm optimization LSTM[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(12): 2 533-2 542.

[41] 孫朝東,梁雪春. 改進的花授粉算法優化SVM在交通流中的應用[J].計算機工程與設計, 2016, 37(10): 2 717-2 721.

SUN Chaodong, LIANG Xuechun. Application of improved flower pollination algorithm optimized support vector machine in short-term traffic flow[J]. Computer Engineering and Design, 2016, 37(10): 2 717-2 721.

[42] 馬偉東, 劉峰貴, 周強, 等. 1961—2017年青藏高原極端降水特征分析[J]. 自然資源學報, 2020, 35(12): 3 039-3 050.

MA Weidong, LIU Fenggui, ZHOU Qiang, et al. Characteristics of extreme precipitation over the Qinghai-Tibet Plateau from 1961 to 2017[J]. Journal of Natural Resources, 2020, 35(12): 3 039-3 050.

Predicting Monthly Precipitation Using Chaotic Model

SHU Tao1, LU Haotian2, CAO Jingxuan3, YE Tangjin4, TAO Wei3, FU Runyi3, LI Hao5,6,7*

(1.College of Marine Geosciences, Ocean University of China, Qingdao 266100, China; 2.College of Earth Sciences, Guilin University of Technology, Guilin 541004, China; 3.College of Engineering, Tibet University, Lhasa 850000, China; 4. Department of Construction Engineering,Dalian University of Technology, Dalian 116024, China; 5. Key Laboratory of Mountain Hazards and Earth Surface Process,Chinese Academy of Sciences, Chengdu 610041, China; 6. Institute of Mountain Hazards and Environment,Chinese Academy of Sciences ＆ Ministry of Water Conservancy, Chengdu 610041, China; 7.University of Chinese Academy of Sciences, Beijing 100049, China)

【】The time series of rainfall is a nonlinear, non-stationary process and can be analyzed statistically. The purpose of this paper is to analyze the chaotic characteristics of rainfalls in attempts to develop a chaotic model to predict monthly precipitation.【】We took monthly precipitation measured from the weather station at Bomi between Linzhi and Bomi on the G318 highway as an example, the C-C correlation integral method was used to determine the delay timeand the embedding dimensionin itThe time series was then reconstructed in phase space whose Lyapunov exponent was obtained for a small sub-dataset to determine the chaotic characteristics, from which we constructed a Volterra model to predict monthly rainfall in both short-term (5 years) and long-term (15 years) respectively. The predicted monthly rainfalls using the proposed model were compared with those predicted by the wavelet model and the SVR prediction model.【】Theandof the rainfalls predicted using the proposed Volterra model for short-term was 4.04% and 0.941 respectively. Compared with the wavelet and SVR model, the proposed Volterra model was more accurate, and its superposition prediction error was smaller, with its associatedandbeing 7.657% and 0.894 respectively. However, the rainfalls predicted by the proposed for long-term were not as good as those by the SVR model. When the time series of the rainfall was less chaotic, the prediction of Volterra model for short-term rainfall was less reliable, with its associatedandbeing 54.855% and 0.566, respectively.【】The chaotic model was more accurate than the traditional model for predicting monthly rainfall only for short-term and when the time series of the rainfalls is chaotic. Therefore, it should be used with care.

chaotic model; phase space reconstruction; lyapunov index; volterra filter; rainfall prediction

2021-08-24

廣西研究生教育創新計劃項目（YCSW2021203）；大學生創新實驗項目（202010694008）；大學生創新實驗項目（2020XCX011）

舒濤（1998-），男，湖南麻陽人。碩士研究生，主要從事大數據分析及數值模擬分析。E-mail: stwho_1998@163.com.

李豪（1997-），男，四川眉山人。博士研究生，主要從事泥石流地貌研究。E-mail: leeho97@163.com.

1672 - 3317（2022）03 - 0083 - 09

P457；P208

A

10.13522/j.cnki.ggps.2021385

舒濤, 路昊天, 曹景軒, 等. 基于混沌理論的降水量預測方法研究[J]. 灌溉排水學報, 2022, 41(3): 83-91.

SHU Tao, LU Haotian, CAO Jingxuan, et al. Predicting Monthly Precipitation Using Chaotic Model[J]. Journal of Irrigation and Drainage, 2022, 41(3): 83-91.

責任編輯：趙宇龍