基于關(guān)鍵數(shù)字特征的風(fēng)險(xiǎn)資產(chǎn)組合理論及實(shí)證分析研究

范國兵， 袁 濤

(湖南財(cái)政經(jīng)濟(jì)學(xué)院 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，湖南 長沙 410205)

0 引言

金融市場中，二級流通市場的各項(xiàng)證券投資都具有一定的風(fēng)險(xiǎn)，然而各項(xiàng)投資的風(fēng)險(xiǎn)程度以及風(fēng)險(xiǎn)最終出現(xiàn)的可能性并不一致。MARKOWITZ H M用投資收益的不確定性描述風(fēng)險(xiǎn)資產(chǎn)投資的風(fēng)險(xiǎn)表征[1]，其風(fēng)險(xiǎn)的不確定性影響較為廣泛。風(fēng)險(xiǎn)源的多樣性以及風(fēng)險(xiǎn)擴(kuò)散機(jī)制都是資本市場極為關(guān)注的，以數(shù)學(xué)特征的表達(dá)方式進(jìn)行分析風(fēng)險(xiǎn)資產(chǎn)投資組合經(jīng)濟(jì)效率與盈虧率。在此之后，眾多研究都在不斷地豐富和完善現(xiàn)有的風(fēng)險(xiǎn)資產(chǎn)投資組合理論，尤其以均值方差的均衡分析實(shí)現(xiàn)收益和風(fēng)險(xiǎn)之間的最佳平衡，從而服務(wù)于理性投資者所追求的投資決策。關(guān)于證券投資市場的主要研究，股票市場及其靈活的融資方式與多樣性的風(fēng)險(xiǎn)因素，是風(fēng)險(xiǎn)資產(chǎn)投資組合最主要的研究主體[2]。在證券交易的過程中，進(jìn)行理論性的總結(jié)和經(jīng)驗(yàn)性的認(rèn)識，從中把握量化分析思維，借助數(shù)字特征分析的優(yōu)勢決定資產(chǎn)配置模型的有效性。

1 風(fēng)險(xiǎn)資產(chǎn)組合測度分析

MARKOWITZ H M通過均值方差模型進(jìn)行投資組合的研究，以分析單目標(biāo)下的二次規(guī)劃，實(shí)現(xiàn)風(fēng)險(xiǎn)投資組合的最優(yōu)化配置，為風(fēng)險(xiǎn)資產(chǎn)配置組合理論開了數(shù)字特征的先河[3]。

目標(biāo)函數(shù)

其中σ2(p)表示風(fēng)險(xiǎn)資產(chǎn)的方差；Xi、ri分別表示第i種風(fēng)險(xiǎn)資產(chǎn)的權(quán)重配比與收益率。

約束條件

其中E(Rp)表示由風(fēng)險(xiǎn)資產(chǎn)所構(gòu)成的證券投資組合的期望收益率；E(Ri)表示單個(gè)風(fēng)險(xiǎn)資產(chǎn)的期望收益率。

在風(fēng)險(xiǎn)資產(chǎn)組合與無風(fēng)險(xiǎn)資產(chǎn)間的投資組合之中，以關(guān)鍵數(shù)字特征的基本分析，分析股票組合風(fēng)險(xiǎn)變動規(guī)律，在簡化Markowitz模型的基礎(chǔ)上，進(jìn)行兩證券資產(chǎn)配置分析模型的數(shù)字特征評價(jià)[4]。

1.1 預(yù)期收益的分析描述

期望收益值是在不同情景下，收益率已發(fā)生概率為權(quán)重的加權(quán)平均值，用隨機(jī)變量的數(shù)學(xué)期望描述和反映平均投資收益，數(shù)學(xué)期望越大，期望收益率就越高。從離散型變量著手，分析影響投資組合的隨機(jī)因素，轉(zhuǎn)化為可連續(xù)化的收益結(jié)果，直觀表現(xiàn)出在不同情景下的概率情況與預(yù)期回報(bào)情況，描述投資組合的整體期望。

單個(gè)風(fēng)險(xiǎn)資產(chǎn)的期望收益率記作

證券投資組合的期望收益率記作

投資者根據(jù)投資期限的選擇，得到時(shí)間加權(quán)的平均收益率。當(dāng)收益率波動增大時(shí)，兩種平均方法便會存在顯著的差異，如果收益服從正態(tài)分布，則預(yù)期差異為分布方差的1/2。在度量風(fēng)險(xiǎn)資產(chǎn)的歷史收益時(shí)，通常采用幾何平均數(shù)，估計(jì)未來表現(xiàn)時(shí)通常使用算術(shù)平均數(shù)。未來的投資收益結(jié)果通常包含了許多不確定性，這些不確定性對于未來的財(cái)富影響較大，正是由于這種非對稱性的存在，幾何平均是對未來平均收益的低估，當(dāng)假設(shè)風(fēng)險(xiǎn)資產(chǎn)收益服從正態(tài)分布時(shí)，被低估部分恰好就是方差的一半，可以采用算術(shù)平均的數(shù)字特征糾正這種誤差。

兩者關(guān)系為

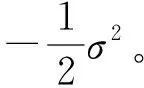
1.2 風(fēng)險(xiǎn)情況的分析描述

在預(yù)期收益的均值分析中，隨機(jī)變量的預(yù)期性差異均是由自生性質(zhì)所導(dǎo)致的，基于此，離散程度的偏移，為風(fēng)險(xiǎn)資產(chǎn)投資組合理論的風(fēng)險(xiǎn)狀況的描述提供了主要依據(jù)[5]。根據(jù)收益率的標(biāo)準(zhǔn)差度量風(fēng)險(xiǎn)，數(shù)值大小用以反映其結(jié)果波動性強(qiáng)度，描述多種不確定性事件的發(fā)生，可以衡量實(shí)際收益和預(yù)期收益之間的偏差，因此方差和均值提供了測量結(jié)果不確定性的方法。

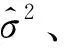
σ2=∑p(s)[r(s)-E(s)]2，

(1)

(2)

(3)

1.3 投資組合相關(guān)性風(fēng)險(xiǎn)描述

在數(shù)字表達(dá)中，協(xié)方差描述兩個(gè)風(fēng)險(xiǎn)資產(chǎn)組合中各個(gè)資產(chǎn)的風(fēng)險(xiǎn)之間相關(guān)關(guān)系下的組合風(fēng)險(xiǎn)，相關(guān)系數(shù)即各個(gè)風(fēng)險(xiǎn)資產(chǎn)間的相關(guān)關(guān)系的大小。如果協(xié)方差為負(fù)，則組合的方差會降低,即使協(xié)方差為正，組合標(biāo)準(zhǔn)差仍低于兩個(gè)證券標(biāo)準(zhǔn)差的加權(quán)平均，除非這兩個(gè)證券是完全正相關(guān)的[6]。它們之間具有關(guān)系式

Cov(r1,r2)=ρ12σ1σ2，

因此在相關(guān)系數(shù)較高時(shí)，組合方差就較高。當(dāng)兩個(gè)資產(chǎn)完全正相關(guān)時(shí)，即相關(guān)系數(shù)等于1時(shí)，組合標(biāo)準(zhǔn)差就是兩個(gè)收益完全正相關(guān)資產(chǎn)標(biāo)準(zhǔn)差的加權(quán)平均，

或

σp=w1σ1+w2σ2。

在其他條件下，相關(guān)系數(shù)小于1時(shí)，組合標(biāo)準(zhǔn)差小于兩個(gè)資產(chǎn)標(biāo)準(zhǔn)差的加權(quán)平均。

2 實(shí)證分析

通過最優(yōu)風(fēng)險(xiǎn)資產(chǎn)組合的兩證券資產(chǎn)配置分析模型進(jìn)行情景模擬，計(jì)算一個(gè)包含兩種風(fēng)險(xiǎn)資產(chǎn)的投資組合的收益率與風(fēng)險(xiǎn)，在模型估計(jì)中計(jì)算不同資產(chǎn)權(quán)重下投資組合的收益率和風(fēng)險(xiǎn)，根據(jù)圖像的生成，可以在一個(gè)目標(biāo)收益率中進(jìn)行無風(fēng)險(xiǎn)資產(chǎn)和最優(yōu)風(fēng)險(xiǎn)資產(chǎn)投資的最優(yōu)選擇。

2.1 數(shù)據(jù)選擇與依據(jù)

以滬深股市的典型行業(yè)為選擇依據(jù)，選取三一重工(即Security 1)與貴州茅臺(即Security 2)，形成兩組風(fēng)險(xiǎn)證券，根據(jù)道氏理論進(jìn)行技術(shù)分析，選取每只股票的每月收盤價(jià)格作為主要的數(shù)據(jù)依據(jù)，期限跨度為14年，從2008年1月至2021年7月的月均收盤價(jià)，以中長期的價(jià)格反映風(fēng)險(xiǎn)資產(chǎn)情況(即股票價(jià)格)，形成多維的股票價(jià)格序列，以跨期的時(shí)間價(jià)格進(jìn)行配置證券組合資本中的風(fēng)險(xiǎn)資產(chǎn)。關(guān)于無風(fēng)險(xiǎn)資產(chǎn)的選擇，以違約概率最低的國債作為無風(fēng)險(xiǎn)資產(chǎn)的配置分析，選取一年期國債收益率進(jìn)行無風(fēng)險(xiǎn)資產(chǎn)的分析。在資產(chǎn)組合的配置中以市場中歷史價(jià)格因素，分析預(yù)期收益、風(fēng)險(xiǎn)程度以及權(quán)重配置比之間的內(nèi)在關(guān)系，以較為理想化的證券市場環(huán)境以及證券性質(zhì)，分析資本資產(chǎn)的配置組合。

2.2 數(shù)據(jù)分析

關(guān)于風(fēng)險(xiǎn)資產(chǎn)的數(shù)字特征，以歷史數(shù)據(jù)信息分析均值情況，首先對收益率的序列特征進(jìn)行處理，即r=ln(Pt/Pt-1)，得到風(fēng)險(xiǎn)資產(chǎn)的收益情況，然后進(jìn)行數(shù)據(jù)處理，利用算術(shù)平均值的計(jì)算方式描述風(fēng)險(xiǎn)資產(chǎn)的均值情況。基于此，進(jìn)行風(fēng)險(xiǎn)資產(chǎn)的方差計(jì)算，以較為明確的風(fēng)險(xiǎn)特征，進(jìn)行組合配置的分析，生成兩組風(fēng)險(xiǎn)資產(chǎn)的收益情況、標(biāo)準(zhǔn)差以及相關(guān)系數(shù)。在Excel的輔助計(jì)算中，以VARP函數(shù)得到風(fēng)險(xiǎn)資產(chǎn)的方差，用以進(jìn)一步描述風(fēng)險(xiǎn)特征，再對其開平方得到標(biāo)準(zhǔn)差。在兩組的風(fēng)險(xiǎn)資產(chǎn)中，通過用COVAR和CORREL函數(shù)得到相應(yīng)的相關(guān)系數(shù)與協(xié)方差[7](如表1所示，數(shù)據(jù)來源為2008—2021年三一重工、貴州茅臺以及中國一年期國債收益率數(shù)據(jù)信息[8-10])。

表1 風(fēng)險(xiǎn)與收益特征描述Tab.1 Description of risk and return characteristics

無風(fēng)險(xiǎn)資產(chǎn)的配置以一年短期國債表示，通過原有的年化收益率轉(zhuǎn)化為每月收益率，經(jīng)數(shù)據(jù)處理之后，可使用統(tǒng)一時(shí)間口徑的收益率比較。承接表1數(shù)據(jù)進(jìn)行風(fēng)險(xiǎn)資產(chǎn)的配置組合，再結(jié)合各權(quán)重變量的調(diào)整，在風(fēng)險(xiǎn)資產(chǎn)與無風(fēng)險(xiǎn)資產(chǎn)的風(fēng)險(xiǎn)溢價(jià)情況，形成波動報(bào)酬(Reward to Variability)，即組合預(yù)期收益與無風(fēng)險(xiǎn)報(bào)酬率之間的差值與標(biāo)準(zhǔn)差的比值，從而更好地把握風(fēng)險(xiǎn)與收益情況，完成本研究證券投資組合中資本資產(chǎn)配置的簡單數(shù)學(xué)特征分析。整理得到如表2所示的權(quán)重調(diào)節(jié)變量情況。

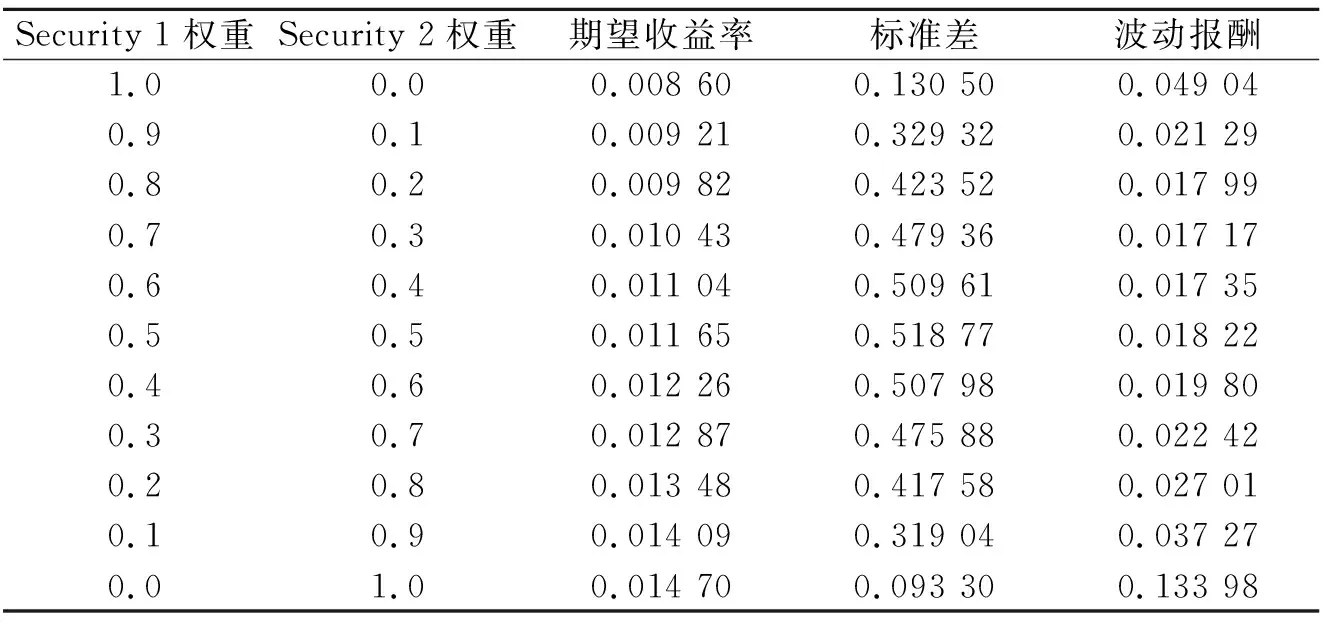
表2 權(quán)重調(diào)節(jié)變量情況Tab.2 Weight adjustment variables

調(diào)整變量值，引起其他變量發(fā)生改變，通過兩個(gè)風(fēng)險(xiǎn)模型的資產(chǎn)配置分析，選擇兩個(gè)風(fēng)險(xiǎn)證券Security 1與Security 2同國債Bond之間的期望值、標(biāo)準(zhǔn)差以及相關(guān)系數(shù)的改變，構(gòu)建不同權(quán)重的最優(yōu)市場組合，以CAPM資本資產(chǎn)定價(jià)模型的計(jì)算公式，得出組合預(yù)期收益率、標(biāo)準(zhǔn)差以及報(bào)酬波動的比率，即資本配置線的斜率。根據(jù)自我設(shè)定的參數(shù)進(jìn)行多次的數(shù)值調(diào)試，不同風(fēng)險(xiǎn)偏好的投資者對于風(fēng)險(xiǎn)資產(chǎn)預(yù)期回報(bào)率的不同以及各個(gè)資產(chǎn)的配置權(quán)重差異，可進(jìn)行合理定制化投資方案選擇。

在不允許賣空的交易機(jī)制下，分析最小方差組合以及最優(yōu)風(fēng)險(xiǎn)組合的資產(chǎn)配置情況，結(jié)合上述的實(shí)證研究數(shù)據(jù)，筆者整理得到如表3所示的風(fēng)險(xiǎn)差異資產(chǎn)配置情況。

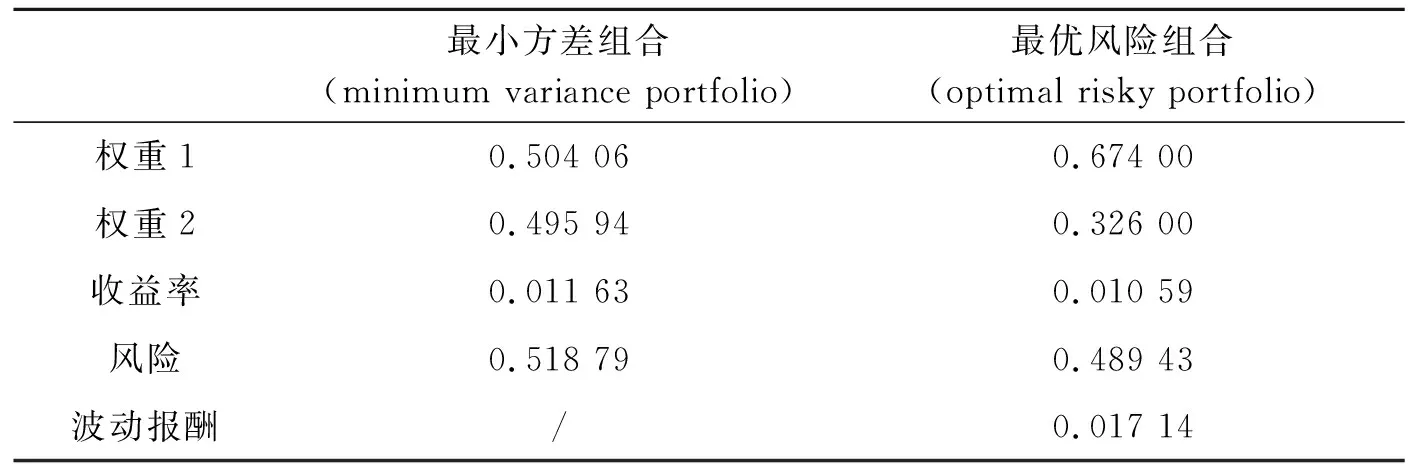
表3 風(fēng)險(xiǎn)差異資產(chǎn)配置情況Tab.3 Risk difference asset allocation

在證券投資組合的可行集區(qū)域中，其內(nèi)部與邊界范圍所形成的投資組合，完全可以根據(jù)投資者不同的偏好程度形成獨(dú)特的投資決策。對于最廣大的理性投資者來說，在同一風(fēng)險(xiǎn)水平下，投資者都會選擇收益率最高的投資組合；而對于同一收益水平下，投資者都會選擇風(fēng)險(xiǎn)最小的投資組合。據(jù)此，將能夠同時(shí)滿足預(yù)期收益最大且組合風(fēng)險(xiǎn)最小的投資組合，構(gòu)成最有效的配置集合。

2.3 分析結(jié)論

在現(xiàn)行證券市場上進(jìn)行資本資產(chǎn)配置組合的實(shí)際案例分析，以風(fēng)險(xiǎn)資產(chǎn)的股票證券形式和無風(fēng)險(xiǎn)資產(chǎn)的國債構(gòu)建投資組合。采用一般化的數(shù)字特征的分析，進(jìn)行收益率和標(biāo)準(zhǔn)差的數(shù)字化處理，進(jìn)行最小方差組合和最優(yōu)風(fēng)險(xiǎn)組合的兩者均衡條件下，探索證券投資組合收益和方差之間的協(xié)調(diào)關(guān)系。筆者參考Investments[11]提供的數(shù)據(jù)，整理得到資產(chǎn)配置模型結(jié)果示意圖(圖1)。

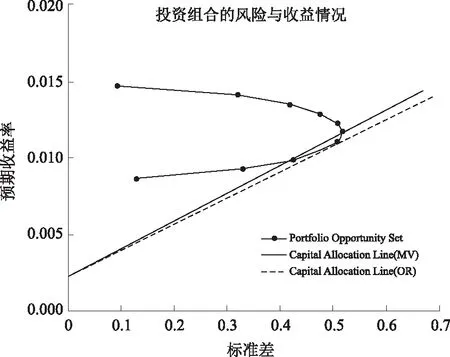
圖1 資產(chǎn)配置模型結(jié)果示意圖Fig.1 Schematic diagram of asset allocation model results

如圖1所示，實(shí)證數(shù)據(jù)表明，在構(gòu)建的三一重工、貴州茅臺和中國一年期國債收益率的投資組合之中，能夠在組合標(biāo)準(zhǔn)差0.4～0.6的區(qū)間內(nèi)，實(shí)現(xiàn)最優(yōu)化預(yù)期收益的資產(chǎn)配置。但是本次分析不足之處，是僅停留在理論收益與風(fēng)險(xiǎn)情況，現(xiàn)有市場不一定能找到合理的資產(chǎn)組合，且資產(chǎn)間的相關(guān)系數(shù)不能根據(jù)統(tǒng)一標(biāo)準(zhǔn)得出，選取的大盤股票指數(shù)仍缺乏客觀性。

在不允許賣空的市場環(huán)境條件下，選擇最小方差投資組合即風(fēng)險(xiǎn)最小化組合：進(jìn)行最優(yōu)風(fēng)險(xiǎn)資產(chǎn)投資組合的權(quán)重配比以及無風(fēng)險(xiǎn)資產(chǎn)的選擇，實(shí)現(xiàn)最近點(diǎn)連線，即構(gòu)建最小方差組合，實(shí)現(xiàn)最低風(fēng)險(xiǎn)保障。選擇最優(yōu)投資組合：通過調(diào)節(jié)兩個(gè)風(fēng)險(xiǎn)資產(chǎn)的不同權(quán)重實(shí)現(xiàn)與無風(fēng)險(xiǎn)資產(chǎn)之間的連線，在所形成的可選擇權(quán)重范圍內(nèi)進(jìn)行投資方案的制訂，根據(jù)所期望的回報(bào)率調(diào)整已選定的投資組合權(quán)重和無風(fēng)險(xiǎn)資產(chǎn)之間的配比，達(dá)到既定的收益情況。也可以通過調(diào)節(jié)兩個(gè)風(fēng)險(xiǎn)資產(chǎn)的權(quán)重，間接地影響投資組合的整體收益率，從而實(shí)現(xiàn)預(yù)期回報(bào)。組合模型的規(guī)劃求解，需要在結(jié)合眾多市場信息后，進(jìn)行擬合優(yōu)度最大化的數(shù)字模擬。

3 結(jié)論

通過對風(fēng)險(xiǎn)投資模型進(jìn)行數(shù)理統(tǒng)計(jì)分析，將證券投資組合理論以更加直觀簡潔的形式描述，得出風(fēng)險(xiǎn)投資的風(fēng)險(xiǎn)與收益情況，以量化思維分析證券市場上的理性和非理性行為，為投資決策者作出合理的判斷與選擇，更加理性和辯證地看待收益和風(fēng)險(xiǎn)之間的關(guān)系。實(shí)證研究從離散化的隨機(jī)變量入手，轉(zhuǎn)化為收益情況的連續(xù)型變量，對期望值、方差、相關(guān)系數(shù)以及協(xié)方差的基本數(shù)字特征進(jìn)行分析。在下一步的數(shù)學(xué)特征分析中，可以加入變量的獨(dú)立性因素進(jìn)行更加符合實(shí)際的研究，也能夠深入地完善和提升投資組合模型的擬合程度，為投資決策提供更為便捷的數(shù)理支撐，為風(fēng)險(xiǎn)資產(chǎn)投資組合理論的數(shù)學(xué)特征應(yīng)用融入更多的實(shí)用性優(yōu)勢。