基于改進遺傳算法的電液伺服系統軌跡控制

宋倩玉， 馮 浩， 劉慧勤， 周世萱， 朱雅利， 張亦心， 殷晨波,3

(1.南京信息工程大學 人工智能學院， 江蘇 南京 210044；2.南京工業大學 挖掘機關鍵技術聯合研究所， 江蘇 南京 211816； 3.三一重機有限公司， 江蘇 昆山 215300)

引言

提高智能化控制水平是挖掘機器人發展的重要趨勢，而運動軌跡控制是實現智能化的基礎和關鍵。在自動控制技術、互聯網技術、智能算法等眾多前沿成果的推動下，學者們在挖掘機器人軌跡控制方面做了很多研究[1]。鄒樹梁等[2]采用模糊位置控制的方法提高了單個鏟斗電液伺服系統的軌跡跟蹤精度。PARK J等[3]提出了一種適用于挖掘機器人的回聲狀態網絡控制策略。此外學者們還嘗試了將諸如神經網絡[4]、滑模控制[5]、自適應控制[6]等智能算法運用在挖掘機器人軌跡控制中。

現代工業控制中，新型控制策略層出不窮，但是經典的PID控制器因具備結構簡單、實現容易、魯棒性強等優點，仍然處于工業控制的主導地位。PID控制器的參數與系統性能直接相關，但是傳統PID參數調試方法耗時耗力。將粒子群算法、專家系統、神經網絡、蟻群算法等算法應用于PID控制器中，解決傳統PID的局限性，滿足各種控制要求，已經成為PID的重要研究方向。

遺傳算法(Genetic Algorithm，GA)是基于達爾文進化論中自然界進化過程來求解問題的方法，通過對種群的選擇、交叉和變異等遺傳操作，不斷獲得更優的群體，重復此過程，直到滿足已設定的收斂指標。由于其思想簡單、易于實現并且具有很強的全局優化搜索能力，GA已經廣泛應用于參數優化[7]、故障診斷[8]、參數辨識[9]等。運用GA優化PID參數，不需要復雜的規則就可以尋求全局最優解，在自動控制和機器人等領域GA已經得到了廣泛應用。BATAYNEH W等[10]使用GA算法得到最優的PID參數，實現移動機器人的高精度軌跡跟蹤。ZAHIR A等[11]為了提高電機的性能，采用GA對PID參數進行優化。

但是，標準遺傳算法(Standard Genetic Algorithm，SGA)具有早熟收斂和停滯在全局最優解的缺點。為了克服此缺點， 許多學者提出了各種改進策略。POAP D[12]提出了一種自適應遺傳算法來保持種群的多樣性。CHAI Z等[13]提出了一種自組織的遺傳算法，其具有良好的全局搜索性能和收斂速度。

本研究針對挖掘機器人電液伺服系統的軌跡控制要求，提出一種改進遺傳算法(Improved Genetic Algorithm，IGA)優化的PID控制器，對遺傳算法的種群、適應度函數、交叉概率和變異概率均進行了改進，以提高挖掘機器人伺服系統的軌跡控制精度。

1 挖掘機器人系統模型

1.1 系統概述

為實現挖掘機器人的自動控制，首先需要將原有的液控操作方式改造為電控；為獲取液壓缸位移，在挖掘機器人液壓缸上安裝位移傳感器；為獲取壓力，在液壓缸油口安裝壓力傳感器。以實驗室23 t級的挖掘機器人為研究平臺，將其原有的手動先導控制改造為電控，可以直接利用計算機進行運動控制，改造后的挖掘機器人系統原理圖如圖1所示，主要包括先導閥、多路閥、液壓缸、控制器、拉線式位移傳感器等。

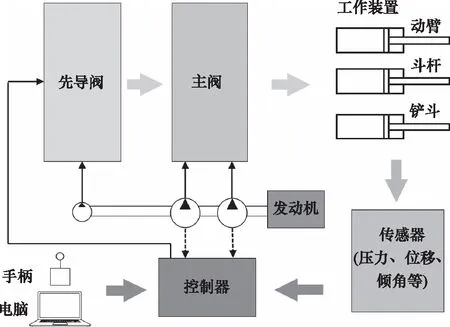
圖1 挖掘機器人簡圖Fig.1 Schematic diagram of robotic excavator

1.2 電液伺服系統數學模型

挖掘機器人電液伺服系統框圖如圖2所示，主要包括控制器、放大器、比例減壓閥、多路閥、液壓缸和反饋機構，建立如下簡化模型。

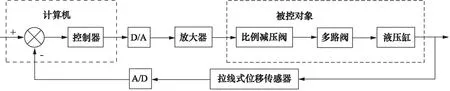
圖2 挖掘機器人電液伺服系統框圖Fig.2 Electro-hydraulic proportional control system

1) 放大器環節

控制器產生的電壓信號經過放大器后將變成電流信號，并輸出到先導閥，可以當做比例環節，傳遞函數為：

(1)

式中，Ka—— 放大增益

I(s) —— 電流信號

U(s) —— 電壓信號

2) 電液比例環節

電液比例環節包括先導閥和多路閥，忽略次要因素建立模型，將其視為一階環節：

(2)

式中，Kb—— 電流增益

xv(s) —— 多路閥閥芯位移

T—— 時間常數

3) 閥控非對稱液壓缸環節

閥控非對稱液壓缸環節主要包括3個方程，分別是負載流量方程、液壓缸流量方程及力平衡方程。為便于分析，假設油源壓力穩定，回油壓力為0，針對液壓缸伸出工況，油液經過多路閥的線性化負載流量方程為：

QL=Kqxv-KppL

(3)

式中，Kq—— 流量增益

Kp—— 壓力系數

pL—— 負載壓力

液壓缸流量方程為：

(4)

式中，A1—— 無桿腔有效面積

y—— 位移

V—— 液壓缸總體積

βe—— 油液彈性模量

Ct—— 泄漏系數

忽略油液的摩擦力和質量，液壓缸力平衡方程為：

(5)

式中，A2—— 有桿腔有效面積

m—— 負載等效質量

Bc—— 黏性阻尼系數

K—— 負載彈簧剛度

FL—— 等效負載力

將上述的3個方程進行拉式變換和簡化，得到伸出工況下閥控非對稱液壓缸的數學模型：

(6)

(7)

式中，wh—— 液壓固有頻率

ξh—— 阻尼比

Kt—— 總流量壓力系數

液壓缸收縮過程的數學推導與上述過程類似，區別在于參數大小不同。

4) 反饋環節

反饋環節采用拉線式位移傳感器，其傳遞函數為：

(8)

式中，Uc(s) —— 反饋電壓

Kd—— 反饋增益

2 控制器設計

2.1 PID控制

為提高挖掘運動軌跡的精度，降低勞動強度，將經典PID控制引入到控制系統中。PID控制是根據偏差e(t)=y(t)-r(t)進行控制，r(t)為系統輸入，y(t)為系統輸出，將e(t)的3種不同的運算，即比例、積分和微分構成控制量u(t)，其參數整定后基本保持不變，控制規律為:

(9)

式中，KP—— 比例增益，主要調節系統的精度

KI—— 積分增益，主要消除系統的穩態誤差

KD—— 微分增益，主要改善系統的動態特性

經典PID控制器參數整定過程較長，常用的整定方法有Ziegler-Nichols法(Z-N)、繼電特性法等，這些方法難以獲得最優的控制參數，并且在挖掘機器人工作工況變化較大時，系統的總體控制精度會變差。

2.2 SGA控制

SGA數學模型為：

SGA=(C,F,P0,M,Φ,μ,θ,Tc)

(10)

式中，P0—— 初始化種群

Tc—— 終止條件

C—— 編碼方式

F—— 適應度函數

M—— 群體大小

Φ，μ，θ—— 選擇、交叉和變異算子

SGA將問題看作群體中的個體或染色體并對其編碼，模擬達爾文的自然界中的遺傳和淘汰機制生物進化中的繁殖、交叉以及基因突變現象，根據適應度函數對后代評估，不斷迭代優化過程，直到滿足收斂條件，算法流程如圖3所示。

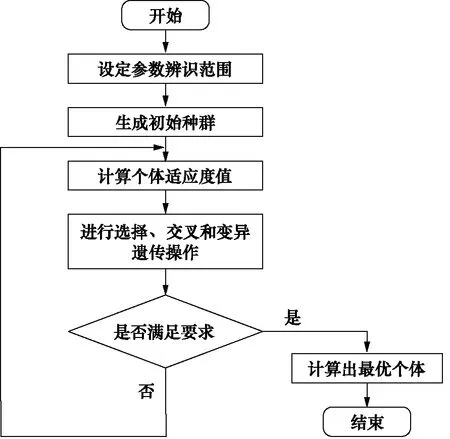
圖3 SGA流程Fig.3 Flowchart of SGA

SGA需要確定的主要運行參數有：群體大小M一般取[10,200]，終止迭代次數G一般取[100,500]，交叉概率Pc一般取[0.49,0.99]，變異概率Pm一般取[0.001,0.1]，這些參數對算法的影響較大。群體大小與求解問題的非線性相關，交叉提高搜索速度，變異增加多樣性。合理配置交叉和變異可以使搜索能力得到提高。

2.3 IGA控制

SGA的交叉概率和變異概率在算法中是不變的，因此，SGA存在早熟的缺陷，且SGA的初始種群為隨機生成，運行效率不高，對SGA做如下改進。

1) 種群改進

針對SGA中隨機生成初始種群會影響運行效率的情況，利用Z-N階躍響應法得到具體的參數值，在參數值附近給定參數的取值范圍，在取值范圍內進行參數的優化，減少運算量。

2) 適應度尺度變換

在算法的不同階段，對適應度進行變換。采用適應度比例選擇法，設個體的適應度值為Fi，則該個體被選中的概率Pi為:

(11)

通過縮放個體適應值實現適應度尺度變換，將適應度值較大的個體進行適當的縮小，降低其被遺傳的概率，對適應度值較小的個體進行適當的放大，增加其被遺傳的概率。采用線性尺度變換方法變換適應度，增加物種的多樣性，變換公式為:

(12)

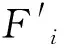
(13)

式中，Fmin和Favg分別為個體原適應度的最小值和平均值。

3) 交叉概率Pc和變異概率Pm的調整

在不同的迭代時期，調整Pc和Pm的值。種群趨于收斂時，為了防止算法早熟，需要增大Pm，減小Pc；種群發散時，為了使算法盡快收斂，需要增大Pc，減小Pm。同時，為了較優的個體不變化，避免局部最優解，需要將具備最大適應度值的個體的Pc和Pm分別提高到Pc1和Pm1。

兩者的調整公式為:

(14)

(15)

式中，k1～k4區間為(0,1)，Fmax為個體適應度最大值，F′和F為待交叉2個個體中比較大的適應度值和待變異的個體適應度值，Pc1=0.9，Pm1=0.1，Pc2=0.6，Pm2=0.001。

在算法優化控制器的參數時，為使控制系統快速而又平穩，同時避免控制量突變，引入輸入平方項，采用式(16)為目標函數J:

(16)

式中，tu為系統上升時間，w1～w3為權值。引入超調量，當e(t)<0時，目標函數J為:

(17)

式中，w4為權值且w4>>w1。

目標函數J和適應度函數F的轉化關系為F=1/J。

IGA可自動尋找一組最佳的PID非線性組合參數，對控制系統的PID參數優化的步驟如下：

(1) 利用Z-N階躍響應法得到具體的參數值，在參數值附近給定參數的取值范圍并進行編碼；

(2) 產生M個個體組成的初始總群P0；

(3) 對個體解碼，求出適應度值；

(4) 進行適應度尺度的變換縮放；

(5) 求出交叉概率Pc和變異概率Pm的值對種群Pt進行操作，產生下一代種群Pt+1；

(6) 重復步驟(4)和步驟(5)，直至參數達到預定的目標。

3 仿真分析

在MATLAB中建立不同的PID控制器，在AMESim中建立挖掘機器人鏟斗伺服系統，聯合控制器和伺服系統搭建仿真平臺，如圖4所示。通過階躍和斜坡這2個最具有代表性的挖掘軌跡，將IGA，SGA和傳統的Z-N PID控制器的性能進行比較，控制器參數如表1所示。

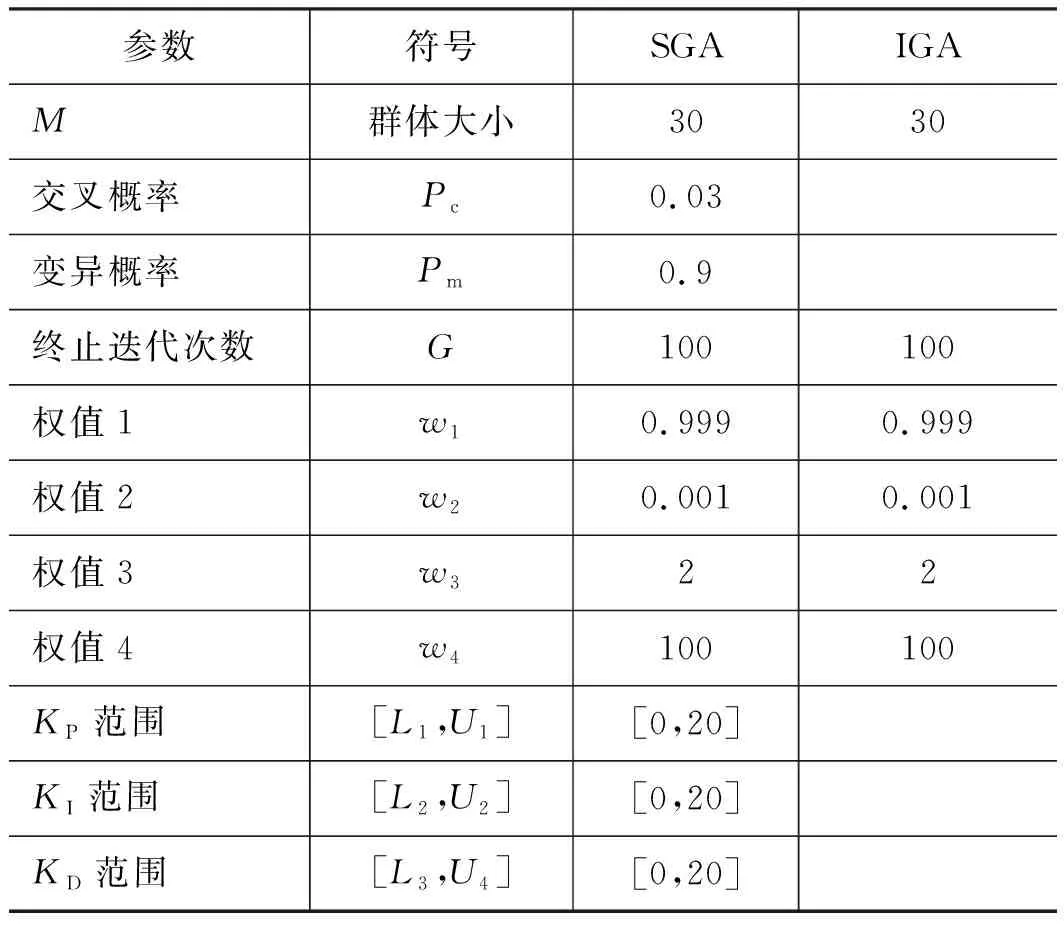
表1 控制器主要參數Tab.1 Main parameters of controller

圖5為采用階躍信號時，不同控制器得到的響應曲線。可以看出，SGA控制器和IGA控制器有良好的跟蹤性能，均優于傳統的Z-N控制器。其中，Z-N 控制器的上升時間、穩定時間分別為1.75 s和2.83 s，為3種控制方法中最大。從穩定時間來比較，IGA控制器的穩定時間為1.81 s，最快達到穩定。IGA控制器超調量小，系統調整時間短，響應更加快速。

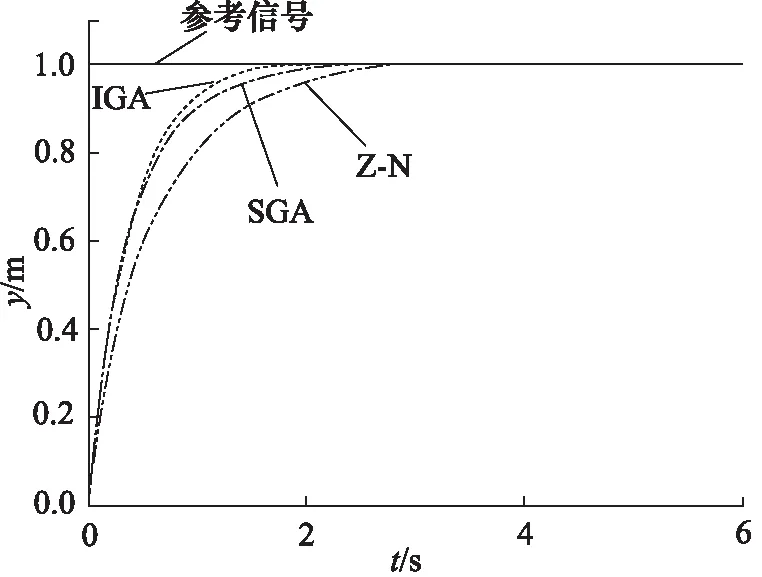
圖5 階躍輸入位移響應曲線對比Fig.5 Comparison of position responses with step reference input

圖6中，IGA控制器的收斂速度明顯快于SGA控制器。IGA控制器和SGA控制器的最佳目標函數Jbest分別為24.56和 24.82。IGA控制器在48次迭代后收斂，而SGA控制器需要迭代69次。

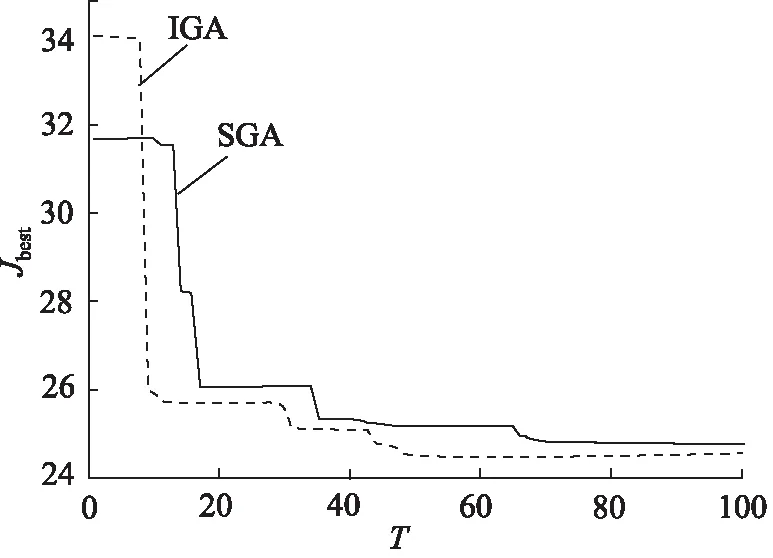
圖6 IGA和SGA的收斂曲線Fig.6 Comparison of convergence curves of IGA and SGA

采用斜率為0.25的斜坡信號作為第2種參考軌跡，3個控制器的響應曲線和跟蹤誤差如圖7、 圖8所示。IGA控制器的響應速度最快，精度最高，響應延遲為0.07 s，SGA和Z-N控制器的響應延遲分別為0.19 s 和0.63 s。對于鏟斗液壓缸，其最大行程為1156 mm，因此超過工作行程時，跟蹤曲線為直線。IGA控制器在4.69 s時達到最大行程，Z-N控制器為5.25 s。IGA控制器最大跟蹤誤差僅為24.23 mm，SGA和Z-N控制器分別為46.99 mm和156.62 mm。

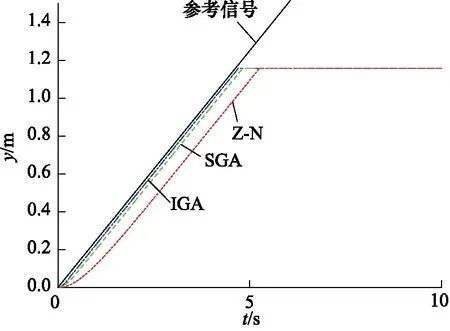
圖7 斜坡輸入位移響應曲線對比Fig.7 Comparison of position responses with slope reference input

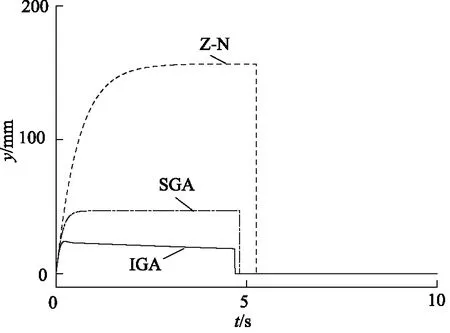
圖8 斜坡輸入軌跡誤差對比Fig.8 Comparison of position errors with slope reference input

4 軌跡控制實驗

為了實際驗證IGA控制器在挖掘機器人軌跡控制中的應用，在實驗室23 t挖掘機器人上搭建了如圖9所示的軌跡控制實驗平臺。

1.壓力傳感器 2.電子羅盤 3.拉線式位移傳感器 4.主閥5.DSP控制器 6.軌跡控制系統 7.23 t挖掘機器人圖9 挖掘機器人軌跡控制實驗平臺Fig.9 Trajectory control experiment platform

軌跡控制實驗方案為控制鏟斗齒尖進行斜線運動，即挖斜坡作業，先將鏟斗齒尖調整到起點位置，然后跟蹤斜坡軌跡，直至斜坡終點。圖10、圖11分別為斜坡作業時的鏟斗齒尖運動軌跡及誤差。

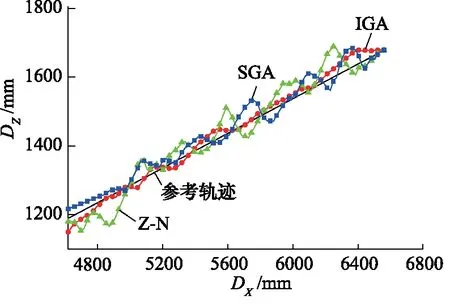
圖10 斜坡作業時的鏟斗齒尖運動軌跡Fig.10 Bucket tip tracks under slope line condition

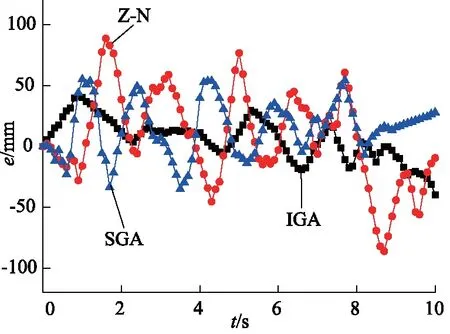
圖11 斜坡作業時的鏟斗齒尖軌跡誤差Fig.11 Bucket tip tracking errors under slope line condition

從控制效果看，3種PID方法均能產生一定的控制效果。IGA控制器對軌跡的跟蹤更接近預定軌跡，從誤差曲線可以得出，IGA控制器比SGA控制器的控制精度高。Z-N控制器的最大誤差為86.13 mm，而SGA控制器和IGA控制器的最大誤差分別為54.21 mm和41.21 mm。此外，還研究了每個軌跡的均方根誤差，SGA控制器為26.49 mm，IGA控制器為17.74 mm。很顯然，IGA控制器的誤差是在3個控制器中最小的，IGA控制器的跟蹤性能比SGA控制器提高了約33.03%。

5 結論

針對挖掘機器人電液伺服系統的高精度軌跡的控制要求，對遺傳算法的種群、適應度函數、交叉概率和變異概率進行了改進，設計了IGA的PID控制器。輸入不同信號對控制系統進行仿真分析，驗證了IGA控制器調整時間短，響應快速。采用挖斜坡作業驗證了優越性，IGA控制器的跟蹤誤差比SGA控制器減少了33.03%。但是，控制器中的某些參數沒有具體的規則，有待于后續深入研究。