基于改進麻雀算法的卷繞張力控制系統

譚龍彪，肖金鳳

(南華大學 電氣工程學院，湖南 衡陽 421200)

設備中的收卷、放卷系統對設備的運行速度和產品質量有較大的影響。卷繞速度快，控制不容易穩定，產品質量差；卷繞速度慢，雖然產品質量得到了保障，但生產效益不高。因此一個穩定的張力控制系統對保障產品質量和提高運行速度至關重要。

現有的卷繞控制系統大多運用PID控制理論。即使PID控制理論運用得十分成熟了，但還是有局限性，而韓京清在針對PID的控制誤差的計算、誤差的提取、PID加權和和積分反饋的副作用4個方面提出了更好的控制策略，即安排過渡過程、合理提取微分和跟蹤(TD)、非線性組合(NF)和擾動估計的擴張狀態觀測器(expansion state observer，ESO)，并提出了新型控制器自抗擾控制器[1]。自抗擾控制器(active disturbance rejection control，ADRC)不僅保留PID控制理論，而且還對控制對象的模型精確性要求很低，也就是既可以是未知的模型，也可以是完全了解的模型。

麻雀算法(SSA)是今年來新提出的群智能算法。SSA是通過模擬麻雀種群覓食過程中的行為進行迭代計算獲取最優解。雖然麻雀算法具有迭代計算過程簡單、調節參數少和收斂速度快等優點[2]，但也具有群智能算法的易陷入局部最優的通病。通過對SSA進行仿真可以發現：其容易收斂到原點；其次，SSA的位置更新是以跳躍的方式向當前最優靠近，容易忽略某些較優的解。針對SSA的這2個缺點，提出引入粒子群算法(PSO)的速度更新算子。PSO中粒子是以參考當前最優位置和個體最優位置實時修改粒子的速度進行尋優[3]，并對SSA的發現者和跟隨者位置更新公式進行修改，改進SSA對最優解的收斂性和尋優過程，減弱對原點的收斂。為保持麻雀種群的多樣性，在更新警戒者位置后，再對麻雀個體進行遺傳算法(GA)的交叉、變異操作，GA中的基因交叉、變異計算符合遺傳規律,可為種群的基因庫保持多樣性[4]。

SSA算法適用于多目標優化，如機器人路徑規劃、圖像處理和組合優化等問題[5]，目前還沒有用于ADRC參數的整定方面，且ADRC需整定的參數有6個。綜上，課題組將改進的麻雀算法(PGSSA)用來整定ADRC控制器的參數，建立了一個以ADRC作為控制器的張力控制系統。

1 張力控制系統模型

為了研究復卷機的張力控制系統，選擇其收卷過程作為研究對象。

1.1 收卷過程問題描述

收卷過程容易受到各種因素的影響，如放卷過程線速度、牽引輥的線速度、卷徑及外部擾動等。產品的質量取決于收卷過程張力的穩定控制。運行中，若張力過小，卷軸上的材料不易卷緊，材料會出現褶皺；若張力過大，會使材料外層擠壓內層易造成變形，甚至會發生材料斷裂。通過研究和計算，發現收卷過程中卷材上的張力主要是受到線速度和卷徑的影響，即保持穩定的線速度運行條件下，通過卷徑的變化可以控制張力[6]。也就是根據卷徑的變化改變驅動電機輸出轉矩來控制張力：

Fzl=Meo/r0。

(1)

式中：Meo為收卷軸的扭矩，r0為收卷軸的卷徑。

1.2 收卷張力控制系統的傳遞函數

整機中采用變頻器控制電機的輸出轉矩，而張力控制系統中需要控制的設備為變頻器和收卷電機。因為ADRC控制器對于控制對象模型的要求不高，為了簡化計算，將變頻器和收卷電機都設定為慣性環節[7]。收卷電機為型號YVF2-112M-4的三相異步變頻調速電動機，額定功率為4 kW，額定電壓為380 V，額定電流8.8 A，額定頻率50 Hz,額定轉矩25.4 N·m，其傳遞函數簡化為：

(2)

式中：Km為電動機傳遞函數的前向增益，Tm為電動機傳遞函數的慣性時間常數。

選用型號為HD50-T的變頻器,其傳遞函數Gb與Gd一樣，只是參數有差別，通過查手冊可計算得控制系統中被控對象的傳遞函數為：

(3)

2 改進麻雀算法

2.1 麻雀算法

由薛建凱和沈波于2020年提出的麻雀算法是一種新型的群智能算法。通過模擬麻雀群體中個體覓食和群體覓食還有在覓食過程對危險預警的運動規律，建立數學模型進行迭代尋優的新型群智能優化算法[8]。經過眾多學者對其進行仿真和多方面測試，麻雀算法具有一些特點：參數就只有Q，β，K，且都是隨機數，不需要進行繁瑣的參數調整；收斂速度快，在求解原點附近的解時迭代尋優的性能很高，若是最優解不在原點附近其性能就會下降；算法步驟清楚簡潔，公式簡單易于實現；麻雀群體多樣性差，容易陷入局部最優解；在收斂過程中，個體解是直接跳躍到目前最優解附近的移動方式，也就會產生“早熟”，尋找的最優解很可能就是局部最優，這說明麻雀算法的全局搜索能力比較弱。

麻雀算法通過麻雀覓食時不同的行為特征，將麻雀群體分為發現者(占群體的10%～20%)和跟隨者(群體剩下的麻雀)，發現者具有較好的適應值，負責搜索食物豐富且安全的區域，跟隨者通過監控發現者的行為，跟隨發現者覓食，且兩者之間的身份不是固定的，取決于適應值。除此之外還有預警者(隨機出現，占群體的10%～20%)，這是在發現者和跟隨者中發現危險并發出預警的麻雀。

2.2 改進麻雀算法

針對麻雀算法的以跳躍的方式移動而陷入局部收斂和原點收斂性強的特點，通過引入粒子群算法的速度算子(式(4))，代替原麻雀算法公式中的exp()部分，改變麻雀的跳躍移動方式向當前最優解收斂，使得每只麻雀以速度v向當前最優解移動，增強麻雀算法向最優解的搜索能力和全局搜索能力。

vi(t+1)=ωvi(t)+C2r2[Xgbest-Xi(t)]。

(4)

式中：Xgbest為全局最佳位置，vi(t)為第i只麻雀第t次迭代時的速度，Xi(t)為第i只麻雀第t次迭代時的位置,ω為慣性系數影響搜索能力，且ω采用范圍為[0.8,1.2]的錐度控制；C2為大于零的學習因子，用于調節自身位置的步長；r2是[0,1]之間的隨機數。

改進后發現者位置更新為：

(5)

式中：Q為正態分布的隨機數，R2為隨機數。

當警戒值R2小于警戒閾值St時，發現者會帶著跟隨者在附近范圍為內尋找最優值；當大于時，說明有危險，發現者會離開這個地方尋找安全的區域覓食。

改進后跟隨者位置更新為：

(6)

適應值較好的跟隨者，說明離發現者位置近更容易獲取食物；而適應值較差的跟隨者，會因為距離遠搶不到食物，就得嘗試換個區域覓食。

改進后警戒者位置更新為：

(7)

式中β是服從均值為0，方差為1的正態分布隨機數。

采用式(7)，改變麻雀預警到危險時會以β步長在全維度上向當前最優位置移動。

而針對麻雀算法多樣性差的問題，可以選擇引入遺傳算法中的交叉算子和變異算子。就如群體中偶爾會出現不安分的麻雀，會不按照常規改變自身當前的位置，從而增加算法的個體多樣性。

2.3 適應度函數

收卷張力控制系統具有快速性、穩定性、準確性且抗擾能力強的特點。結合性能指標，如上升時間、峰值時間、最大超調量和調節時間等，選擇時間乘絕對誤差的誤差積分準則ITAE作為目標函數[9]；考慮到控制量可能會過大，且為了避免超調量，也將超調量作為ITAE中的一項：

(8)

當ey(t)<0時，

(9)

式中：w1,w2,w3,w4為權值且w4?w1，取值為w1=0.999,w2=0.001,w3=2.000,w4=100.000；e(t)為誤差;u(t)為控制量;ts為上升時間;ey(t)=y(t)-y(t-1)；y(t)為被控對象輸出。

將基于上述改進方法的麻雀算法應用到改進自抗擾控制器參數優化中，具體步驟為：

1)初始化麻雀種群，設定好種群數量、迭代次數、麻雀類型比例和搜索空間維度等參數，并且初始化每個麻雀的位置和速度。

2)將每個麻雀的位置作為ADRC的參數進行控制，根據ITAE計算適應值。

3)根據適應值大小對麻雀進行排序。

4)更新麻雀個體的速度。

5)根據適應值重新選擇發現者和跟隨者，并更新位置。

6)隨機產生數名警戒者，并更新位置。

7)對所有麻雀個體進行交叉、變異操作。

8)判斷是否達到迭代次數，若沒到，則從步驟2)重復計算；若達到則結束計算，并且輸出最佳適應值和最優ADRC控制參數。

改進SSA算法步驟如圖1所示。

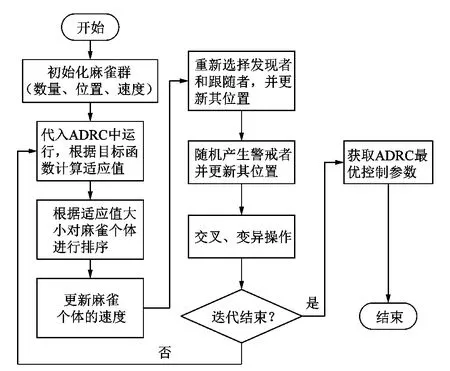
圖1 改進SSA算法步驟

3 自抗擾控制器

基于韓京清解決控制問題的新思路——在系統運行過程中施加控制力來達到控制目的的過程控制[10-11]，以及在PID控制技術的基礎上結合現代優秀控制技術，再經過仿真提出了自抗擾控制技術。該技術的核心控制原理是將系統的未建模動態和未知擾動都歸結為對系統的總擾動而進行估計并補償。自抗擾控制技術主要由3個子技術組成的：跟蹤微分器(TD)、擴展狀態觀測器(ESO)、非線性反饋效應(NLSEF)，ADRC結構圖如圖2所示。

自抗擾控制器的控制過程為：

1)安排過渡過程，將輸入信號v通過跟蹤微分器過渡為跟蹤信號x1，同時輸出對應的微分信號x2。

2)建立過擴張狀態觀測器，將被控對象的輸入信號u和輸出信號y，計算得到被控對象的狀態信號z1，z2和被控對象受到的總擾動z3。

3)計算出系統的狀態誤差e1=x1-z1，e2=x2-z2，并且根據狀態誤差e1，e2確定非線性反饋效應中的誤差反饋律。

4)用系統受到的總擾動值z3對誤差反饋控制量u0進行補償，以此來確定控制被控對象的控制量u為：

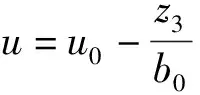
(10)

3.1 跟蹤微分器

本研究中的過渡過程采用離散形式非線性的跟蹤微分器，離散形式可以避免進入穩態時產生的高頻振蕩[11]，TD的形式為：

(11)

式中：v為輸入信號，x1和x2分別為對應的輸入跟蹤信號和微分信號，h為積分步長，r為速度因子(決定跟蹤速度)，h0為濾波因子(對噪聲濾波)，函數fhan()為離散系統的最速控制綜合函數。

3.2 擴張狀態觀測器

狀態觀測器是利用被控對象的輸入信號和輸出信號來確定其狀態的裝置;而擴張狀態觀測器其實就是在狀態觀測器的基礎上擴張新的狀態觀測量。自抗擾控制器中擴張狀態觀測器擴張的狀態變量是被控對象受到的總擾動，也就使得ADRC能夠實時估計系統擾動[12]，并且對該擾動進行補償。ESO在離散系統中的形式為：

(12)

式中：b0為補償系數;β01,β02,β03是可調參數，決定了ESO對狀態的估計能力；一般情況下取α1=1,α2=0.5,α3=0.25;參數δ1根據實際情況選取。

3.3 非線性狀態誤差反饋律

非線性狀態誤差反饋律是將經典PID控制技術中P，I和D三者的加權和改成非線性組合，也就是非線性PID的控制方法，其在離散系統中的形式為：

(13)

式中：β1,β2為可調參數，是比例和微分增益，對控制量有著關鍵作用，一般情況下取α4=0.75,α5=1.25;參數δ2與控制精度有關。

綜上所述，即便自抗擾控制器的表達式中有著很多參數，但實際上需要進行最優化整定的參數為{β01,β02,β03,β1,β2,b0}，其他的相關參數可以根據實際經驗確定為恒定值。控制系統結構如圖3所示。

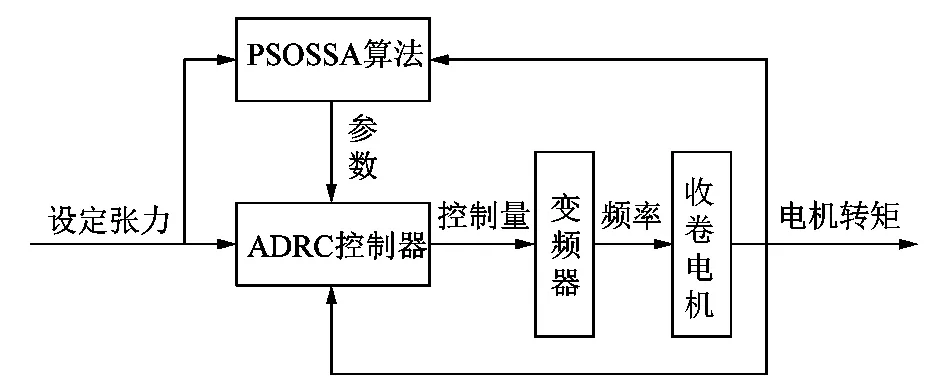
圖3 基于PSOSSA的ADRC系統框圖

4 實驗仿真分析

結合上述的分析和理論，采用MATLAB和Simulink軟件平臺，對收卷張力控制系統整定ADRC控制器的參數進行仿真。采樣時間設定為tc=10 ms，將系統設定的階躍信號作為輸入信號。PSOSSA和SSA算法仿真對比，麻雀群的大小為30；迭代次數為1 000，變量數(空間維度)為6，預警值為0.8；發現者比例為0.2；預警者比列為0.2；ADRC整定參數為{β01,β02,β03,β1,β2,β0}，其最小值的設定為{0,0,0,0,0,0}，其最大值的設定為{50,200,1 000，50,50,10}；ADRC控制器的速度因子r為300，濾波因子h為0.2。

4.1 無擾動仿真

在不存在擾動影響的條件下，對2種算法分別進行同樣次數的仿真，如表1所示。

表1 仿真優化整定的ADRC參數

2種算法的適應度函數計算的最優適應值如圖4所示。

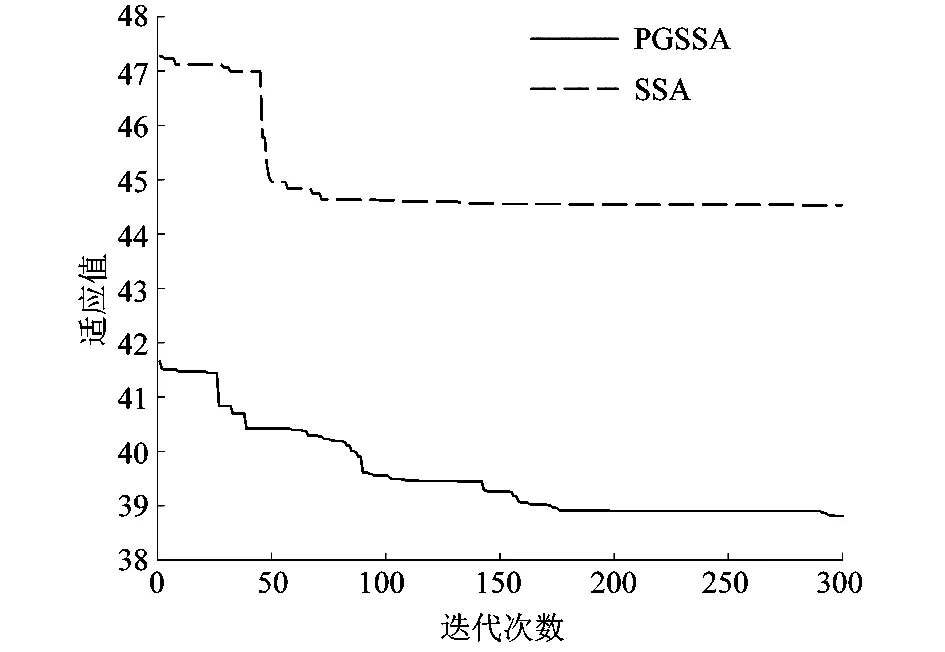
圖4 最優適應值

ADRC控制系統應用2種算法整定后參數的無擾動階躍響應曲線如圖5所示。

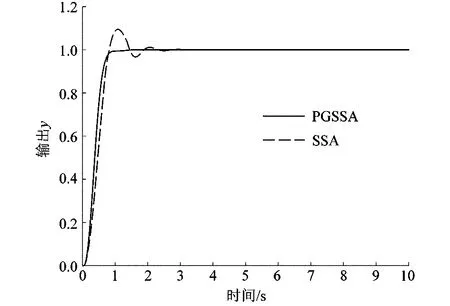
圖5 無擾動階躍曲線

根據階躍響應的性能指標進行分析，兩者的數據如表2所示。

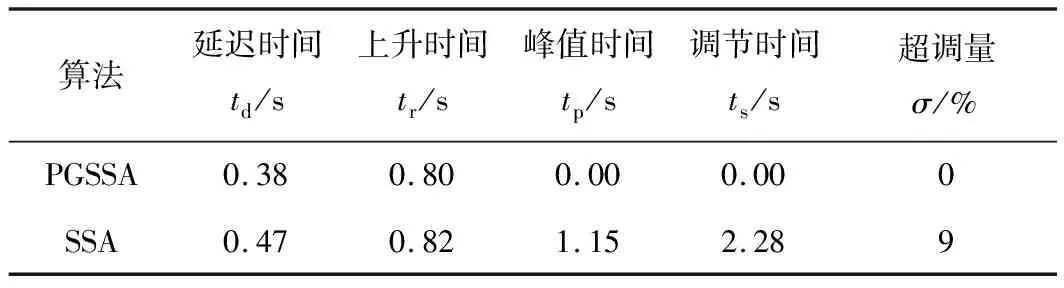
表2 階躍響應性能指標

通過表1和圖4，可以了解到基于粒子群算法改進的麻雀算法整定優化ADRC控制系統參數的收斂速度和收斂精度要優于普通的麻雀群智能算法。而從表2和圖5無擾動階躍曲線，PGSSA算法整定后的ADRC控制系統在延遲時間和上升時間要小于SSA算法整定后的控制系統，而且還沒有出現超調量和震蕩，處于穩定輸出狀態。

4.2 ADRC有擾動仿真

在4.5～5.5 s期間存在u0=2.2的擾動，對控制系統進行仿真，階躍響應曲線如圖6所示。

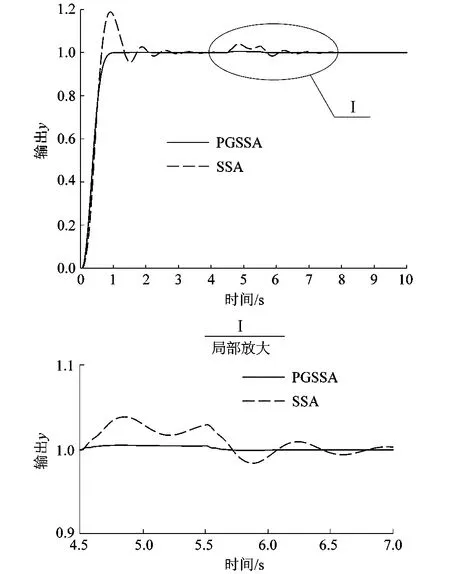
圖6 有擾動階躍曲線

由圖6可知，PGSSA算法整定后的控制系統對擾動有很強的抑制作用，在擾動消失后，系統能很快穩定下來，且沒有出現大的震動和超調量；而SSA算法整定后的系統，在擾動出現后有較大超調量和4次振蕩，且在擾動消失后經歷約1.5 s才重新穩定下來。

4.3 PID有擾動仿真

PID控制系統在4.5～5.5 s期間存在u0=2.2的擾動的階躍響應曲線如圖7所示。

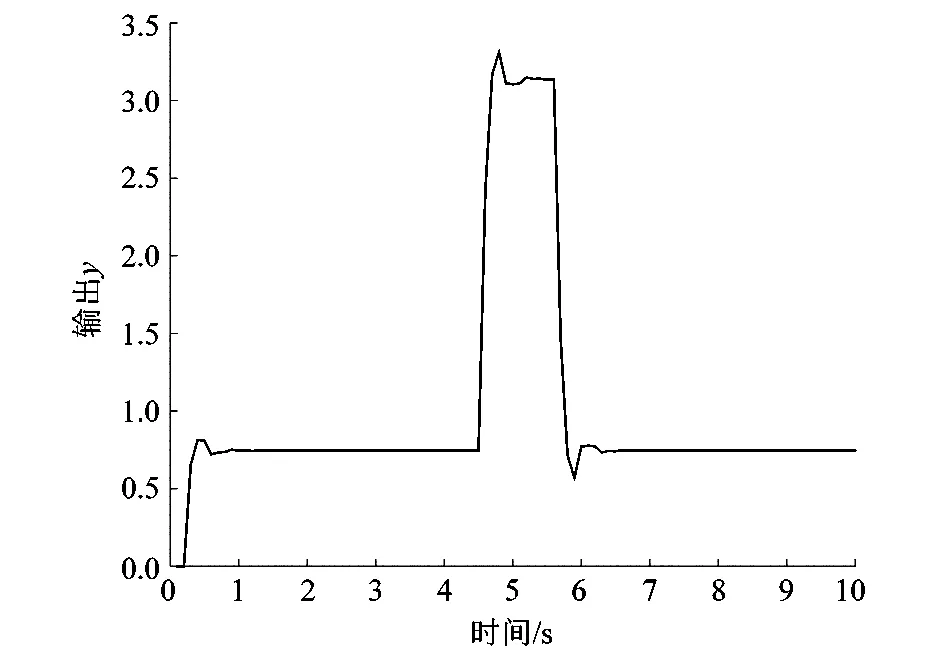
圖7 PID有擾動階躍曲線

由圖6～7中的ADRC擾動階躍曲線和PID擾動階躍曲線可分析出，PID控制系統對擾動沒有很好的抑制作用，而且擾動存在期間對輸出也有很大的影響，擾動消失后經過1 s左右進入穩定。在相同時間出現同樣的擾動時，ADRC控制系統明顯比PID控制系統對擾動抑制作用強，而且在擾動消失后能更快更平穩地進入穩定狀態。

5 結論

課題組通過建立復卷機收卷端張力控制運動數學模型，分析其主要受到放卷輥上卷材的線速度和卷徑的影響，設計采用閉環轉矩張力PADRC控制方法，構建穩定的張力控制系統。

針對PID控制器的缺點，選擇利用ADRC作為控制器。經過仿真對比發現，PID控制系統對大擾動調節時間慢，沒有有效地減弱擾動對系統輸出的影響。而ADRC控制系統對擾動有很強的抑制作用，而且擾動消失后調節速度快。

針對SSA算法以跳躍方式搜索和易陷于局部最優的缺陷，提出引入粒子群算法中的速度算子以速度v的移動方式進行搜索，以免忽略某些較優值；并且采用遺傳算法中的交叉和變異操作，用來保持麻雀種群的多樣性，以增強算法的全局搜索能力。在對PGSSA算法和SSA算法分別進行整定仿真，可以得出，在同樣的初始條件下，PGSSA算法在收斂速度和收斂精度都要優于SSA算法，而且PGSSA仿真得出的階躍響應的性能指標(如延遲時間、上升時間及超調量等)也比較優越。