發現千千萬 起點是一問

夏春芳

[摘 ?要] 培養學生發現問題與提出問題的能力是小學數學的重要教學目標之一。文章通過理論研究與教學實踐，探索培養學生發現問題與提出問題的能力的教學實踐路徑：創設生活情境，創建“數學廣角”， 留足時間與空間。

[關鍵詞] 發現;提出;問題;小學數學

“發現千千萬，起點是一問。”問題是思考的源動力，也是創新的基礎，培養學生發現問題與提出問題的能力是小學數學的重要教學目標之一。實際上，學生發現問題與提出問題比分析問題和解決問題更重要，因為很多創造往往是從發現問題開始的。從目前課堂教學現狀來看，大多數問題都是課本或是教師提出，真正由學生主動提出的問題數量很有限。如何引導學生發現并提出有價值的問題呢？筆者將通過理論研究并結合自身工作經驗，論述在小學數學課堂中培養學生發現問題與提出問題的能力的基本策略，以期能取得拋磚引玉的效果。

[?] 一、創設生活情境，引導學生發現、提出問題

實踐證明，當學習的材料來自現實生活時，數學才是活的、富有生命力的。生活情境指的是教師把教學內容融入生活，從而創設出的一種富有趣味性、真實性等的學習情境[1]。教學中，教師創設生活情境，能激發學生的探究欲望，使學生產生一種強烈的想知道“是什么”“為什么”的沖動，進而引發學生主動發現問題、提出問題。

比如，在教學“平行四邊形不穩定性”時，筆者以學校的伸縮門為例創設生活情境。

師：同學們，你們注意觀察學校的伸縮門了嗎？它是由什么圖形組成的？

生（齊）：平行四邊形。

師：你們還見過生活中有哪些平行四邊形的物體呢？

生1：我們家的伸縮衣架也是由平行四邊形組成的。

生2：為什么伸縮門、伸縮衣架都要設計成平行四邊形呢？

師：這個問題提得好。現在，讓我們通過實驗來進行研究。

隨后，筆者讓學生拿出課前用吸管和絲線串成的平行四邊形，讓學生拉動平行四邊形的兩個對角，使它變成不同的形狀。在反復拉動的過程中，學生體驗到了平行四邊形的不穩定性。然而，這種看似嚴謹的數學操作卻并未打消學生對平行四邊形不穩定性的疑慮。一個學生提出這樣的問題：“在我家墻上掛著一個平行四邊形的木板裝飾畫，我取下來玩過幾次，并用力地拉動它的四個角，發現它根本就不容易變形。這又該怎么解釋呢？”這個時候，筆者要求學生以小組為單位用完全相同的四根小棒擺出平行四邊形，結果他們發現每一個小組擺出的平行四邊形的形狀都各不相同。筆者趁勢總結道：“我們已經知道，三角形的穩定性指的就是一旦確定了三角形的三條邊，那么，它的大小和形狀就完全確定了。同樣的道理，平行四邊形的不穩定性指的是盡管確定了平行四邊形的四條邊，但是它的大小和形狀卻依然會發生變化。”至此，學生才準確、全面地理解了平行四邊形的不穩定性。

教學中，筆者通過學校的伸縮門創設生活情境，調動了學生已有的生活經驗，激發了學生思考的主動性和探究的興趣。在現實生活中，伸縮門是平行四邊形，伸縮衣架也是平行四邊形，有了這樣的經驗積累，學生提出“為什么伸縮門、伸縮衣架都要設計成平行四邊形呢？”這一問題水到渠成。此外，在筆者通過伸拉實驗初步闡釋平行四邊形不穩定性的基礎上，學生結合生活經驗又進一步提出了頗有探究價值的問題，這就為教學的進一步探索指明了方向。筆者引導學生通過操作理解平行四邊形不穩定性的內涵，從而使學生的認知層次提升了一個臺階。由此可見，創設生活情境有助于學生“有感而問”，在探究的過程中，學生又會產生新的疑問，由此形成一個以提問、探究、釋疑又再次回到提問的良性循環。

[?] 二、創建“數學廣角”，引導學生發現、提出問題

這里所說的“數學廣角”指的是在班級中創建的一個供學生討論研究數學問題的專門區域。值得注意的是，學生發現問題、提出問題并非總是集中在教師授課的過程中，學生在課下用數學知識解決問題時，或是與同學探討交流時也會產生各種疑問[2]。因此，要提高學生發現問題與提出問題的能力，教師可以采取建立“數學廣角”的方法，讓學生把遇到的問題集中起來，寫在問題檔案卡片上，并粘貼在“數學廣角”的區域，供同學們共同探討交流。在此基礎上，教師可以在課上留出時間來專門引導學生共同探討、解決一些典型的、具有研究價值的問題，消弭學生思維的困惑，進一步建立學生發現、提出問題的信心。

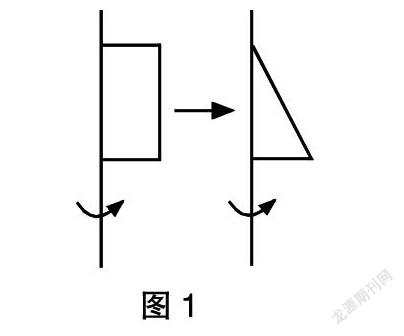
比如，在講解“圓錐的體積”時，有的學生在“問題檔案卡片”上記錄了這樣的問題：“圓柱是由長方形旋轉得到的，而與它等底等高的圓錐則是由圖1中的三角形旋轉得到的，不難看出，三角形的面積是長方形的面積的1/2，所以我認為圓錐的體積應該是它等底等高的圓柱體積的1/2，而不應該是1/3。”為了弄明白這一問題，學生紛紛提出了自己的看法。有的學生提到：“旋轉的平面圖形的面積和旋轉后形成的立體圖形的體積之間并沒有直接關系。”有的學生提到：“面積和體積是不同的概念，二者之間沒有數量上的關系。”而有的學生則更進一步地提出：“比如一個長方形的長是4厘米，寬是3厘米，以長為軸旋轉出的圓柱體積與以寬為軸旋轉出的圓柱體積是不同的，這就說明盡管是同一個圖形，不同的旋轉方式得到的立體圖形的體積也是不相同的，面積和體積二者之間并無直接關聯。”

學生將課中、課后以及與同學交流時發現的問題記錄在“問題檔案卡片”上，為進一步的探索提供了絕好的素材。“真理越辯越明”，正是在你一言我一語的討論和交流中，學生的認識逐漸變得清晰起來，思維的困惑自然也就不復存在。建立“數學廣角”，不但可使學生學會提問，學會思考，還可促進學生對知識的深度理解，提升學生的學習力。

[?] 三、留足時間與空間，引導學生發現、提出問題

清代鄭燮曾說過：“讀書好問，一問不得，不妨再問。”可見，主動發現問題、提出問題在學習過程中具有至關重要的作用[3]。然而，在傳統教學中，教師過分關注知識的傳授和灌輸，學生處于被動學習的地位，一般是教師講到哪里，學生就聽到哪里，學生缺乏自己的思維時空，無暇去發現問題、提出問題。因此，在教學中，教師的“教”要讓位于學生的“學”，教師要由“臺前”轉向“幕后”，要預留一定的空間運用啟發性語言，為學生的問題萌發創造機會，把原本教師想要提出的問題改為讓學生主動發現和提出，進而使學生體驗到發現問題、提出問題、分析問題、解決問題的全過程。

師：我們剛學習的百分數和以前學過的什么知識比較相似？

生1：和分數比較相似。

師：那么，關于二者之間的關系，你們有什么疑問嗎？

（學生思考。）

生2：我們已經學習了分數，為什么還要再學習百分數呢？

生3：與分數相比，百分數有什么優勢呢？

師：誰能談一談自己的看法呢？

生1：我認為百分數更形象一些。比如在比較升學率（48%和56%）的時候，很容易就能夠想象到把單位“1”平均分成100份，56份比48份要多一些，而如果用分數就需要進行通分才能比較，比較麻煩。

生3：分數后面可以帶單位，百分數可以帶單位嗎？

生2：百分數不能帶單位。

師：為什么呢？

生2：百分數表示的是兩個數的倍比關系，而分數既可以表示兩個數的倍比關系，也可以表示具體的量，在分數表示具體量的時候，是可以帶單位的，比如可以說米，但不能說成80%米。

生4：我們在學習分數的時候需要把分數化成最簡，為什么百分數卻不需要化簡呢？

……

教學中，筆者充分發揮了學生的主體作用，在明確了學生提問方向（百分數與分數的異同點）的前提下，為學生預留出充足的提問、探討的時間與空間，在師生之間、生生之間的對話和交流中，學生的思維被激活。在生疑、質疑、釋疑的過程中，新知識自然地納入原有的知識體系之中。

提出一個問題，永遠比解決一個問題更重要。在教學中，教師可創設生活情境，建立“數學廣角”，留足時間與空間，引導學生在觀察和思考中主動發現、提出問題。在此基礎上，教師需要再讓學生對問題展開分析和探索，最終促進問題得到解決，使學生體驗問題從產生到解決的全過程，進而提升學生的數學素養。

參考文獻：

[1] ?李永芬. 在數學教學中培養學生提出問題的能力[J]. 廣西教育，2020（41）：137，139.

[2] ?曹春艷，穆敏娟，肖虹，等. 小學數學課堂提問現狀調查研究：基于教師與學生雙視角的分析與思考[J]. 小學教學（數學版），2020（9）：4-7.

[3] ?朱國榮. “求學問，需學問”：落實“增強發現和提出問題的能力”之思考[J]. 教學月刊·小學版（數學），2018（Z1）：11-15.