激光測量系統不確定度最小包絡橢球模型研究

李 源，柴艷紅，劉蘭波，毛 喆，翟新華

(上海航天電子技術研究所，上海 201109)

引 言

當前數字化的測量手段蓬勃發展，測量精度逐步提升，應用也愈發廣泛。其中激光測量系統，例如激光跟蹤儀、激光雷達等在諸多領域得到了廣泛應用[1-3]。特別是在航空、航天、船舶等大型的制造業領域，產品的尺寸越來越大，加工、裝配等工藝的精度要求也越來越高[3-5],其中激光測量系統得到了非常廣泛的應用。在精密測量與大尺寸測量的問題中，測量系統獲得的坐標通常不能直接應用于相關指標的計算與裝配的分析，而是需要開展相應的測量誤差分析與裝配坐標系轉換。激光測量系統的誤差，通常設備會給出具體值，例如某型號激光跟蹤儀的標稱不確定度為15μm+6μm/m，即基礎誤差為15μm,測量距離每增加1m,其誤差增加6μm。隨著實際應用場景提出了越來越高的需求，僅僅是測距方向上的最大誤差已經很難滿足很多測量場景的測量設計與實施指導。測量不確定度在各個方向上的各向異性，即具體在測量空間的3維分布，對測量以及加工與裝配實施中的重要精密指標確定已經產生了影響，甚至進一步對測量設備的布局提出了要求[6-11]。當前一系列的研究主要通過復雜的優化模型，例如迭代最近點法(iterative closest point,ICP)、奇異值分解法(single value decomposition,SVD)、蒙特卡洛(Monte Carlo,MC)數值估計等，來對變換參量進行優化，隨后分析這一系列的模型中的誤差傳遞，通過數值仿真的思路進行特定點的不確定度分析[6,9-10,12-16]。然而為了結合設備的狀態與實測的場景，往往需要針對復雜的模型開展重復的大量優化計算，這無疑對現場測量帶來了很大的不便。而計算獲得的大量仿真點或者不確定度模型往往也需要與實際的特定點大量測量數據進行數據篩選、模型坐標變換匹配與誤差比對。當前對于大量數據篩選依然主要為面向擬合目標的分析而非脫離應用的誤差分析[17]。因此，需要提出以更高效的算法準確地篩選獲取基于大量實測或者仿真點數據的最小包絡模型，即不確定度模型。

孤立森林算法(isolated forest algorithm，IFA)是一種基于數據空間隨機切分迭代的異常值檢測方法。該算法通過隨機超平面在數據空間內進行切分，并將切分后的子空間以二叉樹進行數據結構構建。對每個子空間進行相同的隨機切分并構成子樹(分枝)，直至每個分枝有且只有一個數據。通過在樣本空間多次隨機采樣并構建系列數據樹，形成數據森林。通過判定數據空間中每個點距離數據樹根部的深度評估其異常程度，并據此進行數據篩選。該算法已經廣泛應用于各領域的異常檢測、數據清洗等過程[18-21]。粒子群優化(particle swarm optimization，PSO)算法是一種更偏重于群體智能的優化算法。其將待確定問題的集合作為一個粒子，并以粒子群模仿鳥群覓食的行為特征在解空間進行探索。每個粒子結合自我認知與群體經驗交流，遵循相同的規則進行運動。區別于傳統優化算法，該算法具備較強的跳出局部最優解的能力，并已經廣泛應用于了函數優化、神經網絡訓練、決策、建模等諸多領域[13,22-27]。

本文中的研究以激光跟蹤儀系統為研究對象，以單點測量實驗出發，引入了孤立森林算法對不確定度測量數據進行處理與分析，并采用粒子群優化算法進行最小包絡橢球計算，高效快速準確地獲取該設備的單點測量不確定度分布情況。該方法僅基于單點的測量數據，因此可以應用于各型號的激光跟蹤儀以及激光雷達等其它激光球坐標測量系統的不確定度分布測試實驗，甚至MC模型的仿真數據分析。以此為基礎，可以通過測量與仿真數據分析獲得3維空間內不同位置的不確定度分布，因此,本研究具有進一步指導測量場景布局設計等重要意義。

1 激光測量系統的不確定度分布模型

本文中的研究對象為Leica At-930激光跟蹤儀。以測量位置靶球中心為原點可以建立不確定度橢球坐標系(uncertainty ellipsoid coordinate system，UCS)，在此坐標系(w,u,v)下不確定度橢球包含的范圍可以描述為方程：

(1)

式中，w,u,v是測量點在UCS三坐標軸w,u,v上的坐標值，a，b，c分別是該不確定橢球的三軸半軸長。圖1為UCS下不確定度橢球示意圖。

Fig.1 Schematic diagram of uncertainty ellipsoid under UCS

在實際測量中，靶球的位置會隨著測量目標的變化而變化，即各測量點分別存在其獨立的UCS，因此,測量數據往往采用統一的基于跟蹤儀的測量系統坐標系(measurement coordinate system， MCS)。對于任意UCS其坐標軸單位向量在MCS上可以描述為：

(2)

式中，α為方位角，β為天頂角，w為測量的激光方向，v為w與z平面上垂直于w的方向，u為遵循右手定則垂直于w與v的方向。由UCS到MCS的旋轉矩陣則可以描述為：

(3)

圖2為激光跟蹤儀MCS與坐標系UCS的轉換示意圖。

Fig.2 Coordinate system conversion of laser tracker between MCS and UCS

對于測量點P，在其位置構建的UCS在MCS上的位置矢量可以描述為：

(4)

式中，x0，y0，z0為在該位置累積測量采樣分布的期望，以其近似為理論靶球中心。據此兩坐標系變換的變換矩陣可以描述為：

(6)

據此依據通用坐標系轉換公式：

(7)

式中，A,B作為通用坐標系表達均可以替換為MCS或UCS，據此任意測量位置在MCS下的累積采樣位置數據均可以通過坐標變換轉換為UCS下進行標準不確定度橢球的分布分析；而分析獲得的不確定度橢球同樣可以轉換為MCS下測量場不同位置的橢球分布。

2 最小不確定度包絡橢球模型

2.1 孤立森林算法數據篩選

基于固定設備與采樣點位的單點重復位置測量與基于蒙特卡洛等算法的單點位隨機仿真測點均是獲取單點位置不確定度分布的重要方法。這些方法可以獲得對于單點的大量測量/仿真位置數據，實測過程中由于場地與設備等因素的擾動會獲得極少數較大的誤差點，而在算法仿真中同樣會由于必要的擾動函數產生少量較大誤差點。在進行不確定度包絡橢球計算時，這些較大誤差點會對包絡計算形成干擾，使得最終獲得的包絡橢球過大。本研究中，引入了孤立森林算法來對測量/仿真數據進行采樣篩選。

基于本課題問題研究，孤立森林算法模型可以通用化描述為{D,F,H,fs,rs,Nt,Nsub,nDFR}，其中D={P1,P2,…,PN}為數據空間，包含所有的待分析篩選的數據，其數據個數為N，對于每個數據點P，其維度為d，在本研究問題中，D即為所有測量/仿真位置數據的集合，維度d=3；F={T1,T2,…,TNt}為孤立森林算法劃分出的森林，其中T為森林中的獨立數據樹，Nt為每座森林中樹的個數；對于每個數據樹T包含集合Dsub={Pr,1,Pr,2,…,Pr,i…Pr,Nsub}的全部數據，并通過孤立函數fs劃分為二叉樹結構，Nsub為每棵樹的數據個數，Pr,i為數據空間中隨機出的第i個數據；Dsub為每棵樹的數據集合，其為D的隨機樣本量是Nsub的子集；孤立函數fs可以描述為：

(8)

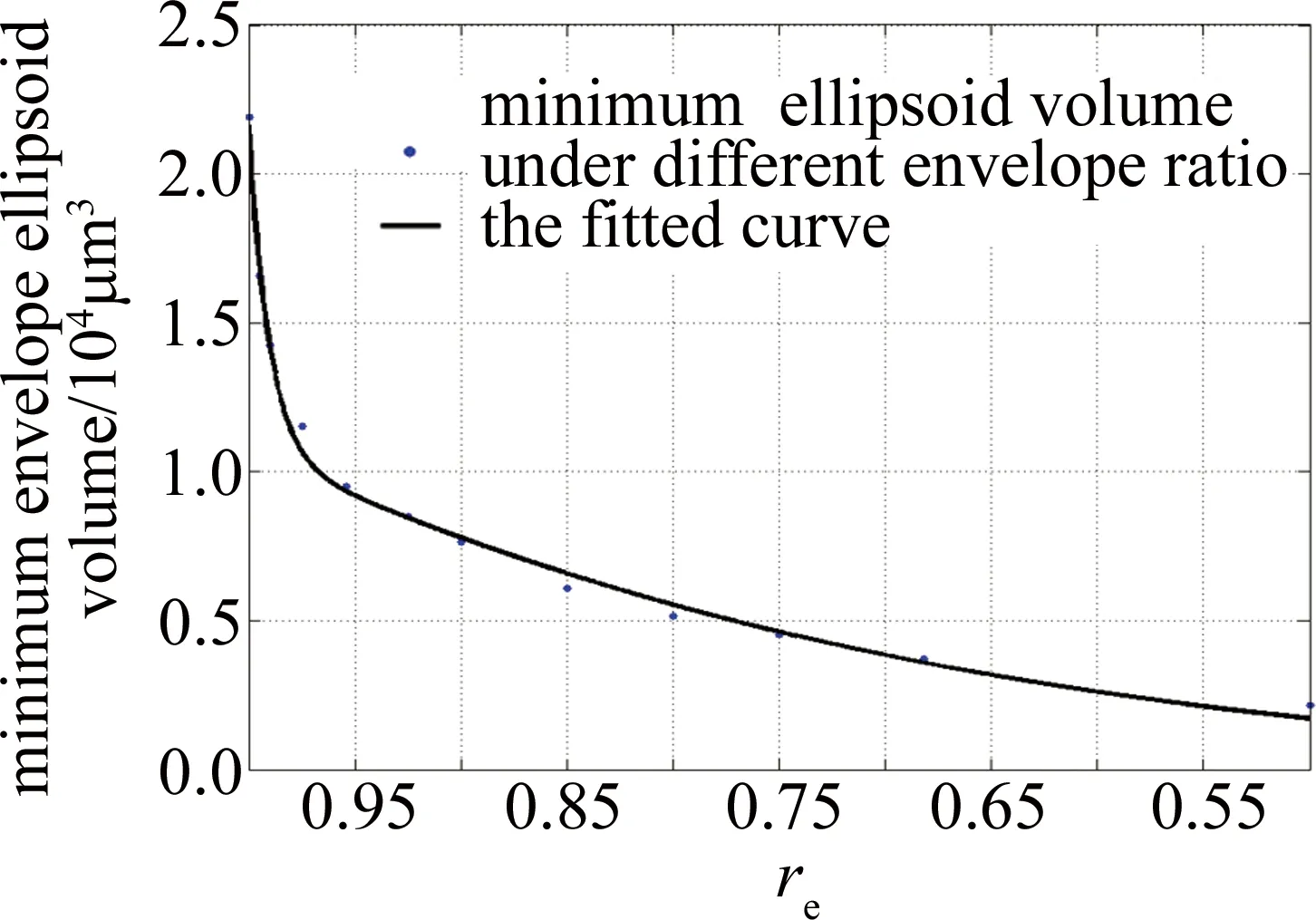
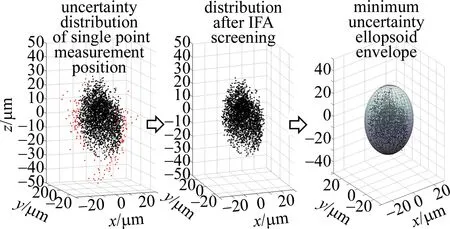
式中，Dsub,l,h與Dsub,r,h分別代表該數據樹在距離根部深度為h(即h層)的左右數據子集；Sr,h為該數據樹在h層數據孤立分割的標準，其取值為[min(Dsub,h),max(Dsub,h)]范圍內的隨機值；因為D為d維的數據集，在孤立分割時，取隨機整數rd∈[1,d]作為分割判定時的比較維度，Pr,i(rd)即為數據Pr,i在比較維度rd下的數據分量。在篩選計算中,將后續的Dsub,l,h+1,或者Dsub,l,h+1分別作為新的子數據集Dsub,h+1,采用孤立函數fs進行遞歸迭代劃分，直到最終層次的Dsub樣本量為1，即完成數據樹的構建。H為每個數據點在森林中每個樹上距離根部的深度的平均值的集合；rs為算法的篩選次數，即森林的個數；nDFR則為每次篩選時判定標準，即數據距離根節點的深度(deep from root,DFR)，即當H(Pi)

2.2 粒子群優化最小包絡橢球模型

通過坐標轉換與數據篩選后的測量/仿真位置數據可以通過PSO基于(1)式進行最小包絡橢球模型的建立。在UCS下，橢球中心為原點，因此最小包絡的控制因素則為橢球三軸的半軸長。定義粒子X={a,b,c}，解的搜索空間為3維。在解空間隨機生成n個粒子，每個粒子Xi均為該系列數據的潛在一個包絡橢球解。隨著迭代時刻t的推進，每個粒子均在解空間以一定速度Vi運動探索以獲取最優的包絡解。每個粒子的運動規則遵循：

Vi,t+1=ω·Vi,t+c1r1(Li,t-Xi,t)+

c2r2(Gt-Xi,t)

(9)

Xi,t+1=Xi,t+Vi,t+1

(10)

式中，Xi,t與Vi,t為第i個粒子在t時刻的位置與運動速度；Li,t為第i個粒子到t時刻其個體運動軌跡中的最優解，代表著粒子的個體認知；Gt為t時刻所有粒子運動軌跡中的最優解，代表著粒子的群體交流與共識；ω為慣性因子，c1和c2為學習因子，控制著粒子向自身經驗和群體經驗學習的傾向，r1和r2為隨機因子，為[0,1]之間的隨機數。在每次運動迭代完成后，粒子Xi,t均以適應值函數fe來進行評價，通常適應值越小，該粒子距離理論最優解越近。本研究中以包絡橢球解的體積作為評價標準，因此對于粒子Xi={ai,bi,ci}：

(11)

式中，re為橢球模型對數據D0的包絡比例，N0為D0中數據的個數，nin為D0中處于包絡范圍內的數據個數，可以描述為：

(12)

式中，argnum函數的輸出結果為滿足后續條件的數據Pi個數，EXi(Pi)為點Pi代入粒子Xi條件下的包絡橢球模型E(見(1)式)計算其相對于橢球包絡面的位置。通過適應值函數，在每次粒子群運動迭代后對個體歷史最優解Pi與全局最優解G進行更新：

(13)

(14)

式中，argmin函數的輸出結果為使得適應值函數fe最小的粒子Li。

在本研究問題算法執行流程為對所有粒子在粒子空間進行隨機位置初始化，通過(9)式～(14)式對每個粒子的運動位置與速度的迭代計算完成最優包絡的探索。區別于傳統優化問題，最小包絡的探索在(11)式～ (13)式中存在對包絡數據比例的判定，因此為實現優化探索的準確性與效率，需要選擇合適的初始化粒子位置范圍與粒子陷入過小包絡模型局部位置后的擾動逃逸模型。粒子初始化位置為：

Xi=(wmax,umax,vmax)·rx(l0)

(15)

式中，wmax，umax，vmax為UCS下所有點在三坐標軸下的絕對值極值，rx為[1,l0]范圍的隨機值，l0為空間放大系數。擾動逃逸函數在當前粒子無法滿足包絡要求時可以替代其位置更新函數，描述為：

Xi,t+1=Xi,t·es+Vi,t+1|fe(Xi,t)=-1

(16)

式中，es為逃逸系數。

3 實驗驗證與結果討論

研究采用LeicaAt-930激光跟蹤儀以及3.81cm的跟蹤儀靶球，進行固定機位與靶球位的單點多重數據測量采集，并將數據應用于孤立森林模型數據篩選與最小包絡橢球求取，以驗證模型的有效性。

3.1 測量采樣篩選

固定跟蹤儀設備，在距離設備約4.7m的固定靶球位置的單點采集N=3091個位置坐標值。孤立森林篩選次數rs=10，森林中數據樹的數目Nt=100，每棵樹的數據量Nsub=256。由圖3可知，采樣點云分布即為橢球型，但也能發現存在系列遠離點云的少量誤差較大點。nDFR=4時，保留采樣點依然為100%，舍棄誤差點數量為0，即所有點在數據樹上的平均高度均大于4；當nDFR取為6和7時，依然存在少量誤差較大點保留；當nDFR>8時，較大誤差點已基本被去除，隨著nDFR值增大，橢球周邊點分布密度較小的區域也逐漸被去除，保留的采樣點比例逐步減小。

將篩選后的數據點進行三軸及橢球體積的包絡橢球分析,re=0.99時的結果如圖4、圖5所示。圖4中百分比為篩選后有效數據占原全部數據的比例，軸長變化曲線均采用了雙高斯擬合。篩選后有效數據比例由100%減小到約95%的過程，包絡橢球u，v軸半軸長度減小速率較快，這說明較大誤差點是分布在u，v軸方向離中心較遠的位置。篩選保留比例減小到95%以下后，包絡橢球u，v軸半軸長減小曲線符合高斯曲線，即去除掉較大誤差點后，采樣點在u，v兩軸的密度分布為由中心向外的高斯分布。對于w軸，隨著篩選后有效數據比例由100%減小到約95%，w軸半軸長隨之增大，這是因為加大誤差點是在在u，v軸方向離中心較遠的位置，其在w軸上投影較小，過大的u，v軸長使得包絡橢球更呈現扁而長寬的形狀。隨著誤差較大點的去除，u，v軸長急劇減小，為使得中央高密度點云分布能夠完成包絡，w軸長會呈現增長的趨勢。而隨著有效比例到達95%到約80%，由于較大誤差點已經基本被去除，w軸半軸長開始逐漸減小，但此時其減小的趨勢遠小于另外兩軸，這是因為點云主要在u，v軸方向延伸分布，存在點云密度相對較低的包圍區域，這些點的去除對w軸軸長的影響相對較小。隨著比例減少到80%以下，點云的篩選到達核心區域，此時w軸軸長的減小同樣符合高斯曲線，即在核心點云分布區域w軸方向點密度分布也是呈高斯分布。結合以上分析，孤立森林數據篩選標準nDFR的最佳取值為8，篩選后有效數據比例保持為94%左右。當nDFR=8時，進一步分析不同采樣點數的篩選比例，如圖6所示。當N>250時，篩選后有效數據比例即會穩定在94%左右。

Fig.4 Screening ratios and envelope ellipsoid models from effective data realized by different DFR

Fig.5 Characteristic changes of envelope ellipsoid with different screening ratios

Fig.6 Change curve of the screening ratio with the total number of samples when DFR is 8

3.2 不確定度橢球

對于篩選后的有效數據，采用PSO進行最小包絡橢球計算。在計算中，模型中粒子運動慣性因子ω=1，學習因子c1=c2=0.2，空間放大系數l0=15，逃逸系數es=2，粒子數為30個。

選取終止條件為計算到達最大迭代次數T=100000，包絡比例re=0.99進行模型收斂測試。在Intel i5-6400 CPU 2.7GHz與8GB內存條件下，孤立森林篩選與最小包絡橢球計算共耗時約為16.5min，其適應值的歸一化收斂曲線如圖7所示。本次計算迭代到達5156次即實現最終收斂。以最終收斂結果為標準，本次計算迭代達到1354次時，收斂率達到99.88%，迭代達到2116次時，收斂率達到99.96%。據此，在最小包絡橢球計算中，其終止條件可以設為達到最大迭代次數T=10000，經測試在上述計算設備條件下耗時不高于2min。在快速計算中，其終止條件可以設為最大迭代次數T=3000，經測試在上述計算設備條件下耗時不高于50s。

Fig.7 Convergence process of fitness value in minimum envelope ellipsoid calculation(within 2500 iterations)

在實際測量測試中，會根據測量需求的精度要求選取由橢球中心向外不同置信區間進行測量規劃設計，而最小橢球包絡算法同樣可以支持不同包絡比例的不確定度范圍計算，如此可以更直觀地描述3維不確定度的概率密度分布。如圖8所示，當re=1時，即所有經篩選后的點全包絡，減小re取值可以得到相應比例包絡條件下的不確定度橢球模型。圖9為不同包絡比例下橢球模型的體積變化，其擬合為雙高斯分布。在包絡比例re≈0.975時，其包絡范圍即為核心點云區域，這與系列模型研究相符[7]。

基于以上分析，圖10即為基于最小橢球包絡的不確定度模型的計算方法流程:(1)針對特定點進行點云測量/仿真；(2)孤立森林算法采樣點篩選；(3)進行PSO不確定度橢球包絡模型建立。以此方法，距離4.7m的位置的共計3091個點測量數據，經過nDFR=8

Fig.8 Minimum envelope ellipsoid model with different envelope ratios

Fig.9 Curve of minimum envelope ellipsoid volume with different envelope ratios

Fig.10 Calculation method of uncertainty model based on minimum ellipsoid envelope

條件下的孤立森林算法篩選保留了2912個有效數據；通過re=0.975包絡比例的粒子群10000次計算迭代，最終最小不確定度橢球包絡三軸長為：a=4.95μm，b=18.39μm，c=30.53μm；計算總耗時121s。

3.3 不確定度場分布

為直觀測量空間中各位置激光跟蹤儀的不確定度分布，設計了如圖11所示的實驗。固定跟蹤儀機位，在測量場地內規劃處不同距離與測量方位的測量點；每個測量點以相同高度(約1.2m)固定靶座；對每個測量點分別進行多次重復測量；對每個測量位置的點云進行孤立森林篩選；篩選后的點云轉移到該點位的UCS下進行PSO最小包絡橢球模型計算；將獲取的最小包絡橢球轉換到統一的MCS下，即得到空間各位置的不確定度分布。如圖12所示，為了方便直觀觀察各位置的不確定度橢球形貌與姿態，圖中的不確定度橢球以6000倍軸長呈現。圖12a為測量空間的俯視圖，可以看到，不確定度橢球的空間姿態得到了很好的還原；從圖12b可直觀看到，該空間內不同位置的橢球尺寸變化，不確定度最主要受測量距離的影響。

Fig.11 Experiment design of uncertainty test of laser tracker

Fig.12 Uncertainty ellipsoid model distribution of different measurement positions (displayed by ellipsoid axis length magnified 6000×)

4 結 論

針對激光跟蹤儀測量系統建立了其不確定度橢球模型，構建了面向橢球包絡計算的不確定度橢球坐標系與面向場景分析的測量場坐標系，并提出了通用的轉化模型。基于孤立森林算法構建了面向大量測量/仿真數據的有效數據篩選模型。基于粒子群優化算法建立了面向篩選后數據的最小橢球包絡計算模型。針對當前航天有效載荷與天線系統大量應用的10m尺度量集，開展了特定點數據測量與測量場地不同位置的測量數據的分析與計算。模型高效準確地將測量的點云數據轉化成特定點的不確定度橢球模型，并再現了其在測量場內的分布與姿態，這充分驗證了數據篩選與最小橢球包絡模型的有效性，也證明了模型的在不同條件下的適用性。這對高效快速準確地獲取激光測量設備在3維測量空間內的測量不確定度分布情況，并對進一步完成高效地測量布局分析、設計研究具有重要意義。

該模型在針對其它激光球坐標測量系統、更大尺度量級以及面向多站、轉站以及多系統聯測角度的不確定度分析中均具有很強的應用潛力，這也是后續研究開展的重要方向。