白盒SM4的中間值平均差分分析

張躍宇，徐 東，蔡志強，陳 杰

(1.西安電子科技大學 網絡與信息安全學院，陜西 西安 710071；2.西安電子科技大學 綜合業(yè)務網理論與關鍵技術國家重點實驗室，陜西 西安 710071；3.中國人民解放軍66061部隊，山西 陽泉 100141；4.桂林電子科技大學 廣西密碼學與信息安全重點實驗室，廣西 桂林 541004)

2002年，CHOW等[1]首次提出白盒安全模型，該模型下的攻擊者對算法運行環(huán)境具備完全的控制權。算法細節(jié)以及運行過程完全暴露在攻擊者的視野中，攻擊者的能力包括動態(tài)觀測算法程序運行過程、修改算法運行過程的中間值、對算法程序進行調試分析等。為了保證在白盒安全模型下密碼算法的密鑰安全性，需要對密碼算法進行白盒化處理，處理后的算法稱為白盒實現(xiàn)。一般的白盒化方法是用嵌入密鑰的查找表網絡來代替原計算過程，采用混淆手段對查找表進行保護，同時使用外部編碼對整個實現(xiàn)進行保護。白盒化方法由CHOW等在其白盒AES[1]、白盒DES[2]方案中首次提出并使用，后續(xù)提出的大多數(shù)白盒實現(xiàn)也是基于該方法實現(xiàn)的。

白盒安全性模型中密碼算法的運行過程與設計細節(jié)完全被攻擊者所掌握，因此攻擊者可以依據(jù)算法設計的缺陷，采用仿射等價、線性等價等手段對算法內部的混淆進行剝離，對混淆剝離后的查找表進行分析，進而提取出密鑰信息。典型攻擊方法的代表有BGE(olivier Billet-henri Gilbert-charaf Ech-chatbi)攻擊[3]、MGH (MICHIELS w-GORISSEN p-HOLLMANN h d)攻擊[4]等分析手段。

2016年，BOS等[5]將差分功耗分析應用于白盒實現(xiàn)的軟件分析中，首次提出差分計算分析(Differential Computational Analysis，DCA)。差分計算分析不需要攻擊者全面掌握算法細節(jié)，只需采集白盒實現(xiàn)程序運行過程中的相關變量，通過相應的統(tǒng)計分析方法即可提取出密鑰信息。差分計算分析的效率更高，部署更加簡便。由于差分計算分析的便捷性與高效性，差分計算分析從首次提出便取得了廣泛關注。文獻[6-7]對差分計算分析進行了解釋與介紹，給出了該分析方法成功進行的理論原因。文獻[8]中又提出了改進差分計算分析效率的方法。2019年，RIVAIN等[9]研究了內部編碼對差分計算分析的影響，并提出了類似的分析手段；同年，BOGDANOV等[10]又提出了高階的差分計算分析方法，用以分析含有軟件補償對策的白盒實現(xiàn)。

SM 4算法是我國商用密碼標準算法[11]。2009年，肖雅瑩等[12]提出了第一個SM 4算法的白盒實現(xiàn)方案(肖-來白盒SM 4)，該方案利用CHOW等的白盒化思想，將SM 4算法流程轉換為查找表網絡，并采用線性編碼對查找表進行保護。2013年，林婷婷等[13]結合BGE攻擊、差分分析等方法，成功對肖-來白盒SM 4進行了分析。2015年，SHI等[14]提出一種新的白盒SM 4方案，將SM 4算法步驟結合到查找表中，并利用線性編碼對查找表進行保護。同年，BAI等[15]又在肖-來SM 4方案的基礎上，將查找表的編碼復雜化，提出了一種新的白盒SM 4實現(xiàn)BAI-WU(白-武)白盒SM 4。2018年，潘文倫等[16]對肖-來白盒SM 4以及BAI-WU(白-武)白盒SM 4的安全性進行了分析，給出了密鑰空間。2020年，姚思等[17]結合混淆密鑰與查找表技術，提出了一種新型白盒SM 4實現(xiàn)。作為首個提出的白盒SM 4方案，肖-來白盒SM 4的白盒化方法與查找表混淆手段在后續(xù)提出的白盒SM 4方案中都得到了借鑒與應用。

筆者在對差分計算分析進行研究的基礎上，首次將差分計算分析用于白盒SM 4的安全性分析，提出了一種針對白盒SM 4的分析方法。該分析方法利用加密過程中所產生的所有中間查表結果，采用均值差分的方法，使用線性組合抵消白盒SM 4中的混淆，稱該分析方法為中間值平均差分分析(Intermediate-Values Mean Difference Analysis，IVMDA)。并利用IVMDA實現(xiàn)了肖-來白盒SM 4的密鑰提取。

1 SM 4白盒實現(xiàn)方案

肖-來白盒SM 4算法的基本結構與標準SM 4算法結構大致相同：分組長度為128 bit，采用32輪非線性迭代結構；密鑰長度為128 bit，通過密鑰拓展算法生成32個32 bit輪密鑰。肖-來白盒SM 4做出的改進是在每一輪的加密過程中添加線性編碼，對每一輪的輸入輸出進行混淆，在下一輪的輸入處對上一輪輸出中所添加的混淆進行抵消。白盒SM 4的密鑰被提前確定好，每一輪中與密鑰相關的計算過程以查找表的形式呈現(xiàn)，查找表同時包含了密鑰相關的計算過程以及對輸入輸出的混淆方法。肖-來白盒SM 4一輪的計算過程如圖1所示。

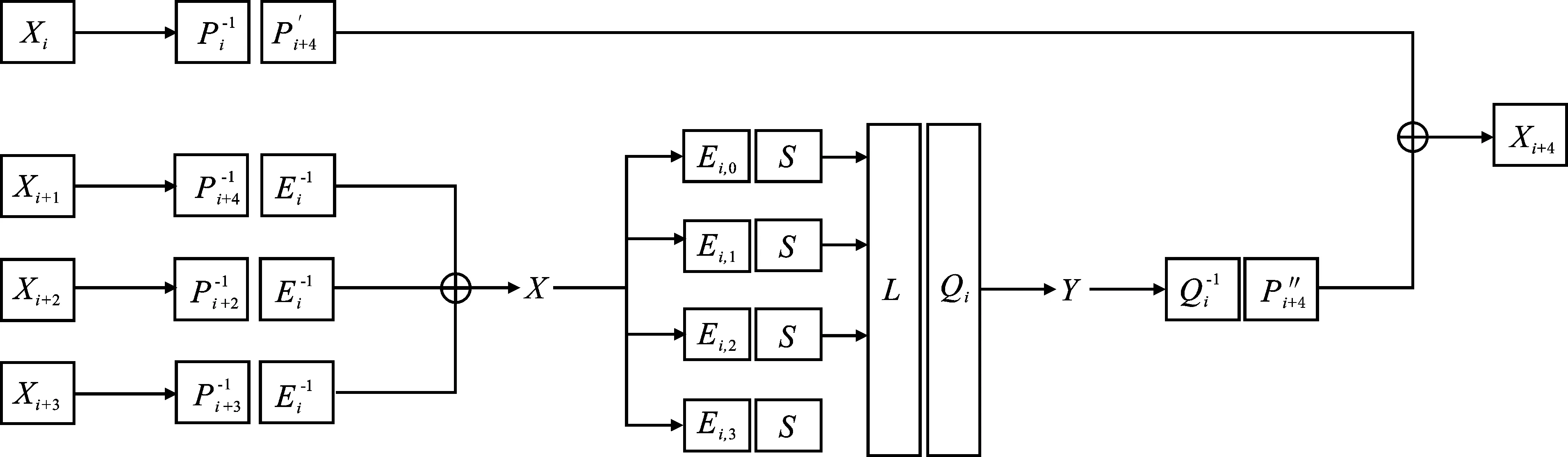
圖1 肖-來白盒SM 4一輪過程

X→Y過程以查找表的形式體現(xiàn)，且密鑰嵌入查找表中，同時考慮到X→Y的變換是32入32出的變換。直接生成查找表會耗費巨大的存儲空間，因此需要進行分割，用4個8入32出的變換以及3個異或操作進行代替，將X=(xi，0，xi，1，xi，2，xi，3)經過Ei，j與S盒及密鑰加操作后的值記為(zi，0，zi，1，zi，2，zi，3)，改進后的第二部分表達式如式(1)。

(Ri，0zi，0)⊕(Ri，1zi，1)⊕(Ri，2zi，2)⊕(Ri，3·zi，3⊕c[Qi]) 。

(1)

l[Qi]與c[Qi]分別表示Qi變換的線性變換與常數(shù)部分，Ri，j(j=0，1，2，3)表示32×8的矩陣。由式(1)可以看出，原來32入32出的查找表被替換成了4個8入32出的查找表以及3個異或操作。一輪加密函數(shù)中的F函數(shù)可以用5個仿射變換、4個查找表、6個異或操作完成。

2 差分計算分析

差分計算分析是灰盒模型下的差分功耗分析在白盒安全模型下的對應軟件版本。該分析使用程序運行過程中的軟件執(zhí)行軌跡來提取密鑰信息，軟件執(zhí)行軌跡包括但不限于程序執(zhí)行期間訪問的內存地址、內存數(shù)據(jù)等變量。差分功耗分析所依據(jù)的原理是執(zhí)行加密操作時所產生的功耗軌跡信息與密鑰密切相關[18]，差分計算分析則認為軟件執(zhí)行軌跡與密鑰同樣密切相關。

差分計算分析可分為以下四步進行。

步驟1 攻擊者首先執(zhí)行一次白盒實現(xiàn)程序，采集其軟件執(zhí)行軌跡，利用可視化工具對其進行處理。

步驟2 攻擊者使用隨機明文獲取軟件執(zhí)行軌跡，每一條明文會對應一個軟件執(zhí)行軌跡。

步驟3 對采集到的軟件執(zhí)行軌跡進行格式化，轉換成適當?shù)母袷剑赃m應接下來的分析。

步驟4 使用差分功耗分析工具對處理后的軟件執(zhí)行軌跡進行分析，提取出密鑰信息。

進行步驟1的主要目的是定位出與密鑰相關的計算部分，以便縮小采集范圍，節(jié)省分析所需的內存空間，在內存空間充足時可跳過該步驟。軟件執(zhí)行軌跡的采集可以利用PIN[19]或者Valgrind[20]等動態(tài)二進制分析軟件以及相關的插件來完成。而對于軟件執(zhí)行軌跡的格式化只是將采集的信息限制到單一的種類中，比如只采集寫入內存的數(shù)據(jù)或只采集從內存中讀出的數(shù)據(jù)。前幾個步驟的目的是對采集到的數(shù)據(jù)進行處理，使其盡可能地適應差分功耗分析，而在分析步驟中只是將差分功耗分析的對象從電路功耗換成了二進制形式的軟件執(zhí)行軌跡，同時由于軟件執(zhí)行軌跡中不會存在噪聲，所以往往分析的結果更加精確。

差分計算分析需要攻擊者能夠在受控環(huán)境下重復多次執(zhí)行二進制白盒實現(xiàn)程序，并且攻擊者掌握白盒實現(xiàn)外部編碼的輸入編碼或者輸出編碼任一部分。這兩點是能夠進行差分計算分析的基本定義，只有滿足以上兩點，才能夠完整地運行差分計算分析的全部步驟。

文獻[5]中的差分計算分析所需要的軟件執(zhí)行軌跡為白盒程序運行時的內存讀寫記錄，采用均值差分對其進行統(tǒng)計分析。文獻[21]在差分計算分析的基礎上提出了差分數(shù)據(jù)分析(Differential Data Analysis，DDA)。該分析與差分計算分析基本類似，不同之處在于需要的軟件執(zhí)行軌跡為加密過程中所有查表結果，利用相關系數(shù)(如皮爾遜相關系數(shù))進行統(tǒng)計分析。差分數(shù)據(jù)分析所需的分析對象為查表結果，該數(shù)據(jù)較差分計算分析所需的內存訪問記錄更易于采集，但差分數(shù)據(jù)分析需要計算數(shù)據(jù)的皮爾遜相關系數(shù)來進行統(tǒng)計分析，該步驟卻比差分計算分析中計算均值差分來進行統(tǒng)計分析的方法更復雜。文獻[5，21]中實驗顯示，差分計算分析所需要的軟件執(zhí)行軌跡數(shù)目通常為數(shù)千條，而差分數(shù)據(jù)分析所需要的軟件執(zhí)行軌跡數(shù)量為數(shù)百條。綜合以上兩種分析的優(yōu)點，采用更易于采集的查表結果為分析對象，并以復雜度更低的計算均值差分作為統(tǒng)計分析的方法，筆者提出了用于白盒SM 4密鑰提取的新型分析方法，名為中間值平均差分分析(Intermediate-Values Mean Difference Analysis，IVMDA)。

3 中間值平均差分分析

介紹中間值平均差分分析，應用該分析對肖-來白盒SM 4進行密鑰提取工作，給出了實際分析結果，并根據(jù)結果對分析做出相應改進。

3.1 攻擊模型與原理說明

中間值平均差分分析的目標是能夠在實際應用環(huán)境下對白盒SM 4進行密鑰提取。傳統(tǒng)的白盒安全模型中，攻擊者對算法的細節(jié)以及運行環(huán)境都具備完全的了解以及控制能力，但在實際應用環(huán)境中的攻擊者往往不具備該攻擊條件。根據(jù)實際應用環(huán)境中白盒實現(xiàn)面臨的現(xiàn)實性威脅對攻擊者的能力進行定義。白盒實現(xiàn)的攻擊者是一個帶有惡意目的的合法用戶，掌握白盒實現(xiàn)的二進制程序，并具備一定的逆向、代碼調試等能力。攻擊者不直接掌握外部編碼，但可以向外部編碼組件發(fā)送明文并獲得編碼后的明文。攻擊者不掌握白盒實現(xiàn)方案的算法細節(jié)，只了解白盒方案的底層算法種類。攻擊者的分析對象是白盒實現(xiàn)的所有查表結果。

中間值平均差分分析也可以認為是一種差分功耗分析在軟件層面的變體分析方式，差分功耗分析是利用加密芯片運行過程中產生的功耗信息與密鑰的相關性來進行統(tǒng)計分析[18]，從而提取出密鑰信息。中間值平均差分分析的分析對象是加密過程中的查表結果，每一個表中都嵌入了密鑰信息，查表結果與密鑰之間必然存在相關性，因此可以利用統(tǒng)計分析的方法對大量樣本進行分析，提取密鑰。中間值平均差分分析基于以上原理進行密鑰的提取工作。

3.2 中間值平均差分分析

中間值平均差分分析整體分為兩部分：數(shù)據(jù)采集部分與數(shù)據(jù)分析部分。

第1部分數(shù)據(jù)采集。用SM 4白盒實現(xiàn)對n條隨機明文{p0，p1，…，pn}進行加密，順序采集加密過程中產生的128個查表結果，以列表的形式組織數(shù)據(jù)，稱該列表為一條中間數(shù)據(jù)流。每一個隨機明文進行加密的過程都對應一條中間數(shù)據(jù)流ti。最終采集到n條明文及其對應的n條中間數(shù)據(jù)流{t0，t1，…，tn}，并以鍵值對的形式將明文與中間數(shù)據(jù)流對應組織起來。其中明文作為鍵，中間數(shù)據(jù)流作為值。

第2部分對采集到的數(shù)據(jù)進行分析。根據(jù)攻擊者的能力，已知白盒實現(xiàn)的底層算法是SM 4，在該算法中與密鑰相關的計算部分是S盒，一輪中有4個并列的S盒計算，選取算法第一輪中包含密鑰加運算的S盒計算作為中間函數(shù)φ(m0，j，rk0，j)。

φ(m0，j，rk0，j)=S(m0，j⊕rk0，j)=e，j∈{0，1，2，3} 。

(2)

式中，rk0，j表示8 bit長的部分輪密鑰，而m0，j表示進入S盒的8 bit長的中間向量m0，中間函數(shù)的計算結果為e。根據(jù)SM 4算法流程，該中間向量m0由平均分為4部分的128 bit的明文的后三部分異或得到，由于掌握外部編碼的輸入編碼部分，因此可以直接使用原明文利用式(3)對中間向量m0進行計算：

m0=pi，1⊕pi，2⊕pi，3。

(3)

采用中間函數(shù)φ，遍歷部分密鑰rk0，j所有可能的值。選取n條明文對應的m0的一部分m0，j計算中間函數(shù)φ(m0，j，rk0，j)的結果，rk0，j∈{0，1}8，共有256種可能值，根據(jù)rk0，j值將中間函數(shù)結果分為256組。對每一組分別進行以下4步的分析。

步驟1 定義一個選擇函數(shù)φ(e)，對組內每一個中間函數(shù)結果e，利用式(4)計算其選擇函數(shù)的結果。

φ(e)=Sn(e)=b∈{0，1}，0≤n≤7 。

(4)

式中，Sn(e)是取中間結果的第n位。每一個中間結果e對應8個選擇函數(shù)結果b；b是一個比特位，取值范圍只有0和1；根據(jù)n的不同，總共得到8個不同的b，用列表將其組織起來，記作B。

每一組的中間結果e都對應一條明文，而一條明文對應一條中間值數(shù)據(jù)流，同時每一個中間結果e也對應一個B。因此，在不同的e所對應的B中選取一個元素b，可以將其與一個中間數(shù)據(jù)流ti對應起來。

步驟2 設定兩個集合A0，A1。當b為0時，將對應的中間數(shù)據(jù)流分入集合A0中，當b為1時，將對應的中間數(shù)據(jù)流分入集合A1中。隨后，利用式(5)和式(6)計算集合A0與集合A1的均值差分。

(5)

(6)

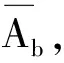
步驟3 對B中所有順序上的元素執(zhí)行步驟2中的分組以及計算均值差分，最終得到8個ΔLC值，選取其中最大的記為Δkey，該值與當前組的密鑰猜測唯一對應。

步驟4 對于所有的假設密鑰值對應的組，執(zhí)行步驟1中計算選擇函數(shù)以及根據(jù)選擇函數(shù)結果進行分組并計算均值差分等步驟。最終得到與當前假設密鑰值惟一對應的Δkey。比較所有的假設密鑰對應的Δkey，Δkey值最大的假設密鑰即為最佳的猜測密鑰。

對一輪中的四個S盒分別執(zhí)行以上分析過程即可完整恢復一輪的輪密鑰。

3.3 實驗結果與分析

采用Python語言實現(xiàn)中間值平均差分分析，對一個肖-來白盒SM 4程序進行密鑰提取。在CPU為Intel(R) Core(TM) i5-6300HQ@2.3 GHz，運行內存大小為8 GB的計算機上執(zhí)行該分析。嵌入白盒實現(xiàn)程序的主密鑰為0123456789abcdeffedcba9876543210(十六進制數(shù)串)，將得到的每一個部分假設密鑰及其所對應的Δkey以圖片的形式展示在圖2中。

第一輪的輪密鑰為0xf12186f9。圖2中表示了第一輪的4部分猜測密鑰值及其對應的Δkey的關系，橫坐標key為猜測密鑰的值，縱坐標為Δkey，根據(jù)中間值平均差分分析的描述，最大的Δkey所對應的橫坐標key為正確的密鑰猜測，并且正確的密鑰猜測對應的Δkey應當為一個明顯的峰值。從圖中結果顯示，并未出現(xiàn)明顯的峰值，波形雜亂無章，同時正確密鑰所對應的Δkey也不是最大值，該結果表明中間值平均差分分析并未成功提取出密鑰信息。重復多次實驗均得到以上結果，結合肖-來SM 4方案對該結果進行分析。

在肖-來白盒SM 4方案中，查找表的輸入、輸出部分存在隨機的仿射對輸入與輸出進行混淆，而輸入的混淆會被抵消，因此只有輸出部分的混淆對查找表的結果產生影響。根據(jù)中間值平均差分分析的原理，查找表的結果與密鑰之間必然存在相關性，而實驗結果卻并沒有反映出該相關性。猜測是輸出部分的混淆影響了實驗結果，設計對照實驗對該猜測進行驗證。

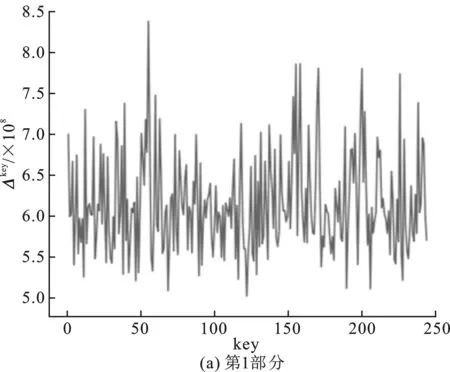
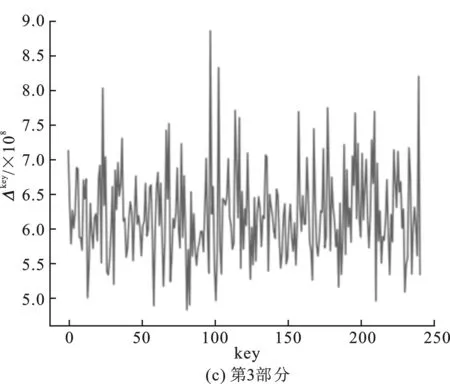
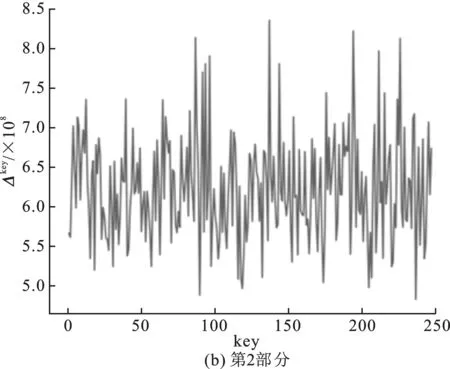
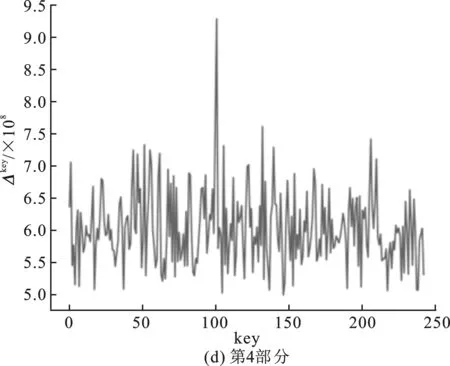
圖2 中間值平均差分分析結果

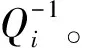
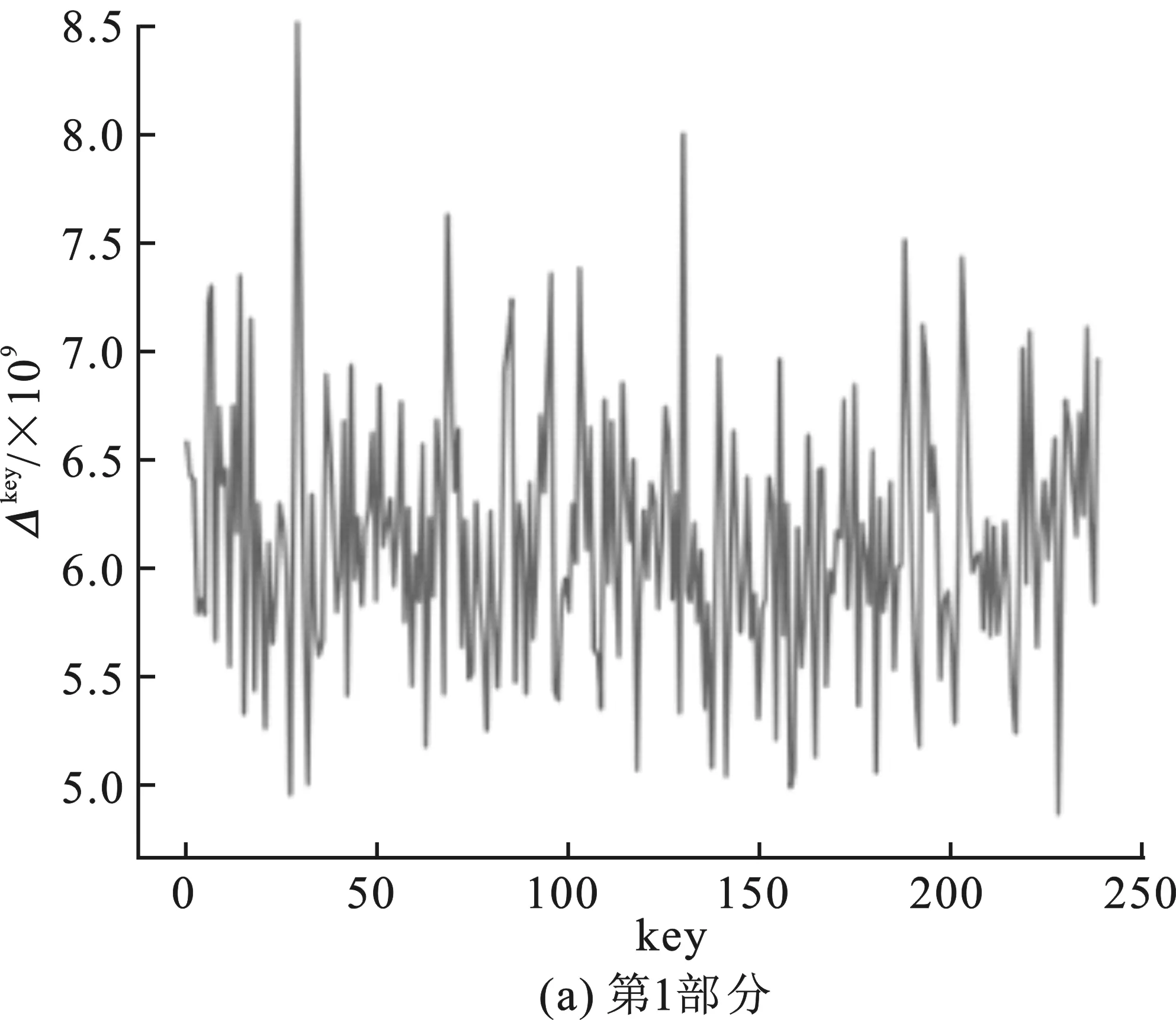
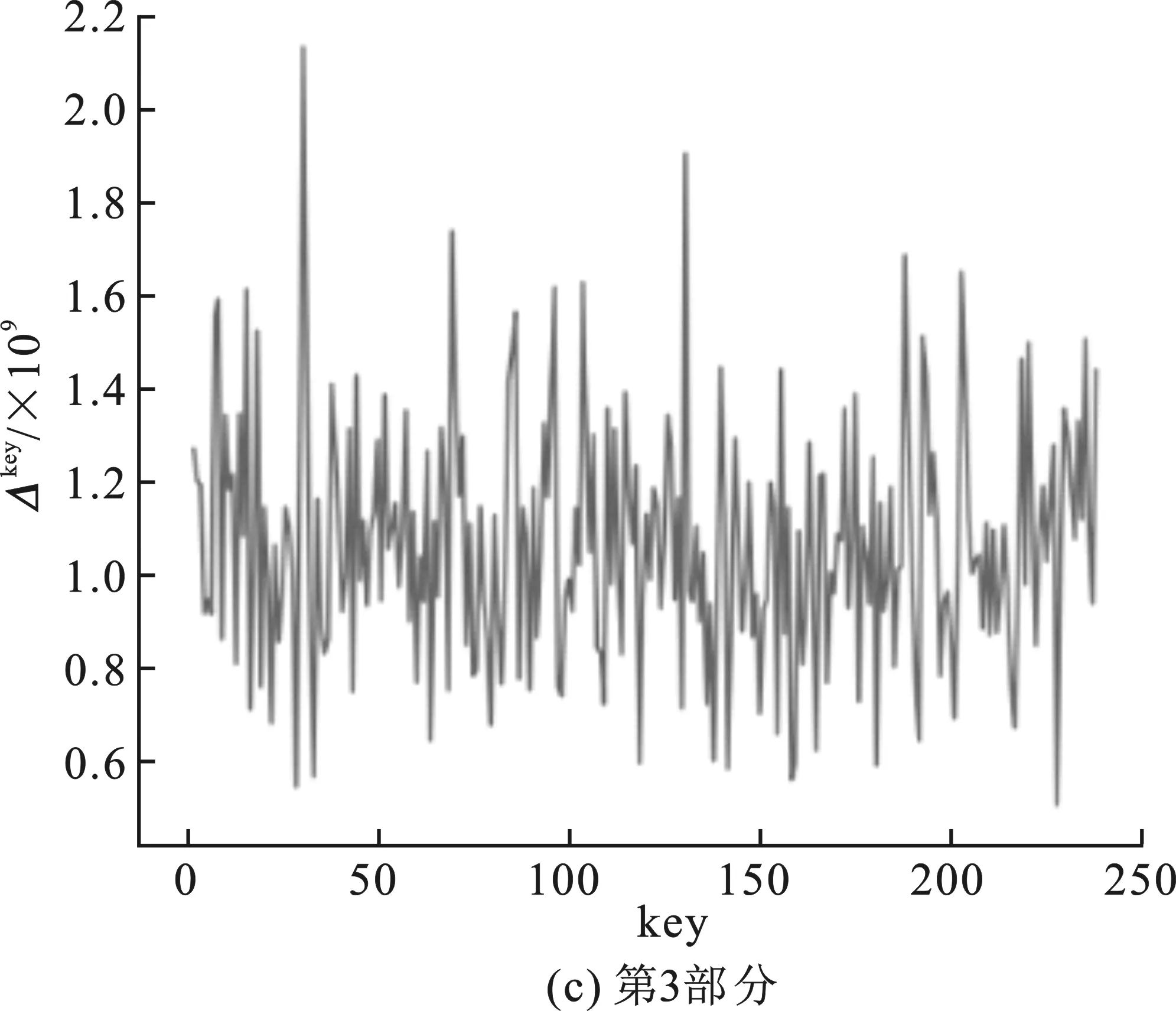
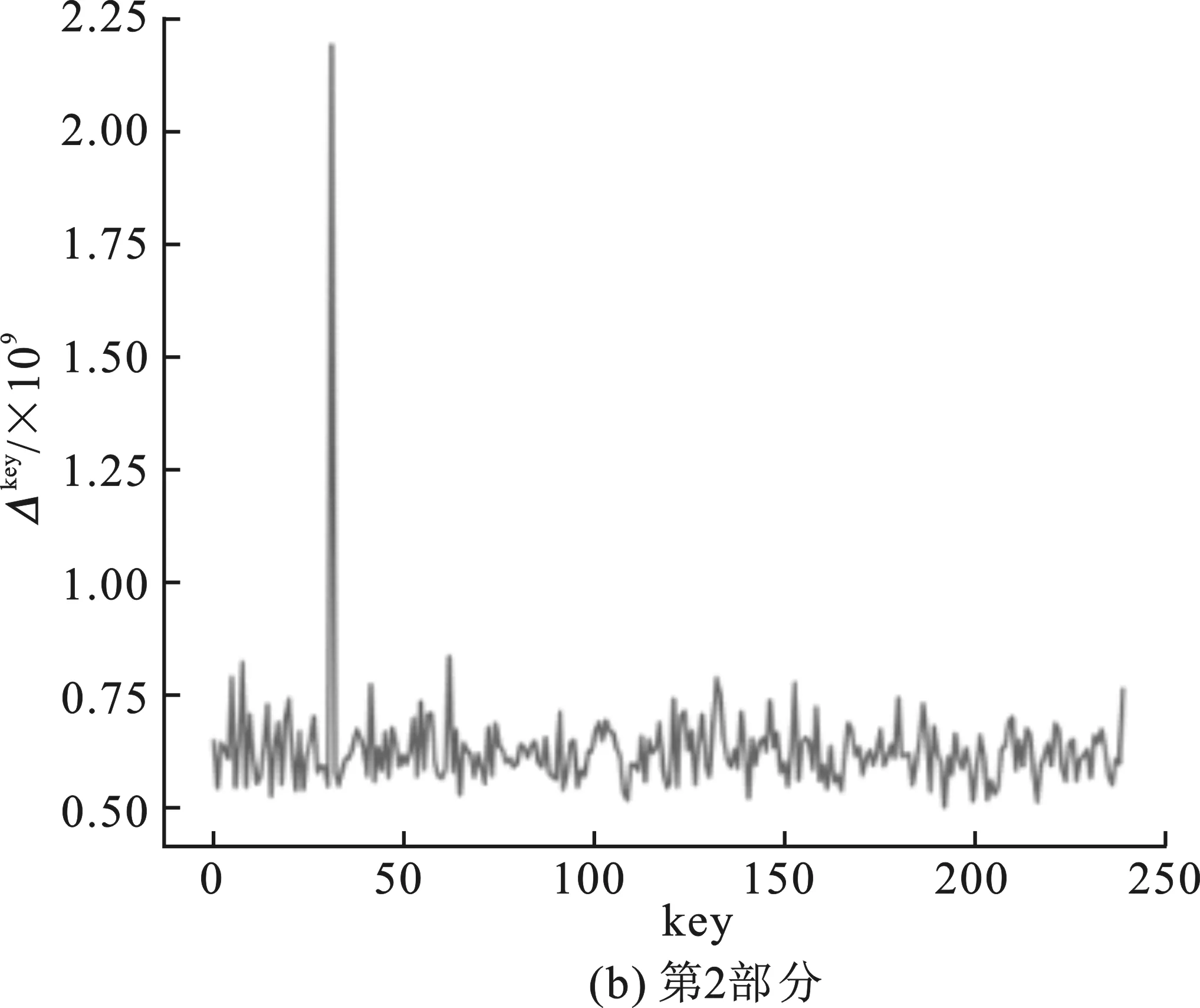
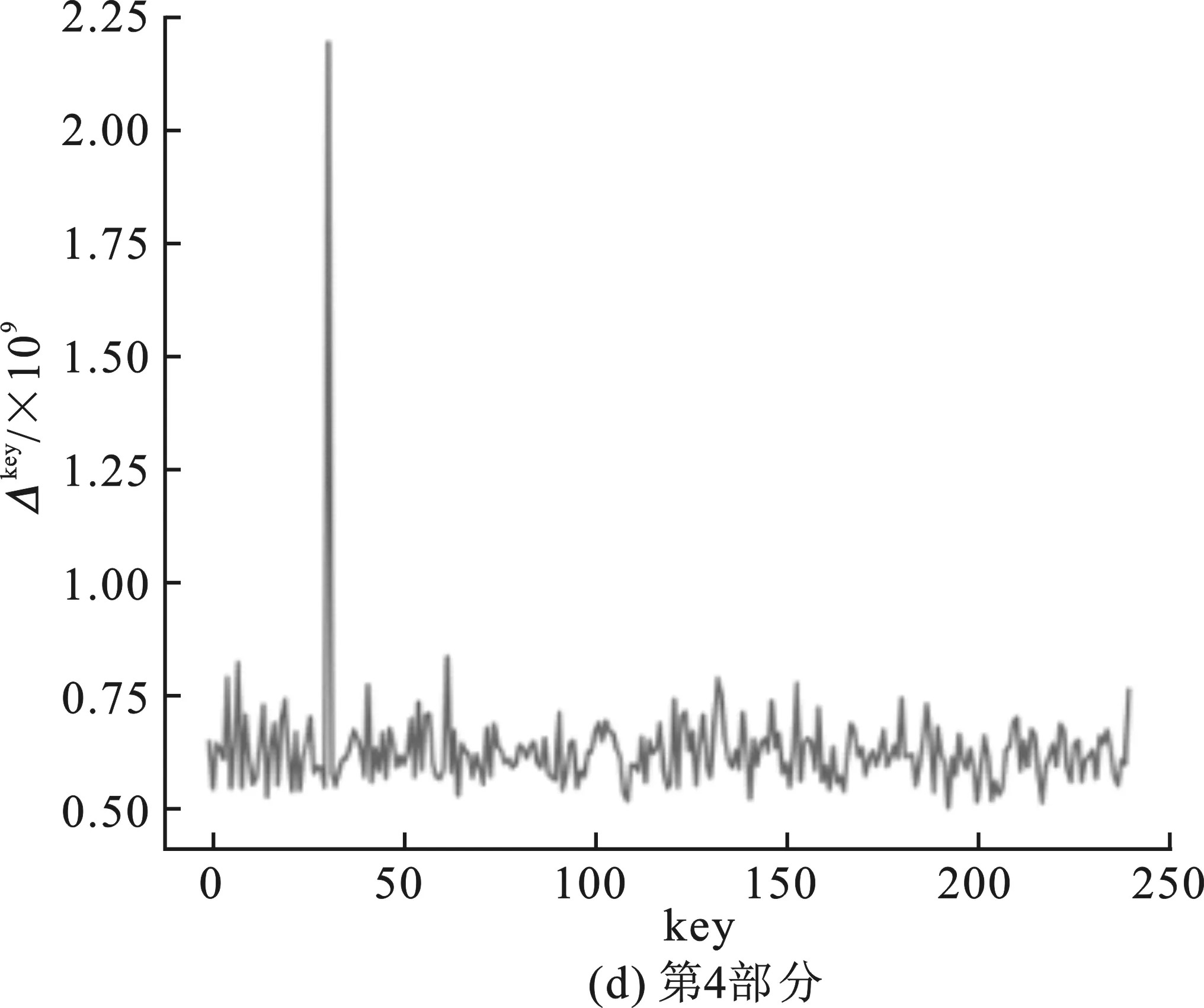
圖3 查找表無輸出編碼的白盒SM 4中間值平均差分分析結果

嵌入查找表主密鑰為0123456789abcdeffedcba9876543210十六進制數(shù)串，第一輪的子密鑰為0xf12186f9。圖3(a)～(d)分別表示對第1輪子密鑰4部分的猜測結果，圖3(a)中最高值對應的橫坐標key為31，十六進制為0x1f；圖3(b)中最高值對應橫坐標key為33，對應十六進制為0x21；圖3(c)中最高值對應橫坐標key為134，十六進制為0x86；圖3(d)中最高值對應橫坐標key為249，十六進制為0xf9。后3部分的分析結果為正確密鑰值，并且正確密鑰對應的Δkey為明顯的峰值。同時改變嵌入密鑰重新生成查找表，進行多次實驗，結果均為后3部分的密鑰猜測值與正確密鑰值相符。

由于可以固定得到第一輪子密鑰的后3部分，因此可以認為在不含輸出編碼的情況下，中間值均值差分分析可以通過對查找表值的分析得出正確密鑰。對比兩次實驗的結果，可以得出結論：肖-來白盒SM 4實現(xiàn)中查找表的輸出編碼部分對中間值平均差分分析造成了干擾，導致分析失敗。

3.4 對中間值平均差分分析的改進

節(jié)3.3的研究與分析表明，查找表輸出編碼是影響分析的關鍵因素。肖-來白盒SM 4實現(xiàn)的混淆手段只有線性編碼，該編碼是對查找表原始輸出進行線性組合得到新的結果，使得假設中間函數(shù)結果與實際查找表結果不匹配。因此，分析步驟中直接利用中間函數(shù)結果進行分組并不能反映密鑰與查表值的關系，需要添加相關操作抵消編碼影響。筆者采用計算中間函數(shù)結果的線性組合的方式來抵消線性編碼的混淆作用。

對于中間值平均差分分析的改進只在選擇函數(shù)的形式上做出了改變，其余部分保持不變。選擇函數(shù)形式如下：

φ(e)=LCe=b∈{0，1}，1≤LC≤255 。

(7)

式中，LC∈{0，1}8取值范圍從1至255，該表達式計算出中間函數(shù)結果的所有線性組合結果，目的是為了消除白盒實現(xiàn)中的線性編碼手段對結果的影響。每一個中間結果e對應255個線性組合結果b；b是一個比特位，取值范圍只有0和1。根據(jù)LC的不同，總共得到255個不同的b，以列表的形式將其組織起來，記作B。

對于一組的中間結果e，每一個都對應一條明文，而一條明文對應一條中間值數(shù)據(jù)流，同時每一個中間結果e也對應一個B。因此，在不同的e所對應的B中選取一個元素b，可以將其與一個中間數(shù)據(jù)流ti對應起來。設定兩個集合A0，A1，當b為0時，將對應的中間數(shù)據(jù)流分入集合A0中，當b為1時，將對應的中間數(shù)據(jù)流分入集合A1中。隨后，計算集合A0與集合A1的均值差分，計算步驟如式(5)和式(6)。對B中所有順序上的元素執(zhí)行以上分組以及計算均值差分的步驟，最終得到255個ΔLC值，選取其中最大的記為Δkey；該值與當前組的密鑰猜測惟一對應。

對于所有的假設密鑰值對應的組，執(zhí)行以上計算選擇函數(shù)以及根據(jù)選擇函數(shù)結果進行分組并計算均值差分等步驟。最終得到與當前假設密鑰值惟一對應的Δkey。比較所有的假設密鑰對應的Δkey，Δkey值最大的假設密鑰即為最佳的猜測密鑰。

3.5 改進后中間值平均差分分析的實驗結果

改進后的中間值平均差分分析采用Python進行實現(xiàn)，對肖-來白盒SM 4的二進制程序進行分析。在CPU為Intel(R) Core(TM) i5-6300HQ@2.3 GHz，運行內存大小為8 GB的計算機上執(zhí)行該分析。嵌入白盒實現(xiàn)程序的主密鑰為0123456789abcdeffedcba9876543210(十六進制數(shù)串)。實驗結果如圖4所示。

根據(jù)主密鑰可計算出第一輪的輪密鑰為0xf12186f9。分析程序對第一輪4部分的密鑰進行猜測，圖4(a)～(b)表示了4部分猜測密鑰值及其對應的Δkey的關系，橫坐標key表示猜測密鑰的值，縱坐標為Δkey。圖4(a)中最高Δkey所對應的橫坐標key為241，轉為十六進制即為0xf1；圖4(b)中最高Δkey所對應的橫坐標key為33，轉換為十六進制即為0x21；圖4(c)中最高Δkey所對應的橫坐標key為134，轉為十六進制為0x86；圖4(d)中最高Δkey對應的橫坐標key為249，轉換為十六進制為0xf9。分析所得結果與第一輪查找表中實際嵌入的輪密鑰完全相符，該分析耗時約為27 min。

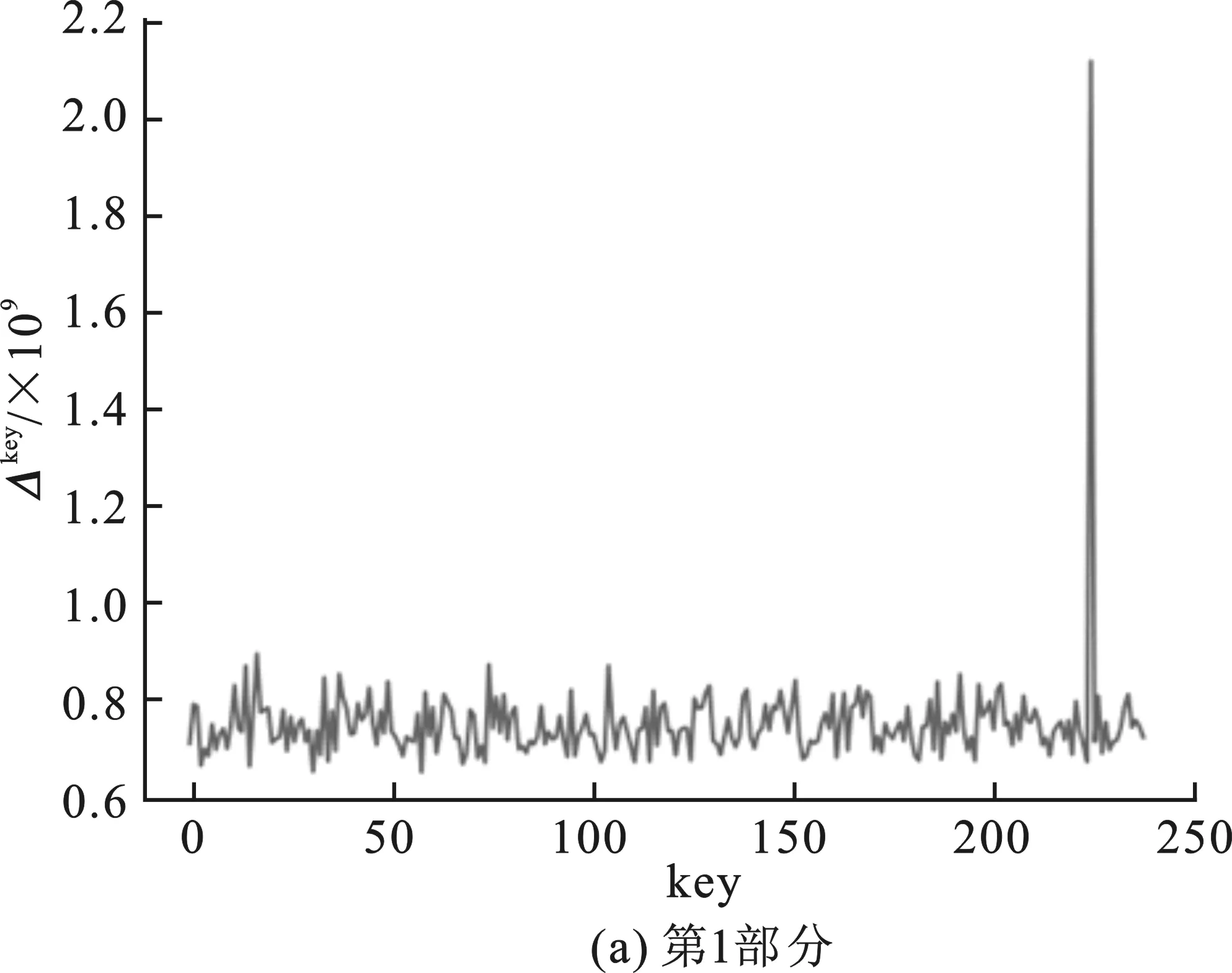
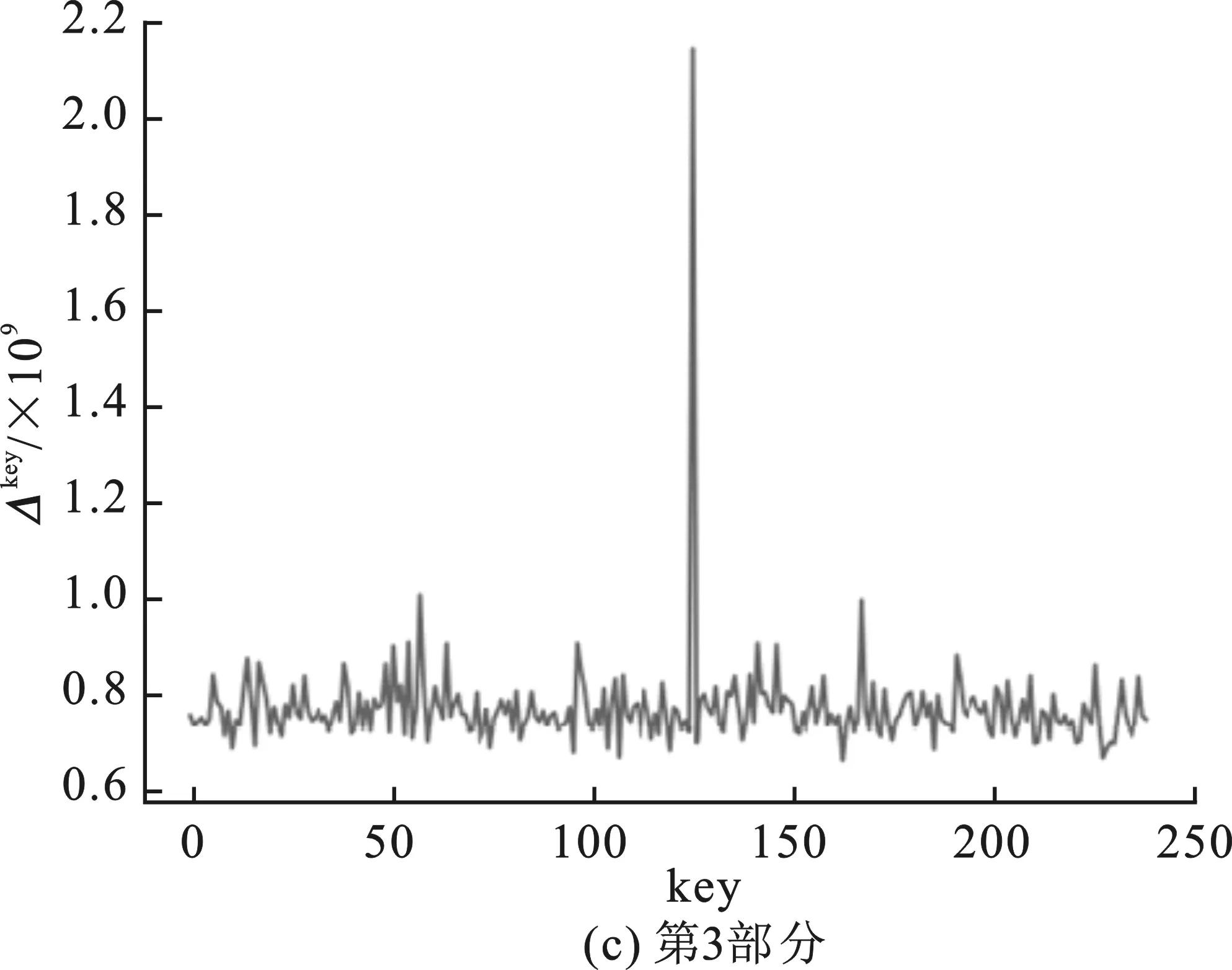
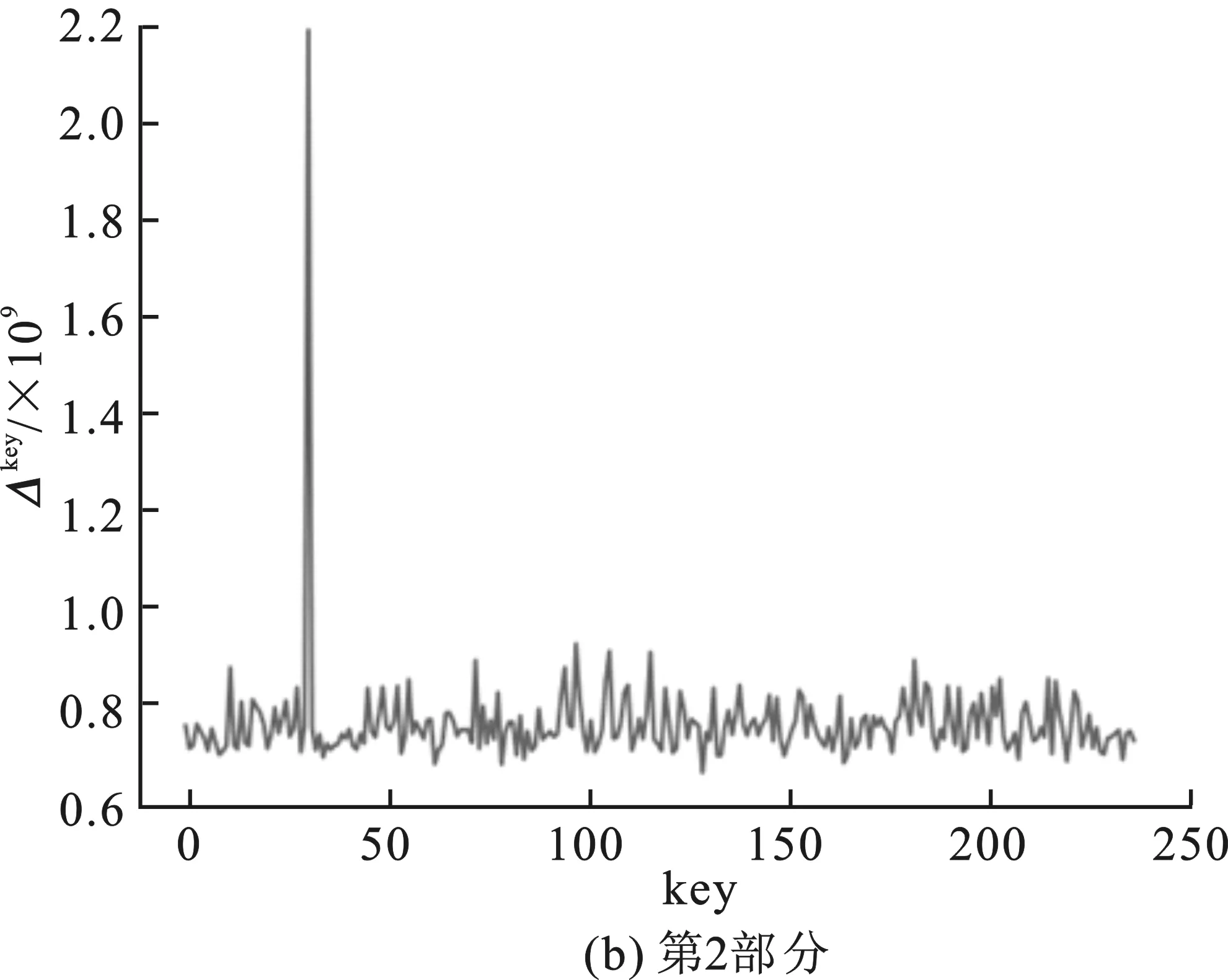
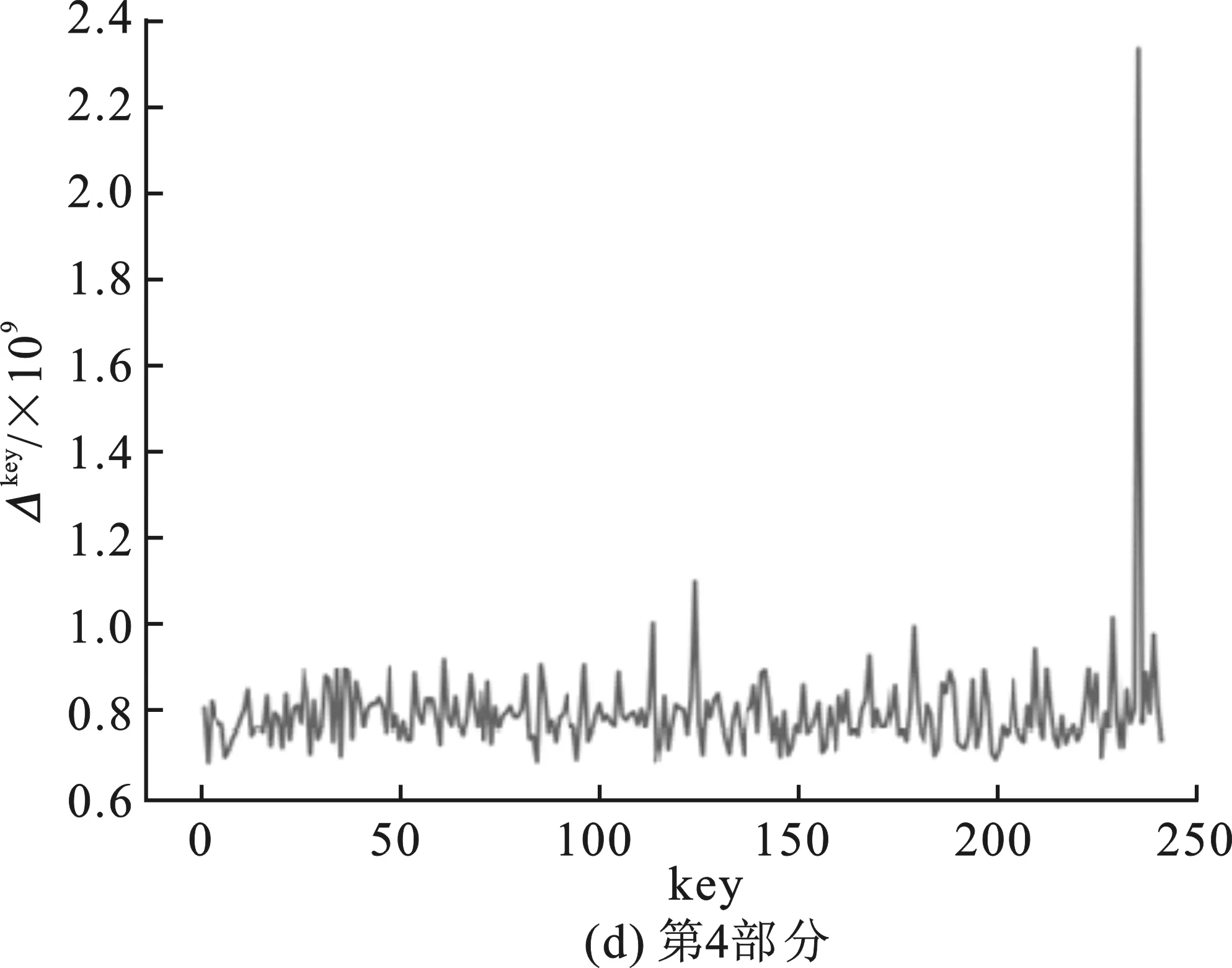
圖4 改進后中間值平均差分分析對肖-來白盒SM 4分析結果

改變參與分析的明文數(shù)量，重復進行實驗。明文數(shù)量與分析結果的對應關系如表1所示。

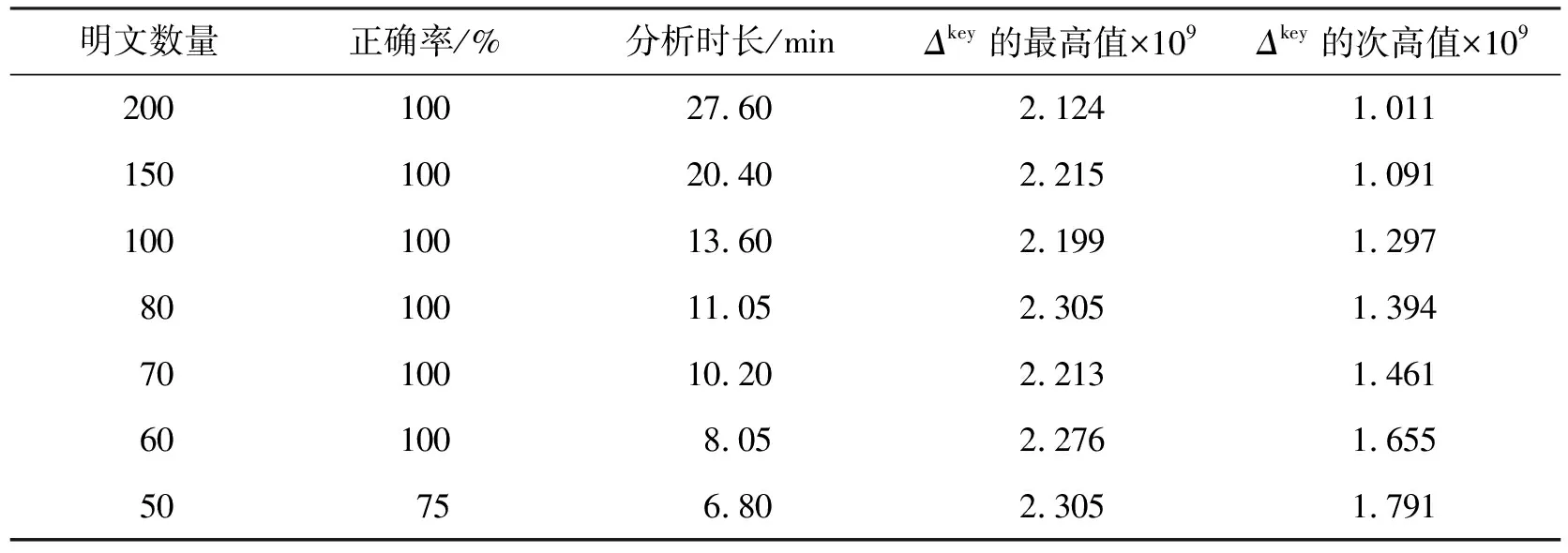
表1 明文數(shù)量與分析結果

從表1的結果可以看出：隨著明文數(shù)目的降低，Δkey的最高值與次高值之間的差距越來越小，在隨機明文的數(shù)量低至一定數(shù)目之后，所得到的分析結果會出現(xiàn)錯誤。實驗結果表明，明文數(shù)量的下限在50左右波動，同時，隨著明文數(shù)量的降低，分析所需時間也會下降，在保證分析正確性的前提下只需要60條明文即可完成密鑰提取工作。

3.6 與其他分析對比

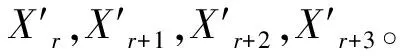
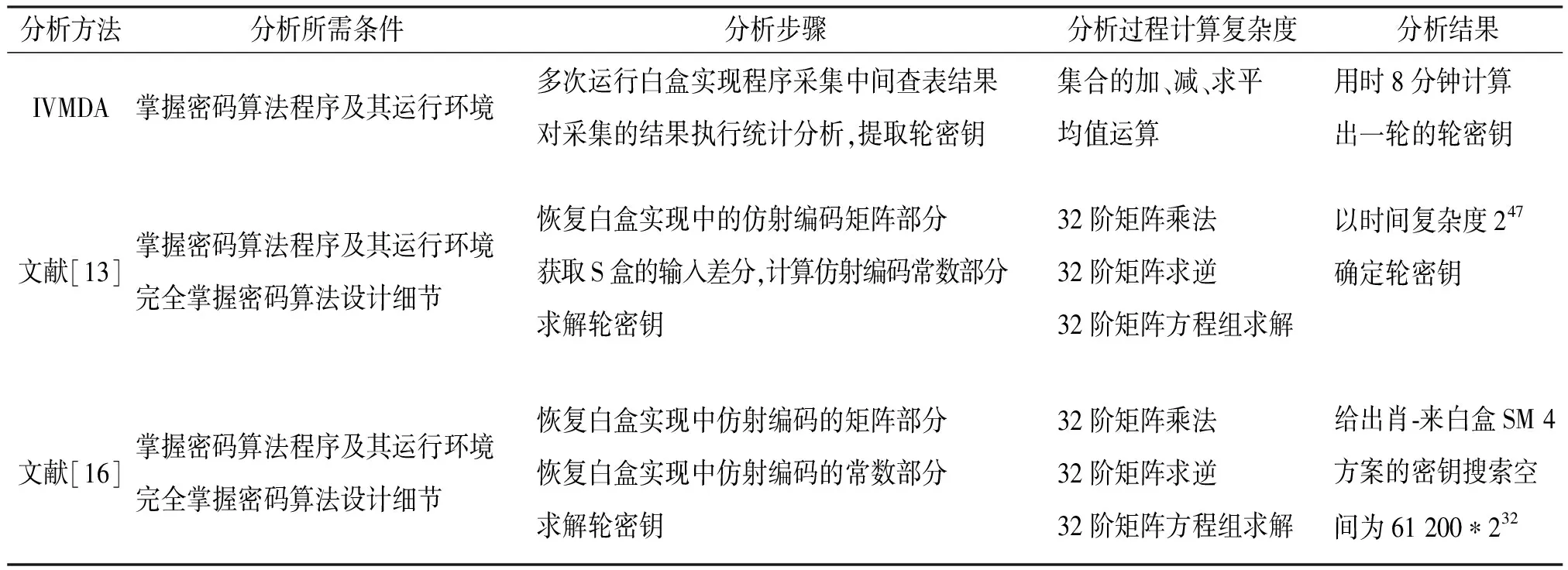
表2 分析方法的對比

通過以上幾方面的對比，可以看出中間值平均差分分析在分析效率、部署簡便性以及分析結果的準確性方面要優(yōu)于潘、林的分析方法。同時，本實驗中的中間值平均差分分析采用解釋型編程語言Python進行實現(xiàn)，其效率還可以通過利用編譯型編程語言重新實現(xiàn)以及引入并行計算等方法進行優(yōu)化，分析的時間還能大幅縮短。

4 總結與展望

筆者在差分計算分析的基礎上提出了中間值平均差分分析。該分析以白盒實現(xiàn)加密過程中的查表結果為分析對象，并且利用線性組合的手段抵消了查找表輸出部分的線性編碼。相比于之前的針對白盒SM 4方案的安全性分析手段，中間值平均差分分析部署簡單、分析效率高、分析結果精確，是一種高效的新型分析方法。為了提高白盒方案的內存效率，近期提出的白盒實現(xiàn)方案均采用線性編碼手段對查找表進行保護，如姚思等人的白盒CLEFIA方案[22]，而中間值平均差分分析的分析對象即為線性編碼保護的查找表。因此，在未來的研究中，可以將中間值平均差分分析推廣到類似的白盒方案的安全性分析工作中來。