巧轉化 習新知 妙解題

廖雨馨

在小學階段的數學學習中，培養學生的數學思維是十分重要的教學目標，而轉化思想又是其中既基本又重要的一種思想，因此教師在日常教學中應注重轉化思想的滲透。本文主要闡述了如何在小學數學教學中滲透轉化思想，有意識地培養學生自覺轉化、有意轉化的習慣，引導學生針對具體問題尋找合適的轉化方法，提高學生從不同角度分析和解決問題的能力，發展數學思維。

轉化是解決數學問題的一種常見的重要的策略，更是數學學習的一種重要的思想方法。轉化的特點是不提倡直接解決問題，而是將問題轉化，即把新問題轉化為舊知識，把一個復雜問題轉化為幾個簡單問題的集合，把抽象問題轉化為具體問題，把特殊問題轉化為一般問題，把逆向問題轉化為順向思維。蘇教版小學數學第十冊第七單元《解決問題的策略》中安排了教學用轉化的策略解決相關的問題，但任何一個新知識，都不可能是憑空出現的，而應當是原有知識發展和升華的結果，直截了當的知識學習、乏味重復的系統訓練遠遠不如潛移默化的學習。且書本篇幅有限，幾個例題習題僅能展現運用轉化思想解決的一部分模式的問題。教師在平時的數學教學中就應當深入發掘教材，合理滲透轉化思想，為此單元的學習奠定堅實基礎，增強利用轉化思想解決問題的策略意識，發展學生形成分析問題、解決問題的能力和數學思考。

一、新知轉化為舊知

學生的學習是不斷汲取新知識的一個過程，而新知又可以轉化為舊知，既是“溫故而知新”又是“教人應使人無被教之感”。教師心中應有一張網，星羅棋布，一脈相通。在實際教學中，教師利用編織的“數學之網”將學生初次接觸的陌生問題沿脈絡轉化成比較熟悉的知識，使學生在熟悉的氛圍中更好地接受新知識，同時也鞏固了舊知識。

例如在三年級圖形與幾何教學中，學生初次通過擺一擺，數一數由小正方形拼成的長方形的面積，探索規律，總結出長方形的面積公式，在學習正方形的面積時，就可以根據舊知“正方形是特殊的、長和寬相等的長方形”，自然而然引出正方形的面積=邊長×邊長;五年級時，學生需要探索平行四邊形的面積公式，教材引導學生動手實踐操作——“剪一剪”“移一移”“拼一拼”，將平行四邊形轉化為長方形，觀察得到平行四邊形的底由長方形的長轉化而來，平行四邊形的高由長方形的寬轉化而來，順其自然得到平行四邊形的面積=底×高;在探索三角形和梯形面積時，學生動手將兩個完全一樣的三角形、梯形拼成一個平行四邊形，發現三角形的底、梯形上下底的和是由平行四邊形的底轉化而來，三角形、梯形的高是由平行四邊形的高轉化而來，這樣的轉化雖提高了難度，但學生因已有之前的經驗，得到三角形的面積=底×高÷2，梯形的面積=（上底+下底）×高÷2輕而易舉;而這樣的鋪墊又能讓學生在之后探索圓的面積時，對于將圓平均分成若干份，拼成一個無限接近長方形的形狀易于接受，通過觀察得到圓的半徑就是由長方形的寬轉化而來，圓周長的一半是長方形的長轉化而來，推算出圓的面積=πr2水到渠成。

而數與代數領域的知識亦可以轉化，加減法的計算是以20以內的加減法為基礎，多位數加減法、小數加減法、分數加減法都是由其計算法則轉化而來的。學生隨著年級升高，認識的數的增大，會將20以內加減法的計算法則延伸至兩三位數的加減法，教師只需稍加引導便可;小數加減法計算法則與整數加減法計算法則中最重要的“滿十進一”一脈相承;分數加減法在學生習得通分之后更是無需教師教學，不少學生已然能熟練計算。乘除法的計算以九九乘法表為基礎，多位數乘除法、小數乘除法都可以轉化為表內乘除法。九九乘法表解決了表內乘除法，兩位數乘一位數結合了表內乘除法的算理與數的組成，多位數乘除法亦是如此，而小數乘除法更是直接建立在多位數乘除法算理之上。不僅僅如此，加法與減法、乘法與除法、加法與乘法之間又存在著相互轉化的關系：一道加法或乘法算式可轉化為兩道減法或除法算式，加數相同的加法算式可轉化為乘法算式。這樣千絲萬縷的關系需要教師在課堂教學前認真分析教材，把握好教材內容的知識結構，深入分析其中蘊含的轉化思想，在課堂上有意識地培養學生利用轉化思想習得新的計算法則，為后續更高層次的計算學習奠定基礎。例如在學到小數乘法第一課《小數乘整數》時，為了使學生滲透“轉化”思想，在以后的學習中能主動聯想到使用“新知識轉化為舊知識”的轉化方法，我設計了如下的新授課部分：

出示書本例題情境圖、條件、問題：“夏天的時候西瓜0.8元/千克，購買3千克西瓜要多少元？”要解決這個問題，可以怎樣列式？

生：總價=單價×數量，我們可以列式0.8×3=2.4。

師：數量關系正確，但這個列式我們之前沒有學習過，其中一個乘數是小數，怎樣計算小數乘整數？誰能聯系已經學過的知識想辦法把它計算出來？

生1：0.8×3可以看成是3個0.8相加，0.8+0.8+0.8=2.4（元）。

生2：0.8元=8角，0.8元×3可以看成8角×3，得數為24角，24角=2.4元。

生3：8×3=24，我猜想0.8×3=2.4。

師：第一位同學根據乘法的意義——“求幾個相同加數的和可以用乘法計算”，將乘法轉化為加法求出答案，第二位同學是利用單位換算——1元=10角，把以元為單位的小數轉化成以角為單位的整數求出來的，其實大家都在不知不覺都把新知識轉化成了舊知識。（板書：新知識→舊知識）

師：把新知識轉化成已經學過的舊知識，這種方法就是轉化的思想方法（板書：轉化）。在今后學習數學時經常要用到這種方法，遇到新問題時認真思考，看是否把它轉化為已經學過的問題進行解決。

通過這樣的設計，使學生領悟到，新知識其實并不新，只要將所學的知識與已學過的知識溝通起來，并運用正確的數學思想方法，就能順利地理解內化為自己的能力。因此在每一次教學的過程中，應當讓學生感受形成過程，及時總結聯系，以構成知識的“網”。

二、復雜轉化為簡單

小學數學階段涉及的等量關系雖千變萬化，根據具體情境總有差異，但不外乎以下四類關系：部總關系、相差關系、倍數關系、總分關系，再復雜的解決問題也不會逃離之外。例如：一只毛毛蟲，一天天慢慢長大，每天的長度是前一天的2倍，20天后長到了40厘米，那么它是第幾天長到10厘米的？根據題意，很多學生能得到等量關系“后一天的長度=前一天的長度×2”。但是題目中并沒有告訴我們毛毛蟲第一天的長度，學生對這種毫無頭緒的問題無法解決，感覺繞進了一個死胡同。但是，如果把這道題目乘法的數量關系轉化為除法“前一天的長度=后一天的長度÷2”，至此學生便豁然開朗，問題變得簡單了，第19天的長度是第20天長度的一半（40÷2=20厘米），第18天的長度是第19天的一半（20÷2=10厘米），通過一一列舉法，就可以得到問題的答案，學生驚喜之余，收獲解題的成就。

轉化的思想方法在解決分數的實際問題時也十分重要，如：“工程隊修一段公路，已修的米數是未修的[13]，如果再修10米，已修的米數是未修的[25]，這段公路長多少米？”雖然兩個分數前面都是“未修的”，但由于在修路的過程中，“已修的”和“未修的”總在發生變化，這便是一道略微復雜的單位“1”不統一的問題。在教學時，我們可以引導學生在碰到此類問題時有意識地先將條件中的單位“1”統一，再解答問題。“已修的米數是未修的[13]”在此條件中，未修的米數是單位“1”，平均分成3份，已修的米數是這樣的1份，而根據“總長度=未修的米數+已修的米數”可知總長度是這樣的4份，因此可將題中條件轉化為“已修的米數是全長的[14]”，而“已修的米數是未修的[25]”以同理思考，將此時未修的米數看作單位“1”平均分成5份，已修的米數是這樣的2份，全長是這樣的7份，題目便可轉化為：“工程隊修一段公路，已修的米數是全長的[14]，如果再修10米，已修的米數是全長的[27]，這段公路長多少米？”將復雜的單位“1”不統一的題目轉化為簡單的單位“1”統一的題目，選擇典型的實際題目，通過為學生提供合適的探索空間，引導學生逐步積累針對具體問題的轉化經驗。學生通過解決這類問題的體驗，不斷反思，當遇到一個難以直接解決的問題，通過深入觀察和研究，轉化為簡單問題便可，在此探索過程中逐步加深了對轉化的認識，提高用轉化策略解決問題的能力。

三、數字轉化為圖形

數字轉化為圖形即數學上常提到的“數形結合”思想，數形結合就是一種將數學語言與圖形相互結合起來的思想，小學生的邏輯思維能力較弱，純粹的數字語言難以理解，而使用數形結合思想則可以引導學生開拓一種新的轉化方法，借助形的直觀來闡述數之間的關系，可以使復雜問題簡單化，抽象問題具體化，從而實現提高學習效率的目的，亦為初中數學的學習奠定基礎。例如：在教學運算律之乘法分配律（a+b）×c=a×c+b×c時，為了使學生能更好地理解記憶乘法分配律，我設計了如下的環節：

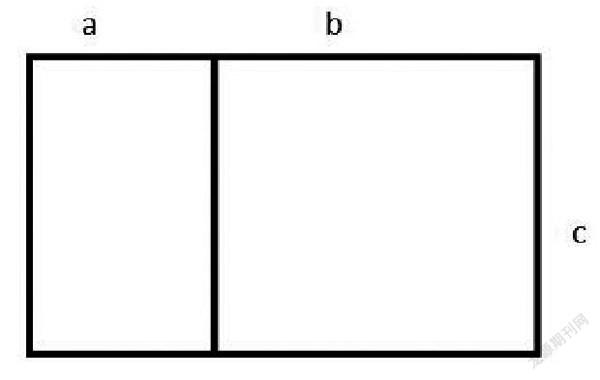
師：請大家求出圖中最大的長方形的面積。

生1：這是一個長是（a+b），寬是c的大長方形，面積可以用這樣的字母表達式表示：S=（a+b）×c。

生2：這是由兩個小長方形組合而成的大長方形，左邊的長方形長c，寬a，面積為a×c，右邊的長方形長b，寬c，面積為b×c，最大的長方形的面積S=a×c+b×c。

師：同學們真棒！說的都非常對，居然用了兩種不一樣的方法來求這個最大的長方形的面積。這兩種方法殊途同歸，表示的都是這個大長方體的面積，因此，我們可以為這兩個式子畫上等于號，變為（a+b）×c=a×c+b×c。

通過解決實際問題引入，再通過自行列舉大量算式總結出乘法分配律，這種方法對于四年級的學生而言略顯枯燥，歸納總結難度也較大，而通過圖形既直觀又能自然而然引出字母表達式。

四、數學轉化為生活

《數學課程標準》明確指出：“數學教學要緊密聯系學生的生活情境，從學生的生活經驗和知識出發，使學生初步感受數學與日常生活的密切聯系。”“數學學習的內容應當是現實的、有意義的、富有挑戰的。”數學知識若直接呈現給學生，必是抽象、理性與標準的數學模型，小學生的認知水平有限，對于數學的很多未知領域探索能力較差。因此，在小學數學中，把抽象的知識還原到生活中，生活化的課堂情境更能激起學生學習的興趣，發掘數學與生活的聯系，主動在生活中探索數學問題。例如：在教學《平均數》一課時，我設計了如下的教學活動：將學生分為四人一組，計算每個小組的平均身高。相較于書本上的習題，來源于生活的活動使得學生的積極性立馬被調動起來，課堂氣氛十分活躍。在每組求出結果后，不僅僅讓完成速度較快的小組交流經驗，更拋出一系列的問題：“你是用什么方法來計算你們小組的平均身高的？”“通過這些數據，你能得到什么結論？”。平均數的相關知識點——求平均數的方法、平均數的范圍……其實都蘊含在學生的頭腦風暴中。這樣的教學活動使得學生意識到數學與生活之間的緊密聯系，不能脫離生活學習數學，激發學生學習數學的興趣。同時，在這樣的課堂活動中會出現各種現實的問題，學生更有興趣去解決，其中蘊含的數學知識，學生更容易掌握理解并牢記在心。數學不僅反映生活更需要服務于生活，數學知識最終應當用于解決生活中的問題，數學轉化為生活，學生更善于用數學的眼光觀察生活中的問題，真正體會到數學知識的價值。

總而言之，轉化思想是數學思想的精髓，數學中許多知識可以用到轉化，可用轉化策略分析和解決的實際問題有很多，卻沒有統一的固定的模式。作為教師，我們應當全面了解學生，深入研究他們的知識水平，努力鉆研，將數學轉化思想貫穿于小學數學教育的始終，通過逐步積累用轉化策略解決問題的經驗，增強學生主動運用策略的自覺性，如順水推舟般提高學生的數學素養，促進學生能力的全面發展，為學生的持續發展奠定堅實的基礎。