有限維Hilbert空間中一類框架與緊框架的構造
江岸, 朱玉燦
(福州大學數學與統計學院,福建 福州 350108)
0 引言
框架是Hilbert空間中標準正交基的推廣. 其與標準正交基的區別在于, 對于一個具體向量, 用框架表示出該向量的方式可能有無窮多種. 在信號傳輸中, 經常會有傳輸信號遭到丟失, 而重新傳輸會帶來過大延遲而不可接受. 為此, 需要設計一個專業編碼方式, 以使得接收端能從不完整的傳輸結果部分或完全恢復原始信號. 因此, 研究者尋求將信號建模成向量, 并通過框架編碼、傳輸、解碼這種做法, 以令信號具備相對于丟失的恢復能力[1]. 近年來研究者從編碼學的角度研究框架性質[2-4], 以求找到編碼、傳輸以及解碼領域上的最佳框架. 與一般框架相比, 緊框架由于在框架重構時容易計算框架算子的逆算子, 在許多實際問題, 諸如信號處理中有非常重要的應用, 因此越來越多的人重視對緊框架的研究.
Parseval框架是一種特殊的緊框架, 其框架算子為恒等算子.N維Hilbert空間HN的各種Parseval框架中, 有一類被稱為幾何等模框架的框架可以通過將構成循環交換群的算子迭代作用到單個向量生成[5], 這些框架可按酉等價性分類, 每類可選一個調和框架作為代表元. 調和框架由于其特殊性質被廣泛研究[4]. 有限維空間中的框架或者緊框架的具體構造是框架理論在實際問題中應用的一個關鍵環節, 因此有限維空間中的框架或者緊框架的具體構造是一個研究的熱點. 文獻[4] 中提出了四種緊框架構造方法, 其中有些相當復雜. 文獻[6]從一個序列延拓成緊框架, 文獻[6-9]利用 Tetris 譜塊來構造框架或者緊框架. 文獻[10]提出了用Hadamard矩陣構造緊框架的方法, 而文獻[11]提出了用奇異值分解構造酉矩陣的方法等.
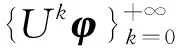
1 預備知識
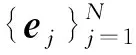
下面將介紹有限維的框架、調和框架與一般調和框架的相關基本概念, 并引入準調和序列及準調和框架.由于一般的N維復Hilbert空間HN等距同構于CN[13], 討論集中于空間CN.
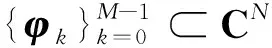
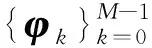
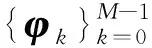
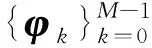
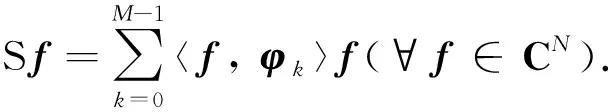
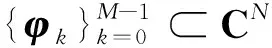
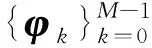
定義4[14]稱算子U∈B(CN)為酉算子, 若U*=U-1在CN中可以定義調和框架, 及其推廣一般調和框架.
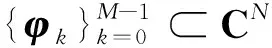
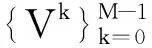
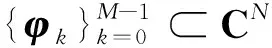
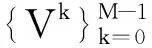
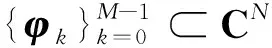
可以看到, 調和框架、 一般調和框架和一般準調和序列在通過生成的方式上具有十分類似的形式, 這使得繼續推廣得到以下的正規迭代式序列的概念.
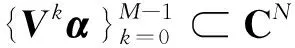
則其分析算子T在自然標準正交基下的矩陣表示為
合成算子T*在自然標準正交基下的矩陣表示
框架算子S在自然標準正交基下的矩陣表示為
2 主要結論及其證明
2.1 正規迭代式框架的構造方式
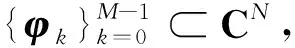
按照前述引言中的內容, 已得每個一般準調和序列都是正規迭代式序列.下面將利用Vandermonde行列式, 得到正規迭代式框架的生成矩陣刻畫.
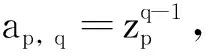
為了得到主要結果, 先給出幾個引理:
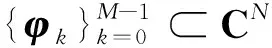
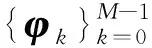
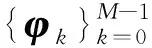
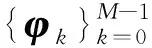
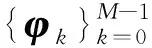
引理3[15]設A為CN中的N階矩陣, 以下條件等價:
Ⅰ)A是正規的, 即A*A=AA*;
Ⅱ)A可酉對角化, 即存在N階酉矩陣U使得:A=Udiag(λ1,λ2, …,λN)U-1.這里,λ1,λ2, …,λN為A的特征值;
Ⅲ)A有N個彼此正交的特征向量.
引理4給定C中的N階矩陣V是正規的, 設其特征值為λ1,λ2, …,λN, 則存在一組分別與這些特征值對應的單位的特征向量v1,v2, …,vN, 彼此正交.稱這些向量為V的一組特征標準正交基.令矩陣U=(v1,v2, …,vN), 則U為酉矩陣, 且V=Udiag(λ1,λ2, …,λN)U-1.
證明 由于V是正規的, 由引理3得V存在N個彼此正交的特征向量, 從而存在彼此正交的單位特征向量v1,v2, …,vN分別與特征值λ1,λ2,…,λN對應.
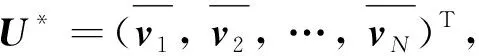
由于v1,v2, …,vN彼此正交, 且均為單位向量, 有p=q時 〈vq,vp〉=1, 而p≠q時〈vq,vp〉=0.故而U*U=I, 所以U為酉矩陣.由于v1,v2, …,vN為V的特征值λ1,λ2, …,λN所分別對應的特征向量, 可得:
所以V=Udiag(λ1,λ2, …,λN)U-1.
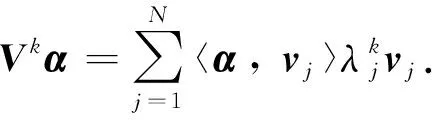
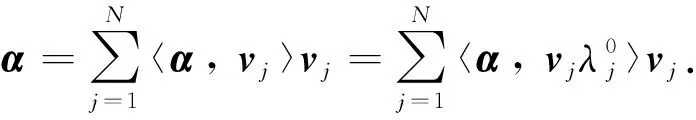
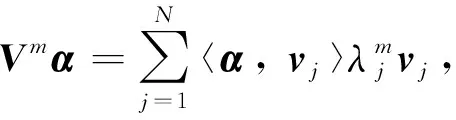
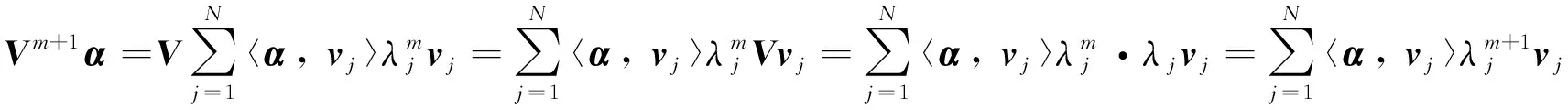
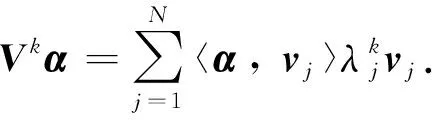
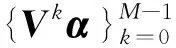
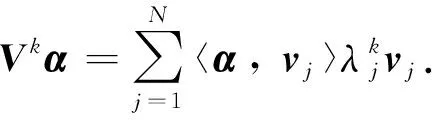

(1)
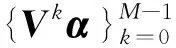
令矩陣

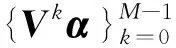
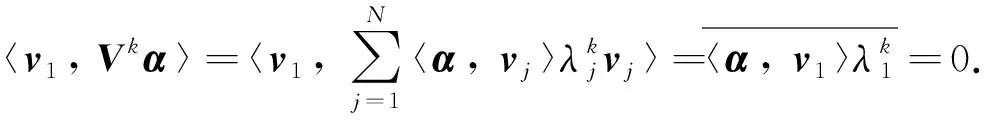
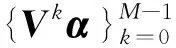
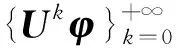
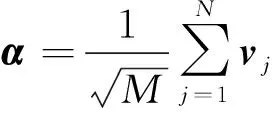
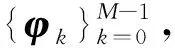
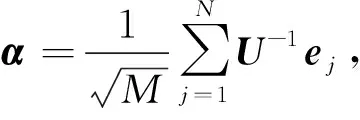
2.2 正規迭代式的緊框架的構造方式
由于一般調和框架均為等模Parseval框架, 而作為其推廣的一般準調和框架, 以及更一般的正規迭代式框架均為等模序列, 所以本研究考慮符合哪些條件的正規迭代式框架能成為緊框架乃至Parseval框架. 下面的結論說明除了在空間維數N為 2的特殊情況, 正規迭代式框架為Parseval框架當且僅當其為一般調和框架.
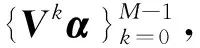
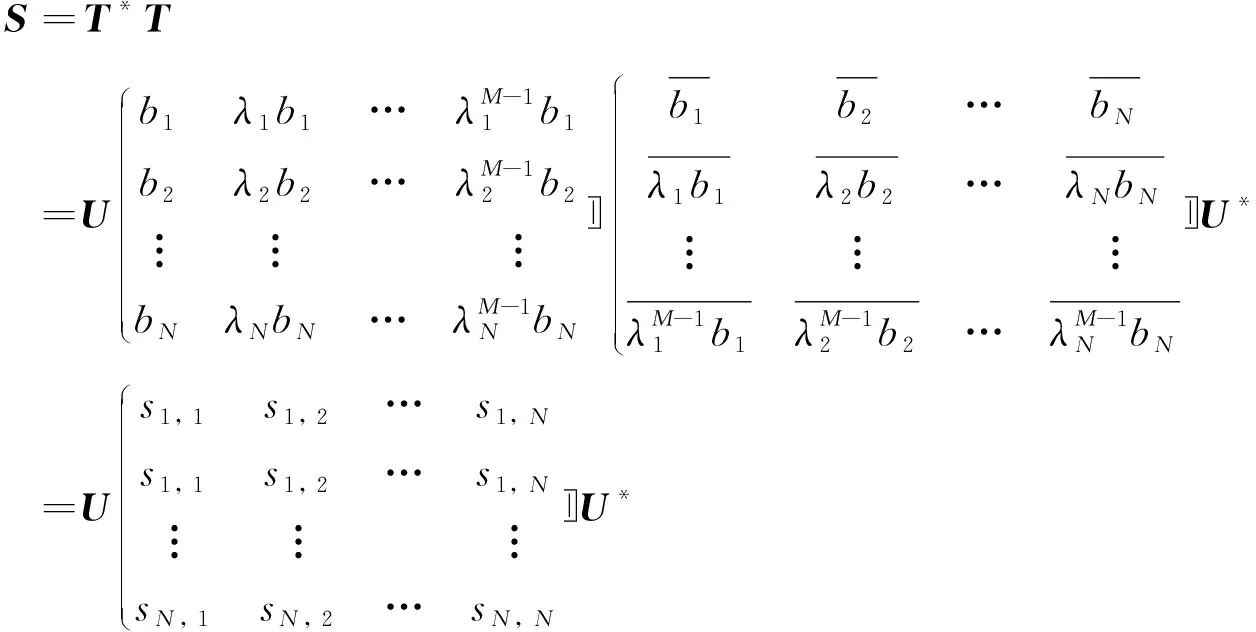
(3)
其中:
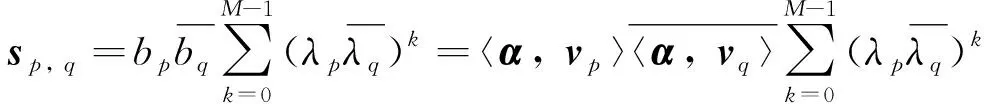
(4)
從而可以得到正規迭代式的緊框架的等價刻畫.
定理2設α∈CN為非零向量,V為C上的N階非零矩陣, 且V是正規的.當M≥N≥3或V為N階酉矩陣時, 以下條件等價:
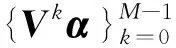
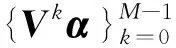
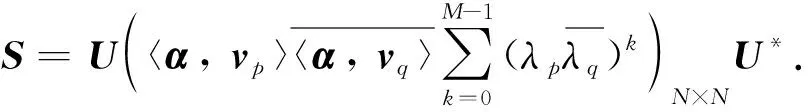
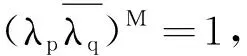
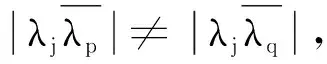
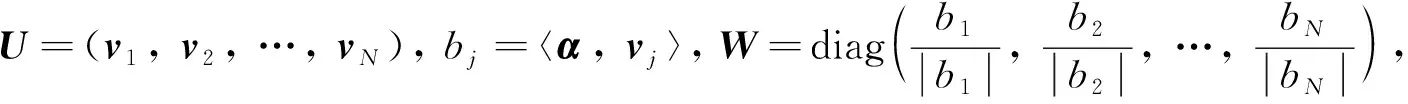
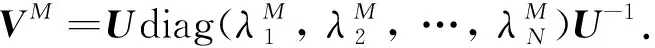
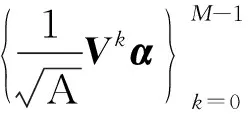
注2在定理2中取A=1時, 用另一種方式得到了文獻[2]中的定理4.1, 從而可以說明本研究的定理2對文獻[2]的結論進行了推廣.
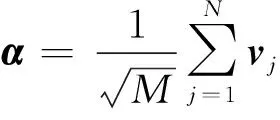
推論2CN的一般準調和序列為緊框架當且僅當其為一般調和框架, 此時亦為Parseval框架.
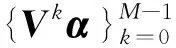
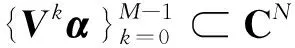
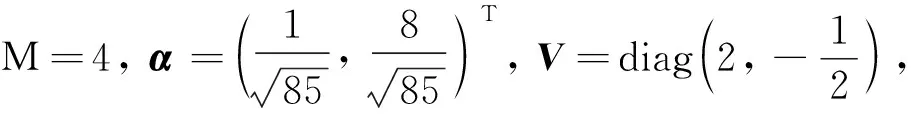
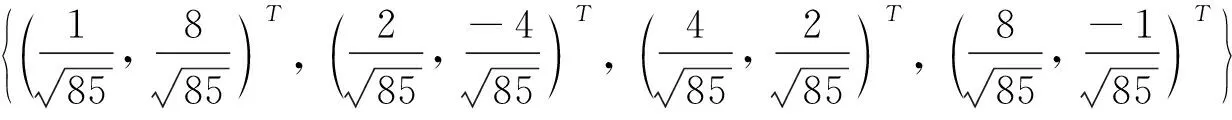
經過計算可得其框架算子S=I, 則該序列為CN的Parseval框架.但該框架不是等模框架, 從而不是一般調和框架.

