采用GRU-MC混合算法的鋰離子電池RUL預測

姚遠，陳志聰，吳麗君，程樹英，林培杰

(福州大學物理與信息工程學院，微納器件與太陽能電池研究所，福建 福州 350108)

0 引言

鋰離子電池的剩余使用壽命(remaining useful life, RUL)是指從當前時刻到電池的壽命終止狀態(EOL)時的充放電循環周期次數[1]. EOL一般是指電池容量下降到其標稱容量的70%～80%時的狀態. RUL的準確預測能夠確保及時更換電池以及電池管理系統的可靠運行. 由于鋰離子電池復雜的化學特性[2]，其容量會隨著電池的連續使用而變化，并且受溫度、電壓、放電倍率等多種因素的影響較大. 因此，RUL的準確預測依然是研究的重點與難點. 目前最常用的是基于等效電路模型和基于數據驅動的兩種預測方法[3].

基于等效電路模型的方法一般是將等效電路物理模型與自適應濾波方法(例如粒子濾波算法(PF)、卡爾曼濾波算法(KF)等)結合起來，根據電池特性搭建等效電路仿真模型，然后使用濾波方法進行RUL預測[4]. 文獻[5]采用粒子濾波器和蒙特卡羅算法結合來預測貝葉斯框架中的電池RUL； 文獻[6]提出了一種高斯-赫姆特粒子濾波方法來預測電池容量的衰減，以進行電池RUL預測. 盡管基于模型的方法具有參數變量較少、可實現性強的優點，但是搭建的仿真模型不能夠完全描述電池復雜的動態特性，當電池參數發生變化時，模型也需要進行相應的調整，不具有泛化性[7-8]. 基于數據驅動的方法不需要明確的數學模型來描述電池的容量退化，僅僅依賴于電池歷史退化數據，可以有效地避免基于等效電路模型方法的不足[9]. 一些常用的機器學習方法，如支持向量機(SVM)、極限學習機(ELM)、高斯過程回歸(GPR)、隱形馬爾可夫(HMM)等[10-13]，已被用于RUL預測. 雖然機器學習方法訓練較快、簡單易實現，但是對于電池RUL這類復雜非線性問題，長期預測的精度會變差. 除上述機器學習方法外，深度學習算法已被用于預測領域. 深度學習方法學習和適應能力較強，尤其是循環神經網絡(RNN)系列算法，適用于具有序列特性的數據的預測(如鋰離子電池RUL的預測)，因此許多專家學者進行了相關的研究分析. 文獻[14]采用基于RNN的鋰離子電池建模方法； 文獻[11]使用長短期記憶網絡(LSTM)依據鋰離子電池數據預測RUL，從而避免了長期RNN導致的梯度消失問題. 文獻[15]使用LSTM-RNN混合算法預測鋰離子電池的RUL. 但是在RNN和LSTM中，當電池數據嘈雜或數據量較小時，通常會發生擬合不足現象. 而最新提出的門控制循環單元網絡(gated recurrent unit, GRU)被認為是LSTM的變體，相對于LSTM少了一個門函數，因此模型參數較少，訓練速度更快，能夠更快收斂. 但是單一的GRU算法可能對多種電池RUL的預測泛化性較差.

為克服上述方法的局限性，本文提出一種基于GRU-MC混合算法的鋰離子電池RUL預測方法，首先對數據進行預處理，構造特征矩陣，利用GRU較優的記憶性，搭建模型對電池RUL進行預測，為了進一步提高預測精度，采用馬爾科夫算法(MC)方法對初步預測結果進行誤差修正，得到最終的電池RUL預測結果.

1 基于GRU-MC混合算法的RUL預測模型

1.1 門控循環單元網絡

門控制循環單元網絡(GRU)是循環神經網絡算法之一. GRU在簡單循環神經網絡的基礎上對網絡的結構做了調整，加入了門控機制，用來控制神經網絡中信息的傳遞. 門控機制可以用來控制記憶單元中的信息有多少需要保留，有多少需要丟棄，新的狀態信息又有多少需要保存到記憶單元中等. 這使得GRU可以學習跨度相對較長的依賴關系，而不會出現梯度消失和梯度爆炸的問題. 而鋰離子電池的RUL就是與之前的狀態具有較強的依賴關系，而且數據量較小，GRU能夠很好地從電池之前的狀態中訓練學習，保留有用的信息，從而得到準確的預測結果. 因此，本研究選擇GRU算法來搭建預測模型.

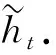
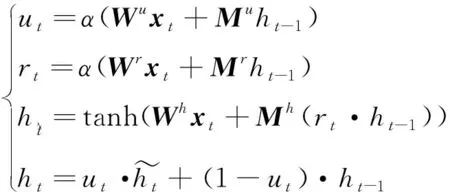
(1)

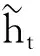
1.2 馬爾科夫鏈

馬爾科夫鏈(MC)是一種數學過程，其利用隨機過程理論對事件的發展規律和可能的預測結果進行狀態劃分，通過研究不同狀態間的轉換規律，從而對預測結果進行修正，提高預測準確率. 單一的預測模型可能對多個數據集的泛化性較低，對預測結果進行誤差修正是一種提高預測精度和泛化性較好的方法. 因此選擇采用MC方法對初始的預測結果進行誤差修正，其具體實現步驟如下：

步驟1. 根據下式，計算初始預測結果的相對誤差，以此進行狀態區間劃分，指定區間上下限：

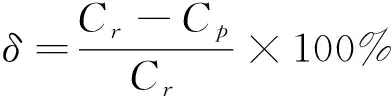
(2)

其中：δ是電池容量預測的相對誤差；Cr是電池容量的實際值；Cp是預測值.

步驟2.通過對每個預測值進行狀態標記，根據相鄰兩個預測值所處的狀態轉換規律，統計得到每個狀態的轉移概率，以此確定狀態轉移矩陣PN：

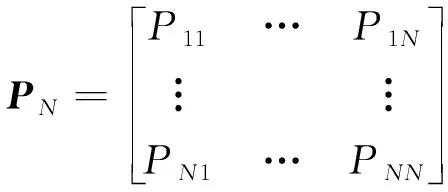
(3)

其中：N表示狀態區間個數，Pij(其中i,j∈[1,N])表示電池容量預測值從劃分的狀態Ei轉移到狀態Ej的概率.

圖2 混合模型預測流程Fig.2 Mixed model forecasting process

步驟3. 根據計算得到的狀態轉移矩陣，求解得到下一時刻預測值的誤差狀態區間，預測結果修正公式如下式所示：

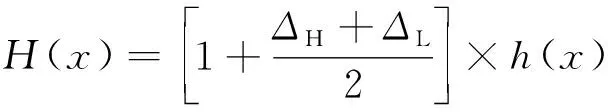
(4)

其中：H(x)表示進行修正后的電池容量預測值；ΔH、ΔL表示所處的誤差狀態區間的上下限；h(x)表示初始的電池容量預測值.

1.3 GRU-MC混合預測模型

混合模型預測流程如圖2所示. 首先，對公共數據集進行數據處理，根據相關性分析提取特征參數，構造特征矩陣，利用GRU保留特征、參數少的優點，搭建了基于GRU的預測模型并進行訓練預測. 根據得到的預測值用MC方法對預測誤差進行修正，確定狀態轉移矩陣并得到預測值所處的誤差狀態區間，通過計算得到最終的鋰離子電池RUL預測量.

2 實驗驗證與分析

2.1 數據集預處理

根據上述提出的模型，采用來自NASA的B0006數據集和CALCE的CS2-33數據集來驗證所提出RUL預測方法的準確性和泛化性. B0006數據集所用的是18650電池，額定容量為2 A·h； CS2-33數據集所用的是CS2電池，額定容量為1.1 A·h. 通過對數據集進行數據清洗和數據規范，將一次完整的充電和放電作為一個周期，兩個電池按周期進行充放電，周期總數分別為168和765，兩個數據集的電池容量變化曲線如圖3～4所示. 選擇采用皮爾遜相關系數法對選取的輸入特征與電池容量進行相關性分析，結果如表1所示.

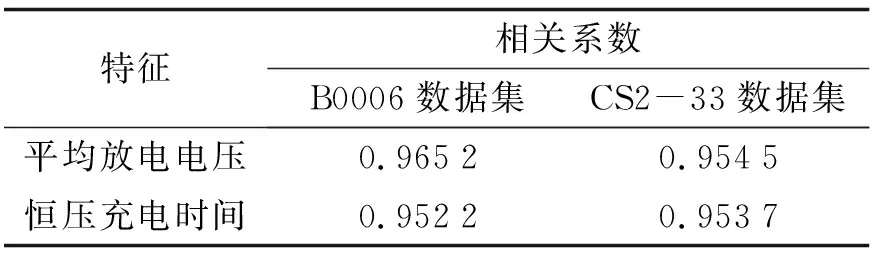
表1 數據特征相關性分析

從表1中可以看出，平均放電電壓、恒壓充電時間均與電池容量成正相關，而且相關系數接近1，說明相關性非常高. 這兩個特征包含充放電兩部分的電壓、充電時間等數據，并不包括單一的部分，具有代表性，因此選擇了這兩個特征. 此外，考慮到電池隨著充放電周期數的增加，整體容量呈現下降的趨勢，具有一定的時序性，可以看作時序序列數據. 因此在進行常規特征選擇的同時還考慮了之前電池容量值的影響因素，通過選擇之前5個電池容量值(即時序長度為5)和上述兩個特征構成了輸入特征矩陣，并選擇不同的預測起點來進行訓練預測. 根據EOL的定義，本研究選擇電池健康狀態(SOH)下降到70%時作為預測EOL點，對應兩個數據集的EOL周期點分別為110和530.

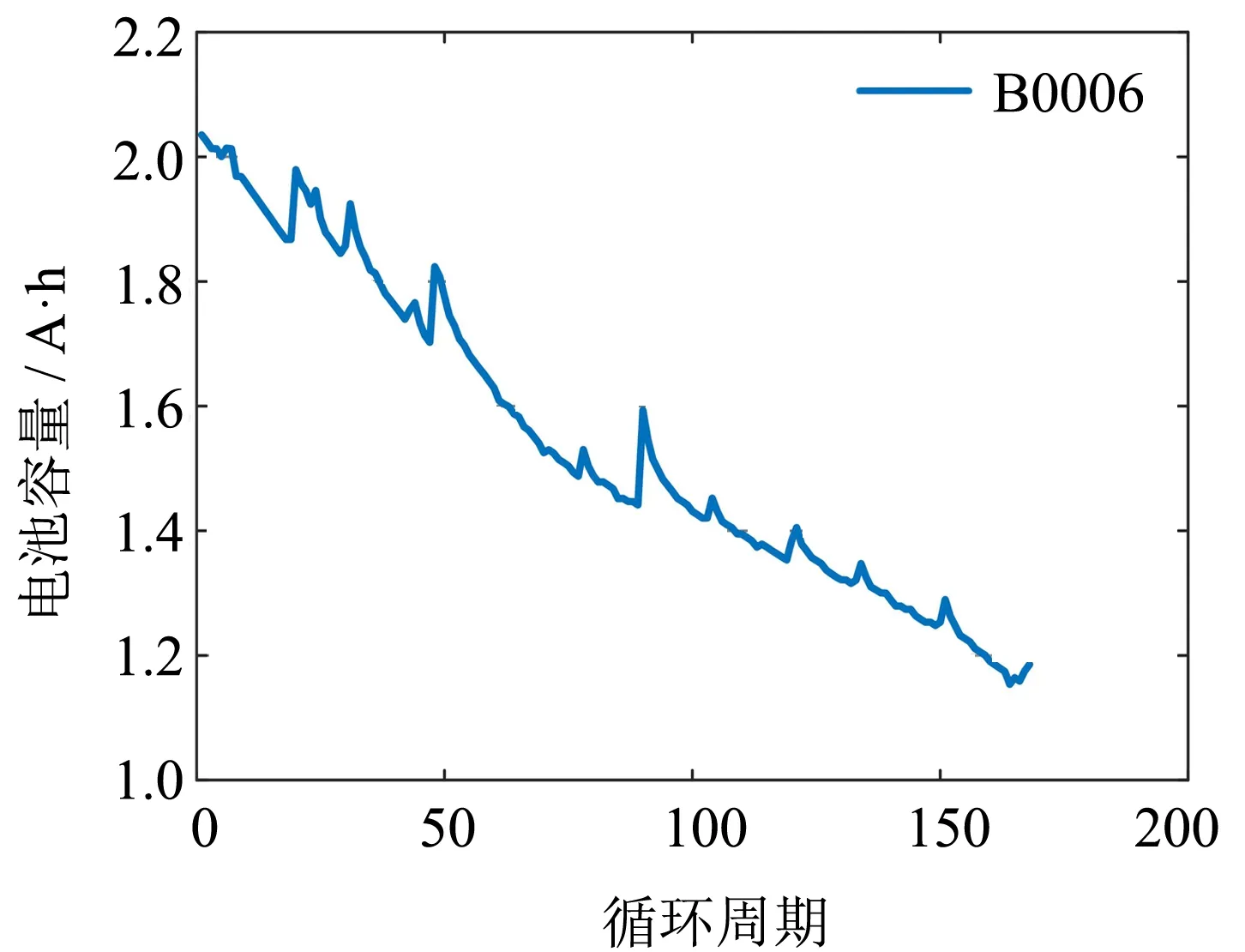
圖3 B0006數據集的電池容量變化曲線Fig.3 Battery capacity change curve of B0006 data set

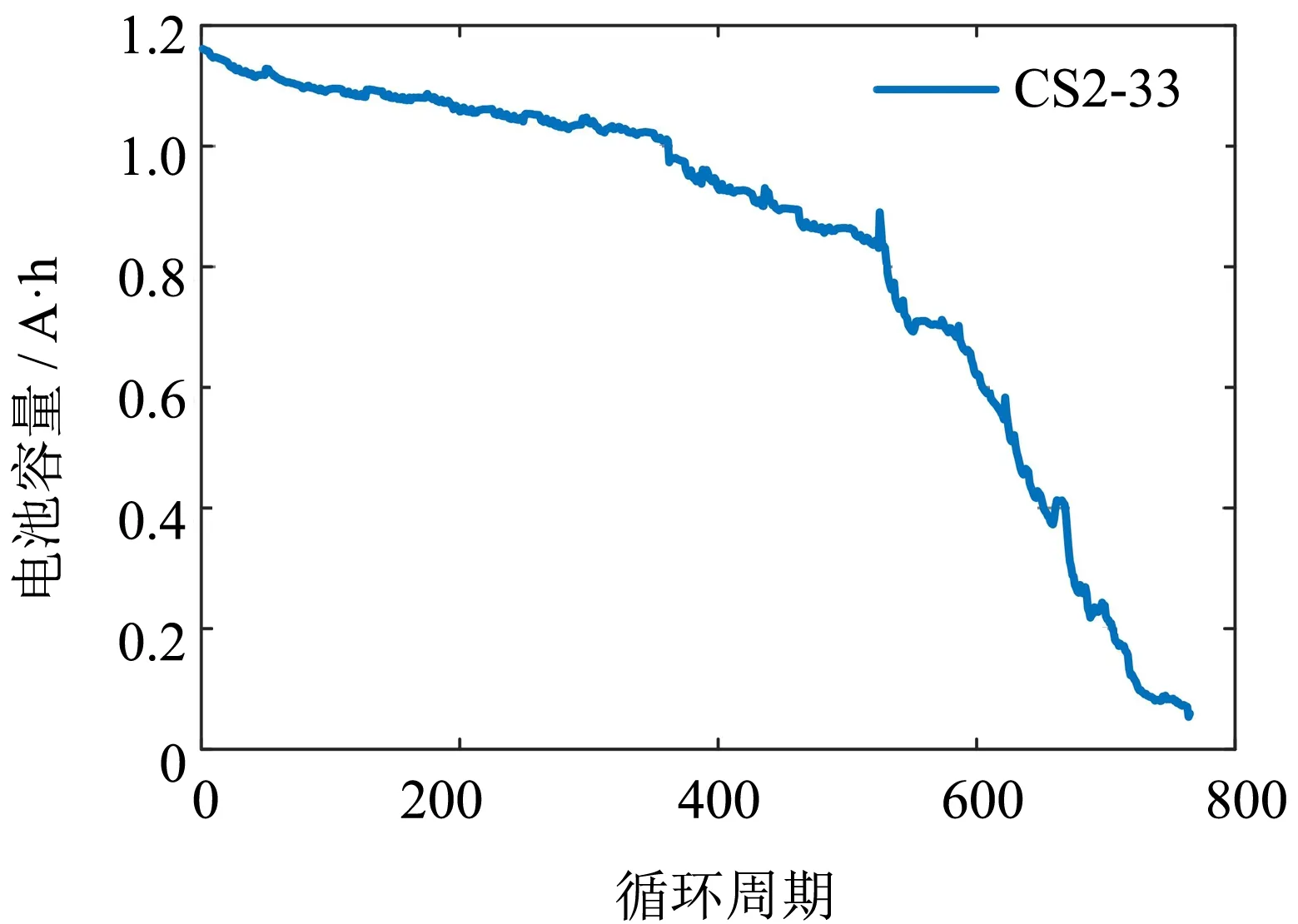
圖4 CS2-33數據集的電池容量變化曲線Fig.4 Battery capacity change curve of CS2-33 data set

2.2 評價指標

選擇均方根誤差(RMSE)、平均絕對誤差(MAE)、預測誤差周期RULe作為模型評價指標. 其中，RMSE一般是用來衡量預測值和真實值的偏差； MAE可以更真實地反映預測值和真實值的誤差情況； RULe是用來衡量達到EOL時預測值和真實值的誤差周期. 評價指標的計算如下所示：

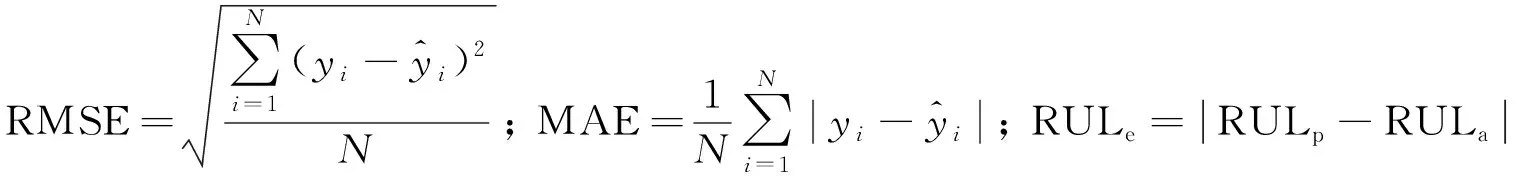
(5)

2.3 實驗結果

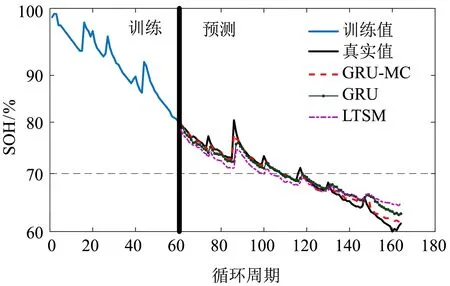
圖5 B0006電池預測起點60的結果對比Fig.5 Comparison of results of B0006 battery prediction starting point 60

以B0006電池為例，設置預測起點為60，GRU預測模型的參數設置為： 序列長度為5，隱藏層層數為1，隱藏層節點數為24，學習率為0.01，訓練次數為100，預測結果如圖5中曲線“GRU”所示. 對預測結果采用MC方法進行誤差修正，根據相對誤差劃分的三個狀態區間為{E1[-1.500，-0.010]；E2[-0.009，0.010]；E3[0.011，0.040]}，根據劃分的狀態區間統計預測結果的狀態轉移情況，得到了狀態轉移矩陣P如下：

根據步驟3計算得到修正后的預測值，最終的預測曲線如圖5中“GRU-MC”曲線所示.

從圖5可以看出，GRU預測模型能夠預測到電池容量的變化趨勢，達到EOL狀態時的預測周期與實際周期幾乎一致. 雖然LSTM也能擬合容量變化曲線，但是與GRU相比，預測誤差明顯較大. 在80～100周期異常值和120周期之后單純GRU算法的預測精度明顯下降，與實際值偏差較大. 而經過MC修正誤差之后，預測曲線明顯能夠更好地擬合實際曲線，預測精度明顯提高. 其他之前預測較準確部分也沒有發生經過誤差修正出現矯枉過正的現象. 這是由于MC算法對相對誤差進行狀態區間劃分導致后面進行誤差修正時，起初誤差較大的值能得到較大的誤差修正，而起初誤差較小的，得到的修正變化較小，對預測結果的影響較小. 從圖中可以看出還有一部分值的誤差較大，即使經過誤差修正，誤差沒有減小很多，這是因為異常值對于之前狀態的依賴性較小，導致了GRU預測結果不準確，MC對于這些個別異常值不夠敏感，只是按照所在的狀態區間進行誤差修正，如果狀態區間較小，就會導致修正較小. 綜上所述，經過誤差修正之后整體曲線的預測精度有所提升. 此外，將模型應用于B0006數據集的預測起點80和100進行預測，實驗結果如圖6～7所示. 從圖中可以看出，隨著預測起點越接近EOL點，訓練數據越多，所有算法的預測精度均有所提升，預測周期誤差不斷減小，而GRU-MC混合算法始終取得較小的RMSE和MAE. 實驗結果說明在B0006數據集上，GRU能夠較為準確地預測RUL的變化，MC能夠有效地對初步的預測結果進行誤差修正，使得預測結果更加準確.

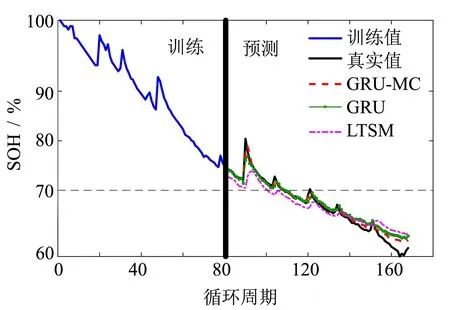
圖6 預測起點80的結果對比Fig.6 Comparison of results of prediction starting point 80

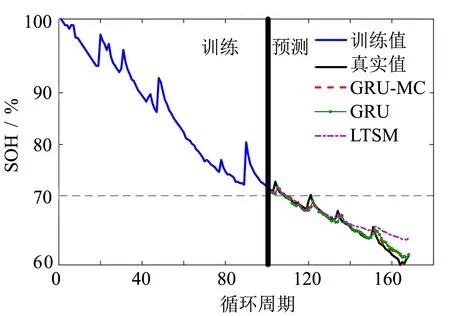
圖7 預測起點100的結果對比Fig.7 Comparison of results of prediction starting point 100

為了驗證模型的泛化性，在CS2-33數據集上進行電池RUL預測. 設置預測起點為300、350和400，實驗結果如圖8～10所示. 從圖中可以看出，GRU算法能夠較為準確地預測電池容量的變化趨勢. 在550周期之前，算法的預測誤差較小，在后面周期部分預測誤差變大. 這是由于CS2-33數據集是對電池完全充放電，最后的容量下降接近0，超過了電池的失效閾值. 而經過MC的誤差修正，最后部分的誤差明顯有所減小. 可以看出與GRU、卷積神經網絡(CNN)、LSTM相比，隨著預測起點越來越靠近失效點，GRU-MC的誤差周期幾乎沒變化. 這是由于GRU-MC在預測起點300時的誤差周期已經很小，約為1個周期，無論訓練數據的增加或者誤差修正，對誤差周期的影響已經不大. 但是RMSE和MAE均有所減小，預測曲線更接近真實曲線，證明了混合算法的魯棒性. 綜上所述，實驗結果證明了本研究所提出方法的準確性和泛化性.

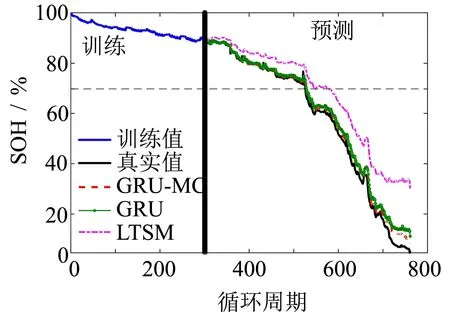
圖8 預測起點300的結果對比Fig.8 Comparison of results of prediction starting point 300

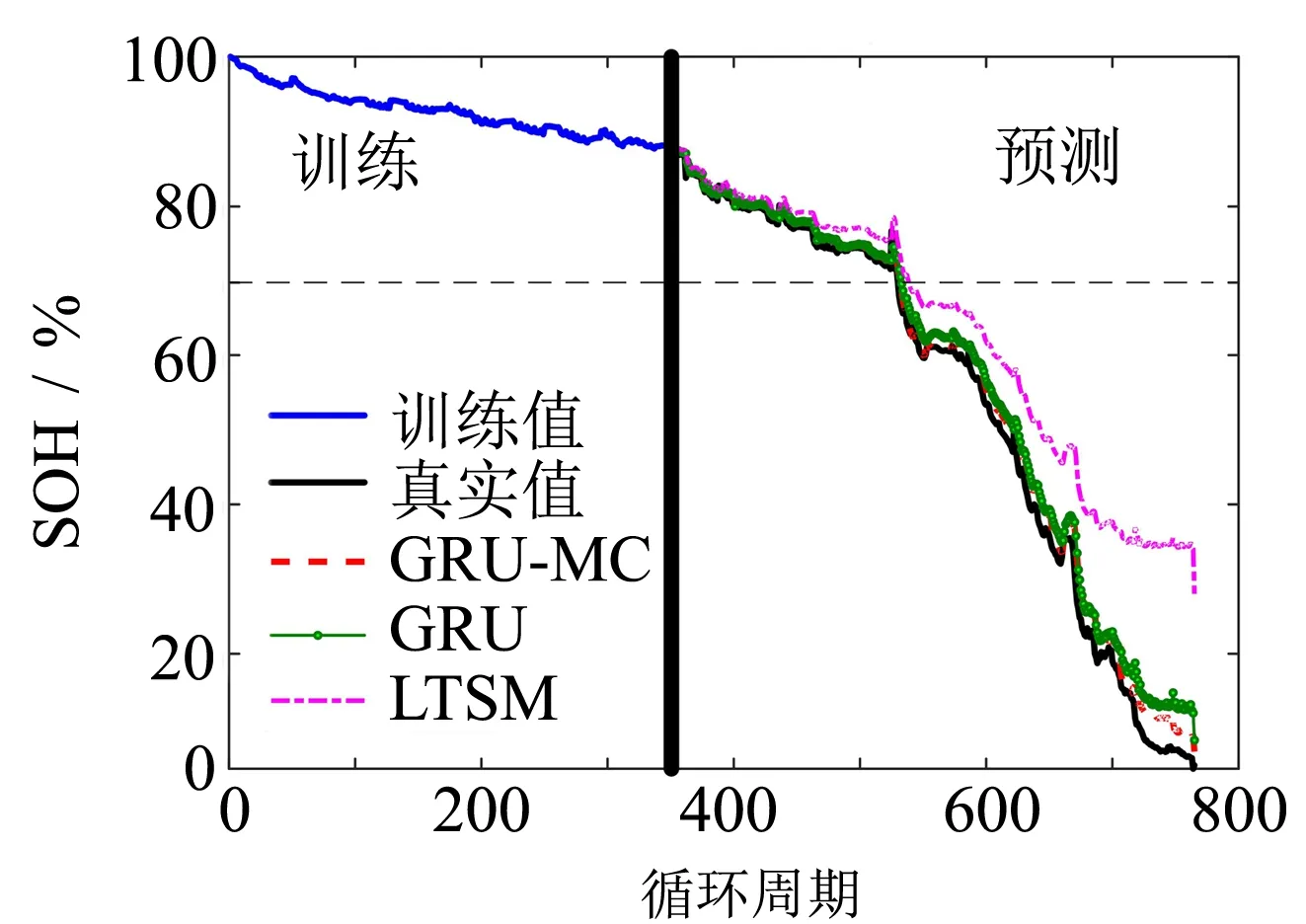
圖9 預測起點350的結果對比Fig.9 Comparison of results of prediction starting point 350

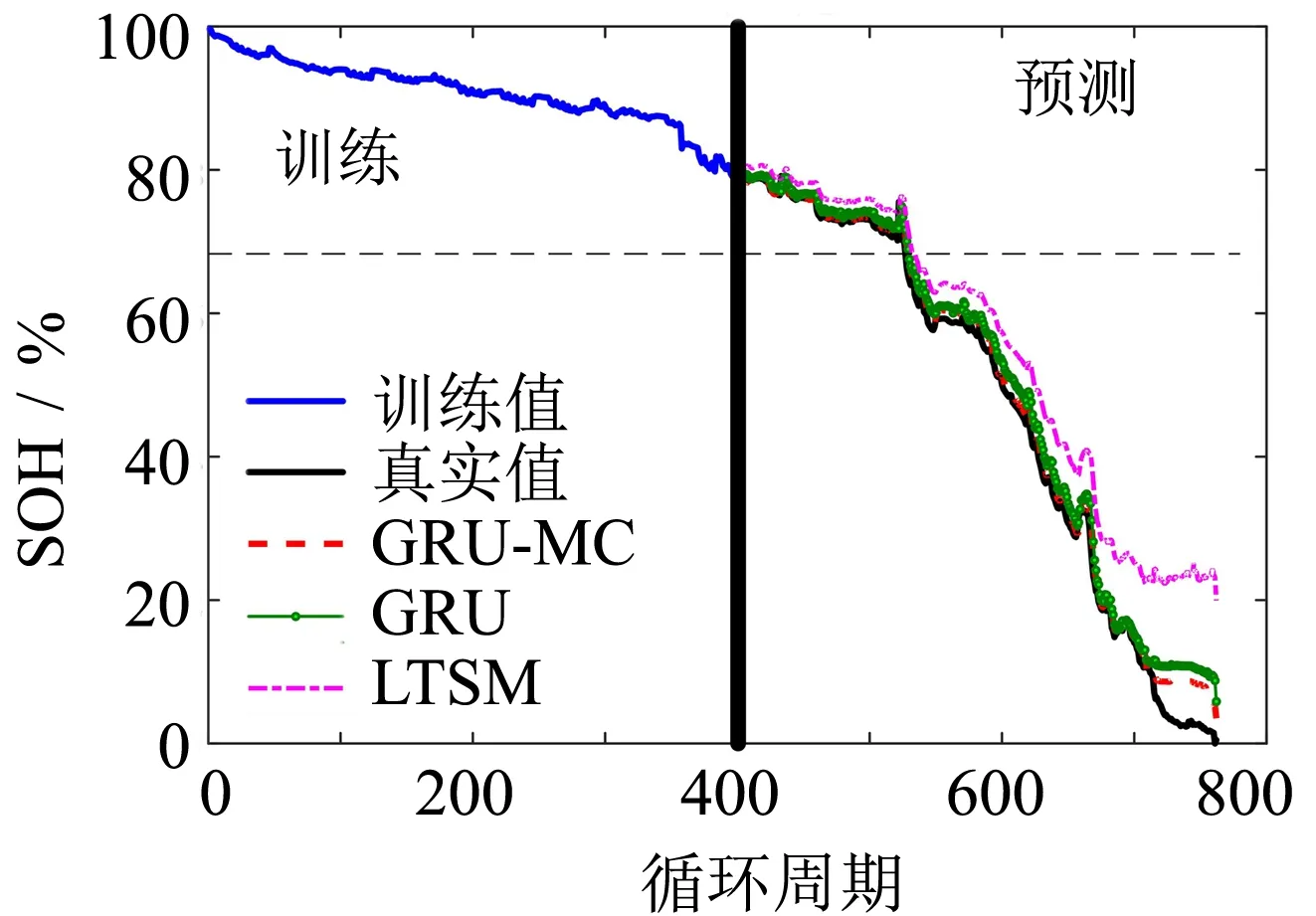
圖10 預測起點400的結果對比Fig.10 Comparison of results of prediction starting point 400

3 結語

本研究提出一種基于GRU-MC混合算法的鋰離子電池剩余使用壽命預測方法. 首先，對數據進行預處理和特征提取，根據GRU模型的特型選擇構建合適的輸入特征矩陣，然后搭建基于GRU的預測模型，并使用MC方法對預測結果進行誤差修正，使RUL的預測更加準確和穩定. 在B0006和CS2-33公共數據集上驗證了GRU-MC混合算法的預測性能，實驗結果表明，所提出方法RUL總的預測誤差約為1個周期，RMSE約為1.2%～2.2%. 與未經過MC方法誤差修正的結果相比，預測結果有了較明顯的提升，RMSE減少了約0.9%～1.4%； 與其他RUL預測方法相比，所提出方法的預測結果較為準確. 綜上所述，本研究提出的GRU-MC混合算法能夠較為準確地預測鋰離子電池RUL，能夠確保電動汽車中電池管理系統的安全可靠運行.