改進貝葉斯判別法的礦井水源識別模型

秋興國，劉 杰，李 娜，黃潤青

(西安科技大學 計算機科學與技術學院，陜西 西安 710054)

0 引 言

中國是世界主要產煤國之一，也是受煤礦水害最嚴重的國家之一[1]，在煤礦井下發生的水害水災是礦井安全工作中的關注重點[2]，礦井水害一旦發生將會造成極為嚴重的人員傷亡及財產損失，所以只要及時準確地識別礦井水源就可以采取有效的防治措施。因此，在水害防治工作中，對于礦井水源識別工作是重中之重。目前，水源識別方法包括地下水化學特征分析法、多元統計方法(判別分析法和聚類分析方法)和非線性分析方法(模糊數學法、神經網絡法和可拓識別法等)[3-4]。陳俊環等利用水質類型的差異，對礦井水源進行判別，并說明水化學分析法存在一定的局限性[5]；袁文華等將水溫水位判別法應用于煤礦水源的判別，建立地溫方程計算含水層水溫，與實際監測點水溫進行比較來判別礦井水源[6]；孫福勛等利用Fisher判別理論，結合質心距評判法對礦區水樣進行了分析判斷[7]；代革聯等在煤礦中引用模糊聚類判別法，分析了水質類型相似時水源判別不準確的問題[8]；徐星等利用神經網絡仿真結果誤差小的特點將其應用于礦井突水水源判別領域[9]；張瑞鋼等利用可拓識別方法判別礦井突水水源，還有一些未確知數學方法等[10]。而上述方法各有適用性，如有的模型復雜、判別過程繁瑣、確定離子權重時主觀性較強、對誤判損失有失考量[11]，在準確率方面也需要提高等，因此礦井水源識別的算法研究還需進一步深入。

貝葉斯判別法具有判別模型簡單、求解速度較快和判別質量高的特點[12]，在貝葉斯判別法的基礎上，結合主成分分析方法，并引入變異系數來進行評估計算過程中水質離子的權重，以消除水源判別過程中離子指標間存在信息疊加以及評價過程中主觀因素過重帶來的影響[13]，提高水源判別的準確率，從而減少實際應用中礦井水源類別的誤判。

1 理論與算法

1.1 主成分分析法

主成分分析法(principal component analysis，PCA)是一種降維的統計方法，將可能互相關聯的多個元素進行數據壓縮，重新組合成一組新的相互無關的元素，達到以盡可能少的數據來表示大部分信息的目的[14]。

由于在數據處理過程中難免會遇到高維數據組，由于數據維數較高變量較大，這些變量之間往往會存在一些相關性，因此這些數據樣本很難反映總體的主要特征[15]。主成分分析將可能具有相關性的高維變量經過線性變換合成線性無關的低維向量，用來提取較少個數的重要變量。在礦井水源識別工作中，經過主成分分析可以在保留主要信息的基礎上降低向判別模型輸入的維數，減小輸入信息量，達到以少量的水質離子就可以代表某類水源的目的，若主成分選取有誤差，在實際的水源識別工作中則會類別模糊不清或對最終的判別結果產生影響。利用Statistical Product and Service Solution(SPSS 24)對原始數據進行主成分分析處理。

假設對某一事物的研究涉及N個樣本，每個樣本有n個變量，分別用X1,X2,…,Xp表示，對隨機變量進行線性變換形成新的綜合變量Y[16]，即

(1)

式中ci1+ci2+…+cin=1；Yi與Yj(i≠j;i,j=1,2,…,n)互相無關；Yi為(Y1，Y2，…，Yn)的線性組合中方差最大者；Y2為與Y1不相關的(X1，X2，…，Xn)所有線性組合中方差最大者；Yn為與(Y1，Y2，…，Yn-1)都不相關的(X1，X2，…，Xn)的所有線性組合中的方差最大者[17]。基于以上原則確定的綜合變量(Y1，Y2，…，Yn)分別稱為樣本的第1，第2，…、第n個主成分[18]。主成分分析法的主要過程如下。

1)對原始數據進行標準化處理，排除數量級和量綱對結果造成的影響。

2)計算各標量之間的協方差矩陣及相應特征向量與特征值。

3)計算第k個主成分的方差貢獻率(k=1,2,…,n)。

4)按照累積方差貢獻率>80%或特征值大于1的原則選取主成分[19]。

1.2 貝葉斯判別法

貝葉斯(Bayes)是先通過已給定的訓練集，以特征詞之間的獨立作為前提假設，學習從輸入到輸出的聯合概率分布，再基于已學習的模型，輸入X輸出擁有最大后驗概率的Y，其中X=(x1,x2,…,xn)為判別指標；n為判別指標的維數；Y為類別[20]。

1.2.1 貝葉斯模型

貝葉斯計算公式為

(2)

式中Bi為水源類別；A為水樣；P(Bi)為先驗概率，即未經計算僅通過經驗和直覺來判斷該水樣屬于某種水源的概率；P(A|Bi)為條件概率，即當水樣屬于不同水源時出現某種水質離子的概率；P(Bi|A)為后驗概率，即當獲得水質離子測量值的條件下該水樣屬于某種水源的概率。

針對礦井水源水質離子的特點，將貝葉斯模型細化，并對貝葉斯模型中的參數做進一步調整：i為水樣中的水質離子指標；j為某種水源；(i=1,2,3,…,n)(j=1,2,3,…,m)。因此，原貝葉斯公式修改為

(3)

式中xi為水樣中第i個水質離子的監測值；yij為當水源種類為j時水質離子i的標準值。

1.2.2 貝葉斯模型計算步驟

1)計算P(yij)，即未經計算水質離子就判斷該水樣屬于哪種水源，此時水樣屬于每種水源的概率值相同。

(4)

2)計算P(xi|yij)，此處采用距離方法[21]，即取水質離子的監測值與標準值間距離絕對值的倒數進行計算[22]，即

(5)

式中Lij=|xi-yij|，(i=1,2,3,…,n)。

3)計算，P(yij|xi)按照式(3)計算。

4)求多種水質離子綜合時水樣屬于水源的概率，其中ωi為水質離子i的權重。

(6)

5)以最大概率確定水樣歸屬

(7)

1.3 變異系數法

變異系數法(coefficient of variation method)是利用各項指標所含信息來計算指標的權重，是一種客觀賦權方法。這種方法的基本做法是：在評價體系中取值越大的指標，越能反映該項指標的重要程度。變異系數越大說明該離子的重要程度越大，該水質離子在水樣中起的作用就越大，越能代表該水樣，故可用變異系數確定的變異性權重來確定水質離子的重要程度。通過變異系數法來計算權重，避免了主觀賦權方法中專家的偏好對結果的影響[23-24]。數據處理步驟如下。

1)數據標準化

將第i個指標的實際數值記為Xi，該組數據的最大值記為Xmax，最小值記為Xmin，數據標準化之后的值記為Zi，通過公式計算[25]。

(8)

(9)

3)計算各指標賦權重

(10)

1.4 改進貝葉斯判別的礦井水源判別模型

在對主成分分析、變異性權重和貝葉斯判別模型相結合后，構成了改進貝葉斯判別模型。并在此基礎上建立起改進貝葉斯礦井水源識別模型(圖1)。

圖1 改進貝葉斯判別的礦井水源識別模型Fig.1 Mine water source identification model of improved Bayesian discrimination

礦井水源識別模型的實驗步驟(圖2)為：①整理水源數據，進行數據標準化，計算協方差矩陣、特征向量、特征值，寫出主成分并根據主成分貢獻率來選取在水源中起主要作用的水質離子；②根據總水源種類計算水樣的先驗概率；③計算變異系數，在多指標綜合計算概率時代替原公式中的權重w(數據標準化、計算標準差和變異系數)；④推求多指標綜合下的后驗概率；⑤以最大概率歸屬原則確定該水樣歸屬。

圖2 改進貝葉斯判別模型結構Fig.2 Model structure of improved Bayesian discrimination

2 礦井水源判別模型建立

2.1 數據準備

2.2 主成分分析法

在相關系數矩陣中，若相關性小于0.3，說明離子間存在弱相關；若相關性在0.3與0.6間，說明離子直接存在中等強度關系；若相關性大于0.6，則離子間存在強相關關系(表2)。說明各水質離子間存在相關關系和重疊信息，例如Ca2+和Mg2+關聯度達到了92.9%。若直接使用冗余重疊信息進行判斷，有可能會對判別結果產生影響，所以要進行降維來減少參與判別模型的水質離子數量。

表2 水化學指標相關系數Table 2 Correlation coefficients of hydrochemical index

通過對各主成分進行方差貢獻率(表3)分析，可以根據需要來選取需要的主成分。前5個水質離子的累積方差貢獻率達到了99.55%，說明這5個水質離子幾乎完全可以代表水樣中所有離子的特征。

表3 成分方差貢獻率Table 3 Contribution rate of component variance

2.3 權重確立

根據2.2確定的2.1表1中(1-26號)主要水質離子，以及1.3對于變異系數法的論述，通過MATLAB軟件實現各主要水質離子的權重的計算(表4)。

表4 變異性權重

2.4 貝葉斯模型及判別結果

根據1.2中貝葉斯方法的原理及步驟，對表1中作為數據標準的數據(1～26號)進行回代檢驗以及對表1中待檢測樣本數據(27～40號)進行判別并與直接貝葉斯判別進行對比。

表1 屯蘭礦水化學特征Table 1 Hydrochemical characteristics of Tunlan mine

在14個礦井水源數據待判樣本中，改進的貝葉斯模型判別正確個數為 11個，原始貝葉斯模型判別正確10個。基礎貝葉斯判別誤判個數為5個，總體正確率為64.29%，而改進的判別模型誤判個數為2個，總體正確率為85.71%(表5)。

表5 預測結果對比Table 5 Comparison of prediction results

從表6可以看出，在26個回代數據中，改進的貝葉斯模型判別正確個數為25個，原始貝葉斯模型判別正確 24個；貝葉斯判別正確率為92.31%，改進的貝葉斯方法正確率為96.15%。結果表明，改進后的方法更加準確，判別準確率更高。

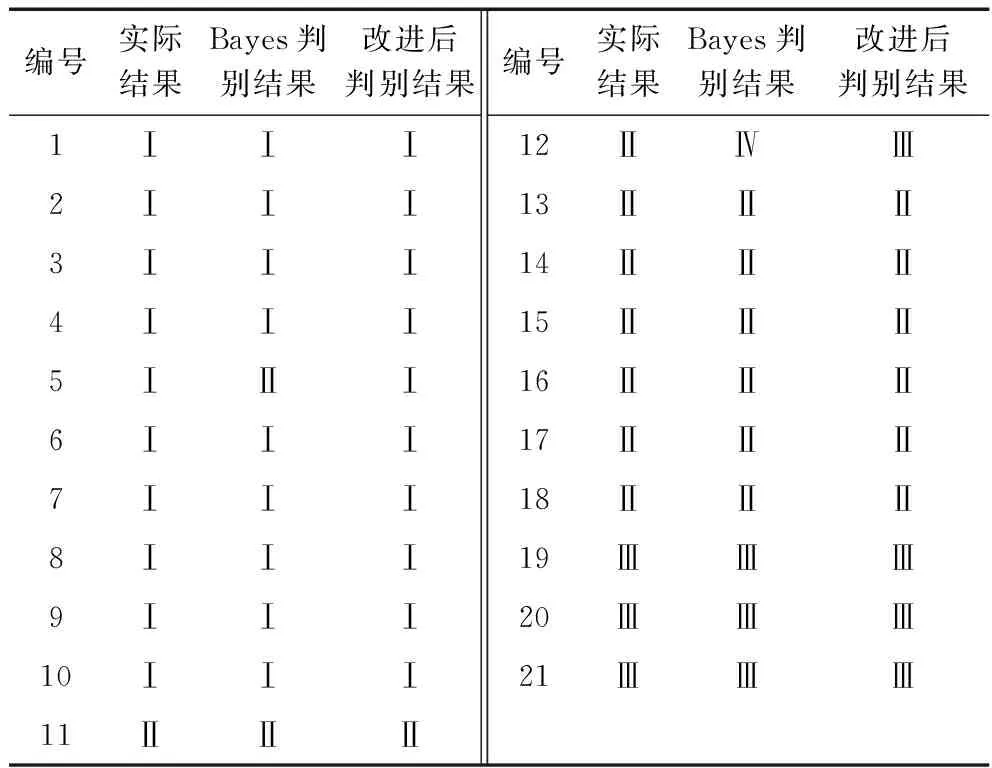
表6 樣本回代結果Table 6 Sample back-substitution results

根據基礎貝葉斯判別模型和改進貝葉斯判別模型，對待測樣本進行水源類型的歸屬判別。從結果(圖3)中可以看出第5，第6，第9，第11，第13個水源數據類別判別有誤，而改進后的貝葉斯判別法后只在第6，第9個水源類型判別有誤。

圖3 預測結果對比Fig.3 Comparison of prediction results

圖4表示對樣本數據回代進行水源類別的歸屬判別，在實驗中基礎貝葉斯判別在第5，第12個水源數據類別判別有誤，而改進后的貝葉斯判別法僅在第12個水源數據判誤。

圖4 樣本回代結果Fig.4 Sample back-substitution results

在待測樣本數據類型判別中改進的貝葉斯模型較基礎貝葉斯模型的準確率從64.29%提升到85.71%，提升了21.42%，而回代樣本從92.3%提升到96.15%，提升了3.85%，說明改進后的算法準確率有顯著的提升(表7)。

表7 模型預測結果比較Table 7 Comparison of model prediction results

3 結 論

1)經主成分分析后的水質離子維數降低，降維后的數據能夠很好地保留原數據的基本信息，提取出起主要作用的水質離子，避免因信息疊加和人為選取水質主成分的主觀性；通過變異系數來客觀賦予權值可去量綱化及消除人為賦予權值的影響，并且較為客觀地反映水質離子在樣本中的重要程度，能夠識別指標數據的變化信息。

2)樣本回代組和樣本測試組的判別準確率較傳統貝葉斯模型有明顯提高，判別結果可信度高，為水源判別提供了一種新的識別思路，可為礦山防治水提供依據。