基于穩健估計局部多項式插值定權模型分析

2022-04-28 04:06:56劉亞靜李勝男王誠聰

西安科技大學學報 2022年2期

劉亞靜，李勝男，王誠聰

(1.華北理工大學礦業工程學院，河北唐山 063210;2.中國科學院東北地理與農業生態研究所，吉林長春 130000)

0 引言

局部多項式插值法是一種局部加權最小二乘擬合，根據有限個已知采樣點數據，采用多個多項式來進行曲面的擬合[1]，每一個插值點的預測值都對應一個多項式，利用局部多項式插值法得到的曲面，能夠較好地描述短程變異[2]。在測量過程中，由于受到諸多因素的影響，會使測量數據中含有粗差，使得觀測值將不服從正態分布，若直接使用這些數據進行曲面插值，其結果很難與真實情況相吻合[3]。抗差估計解決了這一問題，即使用等價權函數來代替一般權函數，對含粗差的數據進行降權處理，則可以有效提高模型的抗差能力。

在現有研究中，吳富梅等利用水準網數據，對選權迭代法的幾種權函數在不同顯著性水平下的抗差性進行了比較，認為當數據不穩定時，IGGⅢ和丹麥法的抗差效果略優于其他權函數[4]。徐波、楊勇喜等通過坐標參數轉換實例對選權迭代法進行分析，發現通過IGG函數進行定權可有效降低含粗差觀測值的權值，在進行三維坐標轉換時能獲取更高精度的轉換參數[5-6]。孫同賀等將具有穩健初值的選權迭代法融入到DEM粗差探測中，證實穩健初值的選權迭代法具有很強的穩健性和粗差探測能力，可以實現對粗差的探測和剔除[7]。HOLLAND等提出選權迭代法，可通過反復迭代，逐步減小粗差觀測值的權重，從而進行粗差定位和剔除[8]。穩健估計選權迭代法具有很好的抗差能力[9]，但其相關研究大多是針對水準網測量和坐標轉換方面的研究，對于多項式插值采樣點的定權鮮有闡述。

一般認為DEM誤差來源于源數據的采樣誤差和DEM插值過程中的插值誤差[10]。在進行多項式插值時，常用的采樣點定權函數包括反距離加權法和局部距離比法，但對于含粗差的觀測數據，這2種傳統的方法會將粗差當作一般數據處理，導致在構建曲面模型時粗差引入，使得曲面發生歪曲[11-14]。因此文中將穩健估計選權迭代法與局部多項式插值進行結合，分別采用傳統的反距離加權法和穩健估計選權迭代法中的Huber權函數法、Andrews權函數法、IGG方案對局部多項式插值的采樣點進行定權，通過均方根誤差(root mean squared error，RMSE)對各方法的擬合精度進行比較分析，并且對比分析采用不同定權方法得到的插值曲面和預測高程相似度，探討所引進的3種定權方法中，在數據含有粗差時采用不同定權方法降低含粗差觀測值的權[15-17]，對于含粗差數據插值擬合效果最優的方法，以提高其插值精度，對局部多項式插值的定權模型改進，為局部多項式插值曲面的建立提供保證。

1 局部插值理論模型與精度評定

1.1 動態球半徑選點法

動態球半徑選點法是以內插點為球心，R為半徑，選取各內插點周圍可用來計算的采樣點[18-19](圖1)。半徑R可通過構造函數來確定

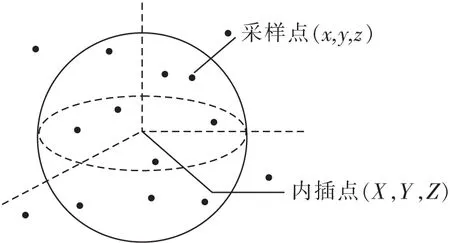
圖1 動態球半徑選點法原理示意Fig.1 Schematic diagram of dynamic sphere radius point selection method

(1)

式中N為采樣點總數，個；A為研究區域面積，m2；n為規定界限球內的采樣點數,個。

1.2 二次曲面模型

高精度曲面的繪制必須保證每一個數據點在權值其有效范圍內平滑過渡[11]，采用二階可導的二次曲面來建立局部曲面模型，其二次曲面模型表達式如下

z=f(x,y)+ε

(2)

f(x,y)=a0+a1x+a2y+a3xy+a4x2+a5y2

(3)

式中z為插值點高程值，m;ε為擬合殘差;f(x,y)為二次曲面點的內插值,m，ai(i=0,1,2,…,5)為多項式系數；x和y分別為平面采樣點的橫縱坐標。

通過最小二乘原理，求解多項式系數，矩陣表達形式如下

Z=B×A+ε

(4)

A=(BTPB)-1(BTPε)

(5)

矩陣表示為

1.3 精度評定

選用均方根誤差(RMSE)進行擬合優度的評價，當預測值與真實值相同RMSE=0，誤差越大，該值越大。均方根誤差計算公式為

(6)

2 采樣點權函數

采樣點權函數可以用來反映采樣點與內插點的相關程度。對區域內的采樣點賦權，權重(Pi)的確定與該點到內插點的距離(di)有關，距離越小，該點對內插點的影響就越大，權重也越大。可采用反距離加權法、Huber權函數、Andrews權函數和IGG方案4種方法確定采樣點的權重。

多具有不規則狀晶形，與石英、云母等脈石礦物關系密切，少部分與黃鐵礦連體，白鎢礦中含鎢約為60.81%，粒度主要為中細粒，占75.14%，部分為微細粒，占12.02%，少量為粗粒，約占12.82%。礦石中的白鎢礦解離度較好，-0.074 mm含量占65%的磨礦細度下，92.73%的白鎢礦已單體解離，6.49%的白鎢礦與脈石礦物共生。因此，白鎢礦主要分為兩類，一類多數為單體解離，但粒度大小差別較大。另一類粒度較細，與脈石礦物與石英、長石等脈石礦物共生或呈港灣狀接觸，或包裹于脈石礦物顆粒中。

2.1 反距離加權法

反距離加權法是常用的采樣點定權法。該方法依據相近相似的原理[20]，采樣點權重的大小會隨著其與插值點之間距離的增大而減小，距離插值點越近，采樣點的權重就越大[14]。

(7)

(8)

式中di為內插點到采樣點的距離，m；X，Y，Z分別為內插點的坐標；xi,yi,zi分別為采樣點的坐標。

2.2 穩健估計權函數

采用穩健估計權函數進行采樣點的定權，是以內插點與采樣點之間的距離為自變量，內插點的值為因變量[18]，通過采樣點權函數計算其權重。權函數分別選用Huber權函數、Andrews權函數和IGG方案，其中Huber函數包含正常域和可疑域，只對可疑域內的觀測值進行降權處理，不能將有害信息剔除掉；Andrews函數包含可疑域和淘汰域，將所有的觀測值都進行降權處理；而IGG方案同時擁有正常域、可疑域和淘汰域，充分利用所有觀測數據[4]。

2.2.1 Huber權函數

Huber權函數確定的權因子為

(9)

式中ω為采樣點權因子；u為采樣點殘差。

2.2.2 Andrews權函數

(10)

式中ω為采樣點權因子；u為采樣點殘差。

2.2.3 IGG方案

IGG方案是由周文江教授最初提出的[21]，該方案將數據劃分為正常、可用和有害數據，同時，將權分區為保權區、降權區及淘汰區，充分考慮測量數據的實際情況，很好地將不同權重函數和容差標準用于不同的測量數據。由IGG方案確定的權因子[16]為

(11)

式中vi為第i個測量的殘差；σ0為標準偏差；k，r為閾值的調制因子，其中k=1.0～1.5，r=2.5～3.0，該方案k=1.5，r=3.0。

由式(11)可知，IGG方案將權重確定分為3部分，采用不間斷抗差標準[22]：當殘差不大于kσ0時，采用最小二乘法，其權重仍為1；當殘差介于kσ0與rσ0時，則采用殘差反比例減少法，降低對其權重，以減弱對參數識別的影響；當殘差大于rσ0時，其權重為0，即淘汰此測量數據，充分體現IGG方案的抗差能力。

3 案例分析

3.1 數據來源

實驗采用《ArcGIS地理信息系統空間分析實驗教程》中的實驗數據。該組數據共有170個采樣點，分布均勻，屬性字段分別是橫坐標x，縱坐標y，以及高程z。部分采樣點數據見表1。

表1 部分采樣點數據Table 1 Partial sampling points data

為驗證Huber函數法、Andrews函數法及IGG方案對含有粗差數據的抗差性強度區別，在實驗數據中隨機加入3組粗差。運用MATLAB軟件進行曲面插值和擬合，并在三維空間中顯示出來(圖2)，同時將穩健估計采樣點定權3種方法預測得到的高程數據進行對比分析，通過散點圖表示(圖3)。

圖2 曲面擬合結果對比Fig.2 Comparison of curved surface fitting results

圖3 插值結果相似度對比Fig.3 Similarity comparison of interpolation results

3.2 插值曲面對比分析

對比分析圖2中的擬合曲面效果，可以看出選權迭代法對含有粗差的數據進行定權的插值結果與無粗差數據時結果很接近，效果較好，圖中標注的部分為插值曲面中差異較明顯的區域。

3.3 預測高程相似度對比分析

將采用反距離加權法對無粗差數據計算出的高程，與采用穩健估計權函數對于含粗差數據計算出的高程，通過散點圖(圖3)來反應其結果的相似程度。縱軸代表數據無粗差時采用反距離權重法定權得到的高程值，橫軸表示采用選權迭代法計算出的高程值。

圖3中3幅圖像數據點的分布均呈現出y=x的趨勢，但由IGG方案定權后進行插值擬合的效果更好，說明當數據存在粗差時，3種選權迭代法中，采用IGG方案對采樣點進行定權預測的內插點高程值，與數據無粗差時常用的反距離權重法進行定權計算得到的高程結果最為接近。

3.4 擬合優度對比

當測量數據含有粗差時，通過對比4種采樣點定權方法得到的均方根誤差(RMSE)評價其曲面擬合優度(見表2)，RMSE越大，則說明預測值與真實值的誤差越大[23-26]，即抗差性越弱。由表2可知，當高程數據含有粗差，采用傳統的反距離加權法進行插值時，RMSE值為1.433 3，相比之下，Huber函數法和Andrews函數法插值得到的擬合優度更高，分別是0.742 8和0.683 2，表明穩健估計選權迭代法具有一定的抗差能力。當采用IGG方案對采樣點進行定權時，RMSE最小為0.531 8，可以看出該方法的抗差能力最強，因此可以推斷當觀測數據存在誤差時，所用的3種方法中，IGG方案對采樣點定權所得到的高程值與真實值最為接近，擬合度最高，插值效果最好。