一種融合區域生長和RANSAC的稠密點云平面分割方法

張建偉，權慶樂

(河南牧業經濟學院 信息工程學院，河南 鄭州 450004)

0 引 言

近年來，隨著三維激光掃描技術的快速發展，高精度、數據海量的稠密點云已廣泛應用于逆向工程[1]、文物修復[2]、3D打印[3]、自動駕駛[4]等領域。如何從點云中快速、準確地提取出真實場景目標信息，已逐漸成為國內外眾多學者的研究熱點。平面結構由于具有良好的幾何特性，廣泛地存在于室內外各場景中。魯棒的平面結構可為場景結構建模[5]、機器人導航定位[6]等提供穩定的特征信息。稠密點云由于其數據細節豐富，可以較為魯棒地反映真實地物信息，但由于其數據海量，如何高效準確處理成為難題。因此稠密點云中快速準確地提取平面結構已成為計算機領域中重要的研究內容[7-8]。

國內外眾多學者針對平面提取已做了部分研究，而目前的平面分割方法可總體分為模型擬合類方法、深度學習類方法和區域生長類方法。

1)模型擬合類方法。主要包括隨機采樣一致性算法(RANSAC)[9-10]和霍夫變換算法(Hough transformation)[11]。RANSAC算法首先預先設定平面參數，依據點到平面的距離，在全局范圍內將三維點分為外點與內點，并將內點數最多的點集作為最終平面分割結果。部分學者對RANSAC方法進行改進，SCHNABEL等提出采用八叉樹優化RANSAC算法，以提高平面提取效率[12]。熊風光等提出將K均值聚類與RANSAC相結合，以提高算法中的粗差點剔除率，在一定程度上提高了RANSAC算法的準確度[13]。RAGURAM等采用附加法向矢量的方式提取數據中的三角面片。以上方法雖然有較好的抗噪性，但計算效率較低，同時未考慮空間連通性，易在稠密點云數據中產生偽平面[14]。

霍夫變換算法將原始空間中平面檢測問題轉化為尋找參數空間峰值問題。目前主要模型有球體、直線、柱體和平面等。田朋舉等提出一種基于2DHough變換和八叉樹相結合的方法，實現建筑平面的有效分割[15]。HULIK等采用矢量約束來提高Hough變換算法檢測平面的準確度。但該類方法存在一定的平面誤識別現象[16]。

2)深度學習類方法。通過構建卷積神經網絡，對點云數據進行語義信息分割。以PointNet[17]、PointNet++[18]、PointCNN[19]等深度神經網絡為代表，可有效實現在真實場景下，提取點云數據中平面結構。YU等針對稀疏點云特性，提出網絡模型，提高平面擬合精度，但在稠密點云數據中的計算效率仍有待提高[20]。該類方法需大量樣本清洗及模型訓練等工作，當處理大規模稠密點云時，與傳統方法相比并無顯著優勢。

3)區域生長類方法[21-22]。通常是利用法線、曲率等幾何屬性，分析點云局部空間的鄰接關系，進而實現平面點云的生長。薛婧雅等提出基于超體素與區域生長相結合的方式提高屋頂平面的分割精度[23]。王沖等采用動態分配權重的方法來提高法線解算精度，進一步提高區域生長算法的準確性[24]。FOTSING等采用ICP算法選取可靠的候選種子點，并在生長過程中采用體素表達點云，改善平面分割質量[25]。ZHANG等提出一種基于2D和3D相互投影的區域生長方法，通過點云以及投影平面的幾何信息選取初始種子點，并通過區域生長條件判斷每個點的通視性，改善分割效果[26]。該類方法提取平面精度較高，但受到區域生長條件限制，平面結構的完整度有待提高。同時該方法更關注于點云局部空間變化，對于平面結構的整體考慮不足。

近年來一些學者也提出一些新方法，ZHU等將平面分解為多個平面段合并的結果，采用準逆理論(quasi-a-contrario theory)利用誤警值(false alarms)評估每個平面段的分割效果[27]。WANG等用L0梯度最小化算法的區域生長以及圖分割(graph cut)提取物體表面[28]。FATEMEH等提出多平面算法用于區分多平面立面的結構和非結構元素，從統計上考慮點組相對于其鄰居的位置，以進行識別的隔離多平面建筑的主立面[29]。

目前眾多研究方法多集中于某一類平面分割方法，并在此基礎上進行優化，而忽略各類方法之間的關聯性。模型擬合類方法具有嚴格的數學模型，但是忽略了局部空間結構的連續性。區域生長類方法強調局部空間中連續，而未對數據進行整體限制考慮，而過于嚴格的曲率閾值則會導致平面結構的不完整。因此，綜合以上各類平面分割方法的特點，提出一種區域生長和RANSAC相結合的稠密點云平面分割方法。融合2類平面分割方法中數學模型以及局部空間約束的優點，克服空間不連續及平面完整度不高的缺點。首先采用3種濾波方法實現點云初步的預處理，然后采用混合區域生長算法實現平面結構的初分割，其次利用平面彎曲度約束對平面結構的幾何狀態進行判斷，最后采用RANSAC算法剔除異常平面的粗差點，從整體提高平面分割的準確度。該方法綜合RANSAC和區域生長平面分割方法的優點，在一定程度上提高平面分割的準確度與完整度。

1 平面分割方法

1.1 技術路線

平面分割技術路線如圖1所示。首先對原始稠密點云進行預處理，利用無效點剔除、統計濾波、體素濾波，顯著降低點云數據量，濾除大量離群噪聲點。然后提出一種混合區域生長分割方法實現場景中平面點云的初分割。其次以整個平面為基礎對平面進行彎曲度約束分析，檢測出彎曲度異常平面。最后采用RANSAC算法剔除平面粗差點，提高平面分割準確度和完整度。

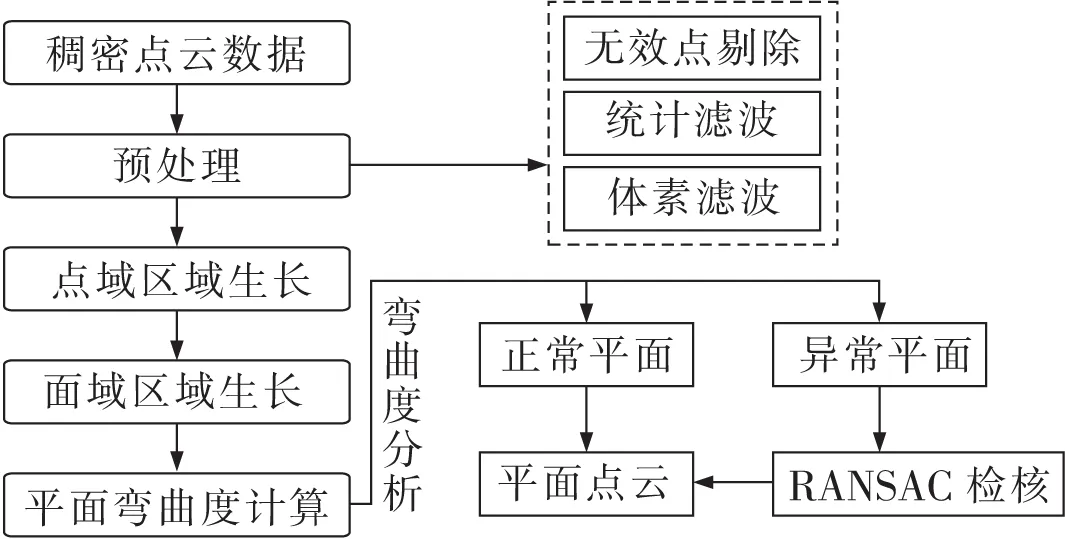
圖1 稠密點云平面分割技術路線Fig.1 Pipeline of plane segmentation for dense point cloud

1.2 數據預處理

由于稠密點云數據海量，對其直接處理，嚴重影響處理效率，因此在平面分割前對其進行預處理，為后續平面特征提取做準備。

首先對稠密點云數據P進行數據格式檢查，尋找數據中存在的“非法”格式，如點云中常見的“NAN”，并對其進行剔除。然后采用統計濾波濾除噪聲點，其原理如公式(1)所示。最后采用體素濾波，在保證點云數據整體輪廓的前提下，降低點云數據量，其中體素濾波采用邊長為l(0.02 m)的三維網格。在預處理后得到點云數據PV。

(1)

1.3 點域區域生長

在預處理后，以三維點為基礎，結合局部鄰域空間分析，制定鄰域生長條件，進行點域內的區域生長。主要包括以下步驟。

1)采用Kd-tree在PV中為所有三維點確定鄰域點集Gi={pk}。

2)構建鄰域協方差矩陣，采用特征值分解，計算其特征值λ1,λ2,λ3和對應特征向量ξ1,ξ2,ξ3(λ1>λ2>λ3)，ξ3作為該點法線，計算曲率V如下

(2)

3)根據曲率值V，對所有點升序排序。按曲率順序，依次遍歷每一點，并初始化種子隊列seeds，計算每一個種子點與各自鄰域點法線夾角。

4)若種子點法線與種子點法線夾角小于閾值?(3°)，則將當前鄰域點加入種子點seeds，若夾角大于?，繼續其他鄰域點計算。

5)若當前種子隊列均判斷完畢，則輸出當前平面點云plj。

6)遍歷PV所有點，直到所有點均已判斷完畢，見式(3)將PV分為剩余點云Ple、平面點云集{plj}。

(3)

式中n為平面數量。

1.4 面域區域生長

由于區域生長條件的限制，點域區域生長后的剩余點云Ple中仍包含部分屬于但未被歸類到相應平面結構的三維點。文中進一步采用面域區域生長進一步處理未分類的平面點。圖2為面域區域生長的示意，主要包括以下步驟。

1)平面篩選。瑣碎的平面點云，通常并非真正的實體結構，或對場景結構的表達的意義不大。因此如圖3所示，對于提取的平面點云，通過外接矩形面積近似作為平面點云面積，并經驗性地設置面積閾值s(0.02 m2)，剔除面積較小的平面，將其放回至剩余點云Ple中。

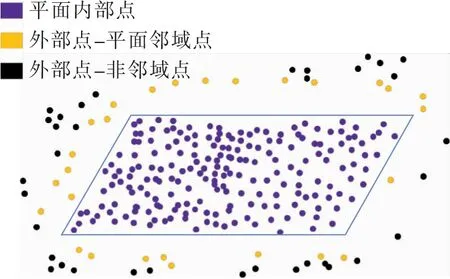
圖2 平面區域生長Fig.2 Planar region growing

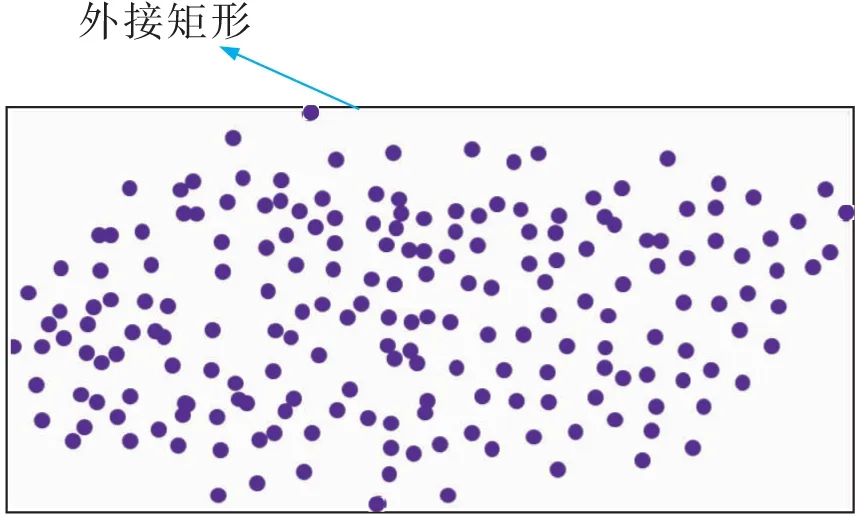
圖3 外接矩形Fig.3 Bounding rectangle

2)建立鄰域結構。以平面為基礎，再次采用KD-tree在剩余點云中，對平面點云建立鄰域結構，并去除重復的鄰域點(圖2中黃色點)。

3)平面生長。在每一個平面鄰域中，計算其到平面的距離，若小于距離閾值d1(0.03 m)，則將其歸類為當前平面點云。

1.5 平面彎曲度約束

平面分割后，以每一平面點云為基礎，計算平面的整體平均曲率，將其作為整個平面的彎曲度評價指標，主要包括以下步驟。

1)在公式(4)中，采用最小二乘法擬合平面方程，并計算整個平面點云重心點pc。

(4)

式中a1,…,a6為擬合的平面方程參數。

2)在公式(5)中，基于參數方程的一階、二階偏導、獲得pc處擬合曲面的第1基本量(E,F,G)和第2基本量(L,M,N)。

(5)

式中n為法向量。

3)在公式(6)中，結合參數方程計算出主曲率ρ1ρ2、平均曲率H。若重心點的平均曲率絕對值小于曲率閾值ε(0.4)，為正常平面，否則將其標注為彎曲度異常平面。

(6)

1.6 RANSAC檢核平面

平面彎曲度約束分析后，平面點云分為正常平面和彎曲度異常平面。如圖4在異常平面中采用RANSAC擬合平面點云方程，并計算整體平面的點云的誤差，將點到平面距離大于閾值d2(0.02 m)的點，作為粗差值點，進行剔除，提高平面分割準確度。而彎曲度正常平面則無需進行RANSAC檢測，可認為其已基本滿足幾何一致性原則，直接保存為最后的平面分割點云。最后輸出所有平面點云。

圖4 RANSAC檢核平面Fig.4 Check plane with RANSAC

2 實驗結果與分析

2.1 實驗數據與環境

實驗環境為Intel Core i7-5500U CPU@2.40 GHz 2.39 GHz，8.0 GB RAM，采用Ubuntu 16.04系統，C++編程實現。實驗采用4組數據，其中前2組數據來自PARK學者公布的公寓及閣樓場景點云數據[30]，后2組數據來自蘇黎世大學(UZH)的可視化與多媒體實驗室提供的辦公室掃描數據(https：//www.ifi.uzh.ch/en/vmml/research/datasets.html)。

圖5是采用文中預處理方法后的點云結果，體素濾波采用邊長為0.02m的三維體素網格進行體素化處理。從圖中預處理效果可以看出，在保持整體場景特征信息的前提下，點云數據量在一定程度上有所降低、大部分離群噪聲點得到有效剔除。

圖5 實驗數據Fig.5 Experimental data

2.2 平面分割對比實驗

在平面分割實驗中，選取傳統的區域生長和RANSAC方法作為對比實驗。各方法的分割效果如圖6所示，其中不同顏色表示不同平面點云。從圖中分割效果可以看出，RANSAC方法僅使用數學模型對點云進行分割，未能保證平面點云的連通性，致使多處不鄰的平面段誤識別為同一個平面點云。區域生長方法的分割效果總體較為良好，但平面分割受到生長條件的限制，未能保證平面的完整度，位于平面邊緣附近的點云未能很好進行歸類。目視效果上可見，文中方法可提取處場景中的大部分平面，同時平面之間的邊緣點云也得到良好歸類，平面結構的區分度較高，在保證準確度的同時也保證了平面結構的完整度。

圖6 平面分割對比Fig.6 Comparison of plane segmentation

2.3 未分類點分布

為進一步對比分析平面分割方法性能，如圖7提取出各方法分割后未歸類到具體平面的剩余點云。在剩余點分布方面，RANSAC方法由于僅采用空間數學模型，保留剩余點數量最少。其次是文中方法，最后是傳統區域生長方法。相比于區域生長方法，文中方法可以更好地處理平面邊緣點，減少剩余點數量，提高平面完整度。

圖7 未分類點分布Fig.7 Distribution of unclassified points

2.4 精度評估

進一步量化分析分割方法的性能，采用式(7)和式(8)中準確度(Corrrectness，Cr)、完整度(Completeness，Cm)[31]指標評估各算法。實驗中采用CloudCompare軟件的標記功能，勾選數據中的平面點并添加Label作為評估的真值。

(7)

(8)

式中TP為正確分割平面點;FP為錯誤識別的平面點;FN為漏檢的平面點。

表1記錄了實驗中3種分割方法在4個數據的分割結果的平面數量、剩余點數、準確度和完整度。其中RANSAC方法由于空間幾何模型在全局范圍提取平面，可提取出場景中的絕大部分平面點。但由于實驗數據中存在大量的平面，致使RANSAC方法所提取的大部分平面點是空間非連續的，這與空間平面的幾何屬性相矛盾。區域生長方法和文中方法所分割平面均由空間連續三維點構成，符合空間平面的幾何特性。同時相比于區域生長方法，文中方法在準確度與完整度方面均所有提升，4個場景中準確度均提升2%左右，均達到95%以上。完整度提高效果為：公寓場景提升約20%；閣樓場景提升約27%；辦公室1場景提升約12%；辦公室2場景提升約11%。文中方法更加魯棒地提取稠密點云中的平面結構，并提高平面特征的完整度。為后續場景建模以及機器人定位導航提高更加魯棒的特征結構。

表1 平面分割量化統計Table 1 Quantitative statistics of plane segmentation

3 結 論

1)利用點域內區域生長和面域內區域生長相結合，可以有效克服傳統區域生長在平面邊緣分割時的欠分割現象，平面分割的完整度提高約17%。

2)采用曲率值近似表達平面彎曲度，并對所分割的平面點云進行檢核，可以有效檢測出異常彎曲的平面，有利于檢測平面中的粗差點。

3)利用RANSAC檢核平面，可以在保證平面分割的連通性的基礎上，進一步提高平面分割的準確度，在典型的室內場景中，分割的準確度可達到95%。

4)基于稠密點云數據的平面分割方法可為基于平面結構的特征建模以及室內機器人導航定位提供可靠的特征基礎。