低復雜度自適應容積卡爾曼濾波算法

2022-04-29 06:35:18李春輝馬健楊永建甘軼

北京航空航天大學學報 2022年4期

李春輝，馬健，楊永建，甘軼

（空軍工程大學航空工程學院，西安 710038）

確定采樣型濾波算法估計精度高，實現簡單，是近年來非線性系統狀態估計領域的一個研究熱點，并廣泛應用于目標跟蹤、金融、信號處理和導航等領域［1］。確定采樣型濾波算法包括無跡卡爾曼濾波（unscented Kalman filter，UKF）［2］、中心差分卡爾曼濾波（central difference Kalman filter，CDKF）［3］及容積卡爾曼濾波（cubature Kalman filter，CKF）［4-5］，理論上已經證明，這些算法能至少以二階泰勒精度逼近各種非線性系統的后驗協方差和均值［6］，因此不僅具有比擴展卡爾曼濾波（extended Kalman filter，EKF）更高的濾波精度，還能克服EKF需要計算雅可比矩陣、強非線性時較差的數值穩定性等不足。相比于粒子濾波（particle filter，PF），確定采樣型濾波在計算量上具有很大優勢，而且不會出現 PF粒子退化和貧化問題［1］。

Arasaratnam和Haykin［4-5］利用球面徑向容積準則逼近最優估計的狀態后驗分布而提出的CKF算法，不僅能克服UKF在高維度和強非線性系統中的應用局限，同時具備更好的濾波精度及數值穩定性［7］。

在降低CKF算法復雜度方面，文獻［20］提出了一種簡化CKF算法，但是該算法對克服建模不確定性的提高并不大。文獻［17］將STF與假設檢驗理論結合以檢測不確定性，在運行時間上有很大優化，但是求解漸消因子的計算量仍然不可避免。

為了能使CKF算法具有對目標模型不匹配及狀態突變時的魯棒性，同時能夠避免強跟蹤CKF算法較大的計算量，提出了一種低復雜度自適應CKF算法。首先，設立了基于新息的自適應修正判決準則及修正方式，然后，對系統狀態預測值進行基于新息的直接補償修正，使得濾波算法能夠及時“跟上”目標真實狀態，進而減小濾波誤差。本文算法具有良好的濾波性能，同時在算法復雜度和仿真運行時間上有明顯改善。

1 容積卡爾曼濾波

對目標建模時考慮如下非線性離散加性噪聲系統：

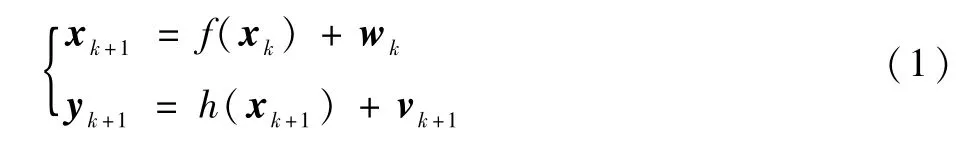
式中：f和h分別為非線性的狀態轉移函數和量測函數；xk+1∈Rnx和yk+1∈Rny分別為系統狀態向量和量測向量；wk和vk+1分別為系統過程噪聲和量測噪聲，兩者是相互獨立的零均值白噪聲且對應的協方差矩陣分別為Qk和Rk。系統初始狀態為x0～N（0，P0），與wk、vk+1互不相關，P0為初始協方差矩陣。

CKF算法采用球面徑向容積規則來逼近最優框架中的狀態后驗均值和后驗協方差，根據文獻［5，11］，將CKF算法流程總結如下。

1.1 時間更新

1.2 量測更新

2 自適應修正容積卡爾曼濾波

2.1 誤差分析

2.2 基于新息的自適應修正判決準則和修正方式

由2.1節的分析可知，當目標模型不匹配或者目標狀態發生突變時，新息ek+1能反映系統狀態預測值和量測預測值出現的較大偏差，同時也能反映出預測值偏離實際狀態的“趨勢”和“程度”。因此，基于新息來判決是否修正及如何修正。

圖1 基于新息的修正判決準則Fig.1 Amending judgment criteria based on innovation sequence

修正系數的選取首先要遵循避免過度修正基本原則，其次主要考慮兩方面：一是修正系數與系統量測精度相關；二是新息ek+1所提供的信息維度，如假設新息中只含有位置的信息，則在選取時c1或c3可以選取得稍大些，速度的修正可以通過位置變化來傳遞，但是對應的系數c2或c4選取得稍小些。

2.3 低復雜度自適應CKF算法實現

根據建立的判決準則和修正方式總結了本文算法的流程，如圖2所示。圖中在判別之后的虛線是低復雜度自適應CKF算法的路徑，實線是標準CKF算法的路徑，具體步驟總結如下：

圖2 低復雜度自適應CKF算法流程Fig.2 Flowchart of low-complexity adaptive CKF algorithm

步驟1 通過式（2）～式（12）完成時間更新及量測更新的一部分，并得到新息ek+1。

步驟2 將新息中對應變量的絕對值與門限進行比較，若滿足修正判決條件，則用式（18）進行狀態預測值修正，之后用式（9）～式（17）完成濾波，并用式（19）進行預測誤差協方差補償。

步驟3 若不需要進行修正，則按式（13）～式（17）完成標準CKF濾波。

步驟4 重復步驟1～步驟3。

3 算法復雜度分析

使用浮點操作數（flops）來分析算法復雜度是直觀有效的方法，根據文獻［21-22］，定義以下4種矩陣運算的flops：

1）矩陣加減法。A∈Rn×m，B∈Rn×m，A±B運算的復雜度為nm flops。

2）矩陣乘法。A∈Rn×m，B∈Rm×l，AB運算的復雜度為2nm l-nl flops。

3）矩陣求逆。A∈Rn×n，A-1運算的復雜度為n flops。

4）Cholesky分解。A∈Rn×n，chol（A）運算的復雜度為n3／3 flops。

假設系統狀態變量為n維，量測變量為l維，則利用上述矩陣運算復雜度定義，對標準CKF算法、強跟蹤CKF算法［13］及本文提出的低復雜度自適應CKF算法的復雜度進行計算，結果如表1所示。

表1 三種算法復雜度計算結果Table 1 Computational results of complexity of three algorithms

CKF算法的復雜度分析具體過程可見文獻［21］，參照該過程得到了其他2種算法的復雜度計算結果。

強跟蹤CKF算法主要考慮文獻［13］中式（3）、式（6）、式（10）和式（11）求解漸消因子上，4個公式對應的算法復雜度依次為2 l、2 l2、2n3+6n2l+2 l2n+l2-3nl和2 l2flops。

低復雜度自適應CKF算法主要考慮式（12）新息的計算及式（18）和式（19）的計算，對應步驟的算法復雜度依次為l、n和n2+l flops。

盡管文獻［13］中的強跟蹤CKF算法已經進行了改進，求解時避免了計算雅可比矩陣，但是相比而言，本文算法在復雜度上仍有明顯改善。將強跟蹤CKF算法與低復雜度自適應CKF算法的復雜度求差可得Δflops＝n（2n2-n-1）+3nl（2n-1）+2 l2n+5 l2，在n和l都大于1時，這一差值會隨著n和l的增大而變大，即隨著狀態向量、量測向量維度的增加，低復雜度自適應CKF算法的優勢會更大。為了更直觀地體現這一差異，根據得到的算法復雜度公式繪制了3種算法的復雜度隨狀態向量、量測向量維度分別變化時的曲線，如圖3和圖4所示。

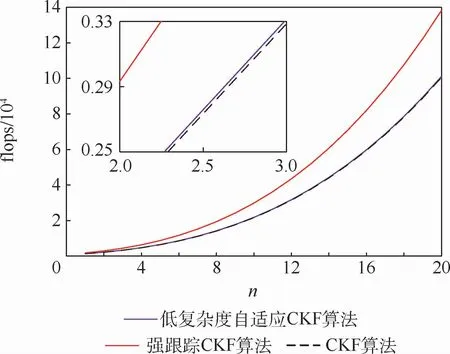
圖3 三種算法的復雜度比較（l＝8）Fig.3 Comparison of three algorithms complexity（l＝8）

圖4 三種算法的復雜度比較（n＝8）Fig.4 Comparison of three algorithms complexity（n＝8）

4 仿真與分析

4.1 建模與仿真條件設置

仿真中，目標運動模型為勻速運動和勻速轉彎運動的混合機動。系統狀態向量為X＝［x，˙x，y，˙y］T，其中勻速運動模型的狀態轉移矩陣為FCV，勻速轉彎運動模型的狀態轉移矩陣為FCT，分別如下：

為了驗證低復雜度自適應CKF算法在目標建模不匹配時的濾波性能，在跟蹤時與CKF算法、強跟蹤CKF算法進行對比，同時3種算法在目標建模時都僅使用勻速運動模型FCV。

在目標運動仿真參數的設置上，轉彎率ω＝5°／s，采樣時間T＝1 s，目標在0～250 s的時間內保持交替變換運動狀態，其中勻速直線運動時間段為［0，70］s，（120，145］s，（160，200］s，（225，250］s；勻速轉彎運動時間段為（70，120］s，（145，160］s，（200，225］s，共3次轉彎。

目標初始狀態為x0＝［1 000 m，200 m／s，1 000 m，10 m／s］T，系統初始協方差P0＝diag（3，1，3，1）；系統過程噪聲協方差矩陣Q＝diag（1，1，1，1），量測噪聲協方差矩陣R＝diag（100，100）；強跟蹤CKF算法的遺忘因子取0.95。

仿真結果以目標x軸和y軸位置上的均方根誤差（root mean square error，RMSE）來評價，并進行150次蒙特卡羅仿真，均方根誤差的定義為

4.2 仿真結果分析

圖5為其中一次蒙特卡羅仿真的目標真實運動軌跡及3種算法的濾波軌跡。可以看到，低復雜度自適應CKF算法及強跟蹤CKF算法均能很好地跟蹤目標，但是由于濾波建模時使用的始終是勻速運動模型，CKF算法在3次機動轉彎時跟蹤性能就會下降。

圖6和圖7分別為濾波階段x軸和y軸位置的均方根誤差，左上角為對10～20 s階段放大顯示。可以看出，整體上低復雜度自適應CKF算法及強跟蹤CKF算法能夠在建模不準確時始終保持較高的濾波精度，但是CKF算法只有在目標勻速運動階段即建模匹配時才能發揮很好的濾波性能，在目標轉彎階段時其濾波精度受到很大影響。但是從圖6和圖7中放大顯示部分來看，CKF算法在目標運動建模準確時濾波精度要比另外2種算法要高。

表2為3種算法在濾波時間段里的平均均方根誤差。結合其中的數據及圖6和圖7可以看出，低復雜度自適應CKF算法能夠保持和強跟蹤CKF算法基本一致的濾波精度，可以較好地克服由于目標建模不準確或者目標狀態突變帶來的不利影響。

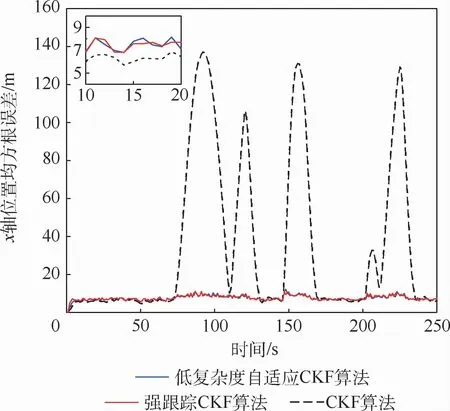
圖6 x軸位置均方根誤差Fig.6 RMSE of position in x axis

圖7 y軸位置均方根誤差Fig.7 RMSE of position in y axis

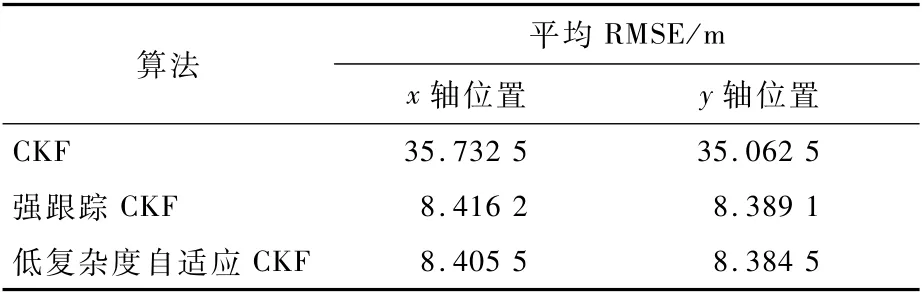
表2 不同算法平均均方根誤差對比Table 2 Comparison of mean RMSE among different algorithms

在硬件配置為Intel i7 4710處理器和4 GB內存的筆記本電腦上使用MATLAB 2017a進行了試驗。3種算法的單次仿真平均運行時間和運行時間增加百分比如表3所示。運行時間增量計算方式為（Ti-T0）／T0，T0為CKF算法的運行時間，Ti為其他2種算法的運行時間。

由表3可見，CKF算法耗時最短，低復雜度自適應CKF算法在運行時間上略微增加了1.29%，而強跟蹤CKF算法由于需要求解漸消因子，耗時最多，相比較CKF算法增加了29.53%。運行時間對比數據和前文算法復雜度計算結果相吻合。

表3 不同算法運行時間對比Table 3 Comparison of running time among different algorithms

為了驗證低復雜度自適應CKF算法的濾波數值穩定性，繪制3種算法每次蒙特卡羅仿真中x軸和y軸位置的平均均方根誤差，如圖8和圖9所示。可以看出，低復雜度自適應CKF算法及強跟蹤CKF算法每次仿真中的位置平均均方根誤差都低于CKF算法，這是因為CKF算法在每次仿真中目標建模不匹配即轉彎階段時的濾波誤差會劇增。同時相比于CKF算法，另外2種算法的位置平均均方根誤差沒有出現某次仿真發散的情況，而且曲線波動幅度更小，數值穩定性更優。