基于混合生成網絡的軟件系統異常狀態評估

2022-05-06 06:06:36楊宏宇李譯張良

湖南大學學報(自然科學版) 2022年4期

楊宏宇，李譯，張良

（1.中國民航大學安全科學與工程學院，天津 300300；2.中國民航大學計算機科學與技術學院，天津 300300；3.亞利桑那大學信息學院，圖森美國AZ 85721）

軟件系統作為社會生產方式和信息化發展的成果之一，正朝著復雜化的方向不斷發展，系統一旦產生異常［1］，將對軟件系統的安全穩定運行造成影響［2］.為克服軟件系統異常解決方案中存在的盲目性和被動性，需要對軟件系統進行及時、有效的狀態評估.軟件系統異常狀態評估是從異常的角度對系統狀態進行評估，分析異常事件對系統造成的危害程度，為制定科學合理的軟件系統安全保障方案提供客觀依據和基礎支持.

現有系統狀態評估方法主要包括基于數學模型、基于邏輯規則推理和基于神經網絡的方法［3-5］.基于數學模型的狀態評估方法通過對影響系統正常運行的因素進行分析，建立影響系統運行因素與系統狀態之間的對應關系.由于易受主觀因素影響且實時性較差，基于數學模型的評估方法的評估結果不夠理想，與實際情況偏差較大［6-7］.基于邏輯規則推理的狀態評估方法根據先驗知識構建模型并使用邏輯規則推理方法對系統狀態進行評估，憑借先驗知識對狀態指標設置閾值判斷系統狀態，使得評估結果主觀性強［8-9］.此外，由于軟件系統運行過程中產生的狀態信息量較大，基于邏輯規則推理的狀態評估方法適應性較差.與基于數學模型和基于邏輯規則推理的狀態評估方法相比，基于神經網絡的狀態評估方法由于具有高效和易拓展等特點應用更加廣泛，該類方法利用訓練數據集對特定模型進行訓練后可以對系統狀態進行分類，實現對系統狀態的評估［10-12］，常用的方法包括AVE［13］、深度挖掘［14］、卷積神經網絡［15］等.基于神經網絡的狀態評估方法雖然對系統狀態的評估效果較好，但該類方法的通用性和可擴展性較差，對系統狀態的量化分類效果不佳.

針對上述問題，本文提出一種基于混合生成網絡的軟件系統異常狀態評估方法.首先，通過對長短期記憶網絡（long short-term memory network，LSTM）和變分自動編碼器（variational auto-encoder，VAE）的融合，設計一個LSTM-VAE 混合生成網絡，以此為基礎構建一種基于LSTM-VAE混合生成網絡的系統異常狀態檢測模型.然后，采集系統關鍵特征參數數據，利用建立的LSTM-VAE異常狀態檢測模型對關鍵特征參數進行檢測并獲取其相應的異常度量值.最后，利用耦合度方法［16］對線性加權和方法進行優化，根據優化后得到的加權耦合度方法計算系統異常狀態的量化值，實現對軟件系統異常狀態的量化評估.

1 軟件系統異常狀態評估方法

1.1 方法設計

基于混合生成網絡的軟件系統異常狀態評估由基于長短期記憶網絡-變分自動編碼器（LSTMVAE）的系統異常狀態檢測模型（簡稱LSTM-VAE 異常檢測模型）構建和系統異常狀態評估兩部分組成，如圖1 所示.LSTM-VAE 異常檢測模型構建為系統異常狀態評估提供系統異常狀態檢測模型、異常閾值和最大重構誤差；系統異常狀態評估利用已構建完成的異常檢測模型獲取系統關鍵特征參數的異常度量值，然后通過加權耦合度方法對系統異常狀態的量化值進行計算，根據系統異常狀態的量化值實現軟件系統異常狀態評估.本文方法中兩個部分的處理過程設計如下：

圖1 軟件系統異常狀態評估方法Fig.1 Software system abnormal status evaluation method

1.1.1 基于LSTM-VAE 的系統異常狀態檢測模型構建

首先，篩選出系統正常運行時序的關鍵特征參數歷史時序數據，輸入LSTM-VAE 混合生成網絡中進行訓練，由訓練完成后的LSTM-VAE 混合生成網絡獲取系統正常運行狀態下的關鍵特征參數時序數據的長短期依賴關系和分布形式.

然后，將含有異常標注的關鍵特征參數的歷史時序數據輸入LSTM-VAE 混合生成網絡中，獲取系統關鍵特征參數的重構誤差，此時的重構誤差表示關鍵特征參數偏離正常狀態數據的分布程度.

最后，利用標注的異常信息與模型檢測結果統計模型準確率與召回率，選擇準確率等于召回率時的閾值為異常閾值，選擇重構誤差中最大的數值為最大重構誤差.其中，異常閾值為該關鍵特征參數偏離正常狀態下數據分布程度的下限，用于判斷系統關鍵特征參數是否異常，最大重構誤差為關鍵特征參數偏離正常狀態下數據分布程度的上限.

1.1.2 系統異常狀態評估

首先，采集系統關鍵特征參數的時序數據，利用已構建的LSTM-VAE 異常檢測模型對采集到的系統關鍵特征參數時序數據進行檢測，獲取系統各關鍵特征參數的異常度量值.

然后，依據AHP 的權重評定原則，采用1-9 標度法［17］確定系統各關鍵特征參數的相對重要度，對系統各關鍵特征參數進行權重賦值.

最后，利用加權耦合度方法計算系統異常狀態的量化值，實現軟件系統異常狀態評估.

1.2 LSTM 與GRU的對比分析

目前，采用門控機制的神經網絡模型主要包括長短期記憶網絡（LSTM）和門控循環單元（gated re?current unit，GRU），LSTM 和GRU 的特點對比如表1所示.LSTM 和GRU 均是作為長、短期記憶的解決方案而提出的，兩者都具有稱為門的內部機制.不同之處在于：LSTM 具有3個門控單元，而GRU 相比LSTM少了一個門控單元，故從計算角度來看，GRU結構簡單，效率更高.但是在數據集較大的情況下，與GRU相比，LSTM具有更強的表征能力［18］.

表1 LSTM 與GRU的比較Tab.1 Comparison of LSTM and GRU

本文的研究是在數據集較大的場景下開展的，故選擇使用LSTM.雖然LSTM 犧牲了部分時間及計算的簡便性，但LSTM對關鍵特征參數的表征能力更強也更靈活，對大數據環境的適應性更好.

2 基于混合生成網絡的系統異常狀態檢測模型

2.1 變分自動編碼器和長短期記憶網絡

VAE 的基本結構如圖2 所示.作為經典的無監督異常檢測方法，VAE 在模型訓練時無須大量標注數據，可通過辨識輸入數據與重構輸出數據間的差異來達到異常檢測的目的.首先，由編碼器對輸入樣本X=｛xk|k=1，2，…，n｝中的元素Xk進行擬合，使其服從均值為u和方差為σ的正態分布.然后，通過對所得正態分布進行采樣得到隱變量Z=｛zk|k=1，2，…，n｝，其中，元素Zk服從均值為0 和方差為1 的標準正態分布.最后，由解碼器對隱變量Z進行解碼，生成輸出樣本Y=｛yk|k=1，2，…，n｝，通過計算X與Y之間的均方誤差獲得輸入樣本與輸出樣本之間的重構誤差：

圖2 VAE基本結構Fig.2 Structure of VAE

LSTM 通過記憶單元和門機制提取時序數據內部的長短期依賴關系，其神經元結構如圖3 所示.LSTM 的遺忘門和輸入門控制單元Ct的輸入，輸出門控制單元Ct的輸出.其中，遺忘門和輸入門分別控制上一時刻的狀態Ct-1和當前時刻的狀態輸入記憶單元Ct中，輸出門控制當前記憶單元Ct輸入當前時刻的輸出ht中.

圖3 LSTM神經元結構Fig.3 Structure of LSTM neurons

由上文分析可知，VAE和LSTM分別具有鮮明的特點，如表2 所示.VAE 的訓練無須大量標注數據并且采樣過程具有隨機性，有助于提高模型的泛化能力.但是，VAE 對系統時序數據的時序特征不敏感，無法獲取并表征系統時序數據內部的長短期依賴關系.由于系統關鍵特征參數數據具備明顯的時序特征，LSTM 可以通過遺忘門、輸入門和輸出門控制記憶單元的狀態，使其能夠獲取并表征系統時序數據內部的長短期依賴關系.

表2 VAE和LSTM 的特點Tab.2 Characteristic of VAE and LSTM

2.2 基于LSTM-VAE的混合生成網絡設計

為解決現有異常檢測方法在訓練過程中需要大量標注數據和缺少對時序數據內部長短期依賴關系關注的問題，本文將LSTM 與VAE 融合，設計一個LSTM-VAE 網絡（圖4）.在該網絡中，用LSTM神經元對VAE 的編碼層和解碼層中的神經元進行替換，即采用LSTM 對輸入時序數據內部的長短期依賴關系進行提取，通過VAE 的變分推理對系統時序數據的分布進行建模.

圖4 LSTM-VAE網絡結構Fig.4 Structure of LSTM-VAE network

與單一的LSTM 或VAE 相比，LSTM-VAE 網絡可以對系統關鍵特征參數時序數據的長短期依賴關系進行提取，無須大量標注的關鍵特征參數數據訓練模型，同時模型在隱變量學習過程中利用采樣的隨機性起到正則化作用，可以防止網絡過擬合，使得LSTM-VAE 混合生成網絡在提取時序數據特征和提高模型泛化能力方面更具優勢.

2.3 基于混合生成網絡的系統異常狀態檢測模型構建

以本文設計的LSTM-VAE 混合生成網絡為基礎，構建一個系統異常狀態檢測模型.該異常檢測模型的構建步驟設計如下.

輸入：系統關鍵特征參數的歷史時序數據.

輸出：異常檢測模型.

步驟1：選取與系統狀態相關的關鍵特征參數.

選擇系統CPU 利用率、內存利用率、磁盤利用率和網卡吞吐率等特征參數作為系統狀態異常檢測和評估系統異常狀態的關鍵特征參數，獲取系統各關鍵特征參數的歷史時序數據.

步驟2：系統關鍵特征參數預處理.

對系統關鍵特征參數進行歸一化處理，抑制取值范圍差異對訓練產生的負面影響，

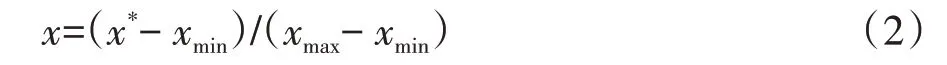
式中：x表示經過歸一化之后的關鍵特征參數值，x*表示初始關鍵特征參數值，xmax表示關鍵特征參數中的最大值，xmin表示關鍵特征參數中的最小值.

步驟3：數據集劃分.

將系統關鍵特征參數歷史時序數據劃分為訓練集與測試集，訓練集中不含異常標簽的數據，測試集中含有異常標簽的數據.

步驟4：模型訓練.

利用訓練集對LSTM-VAE 混合生成網絡進行訓練.采取滑動時間窗口法對關鍵特征參數的訓練集序列進行子序列提取，假設時間窗口長度為l，關鍵特征參數序列長度為L，則可以從中提取L-l+1 個子序列.假設｛x1，x2，…，xl｝為系統CPU 利用率訓練集中部分運行數據序列片段，其中，xi為i時刻系統CPU利用率，l為序列片段長度，LSTM-VAE 混合生成網絡對｛x1，x2，…，xl｝進行網絡重構后的輸出序列為｛y1，y2，…，yl｝，采用均方根誤差函數計算得到輸入序列｛x1，x2，…，xl｝與重構輸出序列｛y1，y2，…，yl｝之間的重構誤差e

由混合生成網絡輸出的重構誤差集合E為

式中：m=L-l+1，m為CPU 利用率訓練集中數據序列片段個數，L為CPU 利用率訓練集中數據序列長度，l為序列片段長度也即滑動時間窗口長度.

同樣地，采用相同方法，得到系統的內存利用率、磁盤利用率和網卡吞吐率等關鍵特征參數的重構訓練誤差集合.當關鍵特征參數重構訓練誤差集合的所有重構誤差均達到設定的精度要求或模型達到設定的迭代次數時，結束訓練.

步驟5：異常閾值選擇與最大重構誤差.

將含有標簽的系統各關鍵特征參數測試集輸入已訓練完成的LSTM-VAE 異常檢測模型中.｛X1，X2，…，XL｝為系統CPU 利用率測試集中部分運行數據序列片段，其對應的標注信息序列片段為｛B1，B2，…，BL｝，其中，Xi為i時刻系統CPU 利用率數值，Bi為測試集中對應序列Xi的標注信息（Bi=1 表示i時刻該系統CPU 利用率數值異常，Bi=0 表示該時刻系統CPU利用率數值無異常），L為序列片段長度.

首先，將CPU 利用率測試集數據輸入訓練完成后的LSTM-VAE 異常檢測模型中獲取相應的重構輸出序列，由公式（3）和公式（4）計算得到該關鍵特征參數測試集的重構誤差集合Ecpu=｛e1，e2，…，em｝.

然后，定義CPU 利用率閾值ζ，將CPU 利用率測試集重構誤差集合Ecpu中第i個數據序列片段的重構誤差ei與CPU 利用率閾值ζ進行比較，若ei＜ζ，則表示異常檢測模型判定該序列片段無異常，用Ci=0 表示；若ei≥ζ，則表示異常檢測模型判定該序列片段異常，用Ci=1 表示.為評估模型性能，引入準確率和召回率指標.

準確率P：CPU利用率測試集中檢測為異常的序列片段中標注為異常的序列片段的比例.

召回率R：CPU利用率測試集中標注為異常的序列中檢測為異常的序列片段的比例.

最后，由準確率P和召回率R的定義可知，準確率P隨閾值ζ的增大而增大，召回率R隨閾值ζ增大而減小.當準確率P等于召回率R時，模型性能最佳.因此，定義此時的閾值ζ為CPU 利用率的異常閾值ζ*，其中，CPU 利用率的異常閾值ζ*表示該關鍵特征參數偏離正常狀態下數據分布程度的下限.同時，定義該關鍵特征參數的最大重構誤差ecpu為

式中：ecpu為CPU 利用率的最大重構誤差，表示該關鍵特征參數偏離正常狀態下數據分布程度的上限.

同樣地，采用相同方法，得到系統的內存利用率、磁盤利用率和網卡吞吐率等關鍵特征參數的異常閾值和最大重構誤差.

3 系統異常狀態評估

在完成LSTM-VAE 異常檢測模型構建并獲得系統各關鍵特征參數的異常閾值和最大重構誤差后，將系統各關鍵特征參數的時序數據輸入LSTM-VAE異常檢測模型中，獲取系統各關鍵特征參數的異常度量值.然后對系統各關鍵特征參數的權重進行賦值.最后利用耦合度方法對線性加權和方法進行優化，通過加權耦合度優化方法計算得到系統異常狀態值.

系統異常狀態評估部分的具體步驟設計如下：

輸入：各關鍵特征參數的時序數據.

輸出：系統異常狀態值.

步驟1：獲取各關鍵特征參數的異常度量值.

將系統關鍵特征參數時序數據輸入LSTM-VAE異常檢測模型中，計算輸入序列與輸出序列之間的重構誤差.當重構誤差小于異常閾值時，重新獲取時序數據進行異常檢測；否則，判斷該關鍵特征參數為異常.然后，基于已獲得的重構誤差、異常閾值與最大重構誤差，計算該關鍵特征參數的異常度量值

式中：Ii為系統第i個關鍵特征參數的異常度量值，ei為該關鍵特征參數此時的重構誤差，為系統第i個關鍵特征參數的異常閾值，emax為系統第i個關鍵特征參數的最大重構誤差.

步驟2：各關鍵特征參數權重賦值.

依據AHP 的權重評定原則，采用1-9 標度法確定系統各關鍵特征參數的相對重要度，構造決策矩陣M=（mij）n×n，決策矩陣M為

式中：n為系統關鍵特征參數的個數，元素mij表示第i個關鍵特征參數與第j個關鍵特征參數的重要程度之比，當i=j時，mij=1.

計算決策矩陣M的最大特征根λmax及其特征向量W=（w1，w2…，wn），

最大特征值λmax對應的特征向量W即為各關鍵特征參數的權重集合（w1，w2…，wn）.

步驟3：改進加權耦合度方法計算系統異常狀態值.

線性加權和方法僅強調變量之間的獨立性，不考慮變量間數值差異與相互作用問題，耦合度方法常用于表示變量間數值差異與相互作用.軟件系統作為一個整體，其不同組件及關鍵特征參數之間的相互作用可能影響系統的正常運行.忽略不同組件及關鍵特征參數之間的差異和相互作用將導致系統狀態評估時結果出現較大的差異.因此，本文在線性加權和方法的基礎上融入耦合度方法計算系統異常狀態值，即在量化系統異常狀態時關注不同關鍵特征參數異常度量值間的差異給量化結果帶來的影響.

首先，基于步驟1 獲取的系統各關鍵特征參數的異常度量值Ii，計算系統耦合度H

然后，利用系統各關鍵特征參數權重wi和系統各關鍵特征參數的異常度量值Ii，計算系統關鍵特征參數異常度量值的線性加權和S

最后，基于系統耦合度H和系統關鍵特征參數異常度量值的線性加權和S，計算系統異常狀態值Sa

其中，系統耦合度H與系統關鍵特征參數異常度量值的線性加權和S的值均在［0，1］范圍內.

根據指數函數的定義可知，式（13）在［0，1］范圍內為單調遞減函數，在S一定的條件下，H越小，則Sa越大；同樣地，在H一定的條件下，S越大，則Sa越大.因此，根據該方法計算得到的系統異常狀態量化結果符合本文的評估思路，即在計算系統異常狀態值時關注不同特征參數的異常度量值之間的差異對評估結果造成的影響.

4 實驗與結果分析

4.1 實驗數據

實驗數據集采用百度公司聯合清華大學公開的運維數據集，選擇其中的CPU 利用率、內存利用率、磁盤利用率與網卡吞吐率這四項關鍵特征參數進行異常檢測驗證實驗.數據集中每個關鍵特征參數均包含連續4 周的數據，時間間隔為5 min.在實驗中，將各關鍵特征參數的前三周數據劃分為訓練集，將最后一周數據劃分為測試集，其中，訓練集中數據均為系統正常運行時序數據且無異常數據，測試集中含有異常數據且異常數據已經標注.部分關鍵特征參數的數據格式如表3所示.

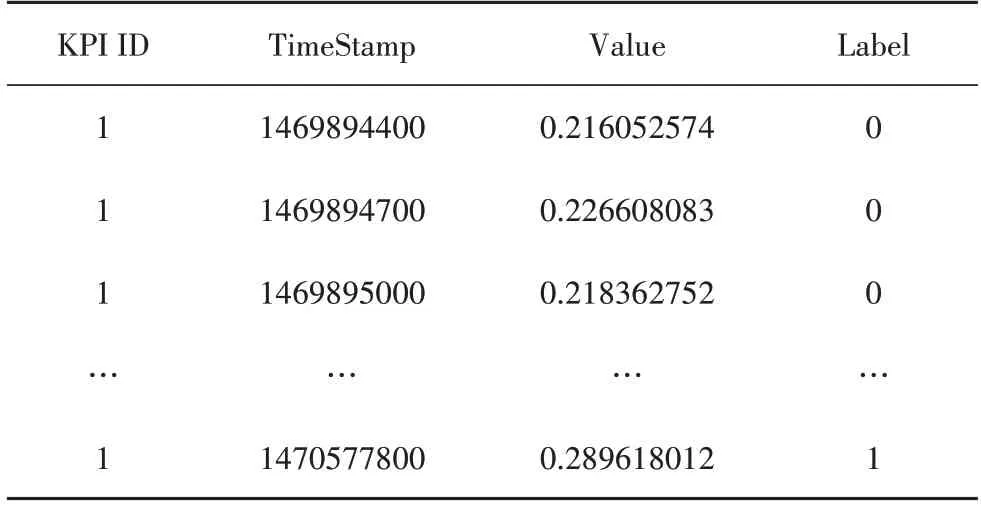
表3 關鍵特征參數數據格式Tab.3 Data formats for key feature parameters

4.2 LSTM-VAE混合生成網絡配置及模型訓練

LSTM-VAE混合生成網絡由LSTM和VAE構成，輸入向量維數等于輸出向量維數，具體網絡的配置如表4所示.

表4 LSTM-VAE網絡配置Tab.4 Configuration of LSTM-VAE network

在訓練過程中，各關鍵特征參數的訓練誤差與迭代次數關系如圖5 所示.由圖5 可見，各關鍵特征參數的訓練誤差隨著迭代次數的增加而迅速減小.其中，各關鍵特征參數的誤差曲線在經過35 次迭代后趨于平穩，表明模型達到較好的收斂效果，能夠對系統正常的關鍵特征參數時序數據的長短期依賴關系和數據分布形式進行學習并實現數據重構.

圖5 訓練誤差與迭代次數Fig.5 Diagram of training error and number of iterations

4.3 異常閾值選擇與評估效果

在實驗中，通過遍歷所有的可取閾值，確定異常閾值.可取閾值范圍為0 到該關鍵特征參數的最大重構誤差.設置初始閾值為0，若關鍵特征參數的重構誤差大于0，將其視為異常；否則，首先計算閾值為0時的準確率和召回率，然后增加閾值并計算對應的準確率和召回率，當閾值設置為該關鍵特征參數的最大重構誤差時結束.利用訓練完成后的LSTMVAE 異常檢測模型對系統各關鍵特征參數的測試集進行異常檢測，得到相應的閾值與準確率、召回率的變化關系，如圖6所示.

由圖6 可見，當CPU 利用率的異常閾值為0.102時，CPU 利用率的準確率與召回率相等，因此選擇CPU 利用率的異常閾值為0.102；當內存利用率的異常閾值為0.088時，內存利用率的準確率與召回率相等，因此選擇內存利用率的異常閾值為0.088；當磁盤利用率的異常閾值為0.190時，磁盤利用率的準確率與召回率相等，因此選擇磁盤利用率的異常閾值為0.190；當網卡吞吐率的異常閾值為0.122 時，網卡吞吐率的準確率與召回率相等，因此選擇網卡吞吐率的異常閾值為0.122.

圖6 各關鍵特征參數的閾值與準確率、召回率關系圖Fig.6 Diagram of relationship between threshold values and accuracy rate，recall rate

基于系統各關鍵特征參數測試集，計算得到各關鍵特征參數對應的最大重構誤差，結果如表5所示.

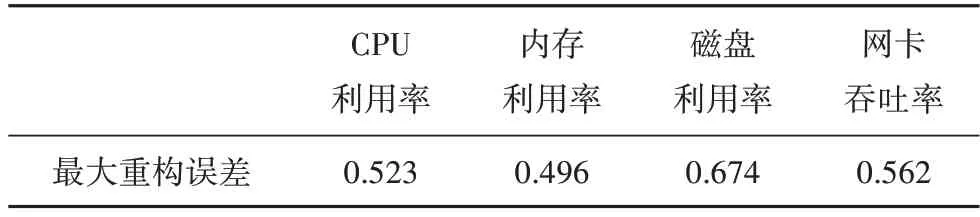
表5 各關鍵特征參數的最大重構誤差Tab.5 Maximum reconstruction error of each key feature parameter

為評價本文異常檢測模型的效果，分別采用VAE、AE、LSTM-AE 和LSTM-VAE 網絡得到不同關鍵特征參數評估的F1-score 值，F1-score=（2×P×R）/（P+R）.各模型的F1-score值如表6所示.

表6 不同網絡在不同關鍵特征參數測試集中的F1-score值Tab.6 F1-score values of different models in different key feature parameter test sets

由表6 可見，針對測試集中的CPU 利用率、內存利用率、磁盤利用率和網卡吞吐率4 個關鍵特征參數測試數據，LSTM-VAE 網絡模型的F1-score 值均優于其他模型.與VAE、AE 模型相比，LSTM-VAE 模型利用LSTM神經網絡的時序特征提取能力，能夠有效挖掘關鍵特征參數時序數據內部的長短期依賴關系，顯著提升異常檢測精度；同時，LSTM-VAE 網絡可以利用VAE的隱變量空間，減少LSTM-AE網絡中神經網絡的過擬合對異常檢測效果的影響，也有助于提升異常檢測效果.

4.4 滑動時間窗口長度確定

由于滑動時間窗口長度L的取值會影響LSTMVAE 模型的異常檢測效果，為了驗證滑動時間窗口長度對LSTM-VAE 模型的異常檢測效果的影響并確定最佳的滑動時間窗口長度值，有必要進行滑動時間窗口長度影響實驗.

在實驗中，選取不同窗口長度L的值并計算其對應的F1-score 值，選擇窗口長度值從長度4 到20依次增加2個單位長度進行實驗.選擇最高F1-score值所對應的窗口長度作為LSTM-VAE 模型的滑動時間窗口長度L的值，不同滑動時間窗口長度L與對應的F1-score值如圖7所示.

由圖7 可見，當滑動時間窗口長度L為12 時，LSTM-VAE 模型對各關鍵特征參數測試數據的F1-score 值均大于其他滑動時間窗口長度對應的F1-score 值，表明滑動時間窗口長度為12 時，LSTMVAE 模型對系統狀態的異常檢測效果最佳，所以，在LSTM-VAE 模型中，將滑動時間窗口長度L的值設定為12.

圖7 滑動時間窗口長度與F1-score值Fig.7 Sliding time window lengths and the corresponding F1-score values

4.5 異常狀態評估

4.5.1 關鍵特征參數異常度量值與關鍵特征參數賦權

在確定系統各關鍵特征參數的異常閾值和最大重構誤差后，為保證實驗結果具有可比性，選取10組關鍵特征參數異常時序數據組成測試集，用本文模型的方法對該數據集進行檢測并計算關鍵特征參數的重構誤差，由公式（7）計算測試集中關鍵特征參數的異常度量值，由公式（11）計算各測試集的系統耦合度，測試集中各關鍵特征參數的異常度量值如圖8 所示，測試集中各關鍵特征參數的系統耦合度如圖9所示.

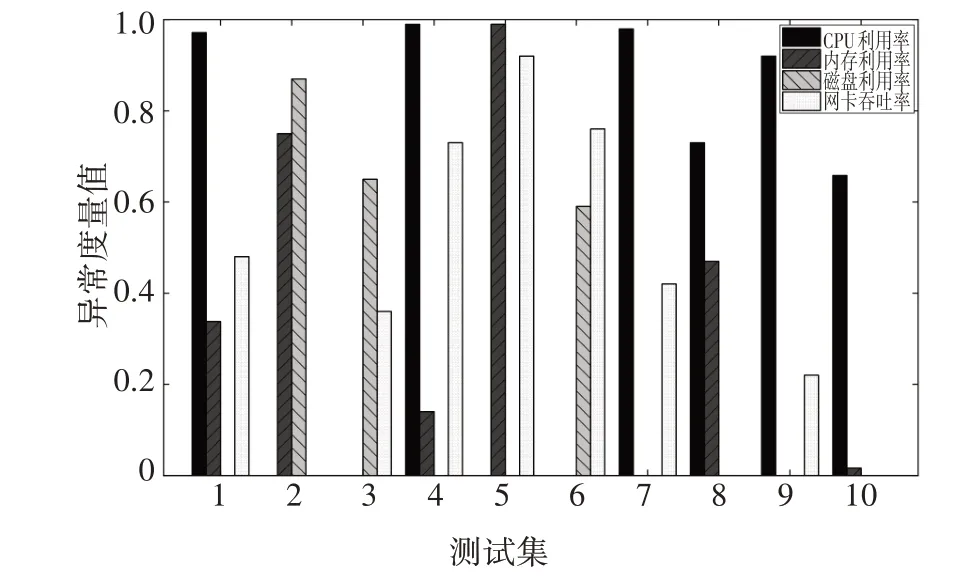
圖8 測試集中各關鍵特征參數的異常度量值Fig.8 Key feature parameters anomaly metric value in the test group

圖9 各測試集的系統耦合度Fig.9 System coupling degree of each test group

采用加權耦合度方法計算系統異常狀態值時，需要對系統各關鍵特征參數進行賦權.利用AHP 方法對系統關鍵特征參數進行主觀賦權，根據AHP 權重評定原則，采用1-9 標度法確定系統各關鍵特征參數的相對重要度，建立決策矩陣如表7所示.

表7 決策矩陣Tab.7 Decision matrix

計算得到決策矩陣的最大特征根及其對應的特征向量，如表8所示.

表8 最大特征值及其特征向量Tab.8 Maximum eigenvalue and its eigenvector

由表8 可見，CPU 利用率權重為0.443 5，內存利用率權重為0.312 1，磁盤利用率權重為0.122 2，網卡吞吐率權重為0.122 2.

4.5.2 系統異常狀態評估

由4.5.1 節的實驗過程得到測試集中各關鍵特征參數的異常度量值、各測試集的系統耦合度和相應的關鍵特征參數權重，由公式（13）計算各測試集的系統關鍵特征參數異常狀態值.在系統異常狀態評估階段，使用線性加權和方法、TOPSIS 方法和本文方法計算得到系統的異常狀態結果，如圖10所示.

由圖10 可見，在測試集4、5 和7 中，與線性加權和方法和TOPSIS 方法得到的異常狀態值相比，本文方法得到的異常狀態值差異較為明顯.同時由圖8可見，在測試集4、5 和7 中，多個特征參數的異常度量值較高，且不同特征參數的異常度量值之間差異較大.同時由圖9 可見，與其他測試集的系統耦合度值相比，測試集4、5 和7 的系統耦合度值較小，在系統特征參數異常度量值的線性加權和一定的條件下，耦合度值越小的測試集，其系統異常狀態值越大.因此，與其他方法計算得到的異常狀態值相比，本文方法計算得到的測試集4、5 和7 的異常狀態值差異較為明顯.

圖10 實驗結果對比圖Fig.10 Comparison of experimental results

同樣地，在測試集3、6和10中，與線性加權和方法和TOPSIS 方法得到的異常狀態值相比，本文方法得到的異常狀態值差異較小.同時由圖8 可見，在測試集3、6 和10 中，其總體特征參數的異常度量值較低，且不同特征參數的異常度量值之間差異較小.同時由圖9 可見，與其他測試集的系統耦合度值相比，測試集3、6 和10 的系統耦合度值較大，在系統特征參數異常度量值的線性加權和一定的條件下，耦合度越大的測試集，其系統異常狀態值越接近特征參數異常度量值的線性加權和.因此，與其他方法計算得到的異常狀態值相比，本文方法計算得到的測試集3、6和10的異常狀態值差異較小.

上述結果的原因在于，本文方法在計算系統異常狀態值時考慮了系統耦合度因素.由于耦合度能夠反映系統各關鍵特征參數異常度量值間的差異，但不能反映系統異常狀態值大小，因此本文方法在計算系統異常狀態值時，在線性加權和的基礎上融入耦合度因素，即在計算系統異常狀態值時能夠關注不同關鍵特征參數異常度量值之間的差異，故本文方法得到的結果更為合理.

5 結論

針對現有軟件系統異常狀態評估方法過度依賴數據標注、對時序數據的時間依賴性關注較低和系統異常狀態難以量化等問題，本文提出一種基于混合生成網絡的軟件系統異常狀態評估方法.首先，針對異常檢測方法過度依賴數據標注和對時序數據的時間依賴性關注較低等問題，設計一種基于LSTMVAE 混合生成網絡的異常檢測模型，解決異常檢測模型應用場景受限和準確率較低的問題.然后，利用LSTM-VAE 異常檢測模型對系統關鍵特征參數進行檢測并對其異常度量值進行計算，為后續系統異常狀態評估提供可靠的數據支撐.最后，通過加權耦合度優化方法計算系統異常狀態值，解決傳統軟件系統狀態評估方法難以對系統異常狀態進行量化的問題.實驗結果表明，本文方法對系統異常時序數據的時間特征更為敏感，評估結果也更為合理、有效.

由于本文在系統關鍵特征參數權重賦值過程中存在一定的主觀因素，可能導致軟件系統異常狀態的評估結果隨評估主體的不同而改變，下一步將重點研究采用主客觀相互結合［19］的賦權方法以減少主觀因素對軟件系統異常狀態評估的影響.