鋼筋非均勻銹蝕導致混凝土開裂的研究

劉繼睿，商懷帥，王瑋釗，李樹良，胡忠存

(青島理工大學 土木工程學院，青島266525)

鋼筋混凝土內部鋼筋銹蝕產物體積是原銹蝕鋼筋的2～4倍[1]。銹蝕產物體積膨脹將導致混凝土保護層開裂，裂縫的存在加速有害物質對鋼筋的侵蝕，進一步促使銹蝕的產生。銹蝕產物及保護層裂縫對鋼筋及混凝土間黏結性也將產生不利的影響，破壞鋼筋與混凝土協同工作的前提。鋼筋銹蝕導致保護層開裂是影響鋼筋混凝土結構耐久性及承載力的重要因素。因此確定混凝土保護層開裂時的鋼筋銹蝕程度及開裂后鋼筋銹蝕程度與保護層裂縫寬度之間的關系尤為重要。

對于鋼筋銹蝕導致混凝土開裂的研究已有很多，這些研究可以劃分為3個類型：試驗、解析、模擬。在試驗研究中大多采用通電加速銹蝕來到達縮短試驗時間的目的，ALONSO等[2]通過試驗研究了混凝土保護層裂縫寬度與鋼筋銹蝕深度之間的關系，并建立兩者之間的線性函數；KIM等[3]通過試驗分析銹脹裂縫的開展；NABI等[4]通過試驗對銹蝕開裂時間做出研究。理論解析層面上為簡化計算，大多采用均勻銹蝕模型，CHERNIN等[5]將保護層簡化為厚壁圓筒提出均勻銹蝕下開裂預測模型；ZHANG等[6]建立了初始缺陷下的銹蝕開裂模型。數值模擬上多采用有限元方式計算銹蝕開裂，DU等[7]通過有限元模擬分析銹蝕開裂及裂紋的發展；SANZ等[8]建立膨脹連接單元來對銹蝕產物的體積膨脹進行模擬；涂熙等[9]通過格構式模型對銹脹力引起的混凝土開裂進行模擬。

但之前的研究大多是基于鋼筋橫斷面上的銹蝕是均勻的前提下進行的，未考慮鋼筋銹蝕的不均勻性。而在實際情況下，混凝土中的鋼筋銹蝕是非均勻的，往往是靠近保護層一側銹蝕率較高，而背離保護層一側銹蝕率較低。本文將根據銹蝕三階段模型，基于鋼筋的非均勻銹蝕，應用彈性力學理論，對銹蝕導致混凝土保護層開裂時的鋼筋銹蝕深度及開裂后的裂縫發展做出預測模型。

1 鋼筋非均勻銹蝕三階段模型

1.1 銹蝕三階段模型

鋼筋混凝土內鋼筋從脫鈍開始銹蝕到保護層開裂主要經歷3個階段[10]：①鐵銹填充混凝土孔隙階段。此階段鋼筋的銹蝕產物填充在鋼筋與混凝土交接面的混凝土孔隙中，鋼筋的銹蝕不引起內力的變化；②銹脹力發展階段。當混凝土內孔隙被銹蝕物填充滿后，進一步的鋼筋銹蝕膨脹將引起在鋼筋與混凝土交界面上的銹脹力，此階段銹蝕產物外輪廓與混凝土保護層內輪廓相接觸并保持變形一致；③混凝土保護層開裂階段。鋼筋銹蝕膨脹最終將引起混凝土保護層的開裂，開裂后將有部分鐵銹會對裂縫進行填充。

根據銹蝕三階段模型，鋼筋的銹蝕深度將由三部分構成：填充混凝土孔隙對應的銹蝕深度δ1；銹脹力發展階段對應的銹蝕深度δ2；保護層開裂后對應的銹蝕深度δ3。其中第1階段獨立于其他2個階段的計算，第2、第3階段由于混凝土保護層開裂狀態的不同而采用不同的計算模型。因此鋼筋的總銹蝕深度δmax按式(1)計算：

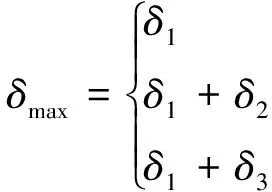
(1)

3個式子分別對應3個不同銹蝕階段的鋼筋總銹蝕深度。

1.2 孔隙填充階段δ1計算

在鐵銹填充混凝土孔隙階段，鋼筋的銹蝕深度主要取決于混凝土內部孔隙的大小和數目，這與混凝土的配合比及養護狀況有關。LIU等[10]假定在鋼筋與混凝土交界面上存在12.5 μm厚的多孔待填充區域，在銹蝕產生膨脹壓力前必須填充滿銹蝕產物。非均勻銹蝕孔隙填充模型如圖1所示，根據幾何關系可得待填充區被填滿時的銹蝕深度：

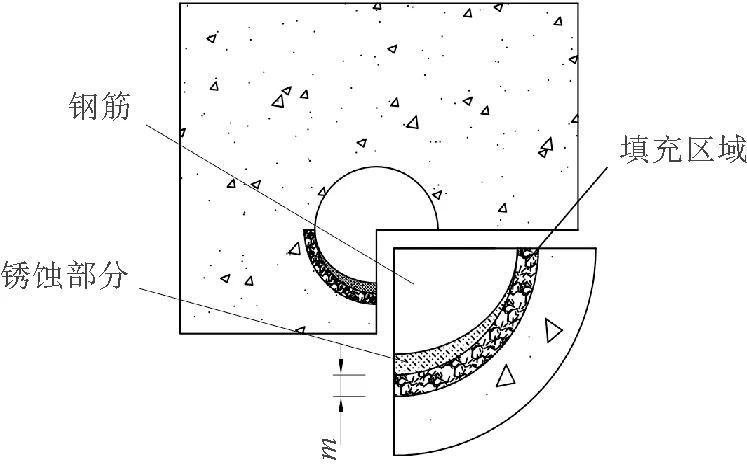
圖1 非均勻銹蝕孔隙填充模型

(2)

式中：m為填充區域厚度；n為銹蝕膨脹率；P為填充區混凝土的孔隙率，根據文獻[11]的研究取P=12%。

1.3 銹脹力發展階段δ2計算

1.3.1 鋼筋銹蝕非均勻分布特征

鋼筋銹蝕引起混凝土的開裂不僅與鋼筋的銹蝕率有關，而且與鋼筋的銹蝕分布有關。國內外的研究表明混凝土中的鋼筋銹蝕多為不均勻的。銹蝕的主要分布特征為面向保護層一側銹蝕較嚴重，而背離保護層一側的銹蝕較輕。YUAN等[12]的試驗表明混凝土銹蝕開裂前的銹蝕產物僅分布在面向混凝土保護層側鋼筋的半圓周上，且分布呈半橢圓形。ZHAO等[13]提出了模擬鋼筋銹蝕層不均勻分布的高斯函數模型。由于混凝土保護層開裂時背離保護層一側鋼筋銹蝕率很小，本文的鋼筋銹蝕模型采用假設如下：①不考慮背離保護層一側鋼筋的銹蝕；②面向保護層一側鋼筋銹蝕后輪廓為橢圓形；③銹蝕產物體積正比于被銹蝕鋼筋體積。鋼筋非均勻銹蝕形態如圖2所示。

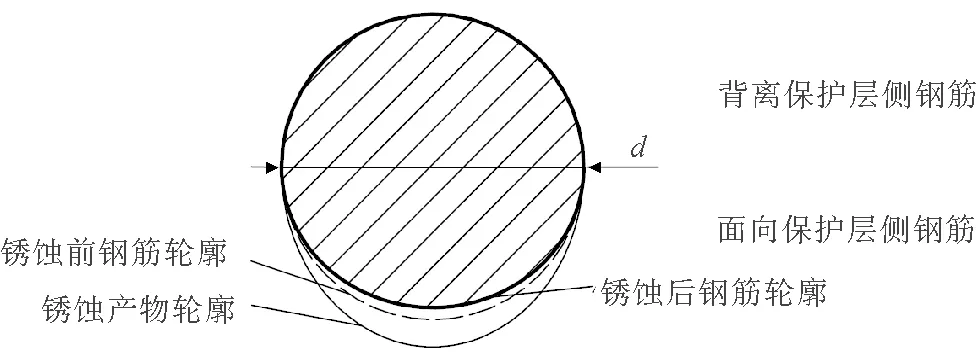
圖2 鋼筋非均勻銹蝕形態

1.3.2 非均勻銹蝕銹脹力分布模型

鋼筋銹蝕體積膨脹必將產生作用于混凝土的銹脹力。對于非均勻銹脹力的分布已有很多研究，劉榮桂等[14]假定銹脹力為橢圓形分布并分解為均勻銹脹力與偏差銹脹力疊加計算。趙羽習等[15]提出3種非均勻銹脹壓力用于反映不同的銹蝕情況。在本研究中取半圓筒狀混凝土保護層，銹脹壓力作用于面向保護層一側鋼筋與混凝土的接觸面上，根據保護層的平衡條件取均布荷載代替其他部分混凝土對保護層的約束作用。為簡化計算將保護層沿橫向展開為矩形板，銹脹壓力假定按正弦函數形態分布于展開的保護層表面。銹蝕產生的銹脹力如圖3所示。

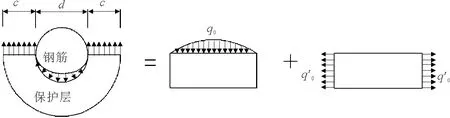
圖3 非均勻銹脹力簡化模型

建立空間直角坐標系(圖4)，作用于保護層上表面的銹脹力分布取：

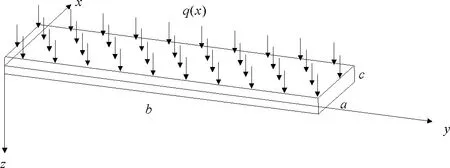
圖4 展開板計算坐標系

(3)

其中，展開寬度a=π(c+d)/2，c為保護層厚度，d為鋼筋直徑。

取展開前保護層進行受力分析，根據保護層部分的受力平衡條件計算q′0與最大銹脹力q0的關系：

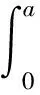
(4)

(5)

1.3.3 銹蝕膨脹力-應力關系

在銹脹力計算部分已考慮其他部分混凝土對保護層的約束作用，并將約束轉化為力的形式。故可將展開的保護層視為兩邊簡支的彈性板，其表面受到垂直于板面的銹脹力作用。由于鋼筋縱向長度遠大于鋼筋直徑及混凝土的保護層厚度，故彈性板縱向可假設為無限長。計算簡圖如圖5所示。

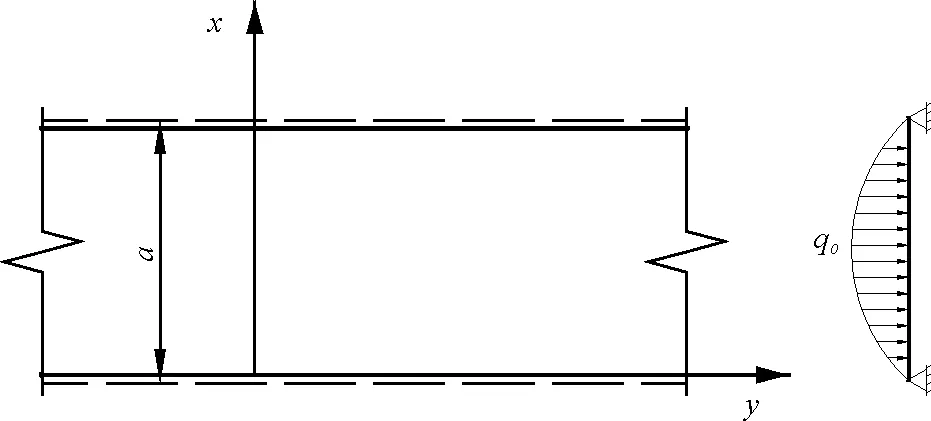
圖5 展開板約束及荷載分布

由于不考慮銹脹力沿縱長方向的不均勻性，則荷載沿y方向不發生變化，即荷載函數q0=q(x)只是關于x的函數。此時彈性板的撓度函數ω(x)也僅與x有關，所以撓度函數對y的各階導數均為0，因此彈性板的控制方程為

(6)

(7)

式中：D為彈性板的抗彎剛度；E為楊氏模量；μ為泊松比。

考慮邊界條件，在x=0，a邊界上：

(8)

對式(6)進行積分，得

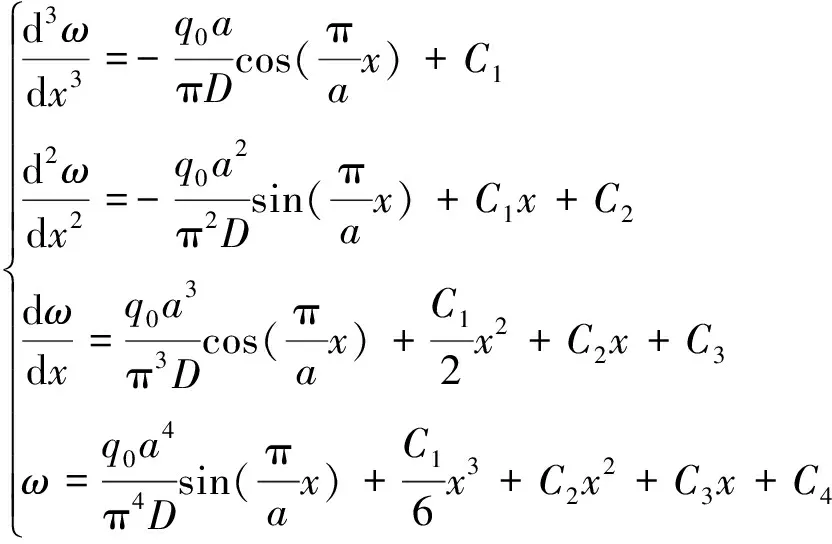
(9)

由式(8)板的邊界條件，得

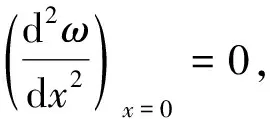
x=0時，(ω)x=0=0，得C4=0；

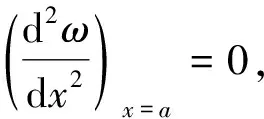
x=a時，(ω)x=a=0，得C3=0。

于是按照兩邊簡支的無限長彈性板理論計算得到撓度函數：

(10)

不考慮泊松比μ的影響，則銹脹力函數(式(3))產生的應力為

(11)

計算由q′0產生的應力：

(12)

則在彈性板中的總應力：

(13)

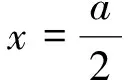
(14)

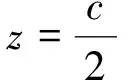
(15)

在式(15)中，當σx,max=fct時，混凝土表層會因鋼筋銹蝕膨脹而開裂，且裂紋開展方向平行于鋼筋縱長方向，其中fct為混凝土抗拉強度。此時q0為

(16)

1.3.4 銹蝕率-變形關系

基于1.3.1章節對銹蝕模型做出的假設，取最大銹蝕深度為δ2，則在橫斷面上發生銹蝕的鋼筋面積為

(17)

此時的名義銹蝕率為

(18)

由于鋼筋銹蝕產物體積膨脹，其銹蝕產物的增長量即在橫截面上面積的變化量S2為

(19)

根據前期的荷載分布假設模型，由鋼筋銹蝕膨脹邊界與混凝土保護層展開板內邊界的變形協調條件，將銹蝕產物面積增量按照總量不變的原則，以正弦分布的方式分散到展開面上，則將引起混凝土保護層的變形。根據模型假設，產生的變形發生在坐標系z方向上且沿y軸不發生變化，于是彈性板的撓度可假設為

(20)

結合式(19)可求出待定系數A，進而求出銹蝕產物膨脹產生的撓曲線方程：

(21)

(22)

(23)

1.3.5 開裂時銹蝕深度計算

由銹脹力引起的撓度方程(式(10))與銹脹產物體積變化引起的撓度方程(式(23))，根據撓度函數的唯一性，可得銹蝕膨脹力與鋼筋最大銹蝕深度的關系：

(24)

由混凝土開裂時的銹脹力(式(16))與銹脹力與最大銹蝕深度關系(式(24))可得混凝土開裂時鋼筋的最大銹蝕深度：

(25)

將混凝土開裂時的最大銹蝕深度(式(24))代入名義銹蝕率(式(18))可得由已知量表示的混凝土保護層開裂時的名義銹蝕率：

(26)

1.4 保護層開裂階段δ3計算

混凝土保護層一旦銹蝕開裂，上述彈性平板模型將不再適用。由于開裂后的混凝土保護層在中部斷開，此時要考慮其他部分混凝土對保護層的約束作用，可將開裂后的保護層展開板視為兩端底部簡支跨中分離的兩部分，并將其他部分混凝土對保護層的約束視為彈簧支座。同時考慮鐵銹對裂縫的填充，為簡化計算，由于鐵銹對裂縫的填充量較小，故可先不考慮鐵銹對裂縫的填充估算保護層外表面開裂寬度l′，再通過扣除填充部分的鐵銹對l′進行修正得到裂縫寬度l。在圖6中陰影部分的面積應等于銹蝕產物的增長量，開裂后由變形條件可得保護層中點的豎向位移ω2：

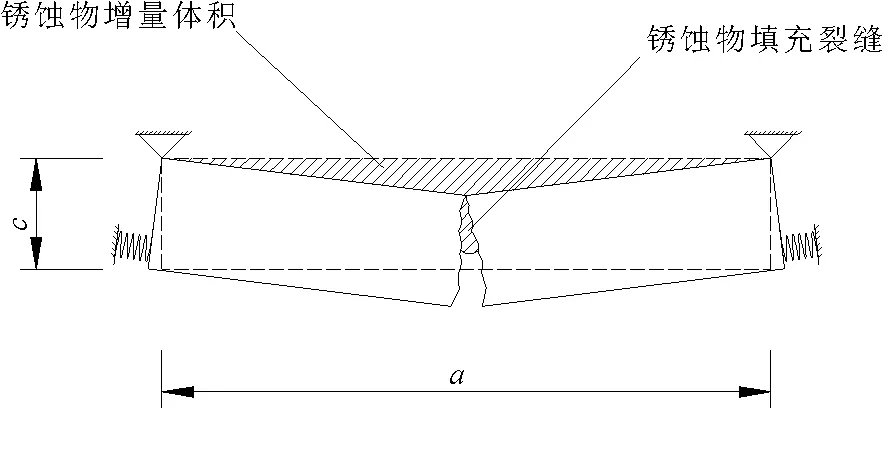
圖6 保護層開裂后計算模型

(27)

通過幾何關系可得保護層表面修正前裂縫寬度l′：

(28)

將式(27)代入式(28)，由于銹蝕引起的位移量很小，故式(28)可化簡為

(29)

考慮鐵銹對裂縫的填充對式(29)進行修正求得修正后的裂縫寬度l：

(30)

式中：λ為鐵銹對裂縫的填充率。

移項得出最大銹蝕深度與混凝土表面裂縫之間的關系式：

(31)

由于銹蝕層依然按照半橢圓假設，故銹蝕率與銹蝕深度之間的換算公式式(18)在此時依然適用。

2 試驗驗證

2.1 銹蝕開裂時的裂縫寬度

保護層在恰好開裂時刻，鋼筋的銹蝕率與恰好開裂前相同，即δ2=δ3，但開裂前后的模型假設不同。可根據開裂前的銹脹模型計算開裂時刻的名義銹蝕率，再根據此時間點的銹蝕率不變的原則，將名義銹蝕率代入銹蝕開裂后的模型，計算恰好開裂時混凝土保護層外表面的裂縫寬度。現取鋼筋直徑d=(18±5) mm，保護層厚度c=(40±5) mm，銹蝕膨脹率n=3±1，混凝土抗拉強度標準值fck=(2.0±0.5) MPa，混凝土彈性模量E=(30±2) GPa。將以上參數代入式(25)、式(26)估算開裂時的最大銹蝕深度及名義銹蝕率：

(32)

結合式(25)與式(30)可推算銹蝕開裂時刻的混凝土保護層外表面裂縫寬度：

(33)

l=3～8 μm

(34)

通過上述檢驗可以看到初始開裂時刻的最大銹蝕深度在3～18 μm。這與文獻[16]的試驗結果(保護層開裂時鋼筋銹蝕深度一般為10～20 μm)基本一致。保護層外側初始裂縫寬度在3～8 μm，由于開裂時刻的裂縫寬度較小，可觀測裂縫的最小寬度一般在50～100 μm，因此在試驗中很難及時觀察到，且已有的研究表明保護層裂縫只有發展到一定的寬度后才會對混凝土結構的耐久性及鋼筋與混凝土間的黏結力產生不利影響。因此本文將模型驗證重點置于不均勻銹蝕開裂后的保護層外表面裂縫寬度與鋼筋銹蝕程度的關系上。

2.2 開裂后的裂縫寬度

開裂后鋼筋銹蝕深度為δmax=δ1+δ3，采用文獻[17]數據對模型進行檢驗。該試驗通過全浸泡通電加速銹蝕的方法研究了保護層厚度、鋼筋直徑、混凝土強度對銹蝕開裂的影響。試驗結果發現銹脹產生的裂縫均產生在平行于鋼筋方向，這與本模型的計算結果相一致。由于該試驗是在全浸泡環境下進行的，且試驗中觀測到裂縫處有銹蝕產物滲出，故需考慮保護層開裂后部分銹蝕產物的溶出。鐵銹溶出率取15%，銹蝕膨脹率n=2.0，鐵銹裂縫填充率λ=1.0。

對試驗中每種情況的3個試件裂縫寬度及銹蝕率結果取平均值，并根據銹蝕率按式(18)反推鋼筋的銹蝕深度。試驗及模型計算結果見表1及圖7。

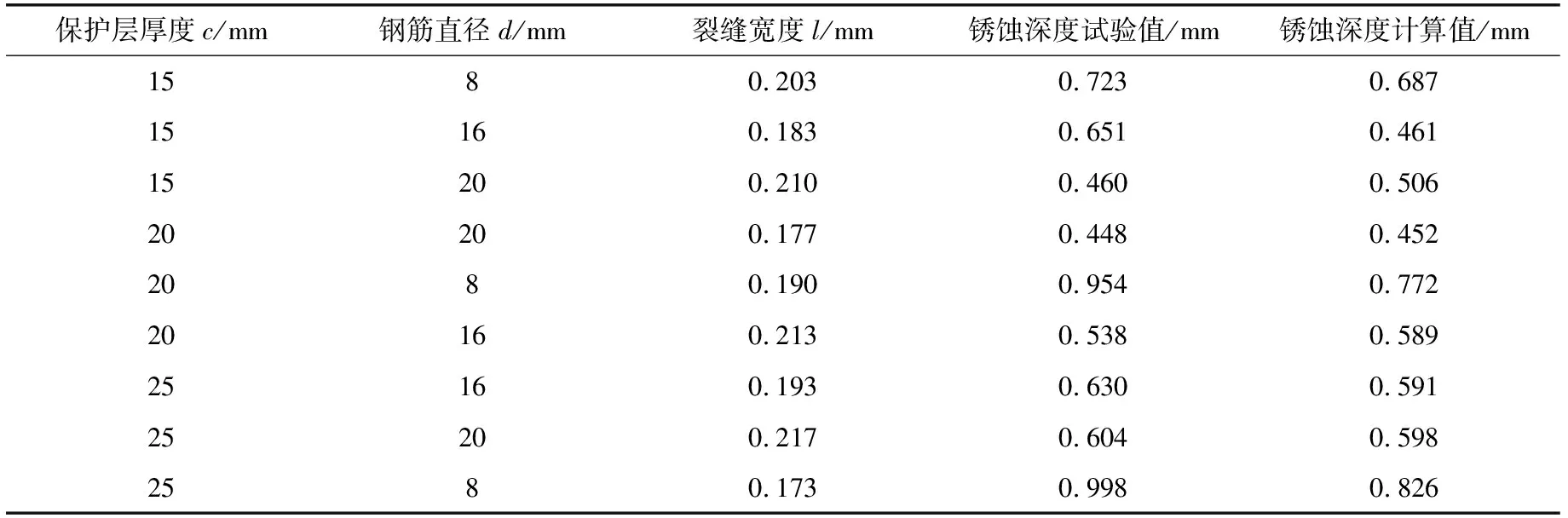
表1 保護層裂縫寬度與鋼筋銹蝕深度

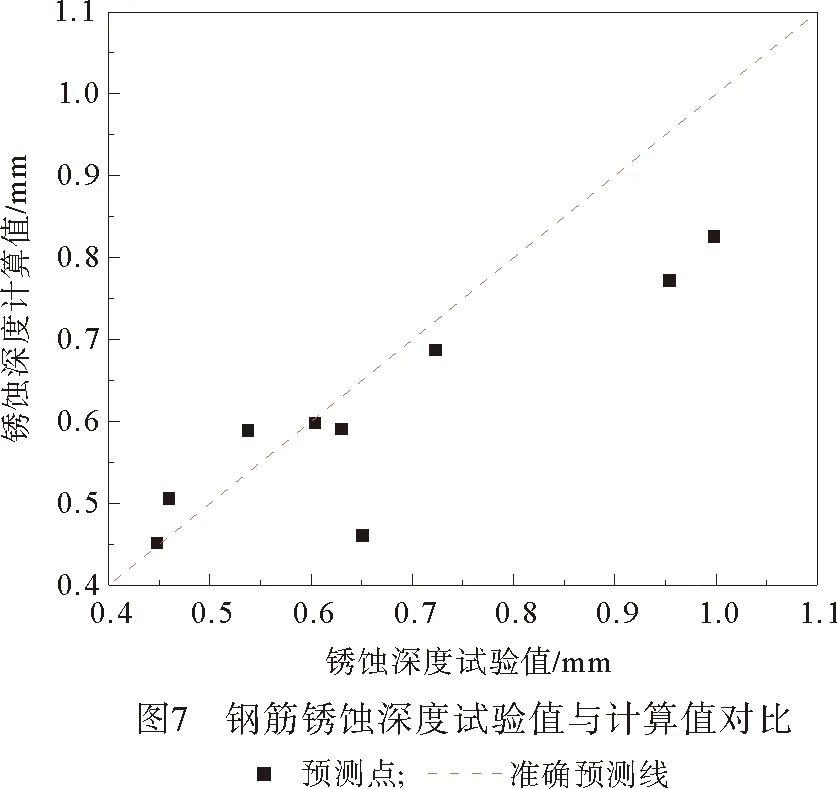
從圖7可以看出公式推導結果與試驗數據基本一致，兩者的相關系數為0.90，非均勻銹蝕模型可以在一定程度上對銹蝕開裂狀況做出預測。但是對于銹蝕深度較大的鋼筋預測值偏低，分析原因主要是銹蝕程度增大，產生的銹蝕物填滿裂縫后將產生更多的溶出，消散部分銹脹力，而預測模型未考慮鐵銹溶出率的變化。其次鐵銹在裂縫的填充過程中也將對裂縫路徑邊緣的混凝土孔隙進行填充，由于實際情況下裂縫路徑復雜，該部分銹蝕填充量難以計算。

3 結論

1) 在非均勻銹蝕模型中應用傳統的銹蝕三階段理論，使用不同的模型對不同銹蝕階段的鋼筋進行計算，使分析明確，結果可靠。

2) 采用彈性板理論，通過非均勻銹蝕模型對銹蝕第2階段與第3階段的交接點，即保護層開裂時刻的鋼筋銹蝕深度及保護層表面裂縫寬度進行估算，并與試驗結果對比，發現該計算模型可以較準確地估計混凝土開裂時刻的銹蝕深度，也發現此時保護層裂縫寬度較小，在試驗中很難加以觀測。

3) 對第3階段的銹蝕開裂狀況進行計算，建立非均勻銹蝕條件下的鋼筋銹蝕最大深度與保護層外表面裂縫寬度之間的關系。通過試驗數據對計算結果進行驗證，發現該非均勻銹蝕模型與試驗結果較為符合，但對于高銹蝕程度鋼筋銹蝕深度預測偏低，有待進一步研究。