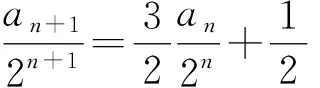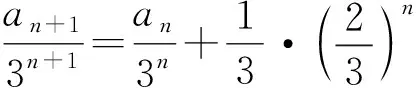讓數學教學自然生成
福建省長汀一中 (366300) 付禮福
許多學生到高中后就感到數學更難學,更加抽象,知識更嚴謹,更加深奧難懂.數學給人以冷冰冰的、枯燥無味的感覺.事實上,高中數學是思維的科學,只有鉆進去了才能感受到它是冰冷的美麗.它有簡單美、對稱美、曲線美、和諧美、自然美.數學教學中,教師應展示數學自然、精彩、美麗的本來面目,讓數學來得更自然一些.只有在符合認知規律的自然生態下,學生的素養才能得到有效發展.
一、知識的產生要自然
數學來源于生活實際,又應用于生活.數學知識的產生和發展都是自然的與合理的.完美的數學符號、概念、法則、定理,是數學界長期自然、合理進化的結果.
學習的目的是運用、創新,建立知識結構框架,是學好高中數學的關鍵.數學概念、公式、法則是學好數學,解決數學問題的前提和基礎.自然合理的才容易讓人接受、理解,強塞硬灌的東西會被排斥.教學時,要注重概念的形成過程,公式的推導過程,讓學生明確學習的必要性和意義,并且要抓住知識間的內在聯系,讓抽象知識直觀化、具體化,自然而然地生成.
比如,函數的單調性是函數概念之后學習的第一個重要性質,是函數學習中第一個用數學符號語言刻畫的概念.這種由形到數的翻譯,從直觀到抽象的轉變,對高一學生來說是難點.我通過提出下列問題,讓學生思考,體驗函數單調性概念的自然生成.
問題1 怎樣用數學符號語言刻畫“y隨x的增大而增大”,“y隨x的增大而減小”這個特征?
答:當x1
問題2 為什么要在給定區間內取兩個數x1、x2?
答:體現數的增大,至少要兩個值,設為x1、x2,且x1 問題3 在給定區間內僅取兩個數x1、x2能足夠說明“x增大,y也隨之增大” 這個特征嗎? 答:舉一反例y=x2,取x1=-1,x2=2,由x1 學生通過足夠的時間思考、辨析,舉反例等,對概念本質的理解更加深入,函數的單調性概念基本成型.乘勢追問: 問題4 如果在給定的某個區間內,函數的圖象從左到右一直是上升的,我們就說該函數在這個區間內是增函數.你能否敘述單調增函數的定義? 至此,函數的單調性概念算是水到渠成了,再通過應用加以鞏固、深化和提高.再如人教A版(2019)三角函數一章,三角函數的圖象和性質與函數y=Asin(ωx+φ)的圖象,之間隔了一個三角恒等變換,這給圖象學習帶來不便,不自然,應調整順序. 思維的產生源于問題,對問題進行觀察、分析、綜合、判斷、推理等認識活動過程就是思維,是一種習慣性的思考方式.思維要靈活、嚴密、完整、有序,思維過程要自然,合情合理,不能詭異、突然的,大跨度的跳躍會讓人莫名奇妙,就象變魔術,無法接受和理解.解決問題的一般思維程序是“審題→聯想→嘗試→反思”,明確目標,“由已知想可知”的正向推理,或“由未知想需知”的逆向思考,或“兩面夾攻”,不斷嘗試,調整思路,直至思維貫通.若思路不通或麻煩,則可嘗試把問題等價轉化,換一種形式再思考.如AB中點為M,AB=2OM,意即OA⊥OB. 教學中,必須暴露“怎么想,為什么會這樣想的”,思維自然形成的過程,包括嘗試、碰壁、再嘗試的過程,引導學生思考探索,啟發思維.老師的包辦代替會扼殺學生思維,強塞硬灌只會增加學生思維惰性.要讓學生有饑餓感,迫切感,如饑似渴的學習.讓學生限時訓練,增強緊迫感,思維才會有效果.課堂教學的過程要精心“預設”,更要關注動態“生成”.適時引導、點撥、追問、解惑.課堂上要注意師生、生生的交流互動,互教互學,互相啟發,讓思維碰撞,迸發出智慧的火花,從而“站在巨人肩膀上攀登”,實現合作共贏,共同發展. 圖1 圖2 例2 (2021新高考全國Ⅰ卷)如圖2,在三棱錐A-BCD中,平面ABD⊥平面BCD,AB=AD,O為BD的中點. (1)證明:AO⊥CD; (2)若△OCD是邊長為1的等邊三角形,點E在棱AD上,DE=2EA,且二面角E-BC-D的大小為45°,求三棱錐A-BCD的體積. 分析:(1)逆向思考方便,要證線線垂直,只需證線面垂直,那么證哪條線與哪個平面垂直好呢?觀察圖形,結合已知,易知應去證AO⊥平面BCD,轉化為只要證AO垂直于兩個垂直平面的交線BD,而這易得,從而問題得證. 圖3 教師的作用是啟思導學,“授人以漁”,進行激勵、喚醒、引領.學習數學離不開解題,解題的目的是鞏固和加深對數學知識的理解,提高思維能力.在解決問題過程中,要引導學生多角度、多方位、多層次的思考,尋找解決的線索或路徑,并注意整理思路,使“條理清楚,邏輯嚴密,步步有據,思路清晰,規范簡潔”. 教學是師生的共同活動,“教學做合一”,教學生學,在做中教,在做中學,在做中感悟.“做”是核心,在做中融會貫通,靈活運用.解題思路要自然而然地展開,把復雜的東西簡單化,難理解的東西通俗化,弄懂“為什么這樣想”,找到更適合學生的自然解法,從而實現模仿到創新. 例3 (2016全國Ⅰ卷理)已知函數f(x)=(x-2)ex+a(x-1)2有兩個零點. (1)求a的取值范圍;(2)設x1,x2是f(x)的兩個零點,證明:x1+x2<2. (1)解法1:(對參數分類討論)f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a). (i)設a=0,則f(x)=(x-2)ex,f(x)只有一個零點x=2,不符合題意. (ii)設a>0,則當x∈(-∞,1)時,f′(x)<0;當x∈(1,+∞)時,f′(x)>0.所以f(x)在(-∞,1)單調遞減,在(1,+∞)單調遞增.又f(1)=-e<0,f(2)=a>0,當x→-∞時,f(x)→+∞,此時f(x)存在兩個零點,符合題意. 圖4 (2)證法1:由解法1知f(x)在(-∞,1)單調遞減,在(1,+∞)單調遞增,由(1)結果不妨設x1<1 教學不僅是傳授學生知識,更重要的是培養學生的思維能力,進行思想引領.在課堂教學中,應抓住思維訓練這條主線,進行變式教學,通過問題驅動,激發學生去思考、創新.變式就是改變問題的條件或結論,變換問題的形式或內容,一般化或特殊化,得到新問題,激勵學生進行重新思考,會從“變”的現象中發現“不變”的本質或規律,加深對知識的理解,培養學生的應變能力,切實從題海中走出來,實現真正的減負與增效. 變式要有針對性,要適度讓學生參與.可以通過一些過渡性的語言,比如“還能求什么呢”“如果把這些條件稍微改一下,還能得到這個結果嗎”,變式自然地生成,讓學生清楚的認識到教師是怎樣進行變式的,培養思維的靈活性、發散性,提高思維能力. 例4 已知數列{an}中,a1=1,且an+1=an+2n,求數列{an}的通項an. 目的是讓學生掌握累加法求數列的通項,條件改為下面時呢? 變式1 已知數列{an}中,a1=1,且an+1=an+2,求數列{an}的通項an. 就是用公式法求數列的通項,條件改為下面時呢? 變式2 已知數列{an}中,a1=1,且an+1=3an+2,求數列{an}的通項an. 就是要會用構造法求數列的通項,條件改為下面時呢? 變式3 已知數列{an}中,a1=1,且an+1=3an+2n,求數列{an}的通項an. 這也是用構造法求通項,還有別的方法嗎? 法3:已知兩邊同加2n+1,變為an+1+2n+1=3(an+2n)形式,化為等比數列,再做. 總之數學教學應抓住一切機會和環節,努力創造更自然、更合理、更有效的數學教學,確實提高學生思維的主動性、深刻性和流暢性.在教學過程中,不失時機地滲透思想教育,使學生在學習時有勇于嘗試探索,敢拼敢闖的精神;懂得取其精華,去其糟粕,批判地繼承;會辯證地分析問題,不唯師,不唯書,不迷信盲從,學會理性思維,靈活創新運用所學.二、思維過程要自然
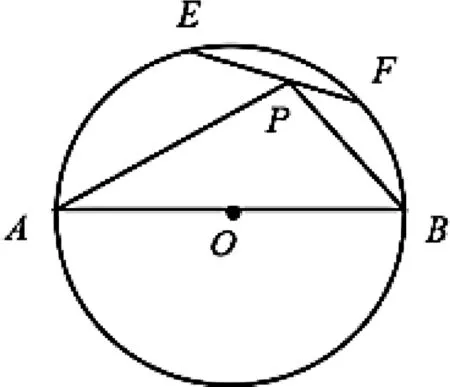

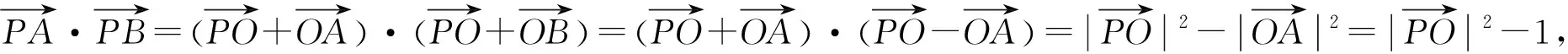

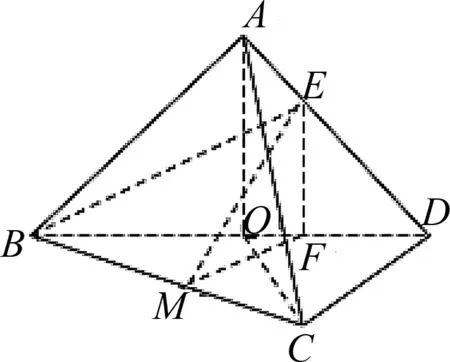
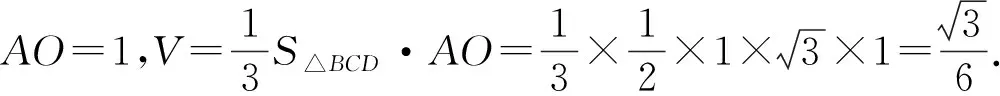
三、解法思路要自然

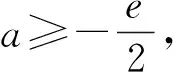
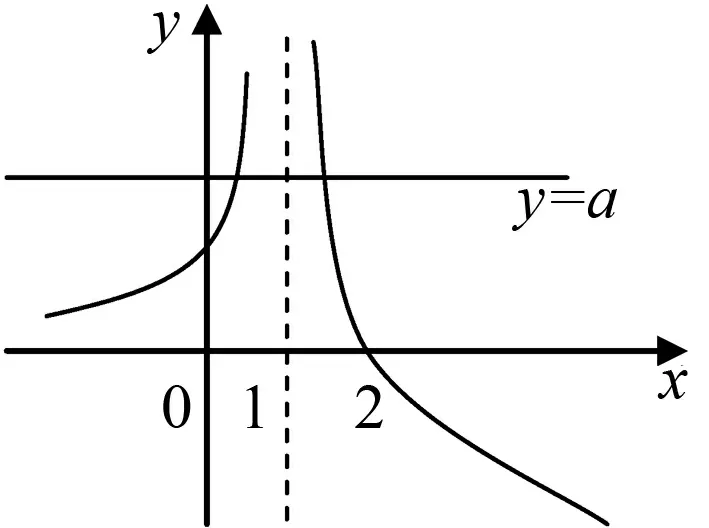

四、問題變式要自然