直觀感知 大膽猜想 小心求證
——以幾道高考數列題求解為例

閩南師范大學附屬中學(漳州二中) (363000) 黃其芳

數列作為高中數學的一個重要組成部分，是歷屆高考試題考查的重點，難點．數列的表示通常有圖象法、列舉法、通項公式、遞推關系．高考數列試題中，數列的表示往往以抽象的形式出現(一般給出其遞推關系)，為此需要將其直觀化，通過遞推關系及首項，列舉出數列各項的取值，從而猜想其通項公式，或把數列的各項用圖形給予表達，進而確立解題的思路．下面通過幾道高考數列試題加以說明．

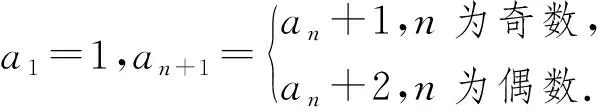
(1)記bn=a2n，寫出b1，b2，并求數列{bn}的通項公式；(2)求{an}的前20項和．

分析與解：(1)由題目中給出數列{an}的遞推公式可知，數列{an}中的偶數項是等于其前一項加1，奇數項是等于其前一項加2其首項為1，又a1=1，為此我們列舉數列的前幾項，直觀感知數列各項的值，a1=1，a2=2，a3=4，a4=5，a5=7，a6=8，…．所以b1=2，b2=5，b3=8，猜想數列{bn}是首項為2，公差為3的等差數列， 因為bn+1-bn=a2n+2-a2n=a2n+1+1-a2n=a2n+2+1-a2n=3，所以猜想成立，則bn=3n-1．

(2)同(1)，設cn=a2n-1，又c1=1，c2=4，c3=7，猜想數列{cn}是首項為1，公差為3的等差數列， 因為cn+1-cn=a2n+1-a2n-1=a2n+2-a2n-1=a2n-1+1+2-a2n-1=3，所以猜想成立，則cn=3n-2．所以{an}的前20項和為a1+a2+…+a19+a20=(c1+c2+…+c10)+(b1+b2+…+b10)=5(1+28)+5(2+29)=300．

例2 (2021年八省聯考第17題)已知各項都為正數的數列滿足an+2=2an+1+3an．

(1)證明：數列{an+an+1}為等比數列；

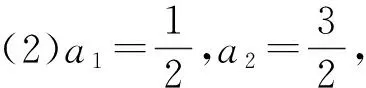
例3 (2020年全國I卷文第16題)數列{an}滿足an+2+(-1)nan=3n-1，前16項和為540，則a1=．

分析與解：題中遞推關系式關系不明顯，為此我們先列舉幾項觀察規律．由已知a3-a1=2，a4+a2=5，a5-a3=8，a6+a4=11，a7-a5=14，a8+a6=17，a9-a7=20，a10+a8=23，a11-a9=26，a12+a10=29，… ，則發現a4+a2=5，a8+a6=17，a12+a10=29，a16+a14=41，又a3=a1+2，a5=a1+2+8，a7=a1+2+8+14，a15=a1+2+8+…+38，所以a1+a3+…+a15=8a1+2·7+8·6+14·5+20·4+26·3+32·2+38·1=8a1+392，所以S16=a1+a2+…+a16=(a1+a3+…+a15)+(a2+a4+…+a16)=8a1+484=540，所以a1=7．

例4 (2014年新課標Ⅰ卷理第17題)已知數列{an}的前n項和為Sn，a1=1，an≠0，anan+1=λSn-1，其中λ為常數．

(1)證明：an+2-an=λ；(2)是否存在λ，使得{an}為等差數列？并說明理由．

分析與解：(1)略；(2)由(1)及已知條件得出數列各項為，1，λ-1，λ+1，2λ-1，…，若{an}為等差數列，則2(λ-1)=1+λ+1，解得λ=4；當λ=4時，數列各項為1，3，5，7，…，猜想{an}為等差數列，且公差為2．下面用數學歸納法證明：當λ=4時，an+1-an=2，n∈N*；當λ=4時， ①a2-a1=3-1=2，所以n=1時等式成立；②假設ak+1-ak=2，?k∈N*，則由(1)及假設得ak+2-ak+1=ak+4-ak+1=4-2=2，所以n=k+1時，等式也成立.由①②可知該等式成立．

例5(2014年高考全國Ⅱ卷理第17題)已知數列{an}滿足a1=1，an+1=3an+1．

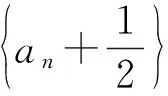
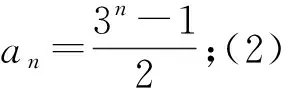
(1)若x≥0時，f(x)≤0，求λ的最小值；

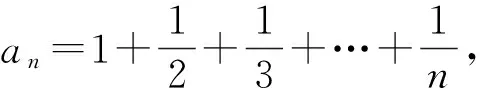
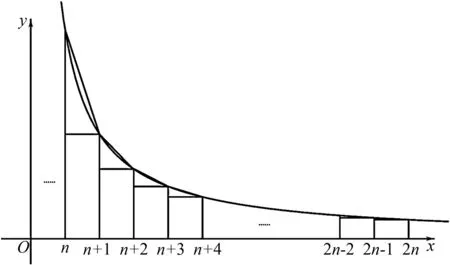
圖1

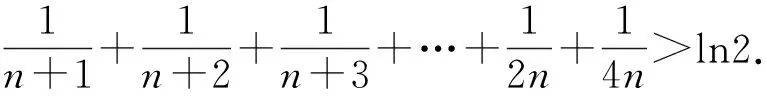
由上面幾道數列試題的解題過程，我們可以看出，若能將數列的項具體化、直觀化，則能幫助我們從不同視角理解題意，明確這道題的解題方向，因為解題思路的產生更多的源于直覺，源于我們對這道題目的直觀判斷，除非它是常規的題型，預期這道題的最終結果．直覺意義往往可以超越邏輯步驟，捷足先登的直達目標，但具體到解答步驟，還是要回到數學的抽象表達，運用嚴密的數學推理．