基于改進遺傳算法的計算機數學模型構建研究

何慶　鐘維堅　田風　林鋒　唐蘇東

【摘要】? ? 面向網絡計算機中海量的數據信息，采取傳統匹配搜索遺傳算法進行匹配點、非匹配點的遍歷，通常遍歷到無效度更高的非匹配點較多，很難在短時間內找到與樣本相近的最佳匹配點。基于此，針對基本遺傳算法的無效遍歷、數據冗余弊端，結合最小二乘法、Bagging集成聚類算法對原有遺傳算法作出改進，建立起相似度匹配的計算機數學模型，確定高精度因子匹配的參數估算范圍和辨識度，改進遺傳算法關聯矩陣編碼、解碼、交叉等集成學習與迭代環節，以擴展樣本匹配的搜索空間與深度。

【關鍵詞】? ? 改進遺傳算法? ? 計算機? ? 數學模型? ? 構建

引言：

在企業工業化生產、計算機視覺處理數據匹配中，通常需要根據視覺數據因子、工作站的數量，設置n個樣本數據為初始聚類中心，對多個相似對象進行最小誤差求解，將不同對象分配至距離其最近的聚類中心，來完成算法最優解的搜索與匹配。因而面對傳統遺傳算法具有的無效遍歷更多、搜索深度不足等特征，本文提出基于Bagging集成聚類的改進遺傳算法，建立起企業裝配線的計算機平衡優化數學模型，將雙目裝配線中的生產作業要素因子，合理分配到相應的工作站之中，進行種群聚類分析的編碼、適應度計算，得到每個個體的搜索與聚類結果。

一、傳統遺傳算法的編碼、數據搜索與交叉操作執行流程

傳統遺傳算法為美國密歇根大學J.? H.Holland教授，根據達爾文“自然選擇理論”提出的自適應數據信息搜索/優化技術，其初始群體編碼是由二進制“0”和“1”字符組成的一連串字符串，將具有類似特征的字符串組合為特定子集，并利用隨機搜索技術對多個字符串組成集合，進行交叉、變異等的迭代遺傳操作，來確定全局最優解。

因而該遺傳算法主要是對編碼后的控制參數，作出編碼串模式階次的群體矢量搜索。在完成某一空間數據參量的編碼后，先對群體P（t）展開選擇、交叉、變異等遺傳算法運算，再根據所求問題的目標函數（適應度函數），進行編碼字符串集群中個體的適應度評估，得到下一代群體P（t+1）。傳統遺傳算法的編碼、數據搜索與交叉操作的簡單執行流程如下所示。

開始程序;

t←0;

初始化種群P（t） 編碼;

評價種群P（t）編碼;

如果不符合終止條件，則開始循環;

T←t+1;

從上一代種群P（t-1）中選擇個體，形成新的群體P（t）;

種群P（T）通過交叉和變異進化;

種群P（T）的適應度計算;

評價組P（T）;

周期結束;

程序執行結束。

二、基于Bagging集成聚類的改進遺傳算法

傳統遺傳算法在多個編碼數據集群的搜索、交叉操作過程中，常常表現出無效遍歷、數據冗余、搜索深度不足等問題，因而提出Bagging集成聚類算法，利用多個基學習器進行編碼樣本的綜合學習，使聚類所有樣本到聚類中心距離的平方和最小，由此得出每個集群個體的所屬類別。

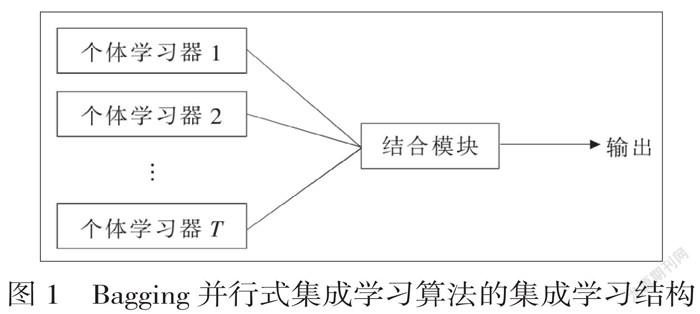
（一）Bagging并行式集成學習算法

Bagging是在統計學習采樣技術的基礎上，對多種不確定性樣本進行統計、推斷與學習的技術，具有多次抽樣、并行集成的樣本采集特征。如先給定樣本容量為n的編碼數據集群，從該集群中隨機取出某一樣本，放入Bagging采樣數據集，再將該樣本放回初始數據集，經過這樣多次的隨機抽樣，重復抽樣的過程為T次，得到涵蓋v個樣本的采樣數據集，可記為Bagging樣本Di=（x1，x2，…，xv），i=1，2，…，T。

針對以上T個采樣出的訓練樣本集，選取多個基學習器對每個采樣集的v個樣本進行訓練，再將以上多個基學習器的訓練結果作出整合，輸出為最終的Bagging并行式集成學習結果，完成Bagging算法的基本執行流程，具體集成學習結構如圖1所示：

（二）Bagging與K均值聚類結合的遺傳算法

集成聚類的遺傳學習算法，是將Bagging集成學習算法、K均值聚類算法進行結合，生成K均值集成聚類算法，選定多個基學習器進行樣本的訓練學習，該機器訓練學習流程屬于無監督學習。也就是通常使用無標簽的數據集、聚類準則函數，構建起用于聚類分析的準則函數：

（1）

具體集成聚類遺傳算法的執行流程如圖2所示。

第一步，給出n個混合樣本，選取K個初始聚合中心Zj（I），j=1，2，...，K，其中I表示迭代次數。

第二步，利用Bagging集成學習算法采樣數據訓練集，將原始數據集的隨機抽樣放回原處，重復抽樣過程T-1次，并獲得涵蓋v個樣本的總共T-1抽樣數據集，表示為Di=（x1，x2，…，xv），i=1，2，…，T-1。

第三步，在完成多個樣本歸類時，取出未抽樣的w個樣本，形成另一個取樣集，記錄為DT=（x1，x2，…，xv），則可以將以上的樣本采樣數據集總和為：

（2）

第四步，使用多個K均值基學習器，在T樣本集上執行單獨的聚類訓練。將初始聚類類別數設置為K，將初始訓練集中的樣本數設置為z，建立K·z相關矩陣，并由基礎學習者對樣本進行聚類。記錄基學習器的不同樣本聚類類別投票的數據信息，如第i行和第j列的s數值，則表明存在有s個均值基學習器，對第i樣本歸類為第j類。

第五步，根據以上的K·z維關聯矩陣，依照投票法則進行每個樣本聚類類別的表示，其中投票數最多的聚類類別為樣本類別，若投票數相同則隨機選擇某一類別，作為樣本最終的聚類類別。

第六步，計算不同樣本到聚合中心的距離D （xk，Zj（I））min={D（xk，Zj（I）），其中k=1 ，2，…，n，j=1，2，...，K，且xk∈wi。之后將得到的k個新的聚合中心，用

進行表示。

第七步，判斷Zj（I+1）、Zj（I）之間的關系，若Zj（I+1）≠Zj（I）則將I+1的值賦給I，并返回第二步，否則結束算法。

圖2? ? Bagging與K均值集成聚類遺傳算法的執行流程

三、基于改進遺傳算法的企業裝配線計算機平衡優化數學模型

在企業裝配線產線生產過程中，通常圍繞工作站數、作業元素等的約束條件下，定義了裝配線生產率和平滑因子的優化目標，建立了裝配線多目標計算機平衡優化模型。

（一）裝配流水線的作業約束

假設I為企業裝配線作業元素的集合、J為工作站集合，設置裝配線生產速率為C，m、n分別為裝配線種群的工作站數目、作業元素個數，則Jk為第k個工作站的不同作業元素集合，k∈（1，M）。

因此，可設置企業裝配線的作業元素集合為x=[x1，x2，…，xn]，將所有滿足工作站數、作業元素等的約束條件的作業元素，整合為X=M·n的關系矩陣，表示不同作業元素在裝配工作站中的分配情況，其中X（i，k）∈X。若X（i，k）=0，則表示裝配線元素i未被分配到工作站k中;若X（i，k）=1，則表示裝配線元素i被分配到工作站k之中。之后設置Ppred為裝配線作業元素i的n×n維關系矩陣集合，Ppred（i，1）表示初始作業元素，Ppred（k，i）=1表示k為i的前序作業元素，Ppred（k，i）=0表示k為i的后序作業元素。那么在企業裝配線生產作業過程中，將每個作業元素i分配至單一的工作站，需要滿足以下的優先關系條件：

不同裝配線工作站的作業元素分配、生產速率（作業總時間）等執行公式如下所示：

（二）裝配線作業的優化目標

根據企業裝配線作業生產速率C、平滑因子S等的優化目標，定義工作站作業時長的最大值為生產速率C，C=maxTk、k∈（1，M）;定義平滑因子為企業裝配線負荷利用率、人員利用率等平衡指標，平滑因子

因而依據以上約束條件下的企業裝配線作業生產速率C、平滑因子S等優化目標，可以得出企業裝配線計算機平衡優化的數學模型為：

（三）Bagging集成聚類的改進遺傳算法執行流程

為了改進與提升傳統遺傳算法，所存在的數據搜索深度、數據遍歷效率水平，主要利用Bagging集成聚類算法，對原有利用隨機搜索技術的交叉、變異等迭代遺傳操作，作出遺傳算法種群聚類、交叉分析的改進。根據企業裝配線的計算機平衡優化數學模型，將雙目裝配線中的生產作業要素因子，合理分配到相應的工作站之中，進行種群聚類分析的編碼、適應度計算，得到每個個體的搜索與聚類結果，判定隨機配對的個體是否屬于同一種群聚類，以此來確定全局最優解。

記Spop為裝配線生產速率C、平滑因子S等種群的數目;pop（t）為第t代種群、G為遺傳代數;Pc表示交叉概率、Pm表示變異概率。則Bagging集成聚類的改進遺傳算法執行流程如下所示：

第一步，設置包括Spop、G、C、S、M、Pc、Pm、T、v、K等的初始值。

第二步，令t=0，根據設置的初始化種群Ppop（0），隨機產生種群Spop的多個個體數目量。

第三步，圍繞第t代種群P（t）的多個個體，進行第t代種群適應度的計算，計算得出裝配線作業生產速率C、平滑因子S等的適應度參考值。

第四步，懲罰項。檢查每一代種群個體，是否滿足裝配線工作站數、作業元素等的約束條件。若不滿足以M固定值為主的工作站數量約束條件，則需要向多個種群個體添加相應的適應行懲罰項，例如設置適應性參考值為500的極大值，淘汰掉那些不符合適應度要求的個體。

第五步，根據作業生產速率C、平滑因子S等的適應度參考值，進行雙目標并列選擇的操作，選出具有最優適應度參考值的種群個體，將其標記為S=Spop/2，然后對多個最優個體重組為第t+1代的新種群。

第六步，利用Bagging集成聚類算法，進行交叉與變異操作。依托Bagging集成聚類算法，采用單點交叉、單點變異規則，在個體編碼字符串中設置交叉點、基因變異點，從對應基因范圍內取一數值代替原有種群個體值。

第八步，循環操作。若滿足工作站數為M的固定值約束，將t+1賦值給t，停止循環迭代計算;否則轉向第三步。

四、基于改進遺傳算法的計算機平衡優化模型的仿真實驗分析

為對改進后的bagging集成聚類算法，進行深度搜索、交叉計算能力的驗證，本文以某以制造業的變速箱裝配線作業為例，設置變速箱裝配線工作站M=12、作業元素數量n=27的優先關系，具體如下圖所示。借助于MATLAB 2019b仿真模型，對該裝配線生產速率C、平滑因子S的計算進行平衡優化，具體計算機數學模型的參量設定如下：裝配線固定工作站M=12、作業元素數量n=27，以及生產速率初始值C=130s、平滑因子種群數量S=200、交叉概率Pc=0.6、變異概率Pm=0.05、遺傳代數G=50。

當在每組實驗中分別設定參數T=5～7、v=60～80、K=3～5時（如表1所示），得到的裝配線生產速率C=120s、平滑因子S=18.3～18.4，具體優化過程如圖3所示，優化時對不同代種群的生產速率C、平滑因子S最優值進行記錄。

圖3? ? 基于Bagging改進遺傳算法的生產速率C、平滑因子S優化過程

表1? ? 仿真實驗參數設定與結果分析

仿真實驗設定參數 裝配線生產速率C/s 平滑因子S

未改進遺傳算法 130 19.71

T=5、v=60、K=3 120 18.36

T=5、v=80、K=5 120 18.27

T=7、v=60、K=5 120 18.43

T=7、v=80、K=3 120 18.41

從圖3、表1可以得出，裝配線作業生產速率的優化在5代以內得到最優值，平滑因子S分別在15代、40代后收斂，裝配生產速率C、平滑因子S的雙目標均得到優化。但由于在多次Bagging集成聚類算法的平衡優化過程中，得到的平滑因子S數值存在著變化性，因此可以認為在不同參數設置下，平滑因子S優化的搜索深度不同。從整體上看，在4次實驗中分別設定不同參數背景下，最終平滑因子S=18.3～18.4優于未改進遺傳算法的最優解，提高了裝配效率、減少了總空閑時間，該Bagging集成聚類算法可用于對可行解進行深度搜索。

參? 考? 文? 獻

[1] 余航.計算機數學建模中改進遺傳算法與最小二乘法應用[J].? 電子設計工程. 2020（01）：15-18.

[2] 陳軍紅.平面控制網的復數域最小二乘法估計研究[J].? 華中師范大學學報（自然科學版）. 2019（02）：181-188.

[3] 李鳳坤.改進AHP-GA算法的多目標配送路徑優化[J].? 計算機系統應用. 2019（02）：152-157.

[4] 丁立超，黃楓，潘偉.基于改進混沌遺傳算法的炮兵火力分配方法[J].? 系統仿真技術. 2021（01）：12-16.

[5] 鐘育彬，鄧文杰.基于復雜適應度函數的因素遺傳算法[J].? 廣州大學學報（自然科學版）. 2020（05）：47-50.

[6] 葛曉梅，李世豪.基于改進遺傳算法的多目標車間布局優化問題研究[J].? 現代制造工程. 2021（03）：10-14+9.